荷电液滴吸附细颗粒物的数值模拟分析

王军锋，谢立宇，霍元平，左子文

(江苏大学能源与动力工程学院，江苏镇江 212013)

微细颗粒物是重要的污染物来源，能较长时间漂浮于大气并易被吸入呼吸道，严重影响人类健康.目前主要采取的除尘技术，如燃煤电厂普遍安装的湿法烟气脱硫系统(WFGD)虽然对SO2和粗颗粒物的控制有一定效果，但对细颗粒物的脱除却很困难，尤其对PM2.5的捕集效率很低，且随着颗粒物粒径的减小脱除效率显著下降［1］.而国内外最新研究发现荷电的细水雾可以显著提高细颗粒物的脱除效率［2］.液滴荷电强化了液滴和颗粒间的镜像力或库仑力，使细颗粒物穿过液滴时易被液滴吸附沉降从而提升湿法烟气除尘中微细颗粒的脱除效率.该方法具有能耗低、造价低、能够去除细颗粒物和无二次污染等优点，因此在能源和环保领域具有较好的发展前景.

影响空间细颗粒物脱除效率的因素较多，不仅仅取决于液滴和细颗粒物电荷量，如气流速度，细颗粒物浓度，液滴尺寸以及液滴间的平均间距等参数的耦合作用机制尚不明确.研究这一过程的意义不仅在于提升除尘效率，也在于减少除尘的能耗.早在20世纪50年代，H.F.Kraemer等［3］就开始针对荷电液滴吸附细颗粒物这一过程展开研究，并通过试验初步证实荷电液滴对细颗粒物的吸附效率要优于非荷电液滴.近年来，不断有学者对这一过程进行理论研究，王银生等［4］采用类比法分析了这一过程，认为静电湿式除尘特别适用微细颗粒物，并且增加液滴粒度也能提高捕尘效果.周新建等［5］采用一种新的液滴表面捕集效率的计算方法，得出液滴对细颗粒物的捕集发生在整个液滴表面.对于荷电液滴吸附颗粒物的理论研究主要针对的是单液滴，而试验的研究对象多为喷雾射流或者阵列液滴，如A.Jaworek等［6］对荷电液滴吸附细颗粒物的过程进行试验，发现液滴和细颗粒物荷上相反电荷可以提高细颗粒物的脱除效率，小于1 μm的细颗粒物的脱除率可达80% ～90%，而耗水量只有50 mL·m-3.限于测量手段，试验无法具体描述荷电液滴吸附细颗粒物的详细动力学过程.为了验证理论研究的准确性，揭示荷电液滴与细颗粒物的相间作用机制，获得影响液滴吸附细颗粒的关键参数，需要通过数值计算的手段来模拟荷电液滴吸附细颗粒物的复杂多相流体动力学过程.

赵海波等［7］采用Monte Carlo技术，利用事件驱动常体积法量化了静电增强湿式除尘器的除尘过程，通过数值模拟研究得出含尘气流输运速度越大，液滴喷射速度越小，液滴尺寸越小，液滴荷质比越大越有利于可吸入颗粒物的高效脱除，但它同样针对的是群体液滴，没有给出详细的多相流体动力学演变过程.袁颖等［8］采用拉式轨道跟踪法描述了对荷电单液滴对细颗粒物的捕集过程，但模拟结果显示液滴对细颗粒物的捕集仅可能发生在液滴的正面，而根据周新建等的理论，在静电力的作用下会有一部分的细颗粒物沉积在液滴的背部.

笔者通过求解牛顿方程，获得荷电液滴周围细颗粒物的运动轨迹方程，建立一个更完整的数值模型，通过采用颗粒轨迹追踪模型(DPM)模拟荷电单液滴吸附细颗粒物的过程，在2维空间中追踪荷电和非荷电情况下细颗粒物通过液滴时的运动轨迹，获得详细的荷电液滴吸附细颗粒物的动力学演变过程，并给出沉积效率的模拟结果.

1 数学模型

1.1 理想化假设

1)如图1所示，定义当液滴形状为球体时，它的粒径为dd，荷电量为Qd.在液滴变形过程中，假设液滴始终为规则的椭球体.当We＜10时，液滴不会发生破碎.

图1 细颗粒物运动轨迹示意图

2)假设细颗粒物为球状，统一粒径为dp，荷电量为Qp，它以与气流相同的初始速度u0水平进入整个空间.计算时，当细颗粒物与液滴的粒径相差较大，可以将其看成是质点.假设细颗粒物浓度不高，忽略细颗粒物之间的碰撞，并且细颗粒物对空气流动不产生影响.

3)静电力对液滴与细颗粒物的运动均会产生影响［9］，但对液滴而言，静电力的作用相对于其他力非常微弱，因而可将其忽略.

4)细颗粒物的沉积会改变液滴的质量和荷电量，考虑到液滴的质量和荷电量远大于细颗粒物，在细颗粒物浓度不高的前提下，可以将其忽略.

5)在流场中细颗粒物的运动受黏性阻力FD，细颗粒物粒子与雾滴间的静电引力Fj，质量力Fg，Magnus力Fm，Basset力Fb，压差力FP，Saffman力Fs，粒子附加质量力Fk以及升力Fl等［10］的影响.相对于静电引力，黏性阻力以及细颗粒物自身的质量力，其他力对细颗粒物运动的影响可以忽略不计，因此在分析细颗粒物粒子在气相流场中受力时，只考虑这3个主要受力.

6)基于本研究对象中Rep均小于200，根据R.Clift等［11］的研究，液滴周围空气的流动仍属于层流，因此文中采用黏性层流模型.

1.2 液滴吸附面积比的定义

静电力的作用使大部分细颗粒物的运动轨迹发生一定的偏转，但液滴仅能捕集运动轨迹终结于液滴表面的细颗粒物，这些被液滴所捕集的细颗粒物运动轨迹被称为颗粒碰撞轨迹.单个液滴的吸附能力取决于它能吸附周围细颗粒物的范围，因此定义了1个参数来表征单个液滴的吸附能力，即液滴吸附面积比(所有颗粒碰撞轨迹所包围的截面积与液滴的截面积之比).当液滴粒径远大于颗粒物粒径时，该定义成立.如图1所示，颗粒的运动轨迹处于能被液滴捕集的极限距离，它的初始位置与x轴的纵向距离yb即为颗粒碰撞轨迹所包围的截面积的半径，液滴吸附面积比可表示为η=πyb2/［π(dd/2)2］.液滴吸附面积比越大，细颗粒物的沉积效率就越高.

1.3 颗粒的运动轨迹方程

在液滴附近的细颗粒物的运动轨迹取决于牛顿方程:

式中:m为细颗粒物的质量;up为细颗粒物的速度矢量.

式(1)中的3个力分别为单个颗粒在流场中受到的黏性阻力:

式中:Rep为细颗粒物的雷诺数;μg为空气的黏度;ug为气流的瞬时速度矢量;Cd为阻力系数;Cc为坎宁安滑移修正系数.

液滴与细颗粒物粒子均荷电时，液滴对细颗粒物的静电引力为

式中:nr为静电引力的方向单位矢量;ε0为空气的介电常数.

细颗粒物自身受到的重力为

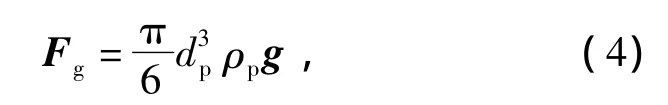
式中g为重力单位方向矢量.

坎宁汉修正因数受细颗粒物粒径影响，不同粒径对应的值可从文献［12］中查得.根据细颗粒物的初始数据计算得雷诺数，根据雷诺数可取得阻力系数Cd的值［13］:

考虑到颗粒的受力主要集中于同一个平面，因此引入笛卡尔坐标体系，取x轴为细颗粒物粒子水平运动方向，y轴为垂直地面方向，将式(2)-(4)代入式(1)得

式中:ux和uy为气流在x方向和y方向速度分量;α为细颗粒物与液滴质心的连线与x轴的夹角.

为了方便计算，引入量纲一参数.定义特征长度为液滴直径dd，特征速度为初始风速u0，特征时间为u0/dd.将式(6)，(7)量纲归一得

式中:X和Y分别为细颗粒物在x和y轴的坐标与dd之比.

其中定义了3个量纲一参数斯托克斯数Stk、库仑数Kc和G，分别为

Stk表征惯性沉积的作用，Kc表征静电力作用的大小，而G表征重力的作用.从式(8)，(9)可以看出:当给定细颗粒物初始位置，细颗粒物的运动轨迹主要由几个量纲一参数决定，即Stk，Kc，G和Rep，随着细颗粒物的运动，Rep是不断变化的，而重力对细颗粒物自身的影响相对较小，因此主要细颗粒物的运动轨迹主要取决于Stk和Kc.

2 数值模拟结果分析

2.1 细颗粒物的运动轨迹

Stk和Kc均与液滴和细颗粒物的粒径以及初始气液相对速度u0有关，改变细颗粒物粒径，液滴粒径以及初始气液相对速度，可以使这2个量纲一参数发生变化.Stk和Red不能单独更改，可以通过以下公式关联:

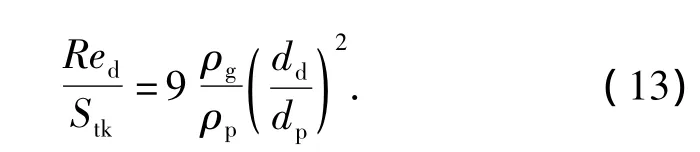
从式(13)中可以看出:Red和Stk的比例与气流速度、黏度无关，Stk给定时，细颗粒物与气体密度之比和横截面比率能决定雷诺数的大小，这个比例取决于液滴和细颗粒物粒径之比，可达1至几千.根据荷电湿式除尘的特性，取dd/dp=10.液滴周围的空气流线图如图2所示，rd为液滴半径.

由图2可以看出:气流通过液滴时，在液滴周围发生绕流.液滴和细颗粒物均不荷电(Kc=0)以及均荷电(Kc=1)时液滴周围细颗粒物的运动轨迹示意图如图3所示.在细颗粒物和液滴均不荷电的情况下，当Stk较小时(Stk=0.198)，细颗粒物的运动轨迹几乎沿着气流的流线方向，这是由于细颗粒物粒径较小，弛豫时间较短，细颗粒物粒子对于气流有良好的跟随性.在这种情况下，几乎不存在颗粒碰撞轨迹，大部分细颗粒物颗粒都随着气流逃逸了.随着Stk的提升，细颗粒物粒子的跟随性随之变差，颗粒碰撞轨迹也逐渐增多.当Stk较大(Stk=12.640)时，细颗粒物的跟随性达到较低的水平，致使细颗粒物的运动轨迹几乎呈线性，有一部分细颗粒物撞向液滴的正面发生沉积.

图2 液滴周围空气流线图

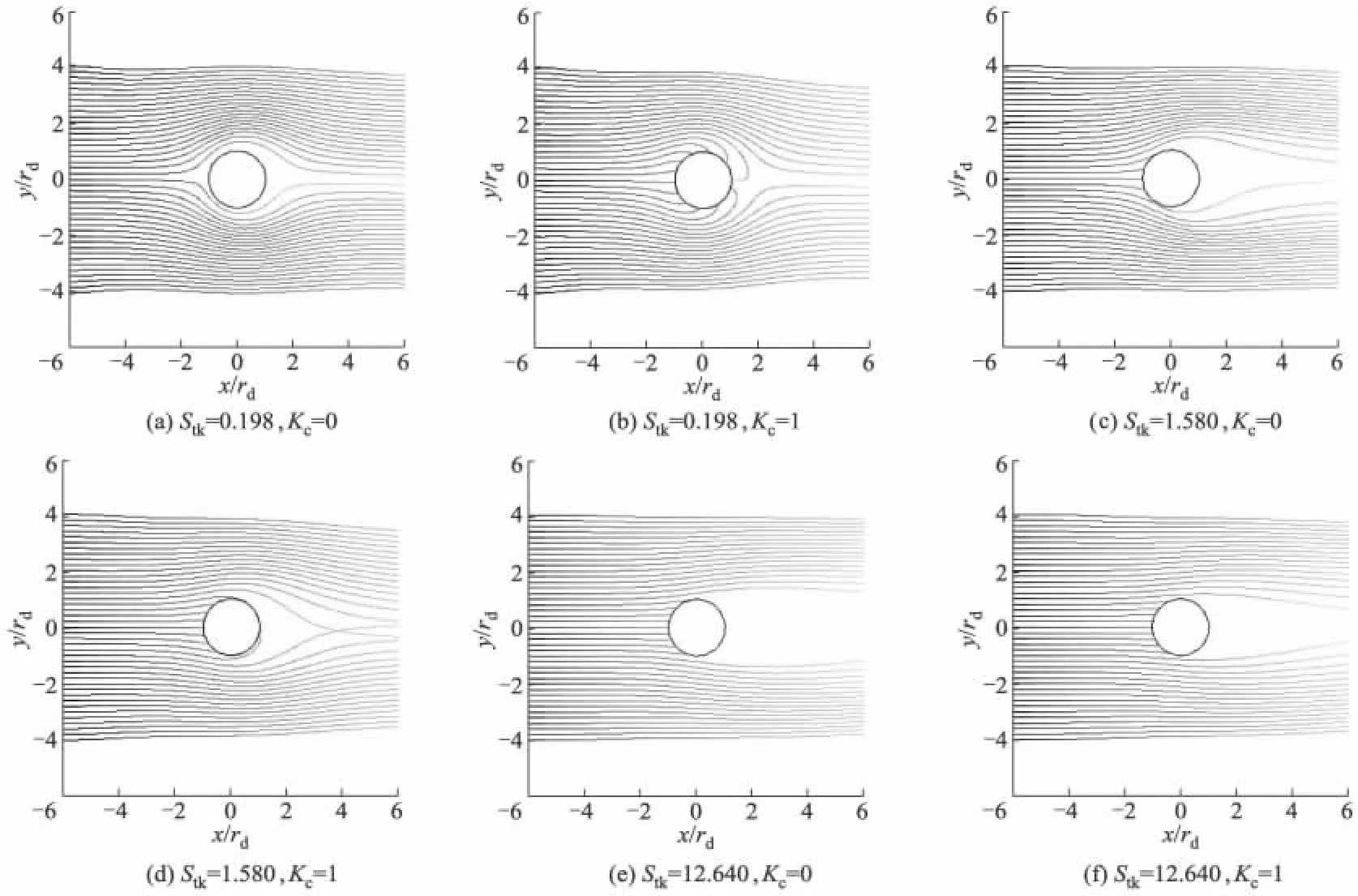
图3 不同Stk，Kc下细颗粒物的运动轨迹示意图

当液滴和细颗粒物均荷电时(Kc=1)，静电力的作用使更多细颗粒物的轨迹偏转向液滴表面，越靠近液滴，静电力的作用越明显.Stk较小时(Stk=0.198)，静电力的作用使颗粒碰撞轨迹的数量大幅增加.此时细颗粒物自身的惯性作用比较小，因此静电力对细颗粒物运动的影响较大，即使是离液滴很远的细颗粒物都会被吸附到液滴表面，并且有相当一部分细颗粒物的沉积发生在液滴的背面.Stk的增大使细颗粒物的惯性作用增强，静电力和气流的拖曳力对细颗粒物的影响都会产生一定的降低.Stk较大时(Stk=12.640)，细颗粒物惯性作用过大，静电力的作用仅能使一部分细颗粒物的运动方向发生偏转，总体的碰撞轨迹数量并没有发生太大的改变.

2.2 Stk和Kc对沉积效率的影响

不同Stk，Kc下液滴吸附面积比的变化示意图如图4所示，在非荷电(Kc=0)的情况下，Stk很小时，液滴的吸附能力几乎为0;随着Stk增大，惯性作用的增强使液滴吸附面积比不断提升，最终趋向于1;对于液滴和细颗粒物均荷电的情况(Kc=1)，当Stk较小(Stk=0.100)时，静电力的作用能使液滴吸附能力得到大幅提升，此时静电沉积占主导地位，随着Stk增大，惯性作用的增强会削弱静电沉积，静电沉积的削弱会强于惯性沉积的增强，液滴吸附面积比随之降低.Stk增大到一定程度时，惯性作用非常强使得惯性沉积占主导地位，因此随着Stk的增大，惯性作用的增强使得惯性沉积量逐步增加，惯性沉积的增长速度会强于静电沉积的削弱速度，因此液滴吸附面积比会逐渐增高，此时静电力的作用能够使液滴的吸附能力有所改善，但效果并不明显.最终当Stk非常大的时候，液滴吸附面积比同样趋向于1.

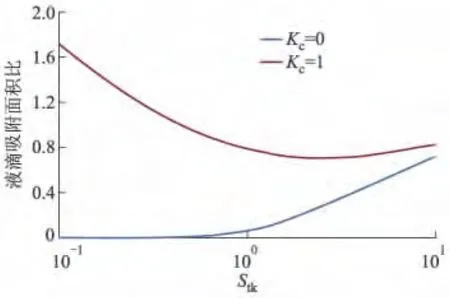
图4 不同Stk，Kc下液滴吸附面积比变化曲线

2.3 计算结果与分析

讨论了Kc以及Stk对液滴吸附能力的影响，这2个量的共同影响参数为气流速度，细颗粒物粒径以及液滴粒径.在实际条件中随着细颗粒物和液滴物性的变化，这2个量很难单独改变.首先当气流速度增加时，根据式(10)，(11)可知Stk增大Kc减小.根据对图4的分析可知:液滴的吸附能力随着气流速度的增加必然呈下降的趋势，因此增大气流速度不利于提升除尘效率.

对于细颗粒物和液滴，首先根据电场荷电模型［7，14］可以计算出液滴和细颗粒物的荷电量:

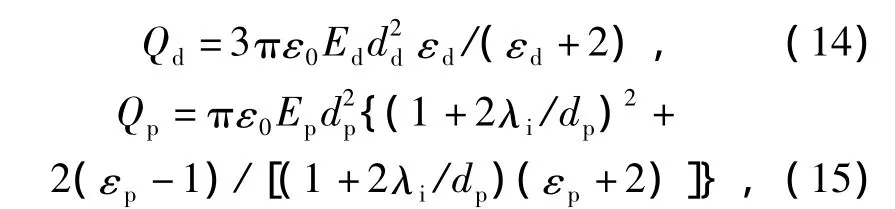
式中:ε0为空气的介电常数;λi为离子平均自由程，λi=10-7m;εd为液滴相对介电常数，取82;εp为细颗粒物的的相对介电常数，取4.0.

对于不同的液滴和细颗粒物粒径，液滴吸附面积比的变化示意图如图5所示.其中液滴选取了50，100，200 μm 这3 种不同粒径，液滴的密度 ρd取1 000 kg·m-3，细颗粒物的密度取 ρp取2 500 kg·m-3，初始气液相对速度u0取1.5 m·s-1，液滴和细颗粒物荷上异性的电荷，荷电场强Ed和Ep均取1 kV·cm-1.

图5 液滴吸附面积比随细颗粒物粒径变化示意图

将式(14)，(15)代入式(11)，当细颗粒物粒径增加时，Stk增大，Kc的变化分为2个部分，对于细颗粒物粒径小于或者略大于离子平均自由程时，随着粒径的增大，单位面积的细颗粒物的荷电量会急剧减小，此时Kc随之减小，之后Kc则会随着细颗粒物粒径的增加而增大.如图5所示，对于不同的细颗粒物粒径，液滴吸附面积比的变化分为几个阶段.当细颗粒物粒径小于0.3 μm时，细颗粒物粒径增加导致Stk提升和Kc减小使得静电沉积量大幅减小，Stk提升所带来的惯性沉积量的增加完全可以忽略，因此液滴吸附面积比呈不断下降的趋势.

J.H.Kim等［2］通过试验研究静电除尘和静电湿式除尘这2种技术单独采用和叠加使用对除尘效率的影响.试验所采用的细颗粒物的粒径区间为0.1～0.3 μm，当单独采用静电湿式除尘技术吸附细颗粒物时，沉积效率随着细颗粒物粒径的增加而不断降低，与图5的结果相吻合.当细颗粒物的粒径大于0.3 μm时，Kc开始随着细颗粒物粒径的增加而增大，静电沉积量不断提升，液滴的吸附能力逐渐增强，而当细颗粒物粒径增大至3 μm之后，从图5中可以看出:对于液滴粒径为50 μm以及100 μm的情况，液滴吸附面积比有2次下降，产生下降的原因均是细颗粒物的惯性作用的提升导致的静电沉积的削弱，而中间产生了1次小幅的反弹，它的原因是静电沉积减少的同时，细颗粒物自身的惯性沉积也在增加，在这一区间惯性沉积量的提升速度超出了静电沉积的减少速度，而对于粒径为200 μm的液滴，由于在这一区间静电沉积作用仍然非常强，因此这一现象没有发生，仅仅使液滴吸附面积比的下降速度有所缓和.

当液滴粒径增加时，Stk减小，Kc不变，静电引力作用不变，而惯性作用对静电沉积的削弱减弱，因此对于单个液滴，大粒径的液滴有较强的吸附能力.而实际中，考虑到液滴的分布密度，相同的气液比下单位空间内小粒径的液滴的个数远远超过大粒径的液滴.相同的气液比下，存在一个200 μm的液滴的空间中如果换成50 μm的液滴，液滴的数量将变成64个，将相同气液比下多个小粒径的液滴的吸附面积的总和与单个200 μm的液滴的截面积之比，得出的结果如图6所示，相同气液比下小粒径的液滴对细颗粒物的吸附量远远超过大粒径的液滴.

图6 相同气液比下液滴吸附面积比变化示意图

3 结论

1)Stk较小时，未荷电情况下，细颗粒物对气流有良好的跟随性，大部分细颗粒物跟随气流逃逸，此时荷电能大幅增加颗粒碰撞轨迹的数量，且沉积发生在液滴的整个表面.Stk较大时，细颗粒物自身的惯性作用较大，未荷电情况下，细颗粒物的运动轨迹几乎呈线性，荷电能使细颗粒物的运动方向发生一定偏转，但效率微弱.

2)细颗粒物的沉积效率主要由Stk和Kc决定.非荷电情况下，沉积效率随Stk的增大而提升;荷电情况下，Stk很小时，沉积效率随Stk增大而降低，而当Stk很大变为惯性沉积占主导时，随着Stk的增大，沉积效率会呈一个缓慢增加的趋势，此时静电力会对沉积效率有所改善，但效果并不明显.

3)模拟结果与试验数据较为吻合.对于粒径小于或者略大于离子平均自由程的细颗粒物，液滴的吸附能力随细颗粒物粒径的增加而减弱;对于粒径为1～10 μm的细颗粒物，静电湿式除尘能达到最佳效果;单个荷电液滴的吸附能力随着液滴粒径的增加而增强，而相同的气液比下小粒径液滴的吸附面积远超过大粒径的液滴.

References)

［1］Yang Linjun，Bao Jingjing，Yan Jinpei，et al.Removal of fine particles in wet flue gas desulfurization system by heterogeneous condensation［J］.Chemical Engineering Journal，2010，156:25-32.

［2］Kim J H，Lee H S，Kim H H，et al.Electrospray with electrostatic precipitator enhances fine particles collection efficiency［J］.Journal of Electrostatics，2010，68:305-310.

［3］Kraemer H F，Johnstone H F.Collection of aerosol particles in presence of electrostatic fields［J］.Industrial and Engineering Chemistry，1955，47(12):2426-2434.

［4］王银生，王英敏.静电喷雾除尘适于微细粉尘的理论分析［J］.东北大学学报:自然科学版，1996，17(3):301-304.

Wang Yinsheng，Wang Yingmin.Theoretical analysis of dust cont rolling of electrostatic spray fitting for fine dust［J］.Journal of Northeastern University:Natural Science，1996，17(3):301-304.(in Chinese)

［5］周新建，陈海安，李勇刚.静电作用下喷雾降尘效率的研究［J］.矿山机械，2010，38(10):61-63.

Zhou Xinjian，Chen Haian，Li Yonggang.Study on efficiency of dust suppression with spraying under influence of electrostatic field［J］.Mining＆Processing Equipment，2010，38(10):61-63.(in Chinese)

［6］Jaworek A，Balachandran W，Lackowski M，et al.Multi-nozzle electrospray system for gas cleaning processes［J］.Journal of Electrostatics，2006，64:194-202.

［7］赵海波，郑楚光.静电增强湿式除尘器捕集可吸入颗粒物的定量描述［J］.燃烧科学与技术，2007，13(2):119-125.

Zhao Haibo，Zheng Chuguang.Quantitative description of removal process if particulate matter in gravitational wet scrubbers with electrostatic enhancement［J］.Journal of Combustion Science and Technology，2007，13(2):119-125.(in Chinese)

［8］袁 颖，王京刚.荷电水雾除尘过程中颗粒运动轨迹的数值模拟［J］.北京化工大学报，2005，32(1):28-32.

Yuan Ying，Wang Jinggang.Numerical simulation for particle trajectory in a spray charging precipitator［J］.Journal of Beijing University of Chemical Technology，2005，32(1):28-32.(in Chinese)

［9］王军锋，姚 江，张宗海，等.外混式双流体雾化器荷电喷雾流场特性［J］.江苏大学学报:自然科学版，2014，35(6):649-655.

Wang Junfeng，Yao Jiang，Zhang Zonghai，et al.Measurement of charged spray flow field for external mixing twin-fluid nozzle by PIV［J］.Journal of Jiangsu University:Natural Science Edition，2014，35(6):649-655.(in Chinese)

［10］王嘉骏，李良超，顾雪萍，等.搅拌反应器内气液两相流的CFD研究进展［J］.化工设备与管道，2012，49(1):1-4.

Wang Jiajun，Li Liangchao，Gu Xueping，et al.Progress on CFD simulation of gas-liquid two-phase flow in stirred tank reactor［J］.Process Equipment＆Piping，2012，49(1):1-4.(in Chinese)

［11］Clift R，Grace J R，Weber M E.Bubbles，Drops and Particles［M］.London:Academic Press，1978.

［12］钱付平，王海刚.随机排列纤维过滤器颗粒捕集特性的数值研究［J］.土木建筑与环境工程，2010，32(6):120-126.

Qian Fuping，Wang Haigang.Numerical analysis on particle capture characteristics of fibrous filters with random structure［J］.Journal of Civil，Architectural＆Environmental Engineering，2010，32(6):120-126.(in Chinese)

［13］Duangsuwan W，Tuzun U，Sermon P A.The dynamics of single air bubbles and alcohol drops in sunflower oil at various temperatures ［J］.AIChE Journal，2011，57(4):897-910.

［14］Long Zhengwei，Yao Qiang.Evaluation of various particle charging models for simulating particle dynamics in electrostatic precipitators［J］.Journal of Aerosol Science，2010，41(7):702-718.