倾斜金标试纸图像的线宽测量方法
2015-02-21陈正伟朱建华刘铁兵
周 律, 陈正伟, 朱建华, 刘铁兵
(浙江科技学院 a.工程实践中心; b.中德农产品加工工业研究院,浙江 杭州 310023)
倾斜金标试纸图像的线宽测量方法
周 律a, 陈正伟a, 朱建华a, 刘铁兵b
(浙江科技学院 a.工程实践中心; b.中德农产品加工工业研究院,浙江 杭州 310023)
基于显微图像的金标试纸条测试线线宽参数的测量方法具备操作方便、测量速度快、分辨率高等优点,然而图像采集系统采集到的金标试纸条的显微图像不可避免地会发生倾斜,这为后续的图像分割和参数测量带来了困难,因此需要对倾斜的金标试纸条显微图像进行校正。根据霍夫变换法和最小二乘法在直线检测中的优点和适用条件,拟采用一种结合霍夫变换法和最小二乘法的直线检测算法来求得金标试纸条图像的边缘线和边缘线的倾斜角度参数,并采用图像旋转变换算法实现对原图像的倾斜校正。实验表明,所采用的倾斜校正算法具备计算量小、占用内存小、校正精度高的优点,通过倾斜校正可以准确测量倾斜金标试纸图像的线宽参数。
自动化仪器仪表与装置; 金标试纸条; 图像传感器; 显微图像; 几何参数测量
0 引 言
金标试纸检测法是近年来迅速发展起来的一种生化检测技术,广泛应用于疾病诊断、食品安全等领域。它应用了抗原、抗体特异性规律和胶体金显色的原理。测试线呈现的颜色的深度和测试线的宽度与待测样品的目标物的浓度成正相关。因此,如何得到测试线线宽度和颜色是这种测量方法的关键[1-4]。基于显微图像测量金标试纸条测试线细节特征的方法具有操作方便、测量速度快、分辨率高等优点。然而图像采集系统采集到金标试纸条的显微图像不可避免会发生倾斜,这为后续的图像分割和参数测量带来了困难,因此需要对倾斜的金标试纸条显微图像进行校正。图像的倾斜校正包括图像边缘线倾斜角检测和图像的旋转变换两大部分,其核心是图像边缘线倾斜角的检测[5]。Hough变换(Hough Transformation,HT)是直线检测的主要方法之一,它具有鲁棒性好、无需启发知识等优点,同时普通的Hough变换算法存在计算的空间、时间开销大和存在虚假直线等缺点。HT的改进算法RHT和PPHT等,通过利用启发式消息来限制HT的累加过程或设置不同点的Hough空间投票权重等方法来消除HT在直线检测上的不足。这些改进的HT算法尽管能节省一些计算的时间和空间的开销,但检测分辨率受时间、空间及图形噪声等因素的限制,不能达到较高的水平[6-15]。与HT方法不同,最小二乘法(Least Square,LS)可以获得给定数据在均方误差意义下的绝对精确直线,达到HT所达不到的检测精度。但是最小二乘法二乘法受“野值”影响大,需要采用一些算法削弱或消除“野值”对检测结果的影响。本文拟采用一种结合霍夫变换法和最小二乘法的直线检测算法来求得金标试纸条图像的边缘线和边缘线的倾斜角度参数,并采用图像旋转变换算法实现对原图像的倾斜校正。从而实现应用投影法测量倾斜金标试纸图像测试线的线宽参数。
1 图像法测量金标试纸条参数的原理
1.1 金标试纸检测原理
金标试纸检测原理如下:当待测溶液浸泡或滴入金标试纸条时,溶液通过吸水纤维的毛细作用,将胶体金一起带到吸附有抗体的测试线T和质控线C上,若溶液中的抗原与测试线上的抗体相对应,则抗体和抗原产生特异性结合,胶体金附着在测试线T和质控线C对应的区域上,从而使该区域呈胶体金的红色或紫红色。测试线呈的颜色的深度和测试线的宽度与待测样品的目标物的浓度成正相关,因此只要检测出测试线呈的颜色的深度和测试线的宽度,就可以推断出待测样品的检测结果。如果是定性判断,则判定测试线颜色深、宽度大的待测样品为阳性;反之为阴性。如果是定量检测,则是通过建立测试线呈的颜色的深度和测试线的宽度与待测样品中待测物质的浓度相对应的标准曲线来得到待测样品的浓度参数。金标试纸条结构如图1所示,金标测量仪的核心就是要测定测试线的颜色深度和测试线的宽度。
本文采用图像法检测量纸条的上述参数,为了提高仪器对金标试纸条的分辨能力,本文在普通的图像传感器前增加了一组显微镜头,组成如图2所示的图像采集系统,通过该系统采集到的图像经过后续算法处理便可得到所需的参数。
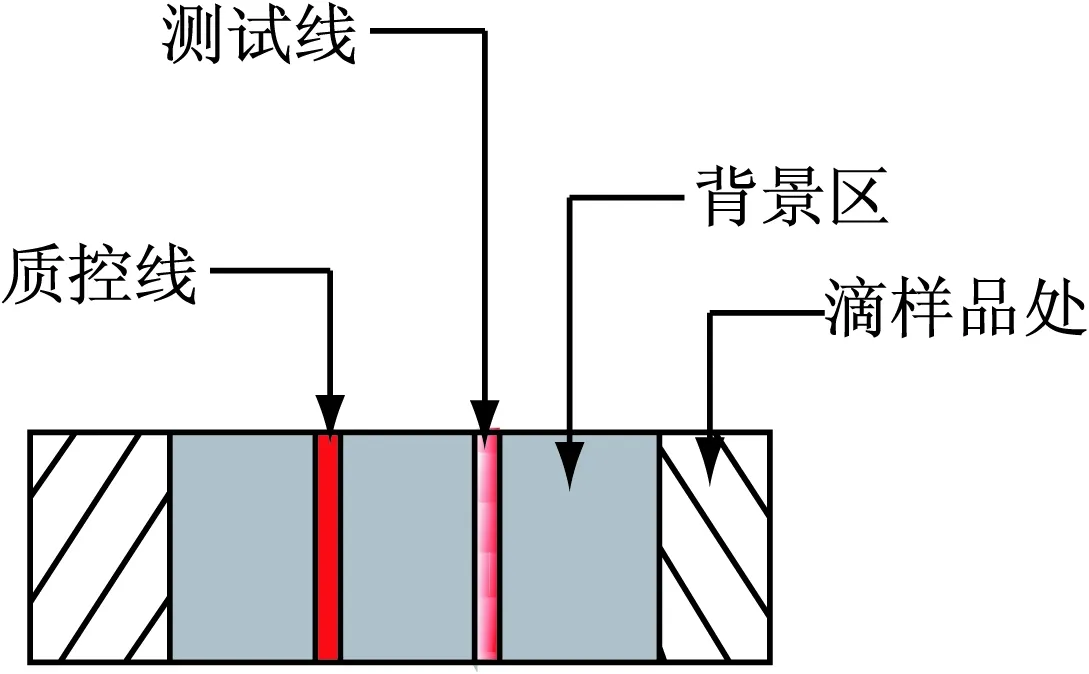
图1 试纸条结构图

(a)框图

(b)实物图
1.2 金标试纸参数测量方法
通过如图2所示的显微图像采集系统,分别采集标准测微尺的图像和待测金标试纸条的图像,并对它们进行相关处理和运算,便可得到金标试纸条测试线线宽参数的值。
1.2.1 求解图像采集系统定标系数K
设测微标尺的实际宽度为L, 显微系统放大倍数为A, 采样密度为Q,对应图像的长度为N(像素点数), 则系统定标值K可表示为:

(1)
1.2.2 通过测试线的像素距离求解实际距离
如果令测试线图像长度为M(像素点数),则测试线的实际宽度D由下公式给出:
D=KM
(2)
通过检测显微标尺图像可以得到系统定标值K,再通过金标试纸条的测试线线宽度的像素值M,便可由式(2)得到金标试纸条的测试线线宽度的真实值。
1.2.3 金标图像的预处理和线宽测量
考虑到金标试纸条图像的颜色偏暗红,图像中的绿色分量最具意义,本文采用式3对图3(a)所示的原始图像进行灰度化,
gray[i,j]=int(c[i,j].G)
(3)
并对得到的图像进行3×3的均值滤波,得到结果如图3(b)所示。
根据图3(b)中所示的金标试纸条图像中测试线和背景的不同灰度值均值,取两部分灰度值的平均值作为分割阈值进行二值化,得到如图3(c)所示的二值化图像。

(a)原始图像

(b)灰度图像

(c)二值化图像
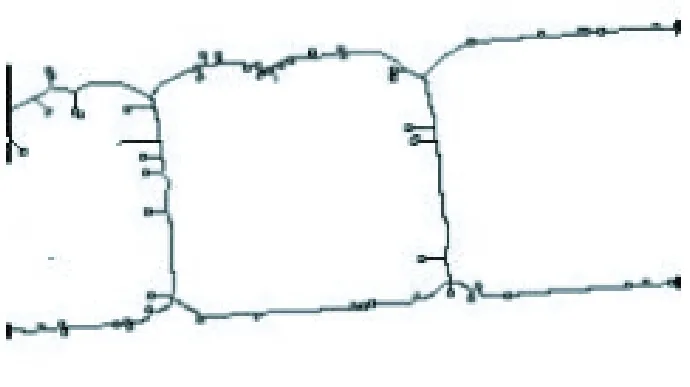
可以看出,测试线边界模糊且呈现不规则的形状。为了提高测量值的稳定性,使不同批次试纸条的测量值具备可比性,本文采用投影法定义金标试纸条测试线线宽D为:令测试线方向为y轴,统计沿x轴方向每一列白色像素点数目,该数值沿x轴的分布如图4所示,线宽D定义为分布图中测试线位置的缺口宽度。

不难发现,上述方法只适合金标试纸条放置水平的情况。然而在测量过程中金标试纸条图像不可避免地会发生倾斜,因此必须对倾斜的金标试纸条显微图像进行校正才能保证测量结果的准确。
2 结合HT与LS的金标图像校正方法
2.1 Hough变换检测直线的基本原理
Hough变换时对二值图像进行直线检测的有效方法之一,其实质是坐标变换,将图像空间的点映射到参数空间,通过变换可以使图像空间的直线或线段容易被检测出来,如图5所示。

图5 Hough变换原理示意图
图中:r为坐标原点到直线l的距离;θ为坐标原点到直线l的垂线与x轴正方向的夹角。图像空间的一条直线可以有参数方程r=xcosθ+ysinθ表示。通过Hough变换,在图像空间直角坐标系下的一条直线映射为参数空间极坐标下的一族具有公关交点的曲线。在参数空间极坐标一点对应于直角坐标系下的一条直线。基于Hough变换检测图像中的直线步骤如下:
(1) 在r、θ合适的最大值和最小值之间建立一个离散的参数空间。
(2) 建立一个累加器A(r,θ),并置每个元素为0。
(3) 对二值图像的每一个非零点作Hough变换,并算出该点在r-θ空间上的对应曲线,并对相应的累加器加1。
(4) 找出对应图像平面共线点的累加器上的局部极大值,这个值所在点的位置参数便是所要检测直线的参数。
2.2LS(最小二乘法)检测直线的基本原理
LS法是最为常见的线性回归方法之一,能够给出均方差意义下的精确直线。应用最小二乘法检测直线的原理如下:
给定的数据集{(xi,yi)|1≤i≤N},待确定的回归直线方程为y=ax+b。则均方误差为:
(4)
E取最小值时有:

因此有:
(5)
其中:
如果写成r-θ参数方程可得:
2.3 结合HT和LS的金标图像校正方法
结合Hough变换和最小二乘法的金标图像校正方法利用Hough变换具备的鲁棒性且无需启发式信息的优点和最小二乘法能确定待检测直线的精确参数的特性对图像边缘直线参数进行高效精确的检测,并利用图像旋转变换实现图像的校正。其主要步骤如下:
(1)给定二值图像I、HT的参数分辨率(Δr,Δθ)、HT投票数阈值T以及直线所在大致区域的距离误差限d。
(2)在分辨率(Δr,Δθ)下求取I得标准Hough变换,并确定投票值不小于T的直线参数点。
(3)对检测到的直线参数点,在I中寻找所有到该直线距离大于d的特征点,构成特征点集L。
(4)对L进行最小二乘法直线拟合,得到最终的图像边缘直线及其倾斜角参数(θq)。
(5)应用图像旋转算法将原图像整体旋转-θq角度得到校正后的图像。
通过最小二乘法的直线检测方法提高了直线的检测率和检测精度,且降低了对Hough变换的分辨率要求,从而减小算法整体的空间开销。
3 结果分析
3.1 倾斜金标试纸图像的校正
对采集到的倾斜的金标试纸图像进行1.2节所述的方法进行预处理,得到图6(b)所示的二值化图像,可以发现试纸条的边缘线较宽,无法进行直接的边缘线检测,因此本文应用Rosenfeld细化算法对图6(b)所示的图像进行细化处理得到图6(c)所示的细化后的图像,然后对图6(c)所示的图像应用本文提出的结合Hough变换和最小二乘法的直线检测算法得到图6(d)所示的边缘直线。并用边缘直线的参数对原图进行倾斜校正得到图7所示的校正后的图像。最后对倾斜校正后的金标试纸图像按照1.2节所述的参数测量方法对金标试纸图像的测试线线宽进行有效地测量。

(a)原图 (b)预处理过的二值化图像

(c)细化后的二值化图像 (d)检测到的边缘直线
图6 校正处理过程

(a)彩色像

(b)二值化后的图像
3.2 参数测量结果分析
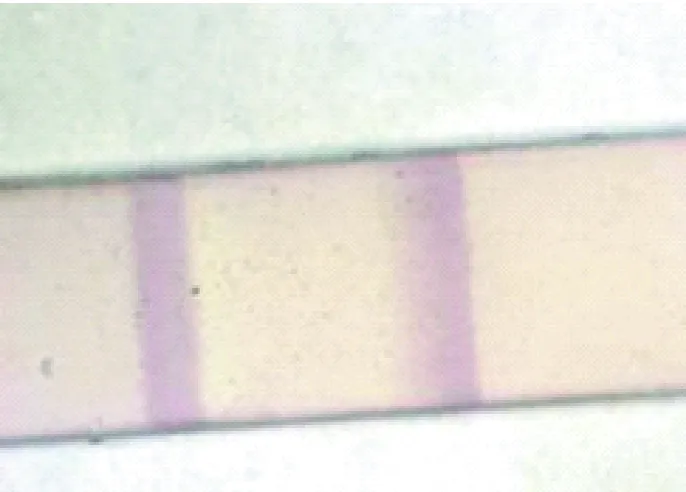
先由显微标尺图像得到系统的定标系数K=0.005 387 mm/pixel,再由图4求得金标试纸条测试线线宽像素值M为170 pixel,从而得到金标试纸条测试线线宽D为0.92 mm。将同一金标试纸条用最小刻度0.1 mm的测微标尺直接观察,如图8所示,可以看到测试线的宽度在0.8~1.10 mm之间,从而证明本文的基于显微图像的测试线线宽测量结果是正确可信的。
4 结 语
本文采用投影法测量金标试纸图像测试线线宽参数,为了保证线宽测量的有效性,采用结合Hough变换和最小二乘法的的金标图像校正方法,利用Hough变换具备的鲁棒性且无需启发式信息的优点和最小二乘法能确定待检测直线的精确参数的特色,在保证直线的检测率和检测精度的前提下,减小算法整体的时间、空间开销。实验证明本文提出的倾斜金标图像测试线线宽参数的测量结果是正确可信的。

图8 显微标尺与金标试纸条对照结果图像
[1] 杜 民,方志成. 金标试条定量测量仪器的研究[J].仪器仪表学报,2001,22(6):626-628.
[2] 余厚云,邓善熙,杨永跃,等. 用Visual Basic 6.0编程实现显微图像测量[J].微计算机信息,2003(2):67-68.
[3] 邹翠霞,崔玉影,王崇杰. 显微数字图像系统的尺度定标方法[J] .大连工业大学学报,2008,27(1):26-29.
[4] 王慧敏,杨成文,赵友全.基于视觉成像的生物安全金标试条检测仪[J]. 光谱仪器与分析,2009(Z1):170-175.
[5] 艾朝霞.基于Hough变换的改进的纸币倾斜校正方法[J] .科学技术与工程,2011,11(20): 4976-4978.
[6] Duda R O. Hart P E. Use of the Hough transform to detect lines and curves in pictures [J].Communications of the ACM,1972,15(1):11-15.
[7] Xu L, Oja E. Randomized Hough Transform(RHT):Basic mechanisms, algorithms, and computational complexities[J].Computer Vision, Graphics, and Image Processing-Image Under-standing,1993,57(2):131-154.
[8] Matas J. Robust detection of line using the progressive probabi-listic hough transform[J]. Computer Vision and Image Under-standing, 2000, 78(1):119-137.
[9] 孙燮华. 数值图像处理—原理与算法[M] .北京:机械工业出版社,2010:80-100.
[10] 徐胜华,朱 庆,刘纪平,等.基于预存储权值矩阵的多尺度Hough变换直线提取算法[J].测绘学报,2008,37(1):83-88.
[11] Dahyot R. Statistical Hough transform[J]. IEEE Trans. on Pat-tern Analysis and Machine Intelligence, 2009, 31(8):1502-1509.
[12] Guo S Y, Prodmore T, Kong Y G,etal. Improved Hough trans-form voting scheme utilizing surround suppression[J].Pattern Recognition Letters,2009,30(13):1241-1252.
[13] 魏志强,孙亚兵,纪筱鹏,等.数字城市中矩形建筑物区域的自动获取[J].计算机科学,2009,36(1):211-215.
[14] 郭斯羽,翟文娟,唐 求,等.结合Hough变换与改进最小二乘法的直线检测[J].计算机科学,2012,39(4):196-200.
[15] 张 佳, 程宇龙. 基于随机Hough变换的圆形目标检测实验[J]. 实验室探索与研究,2014(7):130-133.
Study on Detection Method of the Width Parameters of Slanted Colloidal Gold Strip Image
ZHOULüa,CHENZheng-weia,ZHUJian-huaa,LIUTie-bingb
(a. Center of Engineering Practice; b. Zhejiang Provincial Key Lab for Chemical & Biological Processing Technology of Farm Product, Zhejiang University of Science and Technology, Hangzhou 310023, China)
The width parameter detection method based on colloidal gold strip microscopic image has lots of merits such as easy operation, high testing speed, and high resolution. However, the colloidal gold strip microscopic image is inevitable slanted by many factors. The slanted image is difficult to be segmented and measured. So it is necessary to rectify the slanted image before it is segmented and measured. According to the advantages of Hough transform method and the least-square method in the line detection, a method combining Hough transform and the least-square is proposed to detect the edge lines of the colloidal gold strip microscopic image and find the angle parameters of the edge lines. Image rotation algorithm is used to rotate the slanted image and get the correction image. Experiments show that the method has high detection precision with less computer memory and shorter calculation time, and the measure result is accurate.
electrical instruments and apparatus; colloidal gold strip; image sensor; microscopic image; geometrical parameter measurement
2014-08-14
浙江省教育厅科研计划项目(Y201225526)
周 律(1967-),男,浙江杭州人,工程师,实验师,主要研究领域为自动化及电工电子技术。
Tel.:13336002527;E-mail:zhou_lv@126.com
TP 216.3
A
1006-7167(2015)03-0146-04
