基于多个混沌系统和位运算的图像加密算法

浩 明

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)



基于多个混沌系统和位运算的图像加密算法

浩 明

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

为了有效改进图像加密效果及安全性，在对基于混沌系统及位运算的图像加密算法进行研究的基础上，提出了一种改进的基于多个混沌系统和位运算的图像加密算法。首先对任意大小灰度进行位平面分解，利用Logistic混沌映射进行混沌排序置乱，再分解成若干个二值图像，利用2-DArnod变换进行置乱，最后对加密后的二值图像组合，生成密文图像。实验结果表明，与置乱扩散加密算法比较，改进算法具有更好的加密效率，密钥空间接近2136，具有较好的安全性，且能较好地抵御擦除和椒盐噪声攻击，有效恢复出原始图像。

混沌； 图像加密； 置乱； 位平面； 分段非线性映射

0 引 言

随着网络和信息技术的发展和普及，信息安全问题日益突出，其中图像等多媒体数据的安全问题也日益引起人们的关注。由于数字图像具有冗余度高、数据量大、数据相关性强等特点，采用传统的加密方式进行加密将导致加密速度慢、实时性差等缺点。如何结合数字图像的特点设计有效的数字图像加密算法成为信息安全领域的一个研究热点。

混沌系统具有初值敏感性、非周期性、非收敛性、伪随机性等良好的密码学特性，是非线性确定系统由于内在随机性而产生的外在复杂表现，是一种貌似随机的非随机现象。混沌系统的这些特点使其被广泛应用于数据加密技术[1-5]。

当前，基于混沌的数字图像加密方式主要包括基于置乱的加密技术、基于灰度替换的加密技术和基于混合迭代结构的图像加密技术[6-10]。其中，基于像素位置置乱的加密算法虽然可以实现图像加密的目的，但其安全性较差，无法满足实用性的需求。由于像素置乱加密图像的方式存在可恢复周期等安全隐患，研究者进一步提出了将像素位置置乱和灰度替代相结合的加密方式，这类混合迭代结构的加密方式可以有效提高算法的安全性。

本文研究了基于混沌和位运算的图像加密算法[11-18]，在此基础上，给出了一种改进的基于多个混沌和位运算的图像加密算法，理论分析和实验结果表明，改进算法具有较好的加密效果和安全性。

1 Logistic映射及其特性

1.1 Logistic映射

Logistic 映射是一种典型的一维混沌系统，定义如下：

(1)

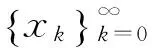
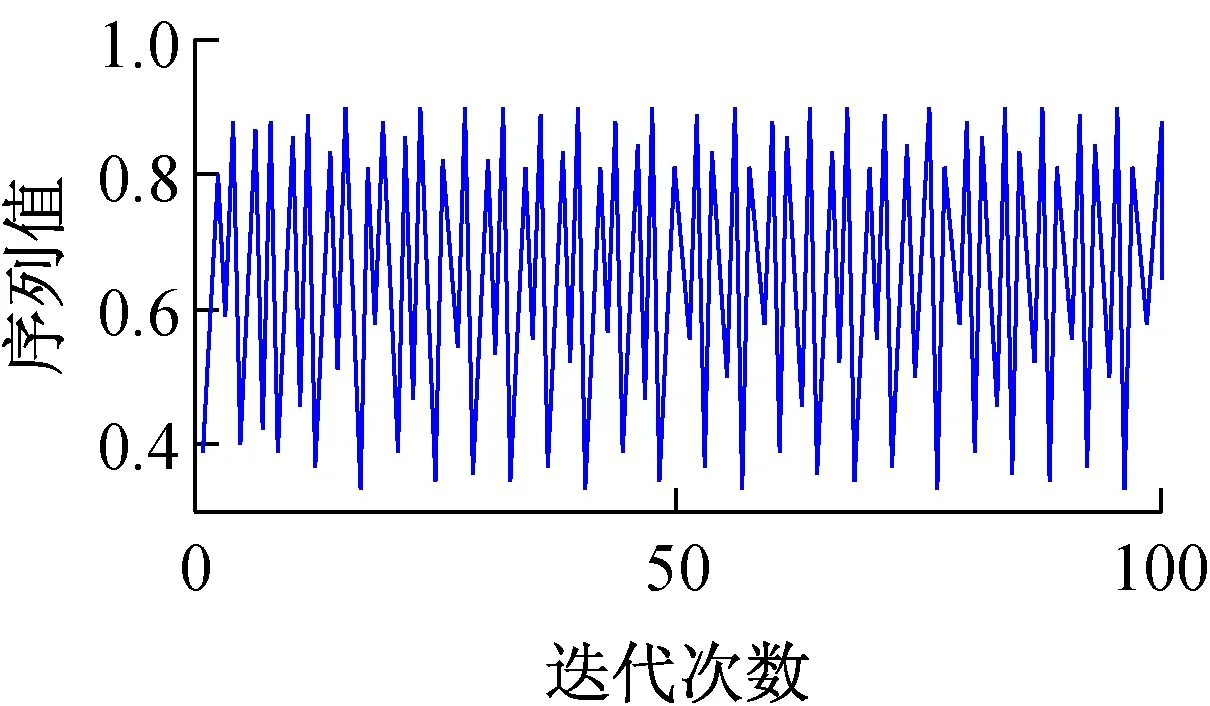
(a)x0=0.333 3

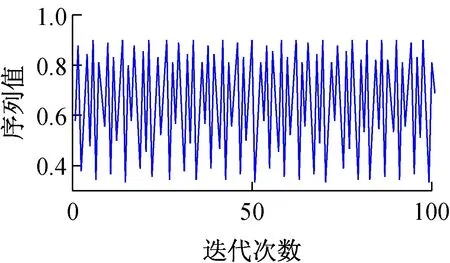
(b) y0=0.565 6

图1 给出了当μ=3.578 9，x0=0.333 3，y0=0.565 6时，应用式( 1) 进行迭代计算得到序列的分布情况。实验结果表明，迭代计算得到的序列具有良好的非周期性、非收敛性以及对初始条件的敏感性。

1.2 混沌的特性

Logistic混沌具有遍历性、非周期性、长期不可预测性以及非收敛性等优良的混沌性质。应用Logistic映射产生序列的概率密度函数、混沌轨迹的平均值、序列的自相关系数和互相关系数有如下特点：

混沌系统产生序列的概率密度函数：

(2)

混沌序列轨迹点的平均值：

(3)

混沌序列的自相关系数：

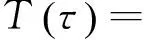
(4)

混沌序列的互相关系数：

(5)

1.3 基于混沌置乱的图像加密方法

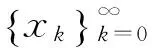
(a)原始图像(b)原始图像直方图

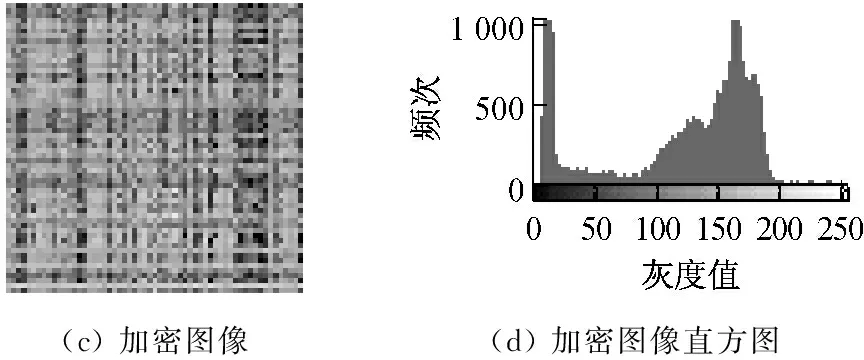
(c)加密图像(d)加密图像直方图

图2 加密效果

图2的实验结果表明，像素级别的图像置乱加密算法，原始图像和密文图像的灰度直方图没有发生改变，说明基于位置置乱的图像加密方式不改变图像的灰度统计信息，这种特点将影响加密结果的安全性，使得加密结果不能有效抵抗统计分析攻击。因此，本文给出一种改进的基于混沌和位运算图像加密算法。

2 算法原理

2.1 基于混沌和位运算图像加密算法

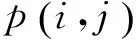
由下式将一幅灰度图像转换为由0和1组成的二值矩阵，

(6)

下式可将二值图像恢复成灰度图像，

(7)

以大小为M×N 灰度图像为例，由式( 6) 可转化成大小为M×8N，像素值由0和1组成的二值图像。

加密过程如下：

(1) 首先读取一幅大小为M×N的灰度图像A；

(2) 由式(6)将图像A转换为M×8N的二值图像，记为B；

(3) 由式(1)产生混沌序列，构造行、列置乱向量，置乱图像B，得图像C；

(4) 用式(7)对图像C进行变换，得大小为M×N的密文图像D。

图3给出了相应的的仿真结果。

(a)Lena图像(c)密文图像

(b)明文直方图(d)密文直方图

图3 图像置乱加密结果

图3的实验结果表明，基于Logistic和位运算图像加密算法所得密文图像的灰度直方图均匀性较差，加密效果较差，无法保证图像的安全性。因此，本文对该方法进行了改进，采用多个混沌系统和位运算构造图像加密方法。

2.2 改进算法及其分析

改进的加密算法包括两个迭代置乱阶段。首先对原始图像实施位平面分解，采用混沌排序算法对位平面进行置乱，然后将置乱后的位平面分成若干个二值矩阵，对每个二值矩阵分别采用Arnold变换进行置乱加密，最后将这些置乱后的二值矩阵合并，产生密文图像。为了充分扰乱原图像中相邻像素的相关性，隐藏明文和密文之间的关系，将Arnold 变换迭代m轮，再将整个置乱过程迭代n轮。由于两个阶段的迭代操作都在位平面上进行，所以每个置乱过程不仅实现了对像素位置的置乱，也改变了像素值，算法取得了扩散的效果，有效地解决了基于置乱加密技术的两个缺点。

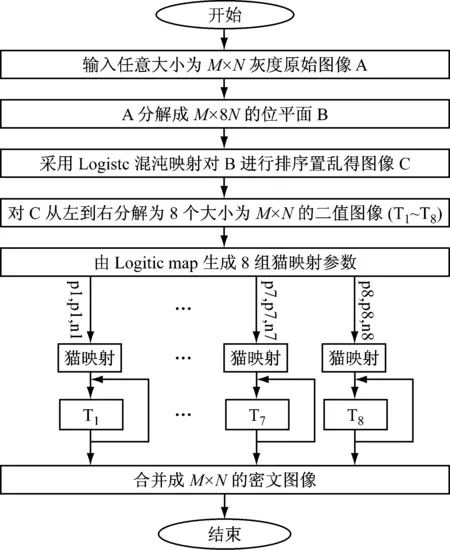
加密过程如下(见图4)：

(1) 首先读取一幅大小为M×N图像A，见图5。

(2) 由式(6)将图像A转换为M×8N的二值图像，记为B，见图6。

(3) 由式(1)产生混沌序列，构造行、列置乱向量，置乱图像B，得图像C，见图7。

(4) 对C从左到右分解为8个大小为M×N的二值图像T1～T8，见图8。

(5) 应用猫映射来置乱这8个二值图像，图3中8组猫映射置乱参数piqi和迭代次数ni取值方法如下：① 首先，迭代式(1)P次，使混沌映射越过暂态效应，进入稳定状态，P为整数；② 分别取初始条件x1,y1,μ1得到两组混沌序列x,y；③ 由下式获取8组猫映射迭代次数和置乱参数，

(8)

考虑到计算复杂度，本文采用固定的参数和迭代次数，对图8的8个位平面进行置乱操作。每个位平面所需猫映射的参数分别为p1=40,q1=9,p2=35,q2=8,p3=30,q3=7,p4=25,q4=6,p5=20,q5=5,,p6=15,q6=4,p7=10,q7=3,p8=5,q8=2，迭代次数统一取n=3，实验结果见图9。

(6) 合并这8个二值图像为一个大小为M×N的灰度图像，即为加密图像。

图5 原始Lean图像

图6 原始Lean图的位平面

图7 置乱位平面

(a)(b)(c)(d)

(e)(f)(g)(h)

图8 从左到右分解的8个二值图像T1～T8

(e)(f)(g)(h)

图9 猫映射置乱后的8个位平面

图10给出了应用改进算法的实验结果。比较图3和图10的加密结果和灰度直方图可以发现，改进算法加密的密文图像的灰度直方图更加均匀，原始图像经过加密后，其统计特性完全被打乱，因此密文图像更具有抗统计分析的能力，安全性更高。

3 算法分析

3.1 密钥空间和敏感性分析

(a)原始图像(b)密文图像

(c)明文直方图(d)密文直方图

图10 密文图像及其灰度直方图

(1) 密钥空间分析。足够大的密钥空间可以抵抗鲁棒攻击。本文加密方案的密钥由两部分组成：① Logistic映射的初始条件为x0、μ0；② 猫映射置乱参数和迭代次数。

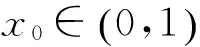
(9)

因此，本文总密钥数为K≈248×248×248/2×2≈2136，足以抵抗统计分析分析等各类非法攻击。

(2) 密钥敏感性测试。加密过程选取

x0=0.123 456 789 123 42，μ0=3.999 99，

x1=0.987 654 321 123 42，

y1=0.432 198 765 123 42，μ1=3.999 99

作为初始参数，8个位平面进行的猫映射迭代次数均取值为1。图11(c)是仅当x0=0.123 456 789 123 41，其他参数都正确取值的解密图像，图11(d)是仅当x1=0.987 654 321 123 41，其他参数都正确取值的解密图像。

(a)原始Vase图像(b)密文图像

(c)x0=0.12345678912341(d)x1=0.9876543211234

图11 密钥敏感性测试

图11的实验结果表明，在密钥参数改变微小的情况下，解密图像跟原始图像完全不一样，无法正确解密明文图像。因此，本文算法具有较强的密钥敏感性。

3.2 灰度直方图

图像灰度直方图用以描绘图像每个灰度级的像素数占像素总数的比例。密文图像像素灰度分布非常重要，它隐藏了明文的冗余特性以及明文和密文之间的关系。

图3和图10的实验结果表明，改进算法的密文图像的灰度直方图更加均匀，原始图像经过加密后，其统计特性完全被打乱，因此密文图像更具有抗统计分析的能力，安全性更高。

3.3 图像信息熵

图像的信息熵表示图像灰度值的概率分布情况，图像灰度分布越均匀，图像的信息熵越大。密文图像的信息熵越大，表明加密后的图像灰度值的分布越均匀，攻击者越是难以从原始图像中获取图像的有用信息，加密算法的安全性能更高。图像信息熵H可由下式计算：

(10)

其中:Pi表示灰度值为i的像素出现的概率;M表示图像的灰度等级。对于一个灰度为256的密文图像，其熵近似等于8。如果密文图像的信息熵小于8，那么密文将存在一定的可预测度，将导致密文图像的安全性降低。表1列出不同加密方案所得明文图像和密文图像的信息熵。从表中可以看出，改进算法所得密文图像的信息熵最接近8，说明加密后的图像具有更高的不确定性，且接近置乱扩散加密算法的加密效果。说明改进加密算法足以抵抗熵攻击和差分攻击，保密性良好。

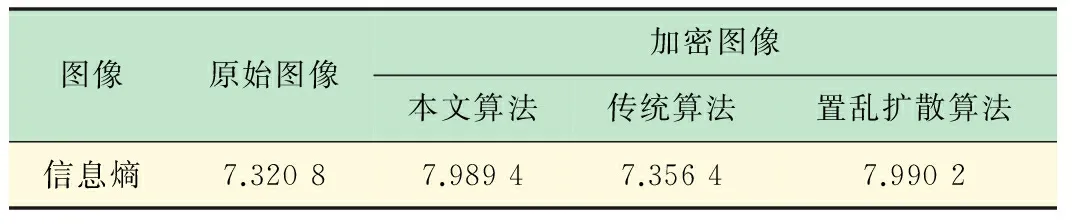
表1 明文与密文信息熵

3.4 抗攻击性测试

由于密文图像在开放的互联网环境，以及受噪声污染的传输信道进行传输，造成失真等原因，难免会受到一些攻击和破坏。一方面考虑到人为的非法攻击，如人为裁剪、破译攻击、涂污等破坏；另一方面传输过程中，传输信道不理想，对图像的传输存在一定的影响；还有在存储过程中，有损压缩造成图像信息的丢失。因此，这就对加密算法的抗攻击和破译性提出了更高的要求，要保证图像信息的完整和可译性。

本文对密文图像进行抗攻击测试，进行了高斯噪声、椒盐噪声和几何擦除等干扰，实验结果如图12所示。结果表明，高斯对图像的恢复影响较为明显，擦除和椒盐噪声的影响较小。实验表明，即使密文图像在受损情况下，仍能较好地解密出原图像，表明该算法具有一定的抗损坏能力，对多种攻击手段都具有较好的鲁棒性。

(a)无噪声(b)高斯噪声测试

(c)垂直方向5%擦除噪声(d)椒盐噪声

图12 不同干扰下受损密文图像的解密图像

4 结 语

本文提出了一种改进的基于混沌和位运算图像加密算法，该算法结合像素灰度替代和位运算进行图像加密。理论分析和实验表明，该算法具有强大密钥空间、良好的灰度直方图、灰度差异度，具有更高的抗攻击能力，加密后的密文图像可以直接用于互联网的安全传输，具有较好的实用性和安全性。

[1] 张小华，刘 芳，焦李成.一种基于混沌序列的图象加密技术[J].中国图像图形学报，2003，8( 4) : 374-378.

[2] 李晓轩，王阿川.一种基于混沌排序的数字图像置乱算法[J].黑龙江科技信息，2009( 27) : 54-54.

[3] 赵学峰.基于面包师变换的数字图像置乱[J].西北师范大学学报: 自然科学版，2003，39( 2) : 26-29.

[4] 顾勤龙，姚 明.基于Logistic 混沌序列的数字图像加密研究[J].计算机工程与应用，2003，23( 3) : 114-116.

[5] 郭建胜，金晨辉.对基于广义猫映射的一个图像加密系统的已知图像攻击[J].通信学报，2005，26( 2) :：131-135.

[6] 曹建秋，肖华荣.像素位置与像素值双重置换的混沌加密算法[J].计算机工程与应用，2010,46(28)：192-195.

[7] 王云才, 马建议, 韩晓红, 等. 混沌激光相关法测距系统的信号采集与处理[J]. 应用光学，2011，32(3)：568-573.

[8] WANG Y，WONG K W.A chaos-based image encryption algorithmwith variable control parameters[J].Chaos， Solitons & Fractals，2009， 41( 4) : 1773-1783.

[9] 孙 鑫，易开祥，孙优贤.基于混沌系统的图像加密算法[J].计算机辅助设计与图形学学报，2002，14( 2) : 136-139.

[10] 张 健，于晓洋，任洪娥.基于Cat 映射和Lu 混沌映射的图像加密方案[J].电子器件，2007，30( 1) : 155 -157.

[11] FU CONG，LIN BINBIN，MIAO YUSHENG，etal.A novel chaos based bit-level permutation scheme for digital image encryption[J].Optics Communications，2011，284( 23) : 5415 -5423.

[12] YE G D.Image scrambling encryption algorithm of pixel bit based on chaos map[J].Pattern Recognition Letters，2010，31(5) : 347-354.

[13] ZHU Z L，ZHANG W，WONG K W，etal.A chaos-based symmetricimage encryption scheme using a bit-level permutation[J].Information Sciences: an International Journal，2011，181( 6) : 1171-1186．

[14] 张雪锋，范九伦.基于位运算的数字图像隐藏技术[J].信息安全与通信保密，2007( 5) : 149-150．

[15] 许 艳.基于位运算的BMP 图像加密算法研究[J].湖南理工学院学报，2007，20( 4) : 41 - 43.

[16] 袁 玲，康宝生.基于Logistic 混沌序列和位换的图像置乱算法[J].计算机应用，2009，29( 10) : 2681-2683.

[17] 李 涛，柳 健.基于位平面与混沌系统的图像置乱方法[J].西南民族大学学报: 自然科学版，2009，34( 3) : 595-599.

[18] 单佳佳，朱灿焰.基于位运算的图象加密技术的研究[J].电脑知识与技术，2007( 5) : 804-805.

[19] Institute of Electrical and Electronics Engineers. IEEE Standard 754 for Binary Floating-Point Arithmetic [S/OL]. (2001-08-06)[2012-1-1], http://www.cs.berkeley.edu/～wkahan/ieee754status/IEEE

Image Encryption Algorithm Based on Multiple Chaotic Systems and Bit Operations

HAOMing

(School of Telecommunication and Information Engineering,Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

In order to effectively improve the image encryption effect and safety, after studying image encryption algorithm based on chaotic systems and bit operations，an improved image encryption algorithm which is based on multiple chaotic systems and bit operations is proposed. Firstly, the original image is decomposed into bit-planes, and chaotic sequence scrambling is done by using Logistic chaotic map, and then it is divided into several binary images. Each divided bit plane is operated by 2-DArnod transformation to scramble. Finally, the encrypted binary images are combined to obtain the final ciphertext image. The experimental result shows that compared with diffusion scrambling encryption algorithm, the modified algorithm achieves a better encryption, and the key space is near to . It has a better security and can be against the attack of and salt-pepper noise. It also can recover the original picture.

chaos; image encryption; scrambling operation; bit plane; piecewise nonlinear mapping

2014-05-22

国家自然科学基金项目(No.61102095);陕西省自然科学基础研究计划项目(No.2012JQ8045)

浩 明(1978-)，男，陕西泾阳人， 工程师， 现从事信息安全研究。Tel.:15339041715; E-mail:imihm@aliyun.com

TP 301.6

A

1006-7167(2015)03-0035-05