基于物理散射的单基地海底混响建模与仿真分析
2015-02-21胡明陈立纲海军驻杭州地区军事代表室杭州310023
胡明 陈立纲(海军驻杭州地区军事代表室,杭州,310023)
基于物理散射的单基地海底混响建模与仿真分析
胡明 陈立纲
(海军驻杭州地区军事代表室,杭州,310023)
摘要分析了海底混响包络非瑞利化的原因,将基于物理过程的K分布混响模型和Jackson海底散射模型相结合,建立了基于物理散射的单基地海底混响仿真模型。将海底混响统计特性与声呐波束宽度、带宽、频率、掠射角等系统参数和散射体尺寸、散射强度、分布密度等环境参数联系起来,同时兼顾了海底混响的统计特性和物理形成机制,仿真结果验证了模型的有效性。
关键词海底混响;K分布;物理散射;统计特性;仿真
海底混响是主动声呐特别是探测沉底及掩埋小目标声呐的主要干扰,由于目标位于海底界面附近且静止不动,导致目标的回波信号与海底混响干扰在时频域上难以分离,给目标的探测带来了极大的困难。为了改进和提高现有的针对界面附近目标的主动声呐探测水平,必需对海底混响场的统计特性及物理机制进行深入研究,以针对该类主动探测问题开发出有效的水声探测技术和信号处理手段;另一方面,由于试验数据的不完备性和试验条件的不可控性,出现了许多针对混响仿真的模型和方法,以方便在实验室实现对水声设备和算法的仿真测试,建立一个较为精确的、可信度较高的海底混响模型可以为算法开发和验证提供数据支撑,以弥补试验数据的不完备,提高算法的可信度和稳健性,这一切都依赖于对海底混响特性的深入研究。
1 海底混响的统计模型
1.1混响统计特性概述
混响统计理论认为如果在一个单元格内的散射体的数目很多,根据中心极限定理,匹配滤波输出的正交和同相成分服从高斯分布,其包络概率密度函数(PDF)服从瑞利分布,这就是传统的瑞利分布混响理论的前提[1]。然而,随着现代声呐分辨率的提高,声呐单个分辨单元内的有效散射体的数量减少,以至于某时刻对混响有贡献的散射体数目不足以符合中心极限定理,亦或是存在若干强散射元时,混响的匹配滤波输出包络概率密度函数将偏离瑞利分布,而趋近于各种形式的非瑞利分布,或称广义瑞利分布。非瑞利分布主要表现为概率密度函数后端较瑞利分布有更严重的拖尾现象,因此在检测时必然会导致虚警概率增大,对接收机的性能造成一定的影响。
1.2基于物理过程的K分布混响模型
在众多非瑞利混响中,K分布模型将混响形成的物理过程与概率密度函数联系起来,因其具有明显的物理意义而受到研究人员的重视。K分布最初由Jakeman和Pusey提出用于描述雷达海杂波干扰的统计特性上[2],认为当散射体的个数n(t)服从负二项式分布且均值趋于无穷时,混响包络的极限分布就服从K分布,其概率密度函数可以写为:
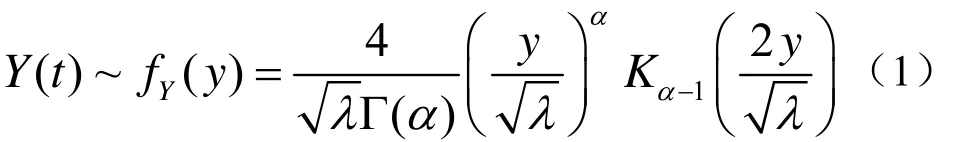
对应的累积分布函数为:

Abraham和Lyons将K分布统计模型引入到声呐领域[3-6],从海底散射的物理现象出发,提出并证明了由有限个尺度服从指数分布的散射元形成的混响的复包络的模服从K分布,并将混响包络K分布统计特性与声呐的波束宽度、带宽、频率、掠射角等系统参数和散射体尺寸、散射强度、分布密度等环境参数联系起来[7-10],建立了K分布混响仿真模型,探讨了K分布混响假设下的宽带信号检测问题,初步确立了K分布混响的理论体系。
考虑单基地混响,假设混响是由声呐照明场内尺度服从指数分布的有限个离散散射体的回波信号在接收点迭加形成的,每个散射体的回波信号的幅度与其几何尺度成正比,记为:
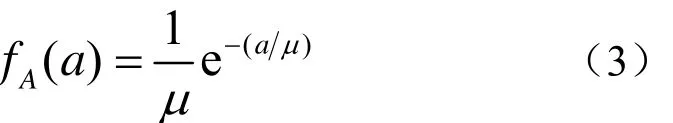
其中,μ为散射体的平均尺度。假设各散射体的幅度和延迟彼此独立,各散射体之间不存在二次散射,并令:
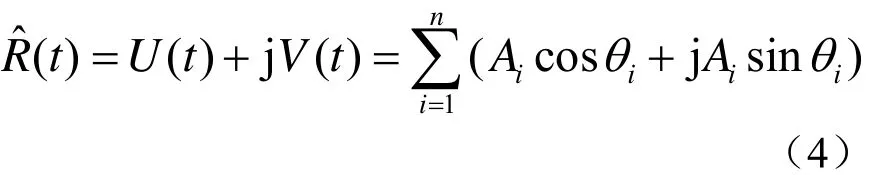


这样,就把实际的声呐系统和海洋环境参数与K分布的参数联系起来,从而使K分布混响模型具有实际的物理意义。
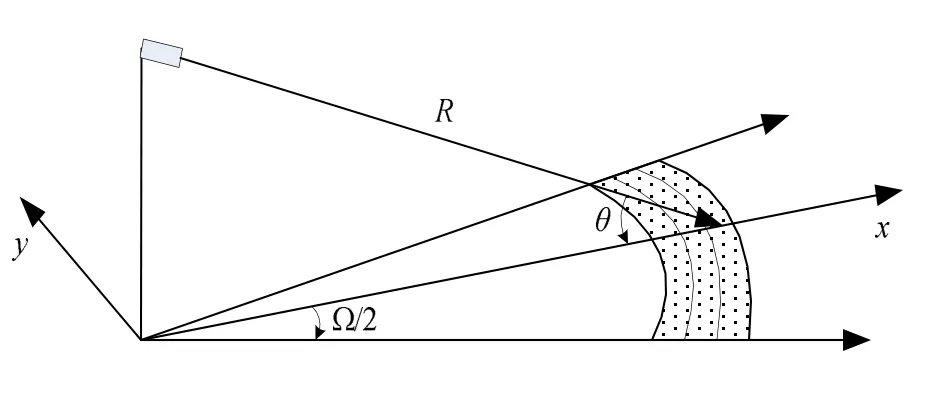
图1 收发合置主动声呐探测示意图
2 Jackson单基地散射模型
2.1粗糙海底的二维谱模型
海底散射通常包括海水与海底之间的粗糙界面散射和海底沉积层内的非均匀介质引起的体积散射,Jackson散射模型正是根据这一机理进行建模,认为海底散射强度为海底界面不平整性散射强度和海底沉积层体积散射强度之和。该模型假定海底界面起伏为各向同性、二维的高斯随机过程,海底沉积物在入射声波能够到达的深度内为均匀无分层的单一物质,不考虑其弹性和粘滞性的影响,沉积物性质用以下参数来描述:密度、声速、声吸收系数。
根据上述假设,海底界面的不平整性可用二维高度谱的概念进行描述[11,12]:
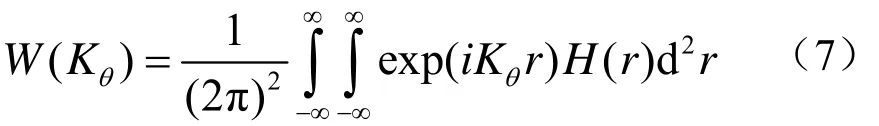
式中,W(Kθ)即为界面的二维高度谱密度,表示海底二维平面的起伏程度,H(r)为高度随机分布函数h(r)的自相关函数。在高度分布为各向同性高斯随机过程的假设前提下可求得:
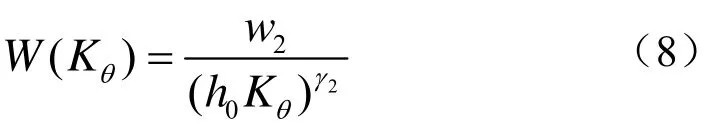

2.2模型参数
Jackson单基地散射模型中用到的海底环境参数见表1。

表1 Jackson单基地散射模型输入参数
一般情况下,上述海底底质参数是未知的,需要通过实际测量才能得到。Mourad和Jackson研究了上述参数和沉积物颗粒大小的对数值Mz间的经验性关系,以便于在以上参数未知情况下由Mz进行估算。其中,
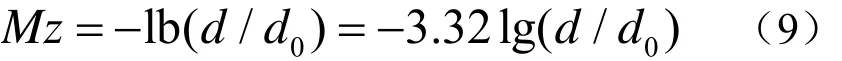
式中:d为沉积物颗粒大小的均值;d0为参考长度,通常为1 mm。当1≤Mz≤ 9时,上述六个参数可以通过Mz来估算,其具体关系式可参见文献[13]。
2.3反向散射强度计算
海底反向散射强度Sb(θ)可以用反向散射截面的分贝形式进行定义,Jackson散射模型中将反向散射截面分成两部分:
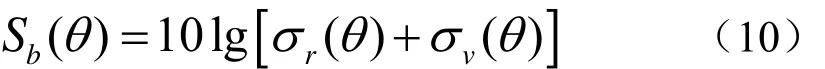
其中:σr(θ)为由粗糙界面及沉积物体积散射效应引起的单位面积对应无量纲的散射截面;σv(θ)是粗糙界面及沉积物体积散射效应引起的单位立体角对应无量纲的散射截面。具体计算公式可参见文献[13]。
3 海底混响建模与仿真计算
3.1海底混响模型
在1.2节介绍的基于物理过程的K分布混响模型和第2节介绍的Jackson海底散射模型的基础上,本节将给出一种基于物理散射的单基地海底混响仿真方法,该方法基于单元散射模型,具体做法是:将声呐波束覆盖的海底散射区域按一定距离间隔划分为不同的散射单元,单元内的散射体数目与单元的面积成正比、尺寸服从均值为μ的指数分布,参数μ与海底的散射强度有关,可以由Jackson散射模型计算得到,最终得到的混响信号为声呐照射区域内各元散射信号的迭加,其包络近似服从K分布。
为了简化分析,使模型易于数学表达和工程实现,在不影响模型精度的前提下,对模型做出以下合理假设:本文主要考虑近距离的海底混响干扰,因此不考虑海面的散射和多途效应;不考虑海底各散射体和单元间的多次散射;只考虑基阵指向角覆盖范围内的海底区域;海水均匀、等声速,声信号都是沿直线传播。
图1所示的单基地声呐主动探测示意图中:H为海底深度,Ω为发射波束束宽,θ为基阵法线方向与海底的掠射角,为第i个散射单元到接收点的距离,则发射信号s(t)经第i个散射单元散射后的双程传播时延为:

其中,c为海水中的声速。为了简化计算,本文对散射单元按照等时间间隔的原则进行划分,为了保证计算结果的可靠性,本文取时间间隔Δt的最大限度小于海底混响的时间相关半径,对于CW等窄带信号,其混响的时间相关半径约等于信号的脉宽T,则:

而对于LFM等宽带信号,混响的时间相关半径与信号带宽B成反比,即:


将要模拟海底的海底散射区域划分为N−1个散射单元,标号分别为D1, D2LDN −1,每块区域的形状为一个开角为Ψ的扇形圆环,其面积可以根据下式进行计算:

假设单位面积的海底散射体个数为β,则对应的第i个散射单元Di的散射体数目为:
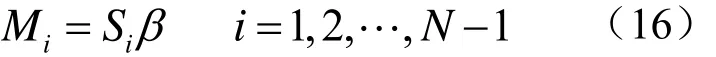
由于时间间隔Δt很小,D1, D2LDN −1的厚度很薄,因此可以认为在此区域内的所有散射体到接收换能器的距离相等,记为Ri,根据几何关系,可以得到:
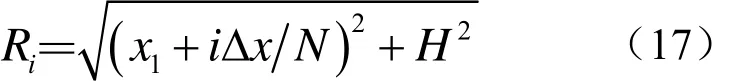
这样,在t时刻基阵接收到的第i个散射单元的散射信号可以表示为:

而最终得到的混响信号则可以记为:

其中,iτ为第i个散射单元中所有散射体的回波时延,可以由下式进行计算:
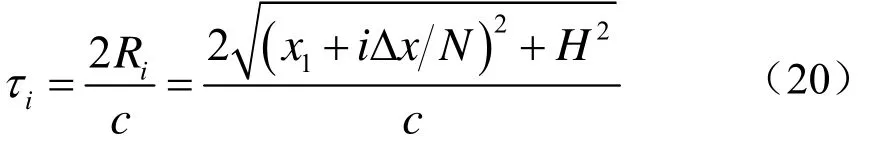
式中,ijϕ为第i个散射单元中第j个散射体的回波相位,Aij为其回波幅度,对于固定的i,相位ijϕ服从0~2π的均匀分布,幅度Aij服从均值为iμ的指数分布,总的混响信号的包络服从K分布。
考虑到声波在传播过程中受几何扩展、海水声吸收以及海底反向散射等因素的影响,第i个散射单元中iμ的取值可以由下式进行计算:


3.2仿真结果及分析
仿真参数设置:声呐基阵为收发合置18元水平线阵,阵元间距为0.07 m,发射波束束宽Ω=4°,基阵距海底深度H=20 m,海底为细砂底质,发射信号为7~14 kHz的LFM,脉宽T=5 ms,采样率fs=20 kHz,声速c=1 500 m/s,单位面积的海底散射体个数β=100,散射单元间的时间间隔Δt=1/2B,仿真的距离(斜距)范围为[25 m,100 m]。图2为仿真得到的海底混响时间序列波形及其频谱。若发射信号采用10 kHz的CW信号,散射单元间的时间间隔取Δt=T/2,其它条件不变,仿真得到的CW信号海底混响时间序列波形及其频谱如图3所示。
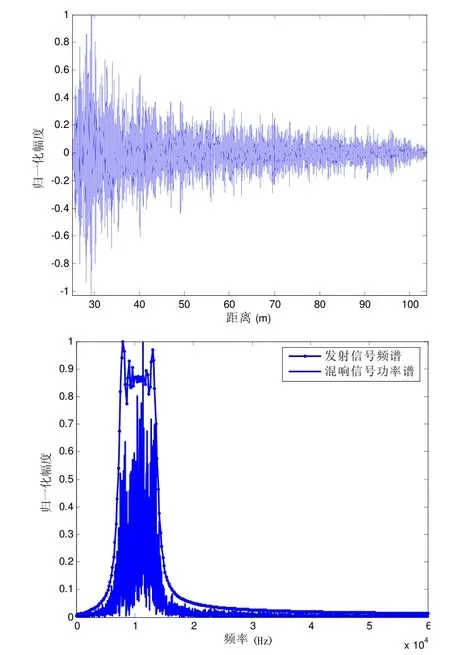
图2 LFM海底混响仿真信号及其频谱图

图3 CW海底混响仿真信号及其频谱图
从图2和3可以看出,仿真得到的混响信号幅度随距离呈指数衰减,与发射信号的频谱相比,混响信号的功率谱具有一定的扩展性,仿真结果与理论分析结果一致。
为了进一步验证本文模型的有效性,有必要对仿真数据的统计特性进行考察,检验仿真信号包络的概率密度是否满足K分布特性。图4给出了前述LFM信号和CW信号仿真混响序列包络的概率密度统计结果。从图中可以看出,两种情况下,仿真得到的混响信号包络均逼近于K分布,达到了预期的仿真目的。值得注意的是,LFM混响信号的统计结果比CW混响信号的统计结果更趋近于K分布,这主要是由于LFM信号的距离分辨率远高于CW信号,造成单个散射单元内的有效散射体数目减少,这也再次证实了1.1节中所提的随着系统空时分辨率的提高,混响的统计特性将趋于非瑞利分布这一结论。
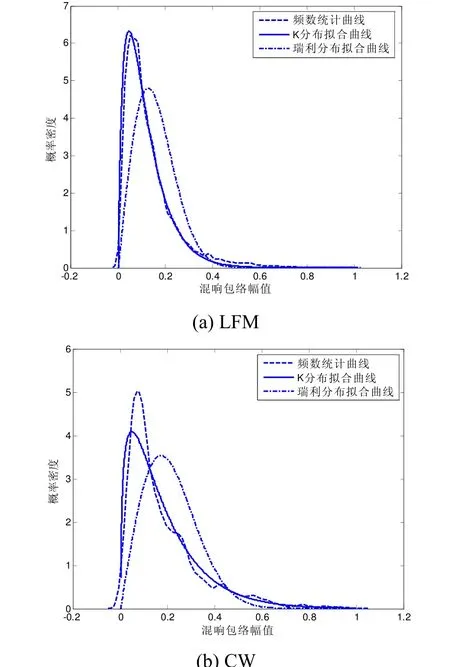
图4 海底混响仿真数据统计分布拟合图
4 结论
海底混响是主动声呐特别是探测沉底及掩埋小目标的主要干扰,其统计特性一般呈现较强的非瑞利性。目前的海底混响数值仿真方法一般都采用统计模型直接产生,尽管简单便利,但却失去了物理意义,没有将模型本身与声呐设备的各项物理参数和海底地声参数直接联系起来,无法在实验室条件下利用仿真数据开展更精确有效的探测效能分析。本文建立的基于物理散射的单基地海底混响仿真模型将混响统计特性与声呐的波束宽度、带宽、频率、掠射角等系统参数和散射体尺寸、散射强度、分布密度等环境参数联系起来,同时兼顾了海底混响的统计特性和物理形成机制,具有较高的仿真精度和实用价值,可以为海底目标探测的抗混响信号处理研究提供数据支撑,仿真结果验证了本文模型的有效性。
参考文献:
[1] 孙文俊. 主动声呐混响模型与抗混响信号处理[D]. 西安:西北工业大学, 2006.
[2] JAKEMAN E,PUSEY P N.A model for non-rayleigh sea echo [J].IEEE Transactions on Antennas and Propagation,1976,24(6):806-814.
[3] ABRAHAM D A.Statistical normalization of non-rayleigh reverberation [C].Proc. OCEANS’97 conf.,1997:500-505.[4] ABRAHAM D A.Modeling non-rayleigh reverberation [R].SR-266,SACLANT Und. Res. Cen.,1997.
[5] ABRAHAM D A.Choosing a non-rayleigh reverberation model [C].Proc. OCEANS’99 conf.,1999:284-288.
[6] ABRAHAM D A,LYONS P A.Novel physical interpretations of K-distributed reverberation [J].IEEE J. Oceanic Eng.,2002,27:800-813.
[7] ABRAHAM D A.Signal excess in K-distributed reverberation [J].IEEE J. Oceanic Eng.,2003,28(3):526-536.
[8] ABRAHAM D A,LYONS P A.Exponential scattering and K-distributed reverberation [C].Proc. OCEANS’01 conf.,2001:1622-1628.
[9] ABRAHAM D A,LYONS P A.Simulation of non-rayleigh reverberation and clutter [J].IEEE J. Oceanic Eng.,2004,29(2):347-362.
[10] ABRAHAM D A,LYONS P A.Reverberation envelop statistics and their dependence on sonar bandwidth and scattering patch size [J].IEEE J. Oceanic Eng.,2004,29(1):126-137.
[11] WILLIAMS K L,JACKSON D R.Bistatic bottom scattering:model,experiments,and model/data comparison [J].JASA,1998,103(1):169-180.
[12] LYONS A P,ADDERSON A L.Acoustic scattering from the seafloor:Modeling and data comparison [J].JASA,1994,95(5):2441-2451.
[13] MOURAD P D,JACKSON D R.High frequency sonar equation models for bottom backscatter and forward loss [C].IEEE proceedings of OCEANS,1989:1168-1175.
