分布性目标解卷层析成像

魏善义邹丽娜李春晓

（1.第七一五研究所 声纳技术重点实验室，杭州，310023）（2.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州，310014）



分布性目标解卷层析成像

魏善义1邹丽娜1李春晓2

（1.第七一五研究所 声纳技术重点实验室，杭州，310023）（2.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州，310014）

摘要在水声反射层析中，声信号照射目标并从多个角度接收目标的散射信号，就得到了目标的大量一维投影数据，处理多个角度的投影数据可以重构目标情景密度的二维空间分布。论文通过脉冲压缩和Richardson-Lucy解卷算法处理多角度观察分布性目标得到的一维投影数据，提取精确的目标散射参数，再通过滤波反投影算法（FBP）重构目标二维空间分布，同时实现了一个分布性目标和多个点目标的像重构。

关键词Richardson-Lucy解卷；投影层析；滤波反投影算法；分布性目标

层析成像技术（CT，computed tomography）在医学中已经得到了广泛且深入的应用，该技术能够通过对一个三维散射体在多个角度上获取的多组一维投影数据的处理，得到该三维散射体的横断面视图。这项技术在诊断医学中具有革命性的意义，因为它可以让医学专家在不伤害人体的情况下观察病人的内部器官细节。层析成像技术在其他领域也有广泛的应用，例如雷达、声呐、射电天文学、地球物理、无损检测和结构材料分析等。

本文将主要讨论层析成像技术在水声声呐成像领域中的应用。在海洋中存在各种各样的散射体，包括水面船只、潜艇和鱼群等，本文将感兴趣区域的所有散射体看作是“情景”，包括分布性目标和点目标，在情景被有效照射的前提下，进行多角度观察，通过对多组投影数据的处理，重构出情景的像。将海洋观测和目标探测构筑在一个框架中，实现分布性目标成像是很有意义的。

1　回波信号建模

假设一个理想情况：目标之间无遮挡、目标无声吸收，并且可以离散化处理。情景位于(x , y)域，在有效照射和有效接收的前提下，接收水听器从各个角度接收到情景的散射信号，可看作情景信号按照Radon变换规则变换到(s , θ)域，每个角度的水听器对应维度θ，接收信号序列对应维度t=2(R0+s)/ c 。

一个函数w(x , y)的Radon变换[1]描述为函数w(x , y)在与x轴夹角为θ的方向上位置s处沿s⊥轴方向的线积分，用函数g(s , θ)表示。g(s , θ)是函数w(x , y)在角度θ上的一维投影。

见图1，从θj角度、在ti时刻观察分布性目标w(x , y)，得到的接收信号是目标中波前（直线xcosθj+ysin θj= si）所在的那部分散射体回波信号的叠加。可以用一个线积分表示：

图1　平台-目标几何平面图

由于坐标轴发生旋转，变量之间存在如下关系，

从而，接收到的回波信号可以表示为：

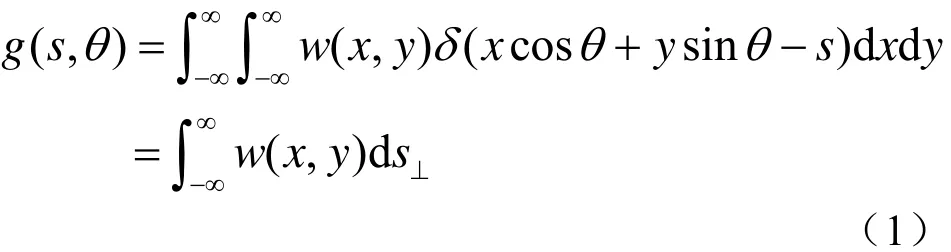
对于吸收层析数据来说，观察角度θ的范围仅需从0到π，而从π到2π角度范围观察目标提供的信息是冗余的，因为p(s ,θ)=p (− s ,θ+π)，这也体现了Radon变换的对称性质。对于反射层析数据来讲，遮挡会导致目标的某一部分在声影区而不能被观察到，即从θ角度不能得到完整数据，需要从相反方向θ+π来弥补数据，所以观察角度θ的范围应从0到2π。本文主要研究反射数据。

2　解卷算法

输入s(y)经过滤波器h(x | y)并加入噪声n(x)得到输出信号r(x)，可以用公式表示为：

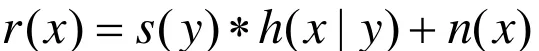
这是一个卷积过程，若已知r(x)和h(x | y)，估计s(y)，就称之为解卷。

在处理接收信号时，经常面对解卷、去模糊问题，解卷算法包括Wiener滤波、clean算法和Richardson-Lucy算法等。Richardson-Lucy算法是一个常用的迭代解卷算法，RL算法在得到清晰像的同时也存在一些不足，一是振铃效应，二是噪声放大。目前已有很多方法解决这些问题[2-3]。

信息理论熵方法的kullback 最小鉴别函数[4]是对两个概率密度函数p和q之间“距离”的度量：

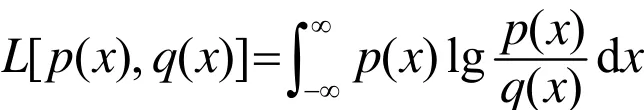
使鉴别函数（目标函数）最小，可以给出RL算法的推导。在已知r(x)和h(x | y)时，解卷s(y)要满足

最终，RL解卷算法对s(y)的估计为迭代表达式：

其中，i为迭代次数。令s0(y)= s (y)开始迭代。随着迭代次数的增加，图像会更加清晰，同时噪声也被放大，迭代次数在二者之间取折衷。

将解卷算法用于层析成像，在成像过程前期，对互脉冲压缩和自脉冲压缩进行解卷，称为信号解卷，如（2）式：

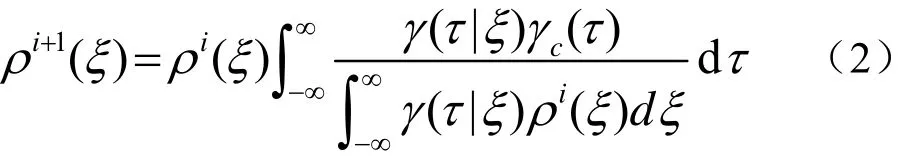
其中，ρ(ξ)为情景密度，γ(τ|ξ)为自脉冲压缩函数，γc(τ)为互脉冲压缩函数。

信号解卷可去除信号自身带来的模糊，提高目标的距离分辨力。良好的解卷数据对后续的像层析重构具有重要意义。

3　层析方法

将多组低维投影组合成一个高维像的技术称为层析技术，层析同时也可以用来描述将一些低质量的像增强为高质量像的技术。很多数据可以用来做层析处理，包括吸收、辐射、散射和漫射等。

3.1滤波反投影算法（FBP）

在得到观察信息g(s , )θ之后，像重构问题就等效成寻求g(s , )θ的逆Radon变换的问题。这样的方法包括滤波反投影算法、卷积反投影算法、二维傅里叶重构算法等。算法的选取是像重构的核心，对重构的像质量影响较大。本文采用滤波反投影算法[5]。

对接收信号傅里叶变换，

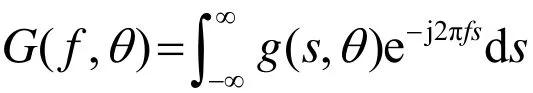
将（1）式代入其中，得

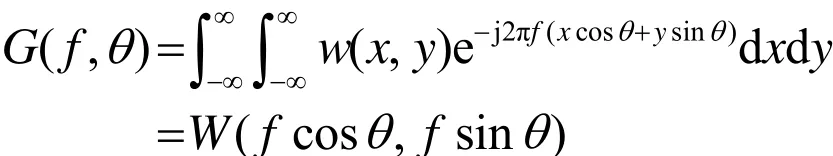
将分布性目标情景w(x , y)二维逆傅里叶变换并且变换到极坐标系下，得到FBP算法核心公式：

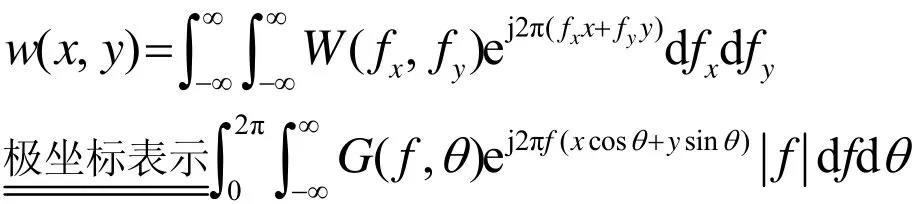
其中，fx= fcosθ ,fy=f sinθ。可以看出滤波反投影算法的计算过程分为两步，第一步是将投影数据g(s ,θ)通过频响为|f|的滤波器，第二步反投影生成w(x , y)。计算流程如图2所示。

在实际情况中，观察角度间隔不可能取到无限小，甚至可能很大，接收信号在角度维上是一组离散数据，需要采用合理的插值方法。不同的插值方法导致的内插误差会直接影响到成像的质量，插值方法包括最近邻插值、线性插值、样条插值等。

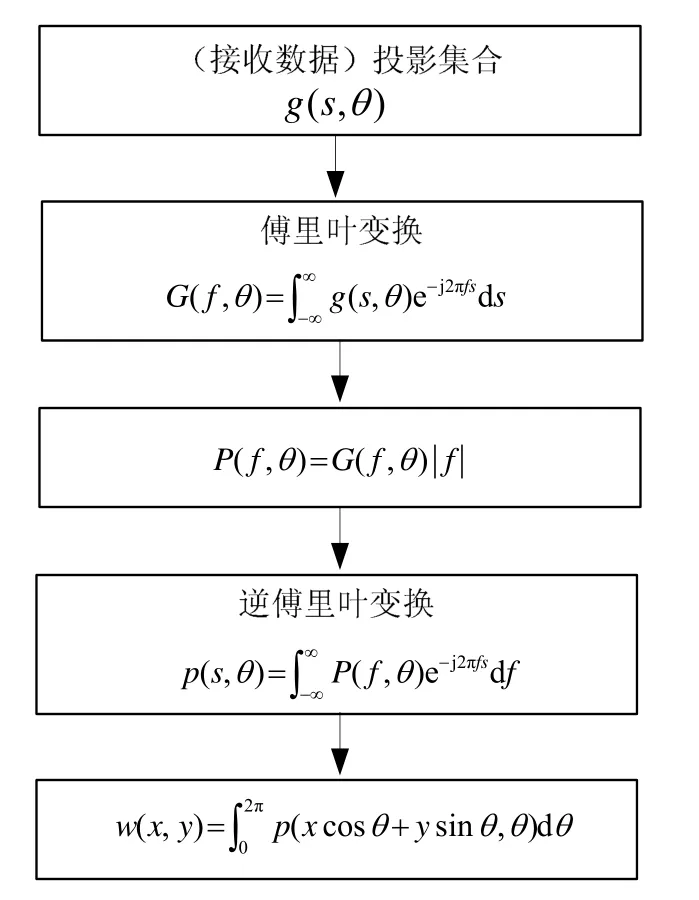
图2　滤波反投影算法流程

3.2曲率拟合

滤波反投影算法完成了将接收到的(s ,θ)域信号重构(x , y)域情景像的任务，此过程需要注意的是，(s ,θ)域曲线的正规性对成像效果的影响较大，而散射信号受到信道不确实性、声速剖面引起的声线弯曲传播等因素影响，需要进行曲率拟合，将带有偏差的曲线拟合成正规的曲线。

4　多视成像仿真分析

针对海洋环境进行仿真，成像场景的几何模型和海洋声场环境如图3所示。成像区域水平半径为1 km，水听器围绕成像区域做圆周运动，每10°间隔采样一次，垂直方向上，目标和水听器都位于深度65 m处，声源发射声信号照亮成像区域，声能量经过目标时发生散射，接收水听器在各个角度方向将接收到目标散射信号。

图3　(a) 成像场景的几何模型

图3　(b) 声场环境参数

海洋水层深度135 m，声速剖面负梯度：1 521~ 1 508 m/s，密度1 g/cm3，声吸收0 dB/波长；沉积层厚度20 m，声速1 690 m/s，密度1.8 g/cm3，声吸收0.673 dB/波长；底层半空间声速1 800 m/s，密度2 g/cm3，声吸收0.8 dB/波长。

待成像的情景包括1个分布性目标和3个点目标，以观察中心为坐标原点，分布性目标一端为坐标原点，面向270°方向40 m长的长方体目标，如图3（a），仿真分布性目标散射信号时，将其离散成20个间隔Δx=2 m的点目标进行考虑；3个点目标的位置信息采用极坐标表示，参数见表1。

表1　散射体参数

分布性目标解卷层析成像可分为四步。首先，根据发射信号，对接收信号进行互脉冲压缩；第二步，信号解卷，去除信号自身带来的模糊问题；第三步，曲率拟合，均衡信道带来的不确实性等问题；最后，滤波反投影算法，重构分布性目标的像。流程如图4所示。

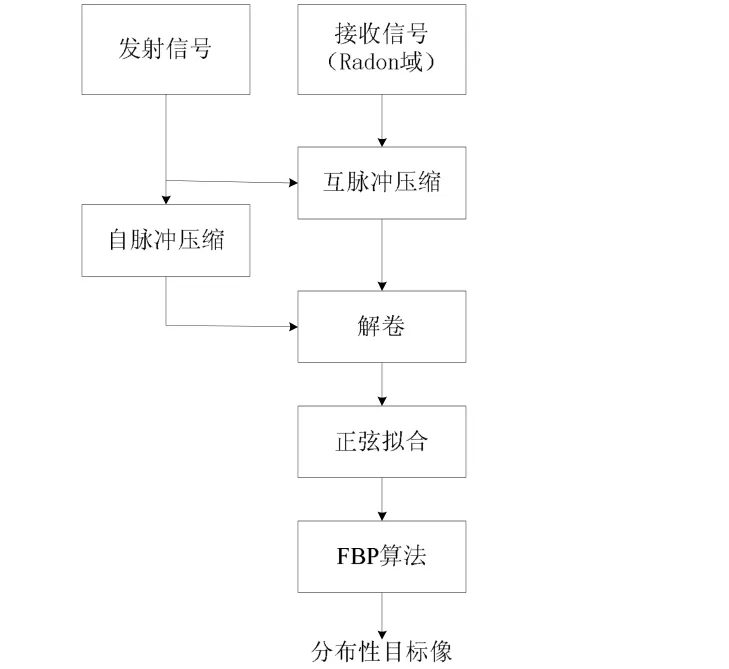
图4　分布性目标解卷层析成像流程

声源发射信号为300~800 Hz的线性调频信号，脉宽100 ms，经目标散射，应用kraken模型可以仿真出各水听器接收的散射信号，将接收信号归一化，图5所示。

图5　水听器接收的归一化散射信号

将接收到的36组散射信号，即(s ,θ)域数据，依次经过脉冲压缩、信号解卷（RL算法10次迭代解卷）和曲率拟合之后的结果如图6所示，横坐标为时间，纵坐标为观察角度的序号，至此我们已经得到了进行滤波反投影算法所必需的输入数据，即g(s , θ)。

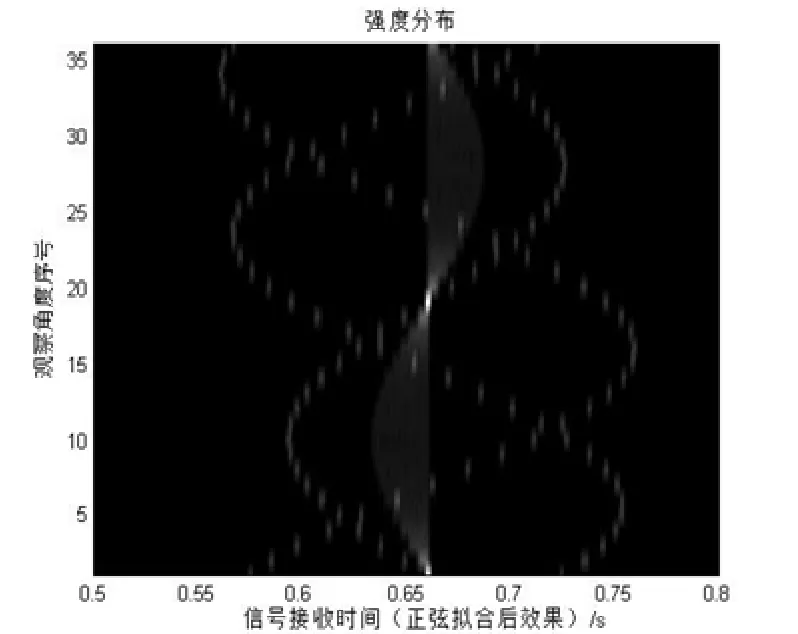
图6　依次经过脉冲压缩、信号解卷和正弦拟合后的结果

根据图2流程进行滤波反投影重构，重构情景的像如图7（a）所示。分布性目标由双向箭头指出，3个点目标由单向箭头指出。由于算法自身的原因，针对线性分布性目标时，在目标延伸方向会出现较高的“虚像”，但是分布性目标存在的区域强度更高，图7（b）给出了分布性目标延伸方向，即Y轴的强度分布图。图中3个点目标的位置分别为：（97.06,100.40）、（−126.70,76.41）、（0.19，−98.56），单位m。水平距离误差分别为：0.2687 m、2.7 m、3.5 m、1.4525 m，相对误差均低于2‰。分布性目标位置分布为从−0.94 m到40.74 m，与设定值0 m到40 m相吻合。

图7　（a） FBP算法重构分布性目标像

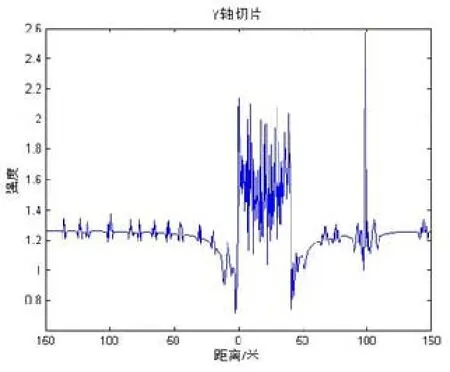
图7　（b） Y轴的强度分布图

5　结论及展望

5.1结论

本论文以滤波反投影算法为核心，将计算机层析技术应用到海洋波导分布性目标像形成工作中，通过仿真实现了对分布性目标和多个点目标的成像，并取得了较高的精确度。

5.2进一步展望

论文仿真中给出的是半径为1 km的观察区域，如果需要大面积观察，可以采用水声组网方式，实现水下分布式检测。如正六边形网络单元，每个观察区域单元可以设置六个观察角度（六组接收水听器），蔓延覆盖较大面积区域，如图8，这些观察节点可以由固定基站或是临时航空吊放声呐等组成。布防于战略敏感区域，实现对敏感区域的实时情景成像。

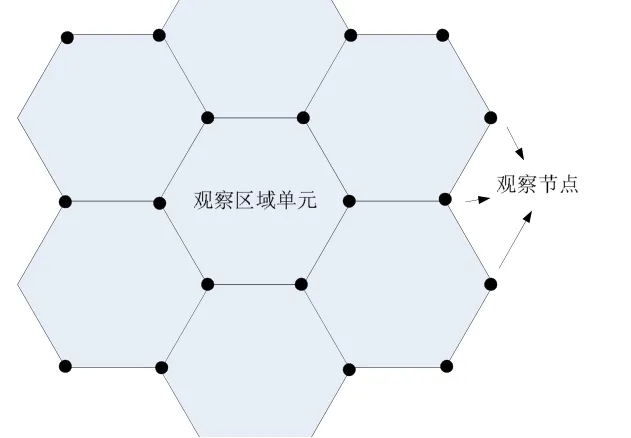
图8　大面积观察组网构想图

参考文献：

[1] RICHARD E BLAHUT. Theory of remote image formation[M]. London: Cambridge University Press, 2004.

[2] WU JIUNN LIN, CHANG CHIA-FENG. An improved richardson-lucy algorithm for single image deblurring using local extrema filtering[J]. IEEE International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), 2012.

[3] CUNHA A L. The nonsubsampled contourlet transform : theory, design, and applications[J]. IEEE Trans. on image Processing, 2006,15(10):3089-3101.

[4] THOMAS M COVER, JOY A. Thomas. elements of information theory[M]. New York: Wiley-Interscience, 2006.

[5] BRIAN G FERGUSON, RON J WYBER. Application of acoustic reflection tomography to sonar imaging[J], JASA, 2005, 117(5):2915-2928.