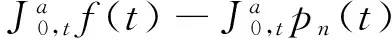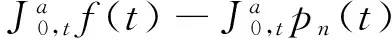Caputo型分数阶微积分求解及其误差估计

李瑾

(河南财政税务高等专科学校 信息工程系， 河南 郑州 451464)

Caputo型分数阶微积分求解及其误差估计

李瑾

(河南财政税务高等专科学校 信息工程系， 河南 郑州 451464)

研究Caputo 型分数阶微分函数的正解情况，考察其正解的唯一性问题，进而研究其数值求解的误差估计，所得结果拓展了Wyss的研究成果.

分数阶微积分; Caputo型； Chebyshev 多项式； 误差估计； 唯一性.

分数阶微积分在一些混沌领域，如在遗传数理得到了较为广泛的应用[1-3].然而，由于其应用上的非局部性，使得分数阶微积分数值计算较为复杂，进而导致发展较为缓慢[4].Diethelm[5]根据前人的研究成果[6-11]，给出了几种较为常见的分数阶微积分的数值算法，并提出了分数阶微积分的Gauss求解原理及算法.本文基于Sugiura等[12]的分数阶微积分Chebyshev 多项式数值算法模型，考察Wyss等[13]设计的Caputo 型分数阶微分函数的正解情况，进而研究其数值求解的误差估计.

1 分数阶积分及其拓展算法

Wyss和Chneider建构了分数阶积分函数，令φ(x)，ψ(x)为已知函数，所组成的偏微分方程为

为进一步研究高阶分数阶积分，Miyakoda拓展了Wyss的研究成果，建构基于Chebyshev多项式逼近的高阶分数阶积分[13].为此，令函数f(x)分数阶积分为

结合文献[3]的研究，对上述方程进行多项式逼近，可得到

T0(x)=1，T1(x)=x，Tn+1(x)=2xTn(x)-Tn-1(x).

结合式(4)，由方程(1)可得

为了进一步得出该多项式的算法，记pn为式(4)的n次多项式，于是有

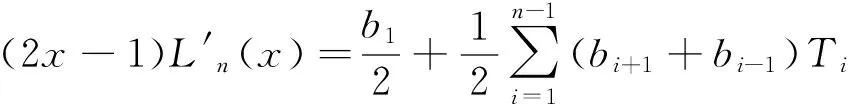
于是,可得到

由方程(9)中Ti(2x-1)(i=1，2，…，n)的系数，可以得到

所以，分数阶积分(1)的数值算法为

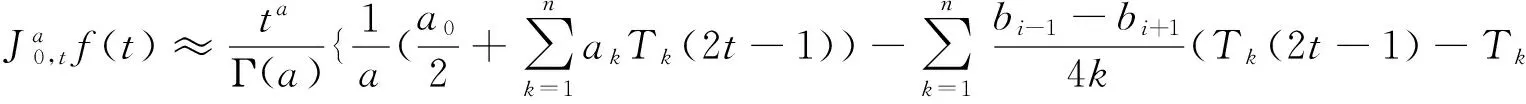
式(11)中:α>a，t∈[0，1]，ak，bk由方程(4)及方程(10)给出.

2 Caputo型分数阶微分的数值算法

首先，给出Caputo型分数阶导数的定义.令函数f(t)的Caputo型分数阶导数为

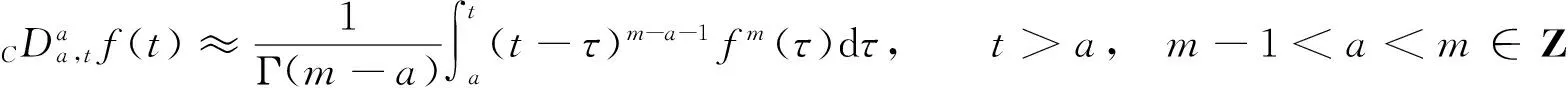
式(12)中:Γ(·)是Gamma函数.接下来，对该导数进行Chebyshev多项处理，可得

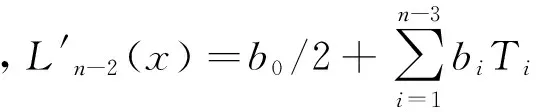
进而得到

为了进一步明确bi，将方程(16)～(18)整合,可得到

可以发现

式(18)中：k=1，2，…，n-2;bn-1=bn-2=0.于是,可得到Caputo型的分数阶导数的数值算法为

当前粮食的机械干燥方法主要包括热风干燥、真空干燥、微波干燥、太阳能干燥、热泵干燥、就仓干燥、红外辐射干燥以及热风——微波联合干燥等新型干燥技术，其中热风干燥技术依旧是应用较普遍的干燥技术[2]。为此，利用DHG-9240A型热风干燥试验装置进行试验，分析在不同温度、风速和物料薄层厚度条件下高水分小麦的热风干燥特性，并建立高水分小麦热风干燥数学模型，进而揭示高水分小麦的热风干燥规律和干燥机理，为高水分小麦热风干燥工艺建立及其设备研制提供理论依据。

式(19)中：α∈(1，2)，t∈[0，1]，而dk，bk分别由方程(17)，(18) 确定.

3 Caputo型分数阶微分方程解的唯一性问题

当t∈(0，+∞)，(0，∞)→R时，f(x)的a阶(a∈R+)分数阶积分为

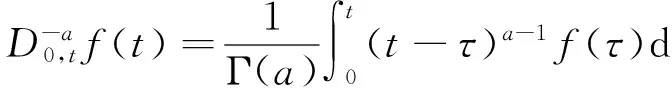
所以，其Caputo型分数阶导数则为

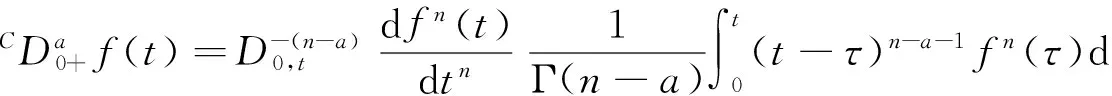
假设G(t，s)>0(t，s∈(0，1)为Green函数，于是，在g∈[0，1]，2≤a≤3，Caputo型分数阶导数微分方程为

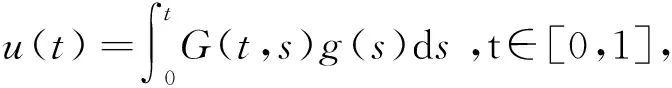
设P={x∈C[0，1]|x(t)≥0，t∈[0，1]}，所以P为Banach空间C的正规锥，于是提出如下假设.

假设1f(t，u，v)∶[0，1]×[0，∞)×[0，∞)→[0，∞)连续，且f(t，0，1)≠0.

假设2 当t∈[0，1]，v∈[0，∞)时，在u∈[0，+∞)区间，f(t，u，v)单调递增；当t∈[0，1]，u∈[0，+∞)时，在v∈[0，+∞)区间，f(t，u，v)单调递减；∀γ∈(0，1)，存在φ(γ)∈(γ，1)，使f(t，γu，γ-1)≥

φ(γ)f(t，u，v)，∀u，v∈[0，∞).于是，提出以下3点结论.

1) 存在r∈(0，1)及u0，v0∈Pw，使不等式rv0≤u0

上式中：w(t)=t，t∈[0，1].

2) 在P={x∈C[0，1]|f(x)≥0，x∈[0，1]}，Caputo分数阶微分方程具有唯一解u*.

3) ∀x0，y0∈P，构造迭代序列

上式中：n=1，2，….

当n→∞时，xn(t)→u*(t)，yn(t)→u*(t)成立.

4 误差分析

由于前述的Chebyshev多项式pn(x)具有解的有界性和一致性，所以有

于是，在积分空间Cr上，Chebyshev多项式分数阶积分f(x)的数值算法具有误差估计为

所以，在积分空间Cr上，Chebyshev多项式分数阶积分f(x)的数值算法具有的误差估计满足

于是，En(t)=f(t)-pn(t)=An+1(t)Bn(t)，又由于Chebyshev多项式f(x)的一致有界性，所以有

注 上述结论中o的含义为n→+∞时，Chebyshev多项式f(x)数值算法误差的收敛速率.

[1] PODLUBNY I.Fractional differential equations， mathematics in science and engineering[M].New York:Academic Press,1996:120-125.

[2] MILLER K S,Ross B.An introduction to the fractional calculus and fractional differential equations [M].New York:John Wiley,1998:76-91.

[3] HIEBER M.Laplace transforms and α-time integrated semigroups[J].Forum Math,1991,120(3):595-612.

[4] 徐明瑜，谭文长.中间过程、临界现象：分数阶算子理论、方法、进展及其在现代力学中的应用[J].中国科学(G辑)，2006，36(3):198-229.

[5] DIETHELM K.An improvement of a nonclassical numerical method for the computation of fractional derivatives[J].Numer Algor，2009，131(1):209-254.

[6] SUGIURA H，HASEGAWA T.Quadrature rule for Abel′s equations: Uniformly approximating fractional derivatives[J].Comput Appl Math，2009，223(1):460-471.

[7] FOX C.The G and H functions as summertrical Fourier kernels[J].Trans Amer Math Soc,1961(98):396-410.

[8] ELLIOTT D.ELLIOTT Truncation errors in two Chebyshev series approximations [J].Math Compute,1965(19):234-248.

[9] FUJITA Y. Fujita Cauchy problems of fractional order and stable processes[J]. Japan J Appl Math, 1990, 7(3): 459-476.

[10] FUJITA Y.Integro differential equation which interpolates the wave equation[J].Osaka J Math,1990,116(27):797-804.

[11] YCAN L,AGTTAWAL O P.A numerical scheme for dynamic systems containing fractional derivatives[J].ASME J Vibr Acoust,2002，124(2):321-324.

[12] HASEGAVA T,SUGIURA H.Uniform approximation to fractional derivatives of functions of algebraic; singularity[J].Compute Appl Math,2009，228(1):247-253.

[13] SCHNEIDER W R，WYSS W.Fractional diffusion and wave equations[J].J Math Phys，1989,134(30):129-139.

[14] FUJITA Y.Energy inequalities for interop-partial differential equations with Riemann Lowville integrals[J].SIAM J Math Anal，1992(23):1179-1201.

[15] BAI Zhanbing.Eigenvalue intervals for a class of fractional boundary value problem[J].Computers and Mathematics with Applications，2012,64(10):3248-3261.

(责任编辑： 陈志贤 英文审校： 吴逢铁)

Algorithm and Error Estimate on the Fractional Differential Equation With Caputo Derivative

LI Jin

(Department of Information Technology, Henan Finance and Taxation College, Zhengzhou 451464, China)

The development speed of the reactional differential equation is slow due to the application nonlocality and the calculative complexity. In this paper, we will discuss the positive solution to the fractional differential equation with Caputo derivative based on the current research. Then we also study the uniqueness of the solution and discern the deviation comparing with numerical solution. The paper expands Wyss′ research and conclusion.

fractional differential equation; Caputo derivative； Chebyshv polynomial; error estimate； uniqueness

1000-5013(2015)06-0721-05

10.11830/ISSN.1000-5013.2015.06.0721

2015-10-08

李瑾(1961-)，女，副教授，主要从事微积分及经济数学的研究.E-mail:396319685@qq.com.

河南省2014年软科学研究计划项目(142400411076)

O 155

A