A-收敛与几乎处处收敛
2015-02-21鲍玲鑫施慧华
鲍玲鑫, 施慧华
(1. 福建农林大学 计算机与信息学院, 福建 福州 350002;2. 华侨大学 数学科学学院, 福建 泉州 362021)
A-收敛与几乎处处收敛
鲍玲鑫1, 施慧华2
(1. 福建农林大学 计算机与信息学院, 福建 福州 350002;2. 华侨大学 数学科学学院, 福建 泉州 362021)
设A≡(ai)∞i=1⊂S+,其中,S+表示1单位球面上的所有正向量构成的集合.Banach空间X中的序列(xn)称为A-收敛于x∈X,是指对任意的ε>0,limi→∞ai,χA(ε)=0,其中,A(ε)={n∈N∶‖xn-x‖≥ε}.用两种不同的收敛方式刻画A-收敛,即证明对任意A≡(ai)∞i=1⊂S+,存在一个N上的理想IA,以及一族极端有限可加概率测度Pext(IA),使A-收敛且理想IA-收敛和测度Pext(IA)-收敛互为等价.此外,证明A-收敛为测度Pext(IA)-几乎处处收敛的充分必要条件是该A-收敛为非退化的.
统计收敛; 理想收敛; 几乎处处收敛; 极端测度; Banach空间.

1 A-收敛和理想收敛与极端测度收敛
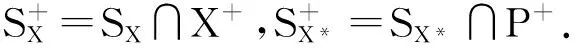
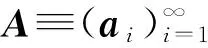
注释1 1) 若令定义中A=(ei), 则A-收敛等价于经典的序列收敛.
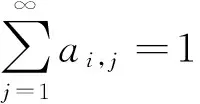

记MA={x*∘χ(·)∶x*∈∂pA(e)},则文献[9]证明了MA⊂P(N,2N),其中,P(N,2N)表示定义在可测空间(N,2N)上所有有限可加概率测度构成的集合.
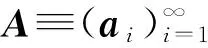
若I⊂2N满足:1) 任意A,B∈I,A∪B∈I;2) 任意的A∈I及B⊆A,B∈I,则称I为N上的一个理想.如果理想I还满足:I≠Ø(N∉I,包含所有单点集),则称I为非平凡(真,统计型)理想.对于上述定义的连续半范数pA,令IA={A∈2N∶pA(χA)=0},则容易验证IA为N上的一个非平凡的真理想.IA为统计型理想的充分必要条件参见文献[9]的定理4.2.定义

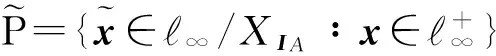

设f是定义在X上的连续凸函数,则f在点x∈X的次微分映射∂f(∶X→2X*)定义为
∂f(x)={x*∈X*∶f(x+y)-f(x)≥x*,y,对任意的y∈X}.
性质1是经典的[10].
性质1 设p是定义在X上连续的Minkowski泛函,则对任意给定x∈X,有1) ∂f(x)是非空w*-紧凸集;2)x*∈∂f(x),当且仅当x*≤p,且x*,x=p(x).
定理2 1) 对任意的A∈2N,pA(χA)=0,当且仅当qA(χA)=0.
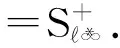
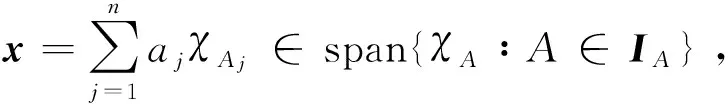
2) 根据文献[8]的引理2.9可知,qA(e)=dist(e,XIA)=1=‖e‖.另外,不难验证qA(x)≤‖x‖对一切x∈∞成立.根据性质1中2)可知,∂qA(e)⊂∂‖e‖.∂‖e‖为文献[9]中命题2.2的一部分.
基于此,只需找到一个x*∈∂qA(e)使x*,x)=qA(x,便可以保证第一个“=”成立.对于上述在商空间∞/XIA中,利用Hahn-Banach定理可知,存在使‖‖=1,并且‖‖.根据经典定理可知,存在唯一的使‖‖=‖x*‖及对所有的y∈∞成立.特别的,

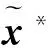
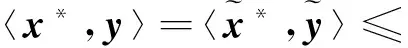
再根据性质1中2)可知,x*∈∂qA(e).
对于第二个“=”,注意到性质1中1),∂qA(e)是一个非空的w*-紧凸集.从而根据Krein-Milman定理得到第二个等号成立.
注释2 由定理2中2)可知,∂qA(e)∘χ(·)⊂∂‖e‖∘χ(·)=P(N,2N).定义
P(N,2N,IA)={μ∈P(N,2N)∶μ(A)=0对所有的A∈IA}.
根据定理2中1),3),在文献[8]定理2.3的意义下,有P(N,2N,IA)≅∂qA(e). 即有P(N,2N,IA)=∂qA(e)∘χ(·).
令Pext(N,2N,IA)=ext ∂qA(e)∘χ(·).下文中分别用P(IA)和Pext(IA)表示P(N,2N,IA)和Pext(N,2N,IA).
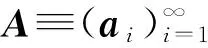
证明 1)⇔2) 即为定理1.
2)⇔3) 由性质1,定理2以及IA的定义即可验证.
3)⇔4) 注意到注释2的P(IA)≅∂qA(e)即可得到.
4)⇔5) 只需利用定理2中3)即可验证.
2 A-收敛与几乎处处收敛
作为文献[12]定理1.5的特殊情形,有如下结论成立.
定理4 设x*∈∂qA(e),则x*∈ext ∂qA(e)当且仅当x*为∞上的保正交不变的泛函,即对任意的x=(x(n)),y=(y(n))∈∞满足:xy=(x(n)y(n))=0,x*,xy=0.
基于此,可以得到如下结论.

证明 设x*∈ext ∂qA(e),若x*,en=0对一切n∈N成立,则此时有若存在某个n0∈N使x*,en0≠0,根据定理4可知,x*,en0x*,χN{n0}=0.从而有x*,en0=1及x*,χN{n0}=0.如果x*∈1,且注意到定理2中2),可得x*=en0.下面只需证明x*∈1.因为所以存在正分解其中1∩P+及从而有
以及
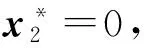
注释3 对任意的x*∈ext ∂qA(e),x*要么是纯连续,要么是w*-序列连续的.从而对任意的μ∈Pext(IA),μ要么是可数可加测度,要么是纯有限可加测度.其中,相关概念与性质可以参考文献[13].
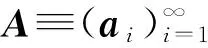
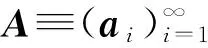
这里称A-收敛为退化的原因是它等价于由有限个退化的测度定义的收敛.称A∈2N为Pext(IA)-零测集是指对任意的μ∈Pext(IA)都有μ(A)=0.
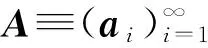
注释4 由定理3及定义3可知,序列(xn)⊂X为Pext(IA)-几乎处处收敛于x总是意味着(xn)A-收敛于x.
下面给出A-收敛为几乎处处收敛的一个充分必要条件.
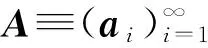
证明 充分性是显然的.因为如果A-收敛是退化的,根据定理5可知,存在有限个正整数A≡{n1,n2,…,nk}使Pext(IA)={en1∘χ(·),en2∘χ(·),…,enk∘χ(·)}.对任意的x0∈X{0},定义序列xn=x0,n∈A;=0,n∈NA.则不难验证,(xn)A-收敛于x0,但不会Pext(IA)-几乎处处收敛于x0.这是一个矛盾.
往证必要性.设(xn)A-收敛于x,且令
C0={n∈N∶‖x0-x‖≥1},Ck={n∈N∶2-k<‖xn-x‖≤2-(k-1)},(k=1,2,…).

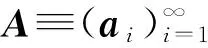
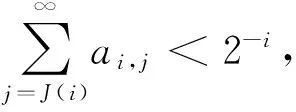

下面证明上述3个断言.
1) 对任意i≥m0,都存在唯一的k(i)∈N,使mk(i)≤i
注意到i→∞时,k(i)→∞.根据定理2中1),3)可知
pA(χB)=0=qA(χB)=sup{(x*,χB)∶x*∈ext ∂qA(e)}.
即得到B为Pext(IA)-零测集.
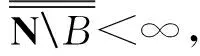

推论1 经典统计收敛、A-统计收敛(包括lacunary-统计收敛和λ-统计收敛)在统计测度意义下都是几乎处处收敛的.
[1] FAST H.Sur la convergence statistique[J].Colloq Math,1951,2:241-244.
[2] STEINHAUS H.Sur la convergence ordinaire et la convergence asymptotique[J].Colloq Math,1951,2:73-74.
[3] CONNOR J.On strong matrix summability with respect to a modulus and statistical convergence[J].Canad Math Bull,1989,32(2):194-198.
[4] FRIDY J,ORHAN C.Lacunary statistical convergence[J].Pacific J Math,1993,160(1):43-51.
[5] KOSTYRKO P,SALAT T,WILCZYNSKI W.I-convergence[J].Real Anal Exchange,2000/2001,26(2):669-689.
[6] CHENG Lixin,LIN Guochen,LAN Yongyi.Measure theory of statistical convergence[J].Sci China Ser A,2008,51(12):2285-2303.
[7] CHENG Lixin,LIN Guochen,SHI Huihua.On real-valued measures of statistical type and their applications to statistical convergence[J].Mathematical and Computer Modelling,2009,50:116-122.
[8] BAO Lingxin,CHENG Lixin.On statistical measure theory[J]. J Math Anal Appl,2013,407:413-424.
[9] BAO Lingxin,LIN Lihua.On convergences[J].Journal of Mathmatical Study,2013,46:116-125.
[10] CHENG Lixin,SHI Shuzhong,LEE E.Generic Frechet differentiability of convex functions on non-Asplund spaces[J].J Math Anal Appl,1997,214(2):367-377.
[11] HOLMES R B.Geometric functional analysis and its appications[M].New York:Sringer-Verlag,1975:123-124,129-130.
[12] BAO Lingxin.Ideal convergence and almost usual convergence[EB/OL].[2015-06-01].http://advmath.pku.edu.cn/CN/10.11845/sxjz.2015061b.
[13] CHENG Lixin,SHI Huihua.A functional characterization of measures and the Banach-Ulam problem[J].J Math Anal Appl,2011,374:558-565.
(责任编辑: 钱筠 英文审校: 黄心中)
OnA-Convergence and Almost Usual Convergence
BAO Lingxin1, SHI Huihua2
(1. School of Computer and Information, Fujian Agriculture and Forestry University, Fuzhou 350002, China; 2. School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China)
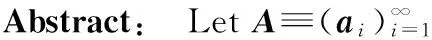
statistical convergence; ideal convergence; almost usual convergence; extreme measures; Banach space
1000-5013(2015)06-0726-05
10.11830/ISSN.1000-5013.2015.06.0726
2015-04-03
鲍玲鑫(1982-),男,讲师,博士,主要从事基础数学泛函分析、Banach空间几何的研究.E-mail:bolingxmu@sina.com.
国家自然科学基金专项数学天元基金资助项目(11426064, 11426061); 国家自然科学基金青年基金资助项目(11401227, 11501108); 福建省自然科学基金资助项目(2015J01579)
O 177.2
A
