三轴压缩岩石应变软化及渗透率演化的试验和数值模拟

张春会,赵全胜,王来贵,赵 娜,于永江

(1.河北科技大学建筑工程学院,河北石家庄 050018;2.辽宁工程技术大学力学与工程学院,辽宁阜新 123000)



三轴压缩岩石应变软化及渗透率演化的试验和数值模拟

张春会1,2,赵全胜1,王来贵2,赵 娜2,于永江2

(1.河北科技大学建筑工程学院,河北石家庄 050018;2.辽宁工程技术大学力学与工程学院,辽宁阜新 123000)

摘 要:三轴压缩下岩石峰后应变软化行为及渗透率演化规律是岩石工程稳定性分析的基础。取新疆巴里坤砂岩样在室内开展了三轴压缩试验和三轴渗流试验,获得了不同围压下巴里坤砂岩的全程应力应变曲线、体积应变与渗透率关系曲线。试验结果表明:随着围压增加,岩石峰后残余强度增加,体积扩容和脆性减弱;随着轴向应变增加,岩石先发生弹性压缩,空隙空间减小,渗透率降低;当应力达到屈服强度,岩石内裂隙开始扩展,渗透率降低速率趋缓;在峰值应力后,岩样破坏,裂隙扩展加速,并伴有新裂隙的萌生,岩样渗透率开始快速增长,岩样的渗透率呈“V”型变化。提出了描述围压对岩石峰后脆性影响的新参数,即脆性模量系数,围压与脆性模量系数之间服从负指数关系。基于脆性模量系数、强度退化指数和扩容指数,建立了考虑围压影响的岩石应变软化模型。在分析体积应变与岩石渗透率之间关系基础上,建立了基于体积应变增透率的岩石渗透率演化模型。在FLAC下模拟了巴里坤砂岩不同围压下的应变软化行为和渗透率演化过程,结果表明:岩石应变软化模型能很好地模拟围压对岩石残余强度、体积扩容和峰后脆性的影响;所示模型能较好地模拟围压和剪胀对岩石渗透率的影响;岩样峰后内部出现了明显的剪切破坏带,剪切破坏带与大主应力的夹角随着围压的增加而增大。在剪切破坏带内单元的渗透率显著增长,最后形成了一个流动通道。

关键词:脆性模量系数;应变软化;渗透率;三轴压缩

责任编辑:许书阁

张春会,赵全胜,王来贵,等.三轴压缩岩石应变软化及渗透率演化的试验和数值模拟[J].煤炭学报,2015,40(8):1774-1782.doi:10.13225/ j.cnki.jccs.2015.0158

岩石三轴试验研究表明,在应力达到峰值强度后,岩石通常发生明显的应变软化现象。随着变形增加,峰后岩石内部裂隙扩展加剧,体积扩容加速,渗透率快速增长,岩石的强度下降并逐渐趋于残余强度。岩石的峰后力学行为与隧道开挖、煤炭和石油等资源开发、地震、岩爆、突透水和瓦斯突出灾害预报及防治等众多岩石工程问题密切相关。因此,研究岩石破坏后的力学特性及行为具有重要工程意义。国内外对大理岩、砂岩、花岗岩、软弱泥岩等开展了大量三轴试验研究[1-10],结果表明围压是影响岩石峰后力学行为的重要因素。围压增加不仅能提高岩石的强度,还能抑制岩石破坏后内部裂隙的扩展和新裂隙萌生,影响岩石峰后的残余强度、脆性、剪胀和渗透性能。Tang 等[11]利用损伤力学方法研究岩石峰后损伤积累及力学性能劣化,开发了相应的数值分析系统RFPA。Fang和Harrison[12-14]提出了强度退化指数的概念,并将其用于模拟围压对岩石峰后残余强度的影响。Yuan和Harrison[15-16]提出了剪胀扩容指数,并通过数值分析研究了剪胀扩容对岩石渗透率的影响。谢和平等[17]提出了煤层增透率模型,并模拟了开采扰动对煤岩体裂隙网络渗透性的影响。Zhao和Cai[18]认为岩石破坏后剪胀不会无限制的发展,据此提出了动态剪胀角的概念。王水林等[19]采用分段塑性方法简化岩石峰后的脆性跌落过程,提出了一种岩石应变软化行为的模拟方法。总体上,上述研究较好地模拟了围压对岩石峰后残余强度和剪胀扩容的影响,但没有考虑围压对岩石峰后脆性的影响。于永江等[20]定义了一个新参数,即退化角来反映围压对岩石峰后脆性的影响,并建立了相应的应变软化模型,模型中假定泊松比恒定。但岩石破坏后的泊松比实际上不是一个常数。

本文对新疆巴里坤砂岩开展三轴压缩和三轴渗流试验。基于试验结果,提出了一个描述围压对岩石峰后脆性影响的新参数,即脆性模量系数,试验数据拟合结果表明,围压与脆性模量系数之间呈负指数关系;基于脆性模量系数,结合强度退化指数和扩容指数建立了一个反映围压对岩石峰后力学行为影响的应变软化模型。分析了巴里坤砂岩体积应变与渗透率的关系,建立了基于体积应变增透率的岩石渗透率演化模型。将建立的岩石峰后应变软化力学模型和渗透率演化模型结合,建立了描述三轴压缩岩石应变软化行为和渗透率演化的力学模型,并在FLAC下予以实现,利用该模型模拟了巴里坤砂岩不同围压下的应变软化行为和三轴压缩条件下的渗透率演化过程。

1 试验结果与分析

1.1 试验概况及试验结果

取新疆巴里坤砂岩样,按国际岩石力学学会标准在实验室加工成ϕ50 mm×100 mm的圆柱试样。

试验在吉林金力电液伺服试验机YAW2000上进行。该试验机主要由主机、轴向伺服油源、三轴压力室和计算机自动测量和控制系统构成试验机围压可达100 MPa,孔隙压60 MPa,最大轴向力2 000 kN,如图1所示。

试验包括三轴压缩试验和三轴渗流试验。

(1)三轴压缩试验。

图1　YAW2000试验系统Fig.1 Test equipment of YAW2000

将砂岩岩样用胶皮套密封,然后置于三轴压力室内,通过围压伺服油源施加围压至预定值,然后轴向位移加载,加载速率为0.002 mm/ s。

(2)三轴渗流试验。

在加工好的试样表面按半桥法贴好应变片,用热缩管密封,然后置于三轴压力室内。通过围压伺服油源加围压至14 MPa。在轴向施加0.4 MPa/ s的力荷载,在荷载施加过程中在试样的上、下两端(入口和出口)施加孔隙气压力(试验气体为N2),入口和出口压力分别为4.5和0.1 MPa,测试流动稳定时的流量,然后使用达西定律计算渗透率。

按照上述试验步骤开展试验,得到不同围压下巴里坤砂岩的全程应力应变曲线如图2所示。14 MPa围压下砂岩的渗透率、体积应变和时间关系曲线如图3所示。

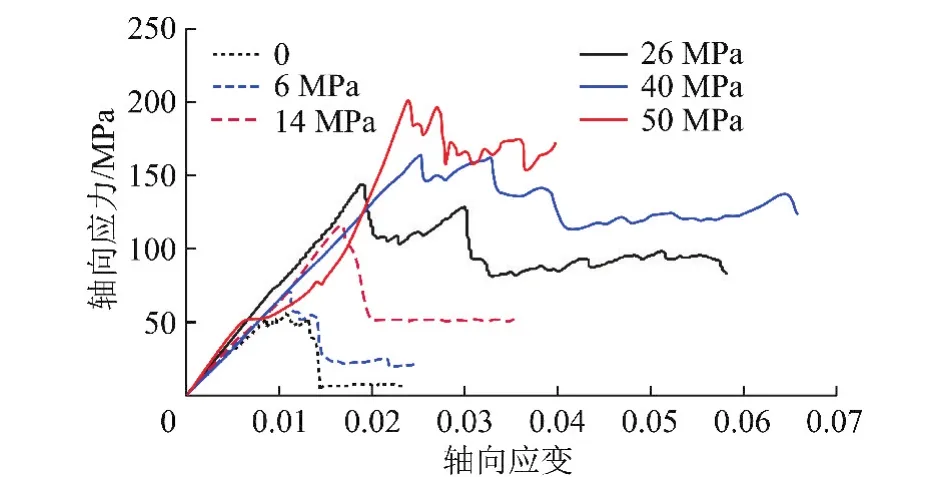
图2　砂岩三轴试验全程应力应变曲线Fig.2 Whole stress-strain curves of sandstoneunder tri-axial compression

1.2 试验结果分析

由图2可见,围压对岩石峰后应变软化行为有很大影响。随着围压增加,岩石的残余强度增加,岩石峰后的脆性则随着围压增加而减小。

由图3可见,岩样渗透率和体积应变密切关联,两者都随着时间增加而呈先减小后增加的“V”型变化。在图3中,根据岩样渗透率的变化及趋势,可以将渗透率渗透率和体积应变曲线划分为3个阶段。AB段是第1阶段,这一阶段岩样发生弹性压缩,岩样内部裂隙闭合,岩样的渗透率降低。BC段是第2阶段,这一阶段是一个过渡阶段,B点近似为岩石的屈服强度,C点在岩样的峰值强度附近,这一阶段的范围近似从岩样屈服开始,至岩样破坏前终止。在这一阶段,岩样内的微裂隙开始扩展,岩样体积应变变化幅度不大,相应的渗透率基本保持不变或略有增长。CD段是第3阶段,开始于岩样峰值强度附近。在这一阶段,岩样内裂隙快速扩展、新裂隙萌生,岩样的体积应变快速增长,相应的渗透率也显著增长。

渗透率是空隙空间的函数,空隙空间越大,渗透率越大。由于岩石固体颗粒通常不易发生胀缩,三轴条件下岩石的胀缩主要是空隙空间的胀缩。体积应变反映了岩石空隙空间的变化。因此,可使用体积应变来描述岩石的渗透率演化。本文仅开展了14 MPa围压下的三轴渗流试验,在其他围压下渗透率与体积应变之间也符合上述规律,这已为大量的三轴渗流试验结果[3,9,21-22]所证实。

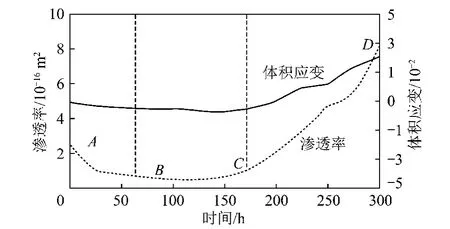
图3　砂岩的渗透率-体积应变与时间的关系Fig.3 Permeability and volumetric strain with the time for sandstone

2 基于体积应变增透率的渗透率演化模型

定义体积应变增透率为单位体积应变变化引起的渗透率改变,其数学形式可写为

式中,η为渗透率;εV为体积应变。

则渗透率可以表示为

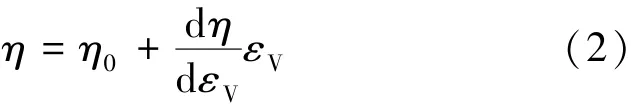
式中,η0为无体积应变时的渗透率。

体积应变增透率λ由三轴渗流试验获得的渗透率与体积应变试验数据对通过数据拟合确定,一般为如下形式:

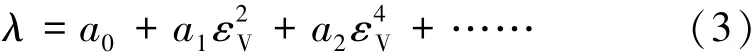
式中,a0,a1,a2,……为拟合常数。

在实际应用中取式(3)中的前2项或前1项就可取得较好拟合效果。

式(3)中体积应变之所以取偶数指数形式,主要是将式(3)代入式(2)中后,右边的增量是关于体积应变的奇次方项,这可以较好考虑应变正负号的影响。

由图3绘制14 MPa围压下砂岩的渗透率与体积应变关系曲线如图4所示。

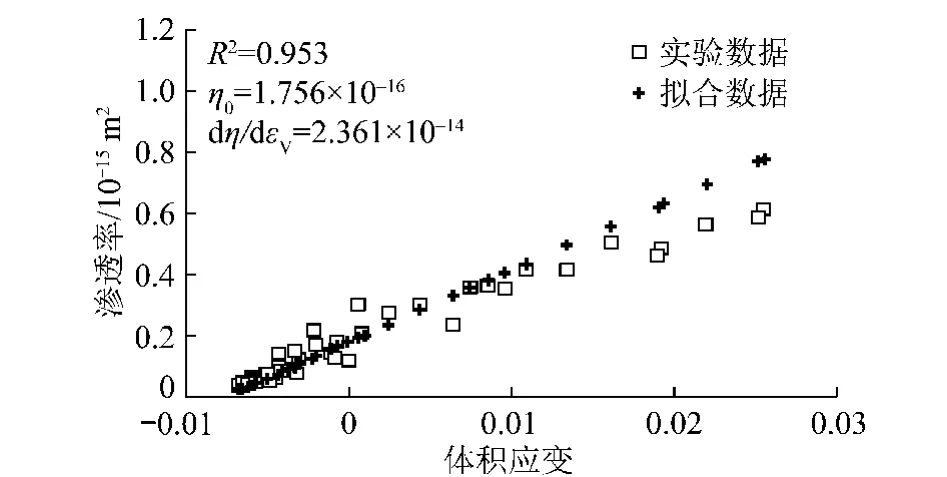
图4　砂岩的渗透率与体积应变Fig.4 Permeability and volumetric strain for sandstone

由图4可见,渗透率与体积应变之间服从直线关系,体积应变增透率λ为常数,渗透率可以表示为

η= 1.756×10-16+ 2.361×10-14εV(4)

3 岩石应变软化模型

由式(4)可见,准确计算三轴压缩下岩石的体积应变是预测岩石渗透率演化的基础。

巴里坤砂岩和其他岩石三轴试验数据[1-2,4,6-7,10]表明,岩石通常是一种应变软化材料,围压对岩石峰后应变软化行为有很大影响,如图5所示,具体体现为:

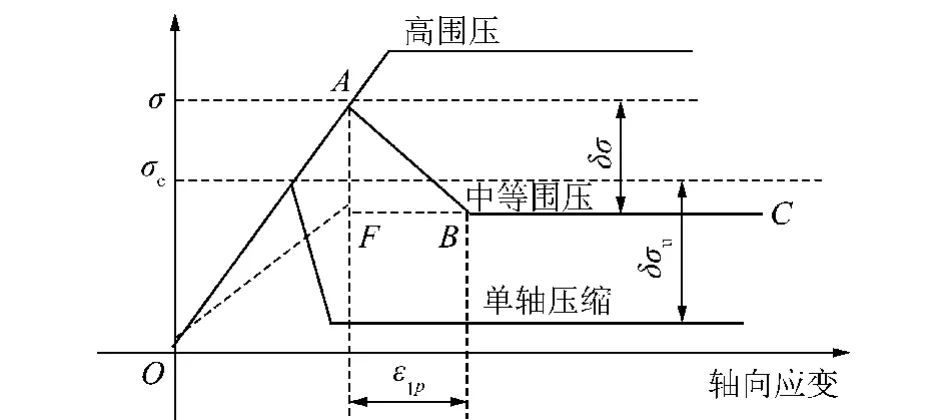
图5　简化的岩石三轴应力应变曲线Fig.5 Simplified stress-strain curves under tri-axial compression

(1)以图5所示的tan∠ABF来描述围压对岩石峰后强度退化过程的影响,则随着围压增加,tan∠ABF减小,即随着围压增加,岩石峰后强度退化的脆性减小,塑性增加。

(2)随着围压增加,岩石的残余强度增加,岩石的强度降减小。

(3)随着围压增加,岩石峰后裂隙扩展减弱,岩石的体积扩容速率减小,如图6所示。

下面使用脆性模量系数、强度退化指数和扩容指数来描述三轴压缩岩石的上述特征,建立相应的岩石应变软化模型。

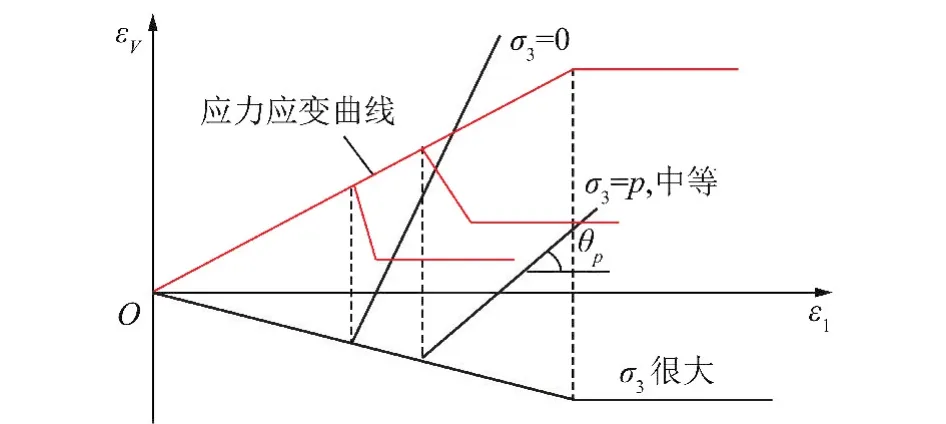
图6　三轴压缩下岩石的体积扩容特征Fig.6 Volumetric dilatation properties under tri-axial compression

3.1 脆性模量系数

将图5中的∠ABF定义为脆性模量,表示为

式中,δσ为三轴压缩岩样峰后强度退化值;ε1p为三轴压缩岩样由峰值强度降至残余强度的轴向塑性应变,如图5所示。

由图1和图5可见,围压对脆性模量有很大影响,围压增加,岩石峰后脆性减弱,塑性增强,脆性模量在单轴条件下最大。定义脆性模量系数η为

式中,Eb0为岩样单轴下的脆性模量。

由式(6)可知,脆性模量系数介于0~1之间。单轴压缩时其值为1,随着围压增加而减小,在高围压时其值接近为0。

由巴里坤砂岩[10],Tennessee大理岩[12]和山西含碳泥岩[7]三轴试验数据得到的脆性模量和脆性模量系数见表1。

将脆性模量系数和围压数据绘于图7中,可以看出脆性模量系数η与围压之间近似服从负指数函数关系,即

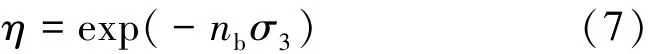
式中,nb为常数,由试验数据拟合确定;σ3为围压。

用式(7)拟合表中脆性模量系数与围压的试验数据,结果如图7所示。由图7可见,式(7)能很好地拟合围压对脆性模量系数的影响。

3.2 破坏准则

使用Mohr-Column准则判断岩石单元是否发生破坏,Mohr-Column准则为

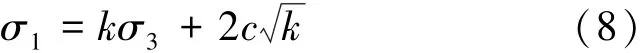
式中,k=(1+sin φ) / (1-sin φ);φ为内摩擦角;c为黏聚力;σ3为小主应力;σ1为大主应力。

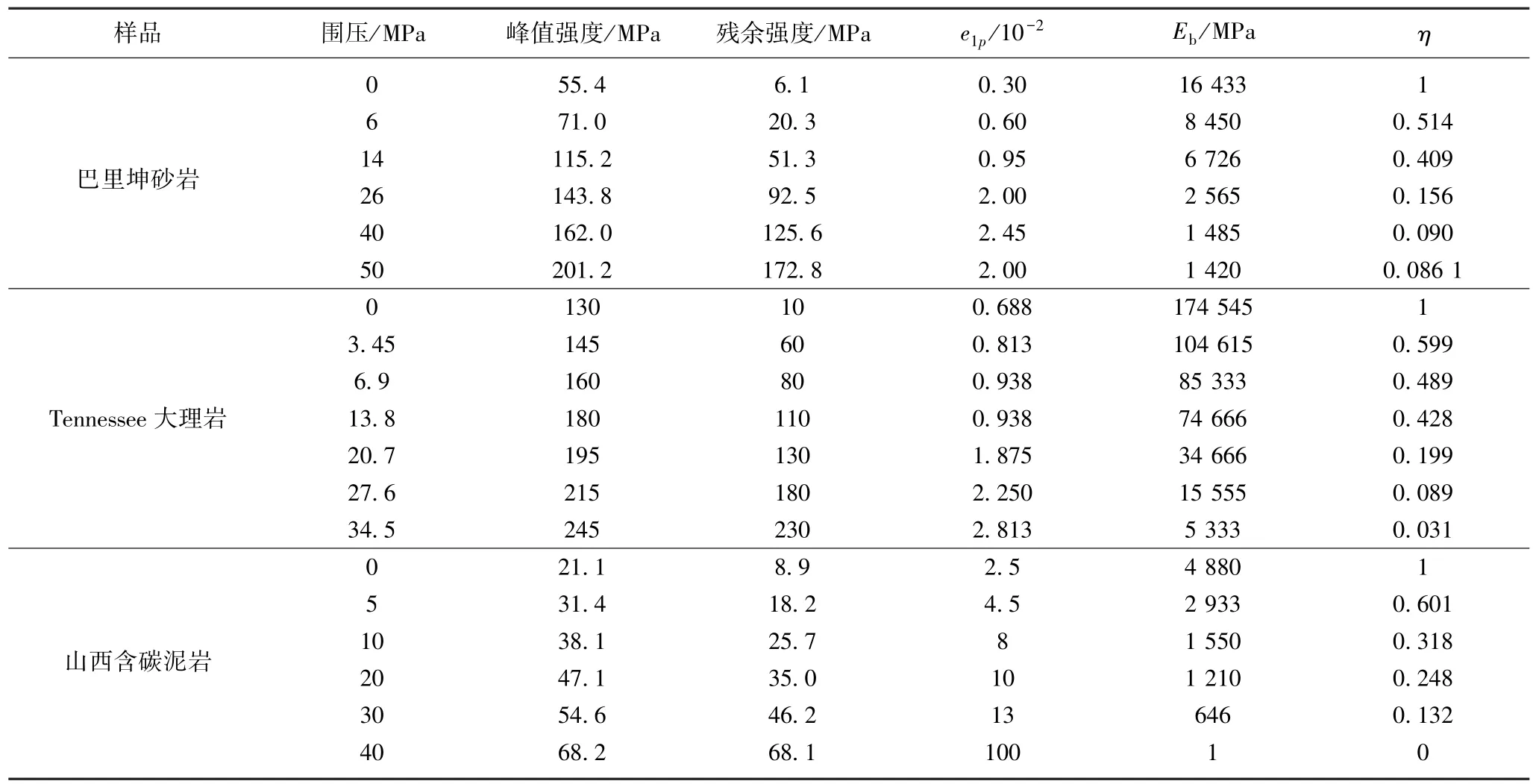
表1　脆性模量系数[7,10,12]Table 1 Brittle modulus index[7,10,12]

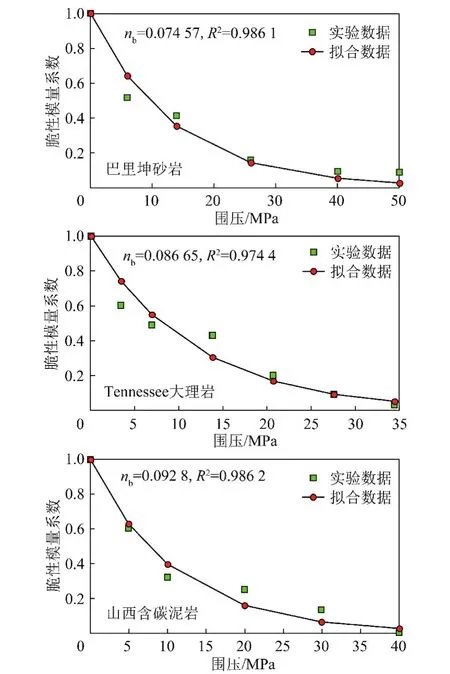
图7　围压对脆性模量系数的影响Fig.7 Effects of confinement on brittle modulus index

3.3 残余强度

以往研究结果表明[12-14],考虑围压影响的岩石残余强度可以表示为

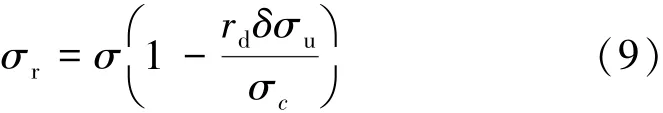
式中,σr为残余强度对应的大主应力;δσu为单轴条件下岩石峰后的强度降;σ为σ3围压下岩石的峰值强度;rd为FANG建议的强度退化指数,其值与围压的关系[12]可表示为

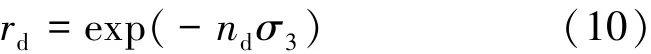
式中,nd为常数,由试验数据拟合确定[12]。

岩石峰后残余强度屈服面仍假设为Mohr-Column屈服面,并可表示为

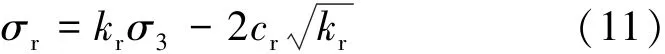
式中,cr为相应的残余黏聚力;kr= (1+sin φr) / (1-sin φr);φr为残余内摩擦角。

岩石峰后残余强度屈服面所对应的残余内摩擦角和黏聚力通过如下步骤确定:

(1)由式(9)和(10)计算不同围压下岩石的残余强度,获得围压与残余强度数据对;

(2)然后利用式(11)结合非线性拟合方法确定残余内摩擦角和残余黏聚力。

3.4 剪胀扩容

岩石的剪胀扩容是由于岩石内部微裂隙扩展或滑动块体错动抬升造成的。若岩石施加围压,则裂隙的扩展或滑动块体的抬升都会受到影响。试验结果已经表明,围压对岩石的剪胀扩容有很大影响,随着围压增加,岩石的剪胀扩容速率趋缓,当围压足够大时,岩石的剪胀扩容基本消失,如图6所示。

为了描述围压对岩石剪胀扩容的影响[15-16], Yuan等定义了扩容指数:

式中,ΔεVp和Δε1p分别为塑性体积应变和塑性轴向应变;下标“0”和“p”分别表示单轴和围压为p的情况;θp轴向塑性应变与体积塑性应变直线的夹角,如图6所示。

于是

θ0使用剪胀角表示为

式中,ψ0为单轴下剪胀角。

Id与围压之间服从如下经验关系[15]:

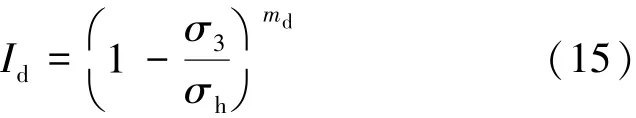
式中,σh为无剪胀时的围压值;md为拟合常数,由三轴试验通过数据拟合确定[15]。

而

由式(13)~(16)可以得到p围压下的剪胀角为

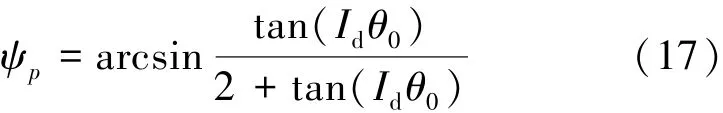
3.5 等效塑性应变

本文利用FLAC[23]中的SS模型实现本文的岩石应变软化模型。其中通过式(17)结合岩石单元的应力水平确定相应的剪胀角。

岩石的应变软化是通过岩石内摩擦角和黏聚力退化来定义。这通过FLAC中的表(table)来实现,如图8所示。图8中,εps为从峰值强度降至残余强度过程中的等效塑性应变;φ0和c0为岩石内摩擦角和黏聚力;φr和cr为残余内摩擦角和残余黏聚力,由3.3节中的式(9)~(11)确定。

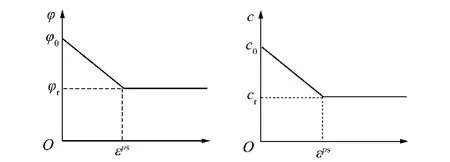
图8　内摩擦角和黏聚力退化Fig.8 Degradation of internal friction angle and cohesion

为了便于应用,使用轴向塑性应变来表示等效塑性应变,具体过程如下。

FLAC中的等效塑性应变[23]可以表示为

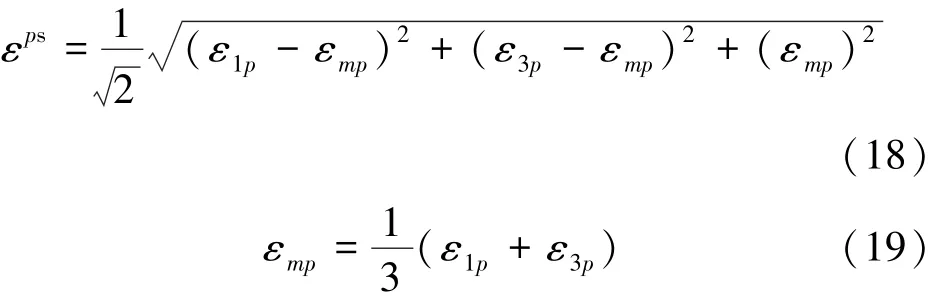
式中,ε1p,ε3p分别为轴向和径向塑性主应变分量。

非相关联流动法则[23]可表示为

式中,Nψ=(1+sin ψp) / (1-sin ψp);ψp为σ3围压时的剪胀角,利用式(17)计算。

塑性主应变分量[23]可表示为

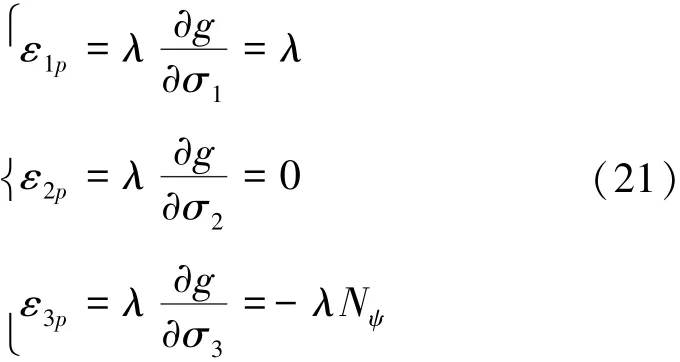
式中,λ为塑性因子。

由式(21),(18)和(19),有[23]:

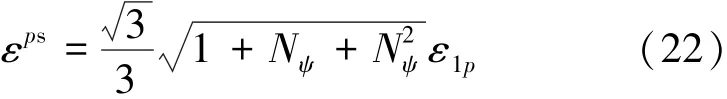
式中,ε1p为从峰值强度降至残余强度过程中的轴向塑性应变。

通过式(6)和(7),ε1p为

等效塑性应变表示为

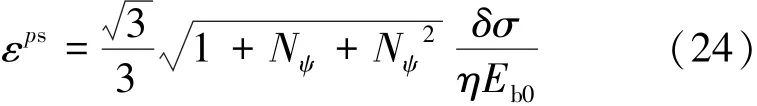
4 数值实现

本文利用FLAC中的SS模型和Fish函数方法模拟岩石峰后的应变软化行为和渗透率的演化。

数值实现的基本过程为:

(1)划分计算网格,材料模型定义,定义初边值条件。

(2)定义材料参数。其中残余内摩擦角和残余黏聚力由强度退化指数确定。剪胀角由应力水平通过扩容指数确定。等效塑性应变由应力水平通过脆性模量系数确定。

(3)由体积应变,利用式(4)计算渗透率。

(4)计算开始,每20时步重新计算强度退化指数、扩容指数和脆性模量系数,计算相关参数,重新进行参数赋值。

5 数值模拟

5.1 巴里坤砂岩变形及渗透率演化

在FLAC下建立巴里坤砂岩的三轴压缩数值模型。数值模型中的岩石物理力学参数见表2[10]。

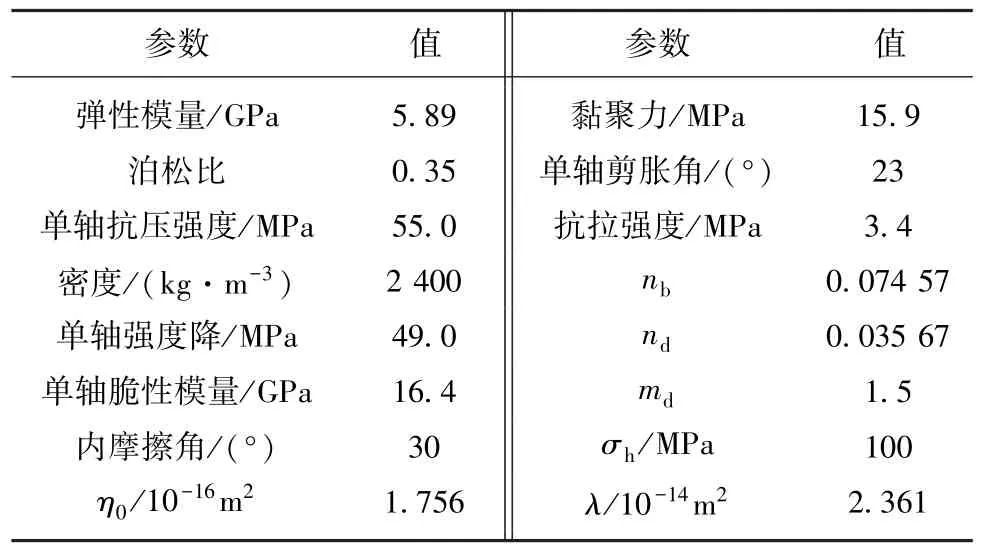
表2　巴里坤砂岩的物理力学参数Table 2 Physical and mechanical parameters forBalikun sandstone

圆柱形数值模型的尺寸为ϕ50 mm×100 mm (高度),在试样侧面施加围压,其值分别为0,6,14,26,40 和50 MPa。轴向施加位移,速度为1.5×10-8m/ step。

图9为数值岩样和试验岩样不同围压下全程应力应变曲线的对比。由图9可见,数值模拟结果与试验结果基本一致,这表明本文模型可以较好地考虑围压对岩石残余强度和峰后脆性的影响,本文模型是合理的。

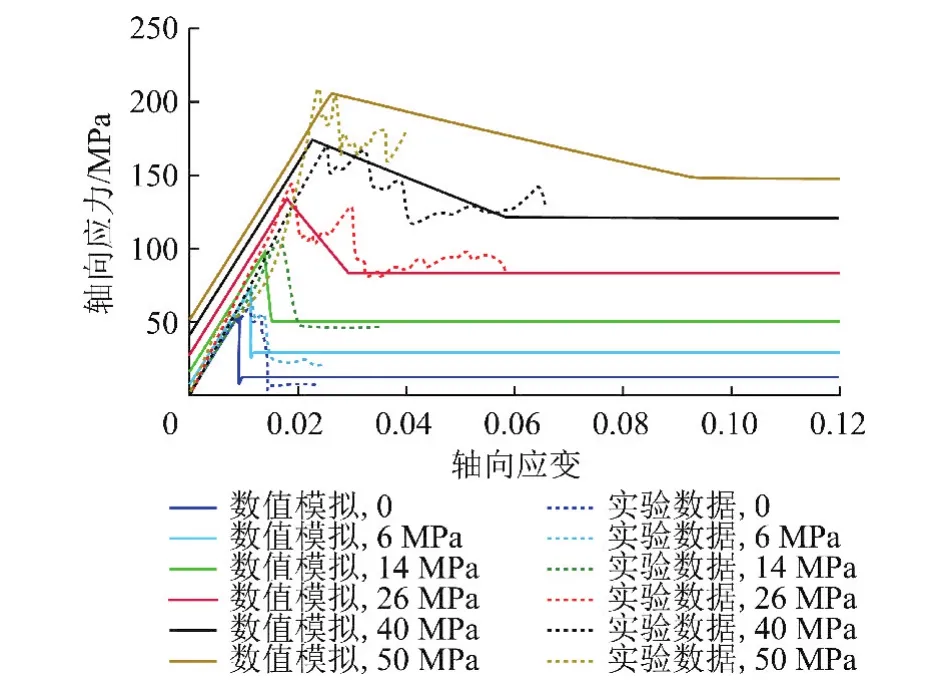
图9　三轴压缩岩样的全程应力应变曲线Fig.9 Axial stress and axial strain curves undertri-axial compression

图10为数值模拟得到的不同围压下渗透率与轴向应变的关系曲线和14 MPa下渗透率与轴向应变关系的实测曲线。从数值模拟结果可见,在开始阶段,岩样发生弹性压缩,渗透率降低;在岩样破坏后,由于岩样内的裂隙扩展和新裂隙萌生,岩样体应变增加,体积扩容,渗透率增长。总体上,数值岩样的渗透率呈“V”型变化,这与试验结果一致。

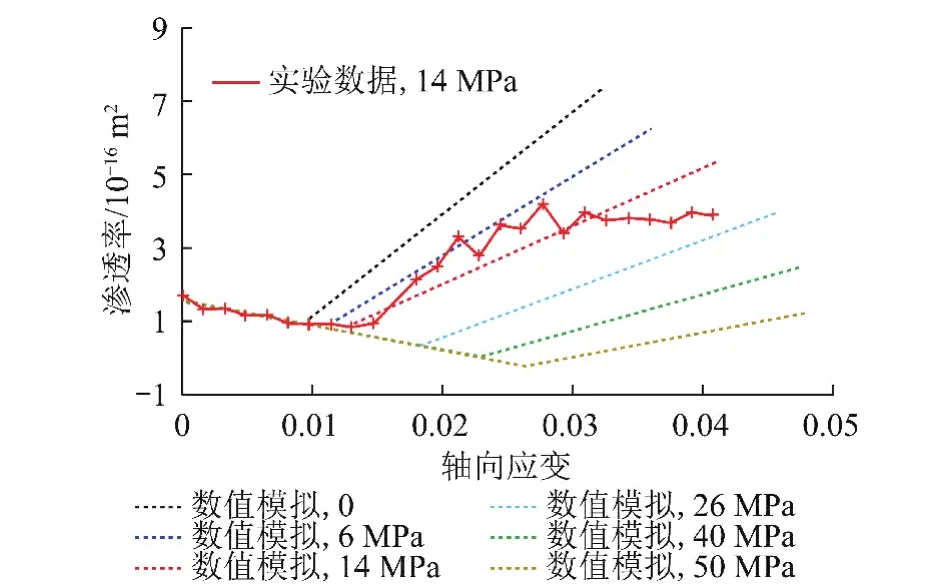
图10　不同围压下轴向应变与渗透率的关系曲线Fig.10 Permeability and axial strain curves obtained from tests and numerical simulation under varied confining pressure

由图10可见,围压能限制岩样的剪胀扩容,随着围压增加,岩样的渗透率增长速率趋缓。对比14 MPa下岩样渗透率试验结果和数值计算结果,可以发现数值结果与试验结果基本一致,可见本文模型能较好地模拟岩石变形破坏过程中的渗透率演化。

由图10中岩样的渗透率试验数据还可以发现,岩样的渗透率先减小,而后有一缓慢增加的过渡段,该阶段始于峰前,应力值约为峰值强度的2/3,大致终止于峰值强度。这表明加载过程中当应力达到岩样峰值强度的2/3时,内部裂隙开始扩展,但扩展速率缓慢,这时岩样的渗透率开始缓慢增长。以往研究[21-22]一般假设岩石破坏,剪胀扩容开始,渗透率增长。本文也采用了这一假设。从试验数据来看,由于过渡段岩石的渗透率变化不大,因此这一假设基本是合理的。

由图11中岩样的渗透率试验结果可见,岩样破坏后渗透率继续增长,但当渗透率增长到一定程度,增长速率快速趋缓,甚至不再增长。之所以如此,主要是岩石破坏后裂隙扩展、逐渐贯通。在这之后再增加荷载,裂隙基本不再扩展,渗透率也不再明显增加。本文模型还不能很好地反映岩样渗透率变化的这一特征。

5.2 岩样渐进破坏过程中的渗透率演化

岩样渐进破坏过程中的渗透率演化是采动岩石渗透率演化及相关灾害预测预报研究的基础。这里利用本文模型分析岩样渐进破坏过程中的渗透率演化。

为了便于观察,分析中采用平面应变模型。模型尺寸为50 mm(宽)×100 mm(高),侧向的围压分别取10和20 MPa,竖向位移加载,加载速度为2.0× 10-8m/ step。

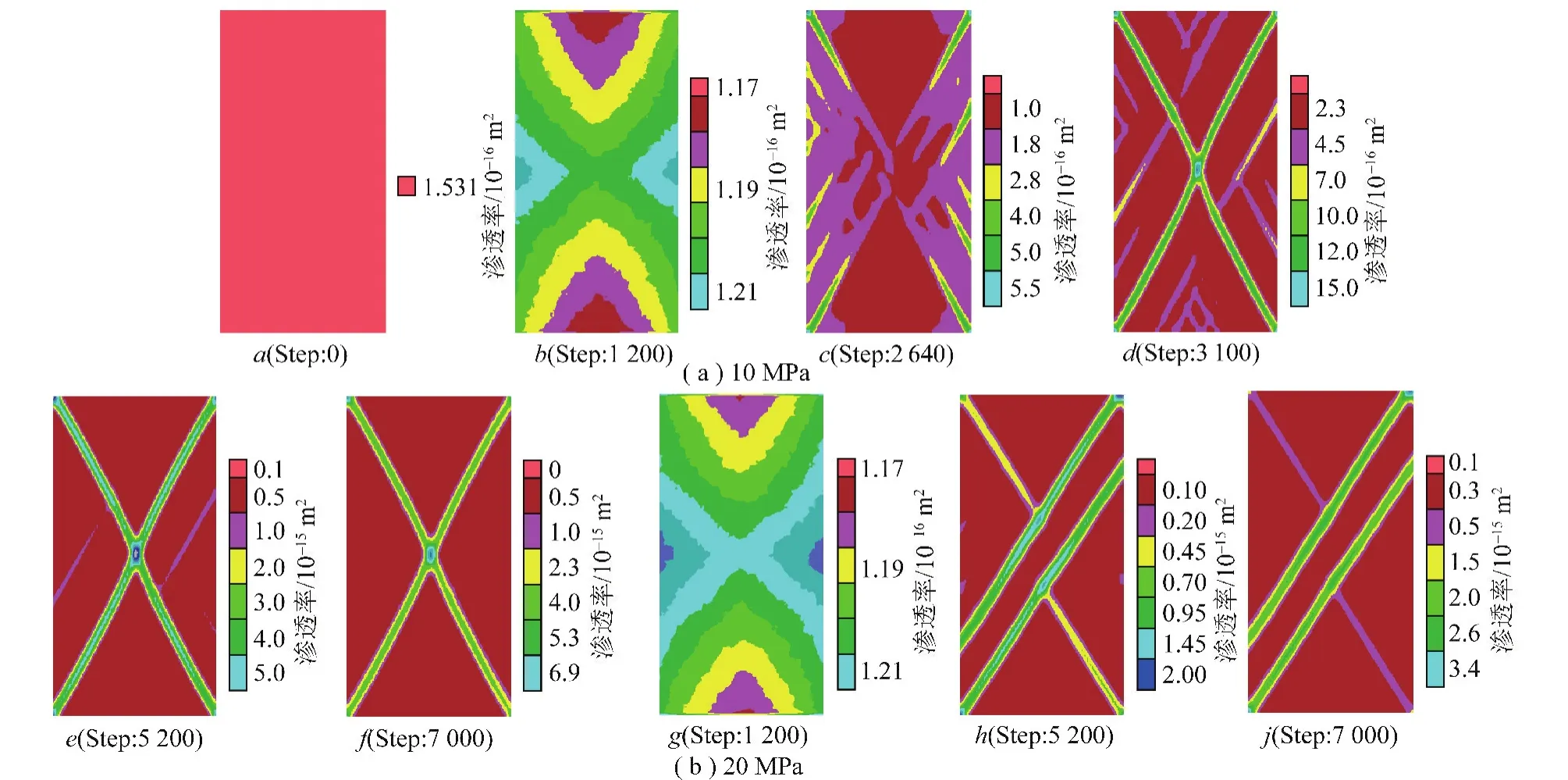
图11　数值岩样的渗透率演化Fig.11 Evolution of permeability in the numerical sample

图12为10和20 MPa侧压下数值岩样的轴向应力、体积应变和轴向应变关系曲线。由图12能明显观察到岩石峰后应变软化和剪胀扩容行为。同时还可以发现,随着围压增加,岩石的峰值强度和残余强度都增长,剪胀扩容速率趋缓,峰后脆性减弱,塑性增强。

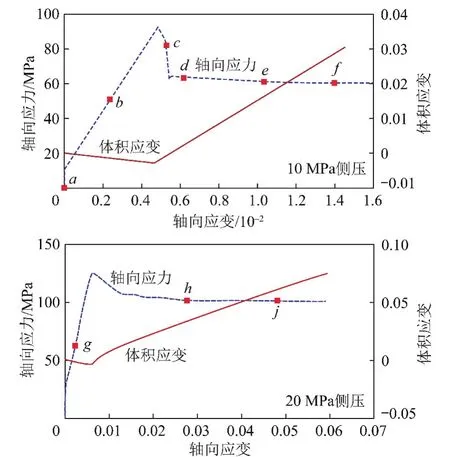
图12　岩样的轴向应力、体积应变与轴向应变关系Fig.12 Modeling stress,volumetric strain with axial strain with the confining pressure

图11给出了10和20 MPa侧压下不同加载阶段(图12中a~j点)数值岩样的渗透率演化图。由图11可见,在线弹性阶段弹性压缩使得岩样内的孔隙和裂隙闭合,岩样的渗透率降低。围压增加使得岩样孔隙和裂隙空间压缩加剧,岩样的渗透率减小。

当应力达到峰值强度后,由于剪胀扩容,岩样的渗透率急剧增长,相比于初始渗透率,增加了1~2个数量级。围压对岩样峰后的渗透率演化也有很大影响。围压能抑制岩样峰后剪胀发展,从而也将抑制岩样峰后渗透率的增长。

由图11还可以发现,岩样在峰值强度后出现了明显的剪切破坏带,剪切破坏带与大主应力的夹角随着围压的增加而增大。在剪切破坏带内单元的渗透率显著增长,最后形成了一个流动通道。

6 结 论

(1)围压对岩石峰后应变软化行为有很大影响。随着围压增加,岩石峰后残余强度增加,体积扩容和脆性减弱。脆性模量系数可以较好地描述围压对岩石峰后脆性的影响,围压与脆性模量系数之间服从负指数关系。

(2)岩石应变软化模型能很好地模拟围压对岩石残余强度、体积扩容和峰后脆性的影响。

(3)随着轴向应变增加,岩石先发生弹性压缩,空隙空间减小,渗透率降低;当应力达到屈服强度,岩石内裂隙开始扩展,渗透率降低速率趋缓;在峰值应力后,岩样破坏,裂隙扩展加速,并伴有新裂隙的萌生,岩样渗透率开始快速增长,岩样的渗透率呈“V”型变化。另外,围压对岩样的渗透率也有很大影响,随着围压增加,岩样的渗透率增长速率趋缓。

(4)本文模型能较好地模拟围压和剪胀扩容对岩石渗透率的影响。

(5)峰后岩样内出现了明显的剪切破坏带,剪切破坏带与大主应力的夹角随着围压的增加而增大。在剪切破坏带内单元的渗透率显著增长,最后形成了一个流动通道。

参考文献:

[1]Bésuelle P,Desrues J,Raynaud S.Experimental characterization of the localisation phenomenon inside a Vosges sandstone in a triaxial cell[J].Int.J.Rock Mech.Min.Sci.,2000,37:1223-1237.

[2]Rakesh Kumar,Sharma K G,Varadarajan A.Post-peak response of some metamorphic rocks of India under high confining pressures [J].Int.J.Rock Mech.Min.Sci.,2010,47:1357-1362.

[3]Badrul AlamA K M,Masaki Niioka,Yoshiaki Fujii,et al.Effects of confining pressure on the permeability of three rock types under compression [J].International Journal of Rock Mechanics & Mining Sciences,2014,65:49-61.

[4]张春会,徐晓攀,王锡朝,等.考虑围压影响的岩石弹脆塑力学模型[J].采矿与安全工程学报,2015,32(1):132-137.

Zhang Chunhui, Xu Xiaopan, Wang Xizhao, et al.Elastic-brittleplastic mechanical model for rock with confining pressure[J].Journal of Mining & Safety Engineering,2015,32(1):132-137.

[5]许 江,李波波,周 婷,等.加卸载条件下煤岩变形特性与渗透特征的试验研究[J].煤炭学报,2012,37(9):1493-1498.

Xu Jiang,Li Bobo,Zhou Ting,et al.Experimental study of coal deformation and permeability characteristics under loading-unloading conditions[J].Journal of China Coal Society,2012,37(9): 1493-1498.

[6]张 帆,盛 谦,朱泽奇,等.三峡花岗岩峰后力学特性及应变软化模型研究[J].岩石力学与工程学报,2008,27(S1):2651-2655.

Zhang Fan,Sheng Qian,Zhu Zeqi,et al.Study of post-peak mechanical behavior and strain-softening model of Three Gorges granite[J].Chinese Journal of Rock Mechanics and Engineering, 2008, 27 (S1):2651-2655.

[7]陆银龙,王连国,杨 峰,等.软弱煤岩峰后应变软化力学特性研究[J].岩石力学与工程学报,2010,29(3):640-648.

Lu Yinlong,Wang Lianguo,Yang Feng,et al.Post-peak strain softening mechanical properties of weak rock[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):640-648.

[8]彭守建,许 江,尹光志,等.煤岩破断与瓦斯运移耦合作用机理的试验研究[J].煤炭学报,2011,36(12):2024-2028.

Peng Shoujian,Xu Jiang,Yin Guangzhi,et al.Experimental study on the coupling mechanism between coal fracture and gas migration [J].Journal of China Coal Society,2011,36(12):2024-2028.

[9]于永江,张 华,张春会,等.温度及应力对成型煤样渗透性的影响[J].煤炭学报,2013,38(6):936-941.

Yu Yongjiang,Zhang Hua,Zhang Chunhui,et al.Effects of temperature and stress on permeability of standard coal briquette specimen [J].Journal of China Coal Society,2013,38(6):936-941.

[10]张春会,赵全胜.饱水度对砂岩强度和模量影响的三轴试验[J].岩土力学,2014,35(4):951-958.

Zhang Chunhui,Zhao Quansheng.Triaxial tests of effects of varied saturations on strength and modulus for sandstone [J].Rock and Soil Mechanics,2014,35(4):951-958.

[11]Tang C A,Liu H,Lee P K K,et al.Numerical studies of the influence of microstructure on rock failure in uniaxial compression-Part I:Effect of heterogeneity[J].Int.J.Rock Mech.Min.Sci.,2000, 37:555-569.

[12]Fang Z,Harrison J P.A mechanical degradation index for rock[J].Int.J.Rock Mech.Min.Sci.,2001,38:1193-1199.

[13]Fang Z,Harrison J P.Development of a local degradation approach to the modelling of brittle fracture in heterogeneous rocks[J].Int.J.Rock Mech.Min.Sci.,2002,39:443-457.

[14]Fang Z,Harrison J P.Application of a local degradation model to the analysis of brittle fracture of laboratory scale rock specimens under triaxial conditions[J].Int.J.Rock Mech.Min.Sci.,2002,39: 459-476.

[15]Yuan S C,Harrison J P.An empirical dilatancy index for the dilatant deformation of rock[J].Int.J.Rock Mech.Min.Sci.,2004, 41:679-686.

[16]Yuan S C,Harrison J P.Development of a hydro-mechanical local degradation approach and its application to modelling fluid flow during progressive fracturing of heterogeneous rocks [J].Int.J.Rock Mech.Min.Sci.,2005,42:961-984.

[17]谢和平,高 峰,周宏伟,等.煤与瓦斯共采中煤层增透率理论与模型研究[J].煤炭学报,2013,38(7):1101-1108.

Xie Heping, Gao Feng, Zhou Hongwei, et al.On theoretical and modeling approach to mining-enhanced permeability for simultaneous exploitation of coal and gas[J].Journal of China Coal Society,2013,38(7):1101-1108.

[18]Zhao X G,Cai M.A mobilized dilation angle model for rocks[J].Int.J.Rock Mech.Min.Sci.,2010,47:368-384.

[19]王水林,郑 宏,刘泉声,等.应变软化岩体分析原理及其应用[J].岩土力学,2014,35(3):609-613.

Wang Shuilin,Zheng Hong,Liu Quansheng,et al.Principle of analysis of strain-softening rock mass and its application [J].Rock and Soil Mechanics,2014,35(3):609-613.

[20]于永江,张春会,王来贵.基于退化角的岩石峰后应变软化模型[J].煤炭学报,2012,37(3):402-406.

Yu Yongjiang,Zhang Chunhui,Wang Laigui.Post-peak strain softening model of rock based on degradation angle[J].Journal of China Coal Society,2012,37(3):402-406.

[21]Xin Tan,Heinz Konietzky,Thomas Frühwirt.Laboratory observation and numerical simulation of permeability evolution during progressive failure of brittle rocks[J].Int.J.Rock Mech.Min.Sci.,2014, 68:167-176.

[22]于永江,张春会,赵全胜,等.承载围岩渗透率演化模型及数值分析[J].煤炭学报,2014,39(5):841-848.

Yu Yongjiang,Zhang Chunhui,Zhao Quansheng,et al.Permeability model for loaded rock and numerical analysis[J].Journal of China Coal Society,2014,39(5):841-848.

[23]ITASCA.Fast lagrangian analysis of continua,Version 5.0[M].Minnesota,2012.

Zhang Chunhui,Zhao Quansheng,Wang Laigui,et al.Test and numerical modeling on strain softening behavior and permeability evolution of rock under tri-axial compression[J].Journal of China Coal Society,2015,40(8):1774-1782.doi:10.13225/ j.cnki.jccs.2015.0158

Test and numerical modeling on strain softening behavior and permeability evolution of rock under tri-axial compression

ZHANG Chun-hui1,2,ZHAO Quan-sheng1,WANG Lai-gui2,ZHAO Na2,YU Yong-jiang2

(1.School of Civil Engineering,Hebei University of Science and Technology,Shijiazhuang 050018,China;2.Department of Mechanics and Science Engineering,Liaoning Technical University,Fuxin 123000,China)

Abstract:The strain softening behaviors and permeability evolution laws of post-peak rock are the basis of the stability analysis of rock engineering.The tri-axial compression tests and tri-axial compression-seepage tests for the sandstone samples from Balikun Mine,Xinjiang were carried out in this paper.The whole stress-strain curves under varied confinement and the curve of volumetric strain and permeability were obtained.The test results show that:with the increase of confining pressure,the dilatancy and brittleness of rock decreases and the residual strength increases.With

the increase of axial strain,the rock takes firstly on elastic compression,and the void space reduces,then the permeability decreases.The fractures in rock begin to expand when the stress reaches yield strength stress.As a result,the reduction rate of permeability slows down.After peak stress,the rock samples fail,and the fractures expand quickly and the new cracks form.Then the permeability begins to increase rapidly,and the permeability takes on“V”type.A new parameter,namely brittle modulus index,which is used to describe the effects of confinement on brittleness after peakpost rock,is presented.The relationship between confining pressure and brittle modulus index takes on a negative exponential form.Based on brittle modulus index,the strength degradation index and dilatancy index,a new strain softening model is established.The relationship between volumetric strain and permeability is investigated,and a permeability evolution model is established based on the enhanced permeability of volumetric strain.In FLAC the strain softening behavior and permeability evolution of Balikun sandstone under tri-axial compression are numerically modeled.The results show that the model in this paper can better describe the effects of confining pressure on the post-peak rock’s brittleness,dilation and residual strength.The model in this paper can better describe the effects of confining pressure and dilatancy on the permeability evolution of rock.A distinct band of degraded and dilated elements forms in the postpeak region,and the angle between these bands and the major principal stress increases as confining pressure increases.Lastly the band of highly permeable elements becomes a flow channel.

Key words:brittle modulus index;strain softening;permeability;tri-axial compression

作者简介:张春会(1976—),男,辽宁沈阳人,教授。Tel:0311-81668904,E-mail:zhangchunhui789@126.com

基金项目:国家自然科学基金资助项目(51274079,51274110,51574139)

收稿日期:2015-02-02

中图分类号:TD315

文献标志码:A

文章编号:0253-9993(2015)08-1774-09