锚索设计参数对复杂地基导流墙预应力锚固的影响分析

毕晨曦，李守义

(西安理工大学 水利水电学院， 陕西 西安 710048)

锚索设计参数对复杂地基导流墙预应力锚固的影响分析

毕晨曦，李守义

(西安理工大学 水利水电学院， 陕西 西安 710048)

预应力锚索加固是一种比较成熟的岩土加固技术，已广泛应用于许多工程，同时预应力锚固是改善结构稳定性的重要手段。基于ANSYS有限元软件进行模拟计算,利用预应力锚索加固复杂地基导流墙，研究了锚索设计参数对复杂地基导流墙预应力锚固的影响，提出针对台阶状复杂地基的布锚方式。结果表明：锚索设计参数对复杂地基导流墙预应力锚固有不同程度的影响，导流墙的侧向抗滑稳定对锚固角、锚固高程及锚固间距的变化极其敏感，锚固效果受锚固高程的影响最为显著。

预应力锚索；锚索设计参数；导流墙；降温值

在水利工程中，导流墙作为一种导流建筑物极为常见，其基础的抗滑稳定至关重要。预应力锚索作为一种岩土加固技术，从20世纪50年代后期起，在我国开始使用锚杆支护，1964年在梅山水库连拱坝左、右坝肩加固中，首次使用了预应力锚索[1]。根据可查阅的相关资料，1987年铜街子工程中为了防止导墙基础深层滑动，对比钢筋拉锚、预应力锚固及单锚桩三种加固方案，最终确定采用预应力锚束加固墙基；2012年桥巩水电站由于地基存在软弱结构面，二期导流时同样是为了满足深层抗滑稳定，采用了预应力锚索加固纵向导墙[2]，此外，该水电站在处理闸室左边坡的深层滑裂面时，依旧采用了预应力锚索进行加固[3]。

近年来，针对预应力锚索加固技术的研究已有很多研究成果，如陈祖煜，张发明等[1，4]应用优化与决策理论，提出了确定岩锚设计参数的优化方法；李宁等[5]对于岩质边坡预应力锚固的设计原则与方法做了详细的探讨，提出了诸多关于锚索设计时所需考虑的因素以及计算公式；林兴超等[6]针对边坡与边坡加固措施之间的相互作用很难通过数值计算确定，提出了一种简单的数值模拟技术；邓宗伟等[7]在研究预应力锚索荷载传递与锚固效应的过程中，提出锚索设计参数中，相邻锚索之间的最小距离应以正应力为标准进行控制；詹筱霞等[8]针对贵州沙陀水电站预应力锚索在坝基抗滑稳定中的应用，详细阐述了锚索的设计方法、布置方案施工技术等。然而这些结论在导流墙加固时是否同样适用，导流墙加固时锚索设计参数应怎样考虑，特别是针对折线台阶状地基，锚索设计参数的选择以及布锚的形式仍有待研究分析。

本文结合工程实例，采用ANSYS有限元软件进行模拟计算，拟采用不同的加固方案，通过对导流墙侧向抗滑稳定的计算，对比总抗力与总作用效应的差值Δ(此差值Δ定义为抗滑稳定安全富裕度)，来研究分析锚索设计参数对导流墙侧向抗滑稳定的影响，为复杂地基上的导流墙加固提供依据。

1 复杂地基导流墙结构形式

某水电站由于受地形和地质条件的限制，施工期导流明渠的建基面高程1 761.0 m，与其相邻的右侧电站厂房建基面高程1 737.0 m，导流明渠建基面高程远高于厂房建基面高程，导流明渠的右侧导墙高60 m，建基面为左侧高右侧低的台阶状，折线台阶状复杂地基对导流墙的侧向稳定极为不利，故必须对导流墙进行预应力锚索加固，如图1、图2所示。

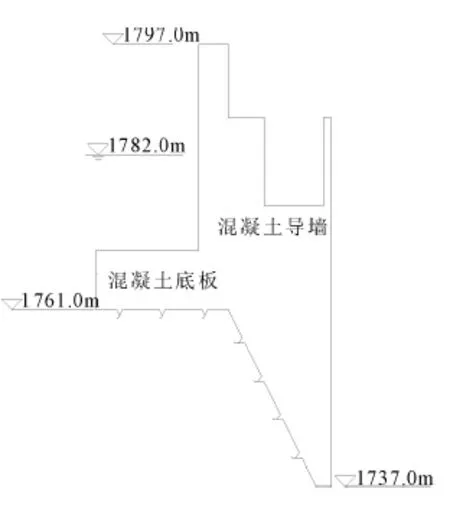
图1 导流墙结构示意图

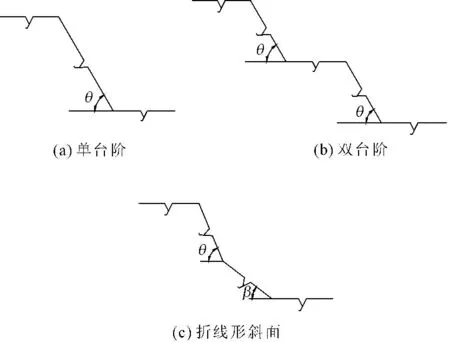
图2 台阶状复杂地基

2 加固方案

根据工程经验，为了研究锚索设计参数对导流墙侧向抗滑稳定的影响，确定导流墙预应力锚索加固[9-10]的具体形式，对以下12个加固方案进行计算分析：

方案1：导流墙内不施加锚索；

方案2～方案4：导流墙右侧面上Ⅰ号锚索高程为1 770.0 m，锚固角α分别取20°、30°、40°，锚固间距4.0 m，L=2.0 m，见图3、图4。

方案5～方案7：导流墙右侧面上Ⅰ号锚索高程分别取为1 770.0 m、1 766.0 m、1 762.0 m，锚固角20°，锚索间距4.0 m，L=2.0 m，见图3、图4。

方案8～方案10：导流墙右侧面上Ⅲ号锚索高程为1 754.0 m，锚索间距分别取3.0 m、4.0 m、5.0 m，锚固角20°，L=2.0 m，见图3、图4。

方案11～方案13：导流墙右侧面上Ⅰ号锚索高程为1 770.0 m，L分别取2.0 m、3.0 m、4.0 m，锚固角20°，锚固间距4.0 m，见图3、图4。

图3 导流墙预应力锚索加固示意图

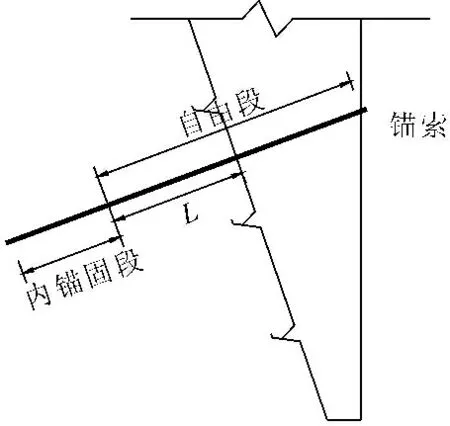
图4 预应力锚索示意图

3 计算分析

3.1 计算方法

(1) 对于折线形台阶状复杂地基(见图2)，其抗滑力及滑动力采用分段求和的计算方法[11]：

(1)

s=∫∫τidA

(2)

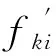
地基斜面上抗滑力及滑动力按式(1)、式(2)乘以相应斜面与水平面倾角θ的余弦值，进行正交分解即可。

最终将各面的抗滑力及滑动力求和，即为总抗力及总作用效应。

(2) 导流明渠的导流墙侧向抗滑稳定计算采用承载能力极限状态法来判断其抗滑稳定，基本组合承载能力极限状态设计表达式[12]为：

(3)

式中：γ0结构重要性系数，结构安全级别为Ⅱ级，取1.0；ψ设计状况系数，此次计算取0.95；S(·)作用效应函数；R(·)抗力函数；γG永久作用分项系数；γQ可变作用分项系数；Gk永久作用标准值；Qk可变作用标准值；αk几何参数的标准值；fk材料性能的标准值；γm材料性能分项系数，摩擦系数f′的分项系数为1.3，黏聚力c′的分项系数为3.0；γd1基本组合结构系数，此次计算取1.2。

(3) 有限元计算中，施加在锚索上的预应力可采用等效荷载法、初始应变法和降温法进行模拟，初始应变法和降温法计算精度更高。文中采用降温法模拟预应力，此法比较简单，同时可以模拟预应力的损失。降温值可根据预应力锚索弹性模量、膨胀系数和预应力计算得到，计算公式为[13]：

(4)

式中，ΔT为降低温度，℃；F为预应力，kN；a为膨胀系数，mm/(mm·℃)；E为预应力筋弹性模量，GPa；S为预应力筋截面积，mm2。

本例中采用的预应力锚索膨胀系数为1.0×10-5mm/(mm·℃)，弹性模量210 GPa，单根锚索直径100 mm(单根截面面积7 850 mm2)，设计预应力2 000 kN，采用平面有限元进行分析时，将预应力在垂直纸面方向进行均化，即预应力/锚索垂直纸面间距=2000/4.5=444.44 kN。由于施加预应力的过程中，混凝土和地基会发生压缩变形，使得有效预应力水平比预计值要低，因此有限元计算中施加在锚索上的预应力水平所对应的温度要比按式(4)计算的温度略大一些，如降温值=-444.44/(10-5×210×7850)=-26.96℃，以此值为初值，使结构只在重力作用下，模拟自重作用下结构的压缩变形，通过试算提取锚索上实际预应力值，确定最终的降温值为-27.5℃，对应的实际预应力为449.8 kN。

3.2 计算假定

平面有限元计算中，计算假定如下：

(1) 导流墙以及地基材料均满足弹性力学基本假定，即连续、完全弹性、均匀、各向同性以及小变形假定，属于线弹性问题，可以采用叠加原理。

(2) 导流墙与地基连接可靠，不存在相互脱离、相互碰撞的情形，即满足连续性条件，不考虑接触非线性。

3.3 计算模型

采用ANSYS有限元软件[14]对导流墙预应力锚索加固进行模拟计算，导流墙所选基础范围为向左、右岸和深度方向各延伸50 m，导流墙与地基采用平面四节点单元Plane42模拟，锚索采用杆单元Link8进行模拟，锚索杆单元与导流墙，地基单元采用共节点的连接形式。建基面高程以下基础左右边界分别按法向约束，基础底部边界采用全约束，脱离建基面部位按自由边界处理。

有限元分析模型中坐标系采用直角坐标系，选取的坐标方向如图5所示：Z正方向为指向上游，Y正方向为竖直向上，X正方向指向厂房坝段。整体有限元模型及导流墙加预应力锚索模型见图5、图6。

3.4 计算结果分析

结果分析中，因采用承载能力极限状态法判断抗滑稳定，所以将总抗力与总作用效应的差值Δ定义为抗滑稳定安全富裕度，差值Δ越大越安全。此外，表1～表4中以II号锚索为例列出了锚索上模拟的预应力。

图5 整体有限元模型

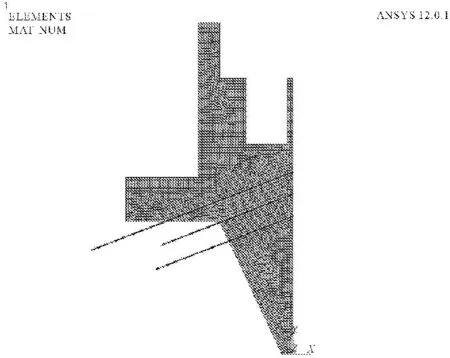
图6 导流墙预应力锚索加固模型

(1) 不同锚固角下，锚固效应的计算结果分析

锚固角对导流墙侧向抗滑稳定的影响见表1。

表1 不同锚固角的锚固效果

注：α为锚索与水平线的夹角。

从计算结果分析可知：方案1与方案2～方案4对比加斜向锚索对导流墙的侧向抗滑稳定起到了加固作用，此外锚固角α越小，对导流墙的抗滑稳定越有利，锚固角α由20°～40°变化，虽说总抗力在增大，但是总的作用效应也随之增大，反而最终两者的差值在减小，也就是说安全富裕度在减小。

(2) 不同锚固高程下，锚固效应的计算结果分析

锚固高程对导流墙侧向抗滑稳定的影响见表2。

表2 不同锚固高程的锚固效果

从计算结果分析可知：方案1与方案5～方案7对比加斜向锚索对导流墙的侧向抗滑稳定起到了加固作用，并且随着Ⅰ号锚索在导流墙右侧面上锚固位置降低，预应力锚索(Ⅰ～Ⅲ号锚索)在基础斜面上作用范围的加大，对导流墙侧向抗滑稳定越有利，Ⅰ号锚索高程由1 770.0 m下降到1 762.0 m，总抗力与总作用效应的差值Δ增大154.08 kN，增大幅度十分明显。

(3) 不同锚固间距下，锚固效应的计算结果分析

锚固间距对导流墙侧向抗滑稳定的影响见表3。

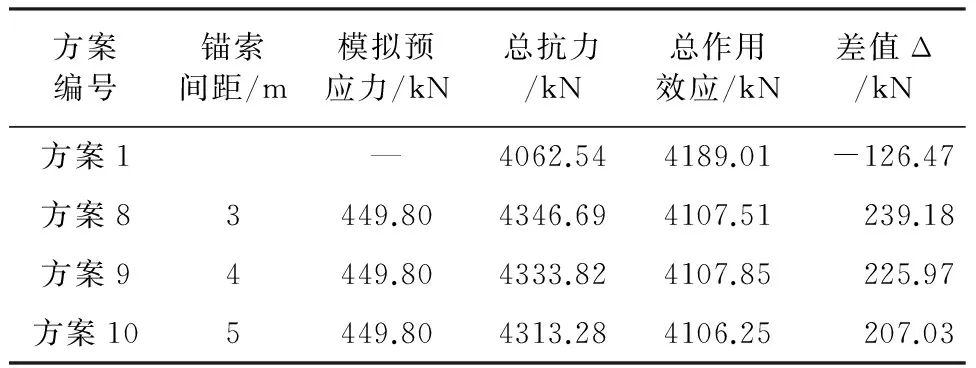
表3 不同锚固间距的锚固效果

从计算结果分析可知：方案1与方案8～方案10对比加斜向锚索对导流墙的侧向抗滑稳定起到了加固作用，并且随着锚固间距由3.0 m～5.0 m变化，锚固间距越大，总抗力与总作用效应的差值Δ越小，安全富裕度越小，即就是说锚固间距越小对导流墙的侧向抗滑稳定越有利。

(4) 不同内锚固段长度下，锚固效应的计算结果分析

采用锚索地基内自由段长度L的变化，间接反映内锚固段长度对导流墙侧向抗滑稳定的影响，计算结果见表4。

表4 不同内锚固段长度的锚固效果

从计算结果分析可知：方案1与方案11～方案13对比加斜向锚索对导流墙的侧向抗滑稳定起到了加固作用，但内锚固长度的变化对导流墙侧向抗滑稳定的影响甚微。查阅相关文献，对于内锚固段长度最为关心的是锚索在承受预应力时，内锚固段不会被拔出。根据李家峡、漫湾、紫坪埔等边坡锚固现场试验证明：Ⅲ类围岩以上的较坚硬岩石中，4 m～5 m的内锚固段长度总可以承受3 000 kN的预应力[15]。本例Ⅲ围岩，设计预应力2 000 kN，内锚固长度10 m以上，因此不会出现被拔出现象。

4 结 论

通过以上的方案对比，现对锚索设计参数对复杂地基上导流墙侧向抗滑稳定的影响总结如下：

(1) 在施工条件允许的情况下，锚固角应尽量与水平线呈小角度布置，锚索间距越小越有利；

(2) 对于这种台阶状地基上的导流墙，锚固高程的变化对导流墙侧向抗滑稳定影响特别显著，台阶斜面上锚固范围的加大起到了决定性作用，因此加固时应重视斜面上锚索的布置；而内锚固段长度变化影响甚微；

(3) 最终复杂地基上导流墙加固形式为：考虑群锚效应，锚索长短错开布置，导流墙右侧面上Ⅰ号锚索高程为1 760.0 m，锚索间距3.0 m，锚固角α=20°，地基内自由段长度L=2.0 m。

[1] 陈祖煜，杨 健.岩土预应力锚固技术的进展[J].贵州水力发电，2004，18(5)：5-6.

[2] 李兰秀，魏 晶.桥巩水电站纵向导墙基岩预应力锚索设计[J].红水河，2012，31(6)：1-4.

[3] 杨春光.桥巩船闸闸室左边坡预应力锚索设计与施工[J].水电与新能源，2012(1)：51-53.

[4] 张发明，刘 宁，赵维炳,等.岩质边坡预应力锚固的优化设计方法[J].岩土力学，2002，23(2):117-118.

[5] 李 宁，张 平，李国玉.岩质边坡预应力锚固的设计原则与方法探讨[J].岩石力学与工程学报，2004，23(17):2972-2976.

[6] 林兴超，汪小刚，陈文强，等.边皮锚固与加固协调作用机制研究[J].岩石力学与工程学报，2014，33(增1)：3123-3128.

[7] 邓宗伟，冷伍明，邹金锋，等.预应力锚索荷载传递与锚固效应计算[J].中南大学学报：自然科学版，2011，42(2):501-507.

[8] 詹筱霞，罗 罡.预应力锚索在坝基抗滑稳定中的应用研究[J].江西理工大学学报，2014，35(1):54-59.

[9] 中国人民共和国水利部.SL 212-98水工预应力锚固设计规范[S].中国水利水电出版社.

[10] 林继镛.水工建筑物[M].北京：中国水利水电出版社，2006.

[11] 陈 演.重力坝安珀坝段抗滑稳定及横缝工作状态研究[D].西安：西安理工大学，2014.

[12] 中国人民共和国国家经济贸易委员会.DL5108-1999混凝土重力坝设计规范[S].北京：中国电力出版社，1999.

[13] 张社荣，祝 青，李 升.大型渡槽数值分析中预应力的模拟方法[J].水力发电学报，2009,28(3):97-100.

[14] 李 围.Ansys土木工程应用实例[M].北京：中国水利水电出版社，2007.

[15] 蒋锁红，林 鹏，郑文炜，等.李家峡拱坝大吨位锚索内锚固段岩体变形分析[J].水力发电学报，2011，30(5):163-169.

Influence Analysis of the Design Parameters of Anchor Cable on the Diversion Wall Reinforcement with Prestressed Anchorage on Complicated Foundations

BI Chenxi, LI Shouyi

(InstituteofWaterResourcesandHydro-electricEngineering,Xi’anUniversityofTechnology,Xi’an,Shaanxi710048,China)

Prestressed anchor cable have been widely used as a main reinforcement method in many project cases, meanwhile, it’s also an important approach to improve the stability of structures. According to the ANSYS simulation, prestressed anchor cables were adopted to reinforce the diversion wall on a complicated foundation. the influence of design parameters of the anchor cables was studied in detail. In view of the stepped complicated foundation, the arrangement of the anchor cables was put forward. The results indicate that the design parameters of anchor cables have different effects on the diversion wall reinforcement with prestressed anchorage on complicated foundations, the lateral anti-sliding stability of the diversion wall is extremely sensitive to the change of the anchorage angle, altitude and interval space of the anchors, with the anchorage altitude posing the most significant impact on the anchoring effects.

prestressed anchor cable; design parameters; diversion wall; the value of temperature decrease

10.3969/j.issn.1672-1144.2015.05.028

2015-05-17

2015-06-21

毕晨曦(1989—)，男，陕西蓝田人，硕士研究生，研究方向为水工结构应力仿真分析。E-mail:1136687560@qq.com

李守义(1955—)，男，甘肃庄浪人，教授，博导，主要从事水工结构应力仿真分析及结构优化设计方面的教学与科研工作。 E-mail:lishouyi@126.com

TU472

A

1672—1144(2015)05—0141—05