CFRP布加固混凝土矩形短柱轴压性能分析

贾 良，聂红宾

(陕西铁路工程职业技术学院 轨道工程系， 陕西 渭南 714000)

CFRP布加固混凝土矩形短柱轴压性能分析

贾 良，聂红宾

(陕西铁路工程职业技术学院 轨道工程系， 陕西 渭南 714000)

为了进一步研究碳纤维(Carbon Fiber Reinforced Polymer,CFRP)加固混凝土短柱轴心受压力学性能,根据合理拱轴线、应力公式及混凝土强度模型，推导出CFRP布加固柱修正后的抗压承载力公式，并通过理论计算和ABAQUS有限元分析验证公式的正确性。

CFRP布；有效约束系数；承载力公式；ABAQUS

CFRP用于结构加固开始于80年代美、日等发达国家,1993年在温哥华召开了第一届FRP增强钢筋混凝土结构的国际会议[1]。瑞典的Meier首次用CFRP布加固桥梁;Saadamanesh & Ehsani和Ritchie对CFRP布加固构件进行了深入的研究。由于CFRP布加固柱能充分发挥材料的优势,减小截面尺寸,增大延性,提高构件的抗震性能,国内学者赵国藩、吴智深、吕西林等人分别对CFRP布加固技术做了深入研究[2-4],主要研究了碳纤维布的用量、加固区段范围、加固形式、CFRP布端部锚固以及加固前构件的荷载作用等参数,但对CFRP布的有效约束系数和承载力提高系数研究较少,本文在已有研究成果的基础上,通过理论计算和ABAQUS有限元模拟的方法,对CFRP布加固矩形短柱轴压力学性能进行研究。

1 基本假定

本文在已有参考文献的基础上[5-6],列出如下基本假定:

(1) 计算柱受压面积时,不考虑CFRP布的厚度;

(2) CFRP布粘贴良好,粘结端不会发生剥离破坏;

(3) 柱破坏时,CFRP布达到极限抗拉强度。

2 CFRP布加固混凝土矩形柱承载力计算

2.1 混凝土柱承载力公式

《混凝土结构设计规范》[7](GB50010-2010)规定了柱的轴心受压承载力公式为：

(1)

2.2 CFRP布加固柱的承载力公式

CFRP布加固柱的承载力由三部分组成:纵向钢筋的承载力、非约束区混凝土的承载力和有效约束区混凝土的承载力[8]。本文主要研究CFRP布约束混凝土柱的承载力提高率,为了避免钢筋对加固柱的影响,计算中不计钢筋的承载力,因此,可得出承载力的计算公式:

Nu=0.9φ(fcA1+α′fcA2)

(2)

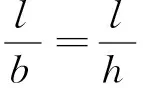
2.2.1CFRP布的约束系数

CFRP布约束柱受到轴向压力时,混凝土会发生侧向变形,由于CFRP布的包裹,侧向变形受到约束,产生侧反力,侧反力由表到内,随之增大,中间的混凝土受力最大,由于矩形柱的形状特异,产生的反力呈拱形(见图1),拱形内的混凝土受到约束很小,可忽略不计,因此,在柱内部会形成约束区和非约束区,为方便推导,引入CFRP布对混凝土的约束系数为：

(3)

式中，φ1为混凝土约束系数。

图1 混凝土约束区域

根据图2可知,约束区的混凝土受力均匀,且截面呈拱形,合理拱轴线的方程为：

(4)

式中：H为CFRP布的水平约束力；q为竖向均布荷载；x为任意截面到拱角的距离；y为拱平面方程式。

图2 应力模型

当拱轴线的夹角为45°时,可得水平力公式：

(5)

式中：h为柱的高度。

于是可得到合理水平拱截面公式为：

(6)

同理,竖向拱平面方程为：

(7)

式中：b为柱宽度。

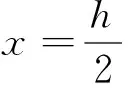
拱形的截面面积为：

(8)

式中：l为拱的底长；h为拱高。

有效约束面积的计算式为：

(9)

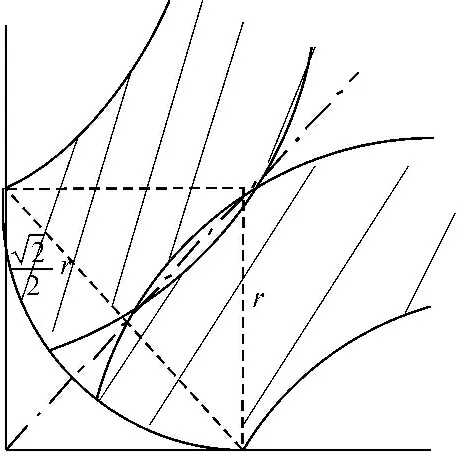
图3 柱角细部图

弧长计算式为：

(10)

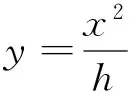
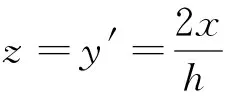
(11)

将式(11)代入式(10)中,得：

(12)

经过积分可得弧长为：

l=1.479h

(13)

因为上下都有倒角,同理,也得到沿宽度方向倒角弧长为：

l=1.479b

(14)

根据式(10)～式(14),可得因倒角产生的约束面积为：

(15)

经过以上推导,可得出有效约束系数为：

(16)

在本文中主要讨论有效约束系数简化公式(16)。

2.2.2 约束柱承载力提高系数

CFRP布约束柱承载力的提高首先取决于CFRP布的抗拉强度。在一定的范围内,CFRP布的抗拉强度越大,承载力的提高越高;其次,CFRP布加固柱承载力的提高与柱的几何形状有关,大量实验证明CFRP布加固圆形柱的承载力提高是最明显的,矩形柱中的方形柱承载力效果最好;再次,承载力的提高还与被约束混凝土的强度有关,混凝土的强度越高,CFRP布加固效果越不明显;最后,承载力的提高还与有效约束系数有关,即与倒角半径有关,倒角半径越大,承载力的提高越大,反之亦然。

学者XIAOY认为加固柱的承载力主要取决于CFRP布的侧向约束刚度[10],侧向刚度为：

(17)

式中：El为侧向约束刚度；Ef为CFRP的弹性模量；D为等效圆直径；s和s1分别为条带宽度及间距；t为CFRP布的厚度。

学者Karbhari,V.M提出的有效约束混凝土强度模型[11]为：

(18)

本文根据式(15)代入式(16),可得公式为：

(19)

对式进行简化,可得承载力提高系数，令

(20)

根据式(20)分析可知,承载力的提高系数与柱的几何尺寸成反比,截面的高和宽对承载力提高影响相同；与CFRP布的极限抗拉强度、厚度和有效约束系数成正比。

根据以上推导,可得出CFRP布加固混凝土柱的承载力公式,

(21)

2.3 算例验算

(1) 抛物面约束区域面积

(2) 倒角产生约束面积

(3) CFRP布的有效约束面积

(4) 有效约束系数

倒角半径产生的影响系数φ1=21.233

在不同加固方式下,CFRP布的有效约束系数α′,见表1。经计算,不同加固方式的承载力见表2。

表1 有效约束系数α′

表2 承载力的理论计算值

3 ABAQUS有限元模拟

本文采用ABAQUS有限元软件对试件进行非线性分析,混凝土模型采用规范(GB50010-2010)中混凝土的本构关系模型,此模型属于脆性破裂模型,适用于做静力分析,需要设定的参数较少,局限性是收敛性比较差。CFRP布的极限抗拉强度为1 530MPa,分别建立CFRP布和混凝土柱的模型,进行组合,为简化模型分析,采用ABAQUS/Standard对CFRP布加固构件进行分析,划分网格长度10mm,CFRP布与混凝土表面之间作用力设为固定,无相对位移,柱顶上施加恒定轴力,通过位移加载的方式施加在柱顶,加载方式采用位移控制,其操作步骤见图4[12-15]。

3.1 建立模型

采用ABAQUS/Standard对柱进行建模和网格划分,分别得到CFRP布加固混凝土柱的全包、分包模型。

3.2 模拟结果

本文采用位移加载,CFRP布加固混凝土柱达到最终破坏,应力云图见图5～图11,在图5中,未加固柱首先在柱顶角处达到破坏,其次,柱中间应力较大,破坏形态呈棱锥形。两端分包柱破坏时,CFRP布加固顶端应力最大,混凝土在粘贴CFRP布的下角处也发生破坏,破坏呈灯笼状,如图6和图10所示。中间分包柱的破坏位置在混凝土柱的顶角和CFRP布中间段,如图7和图11所示。在图8和图9中,全包加固柱的破坏位置在CFRP布的顶角和混凝土的中心区域。

图4ABAQUS步骤流程图

4 实验结果对比

AQBAQS模拟值和理论计算值进行对比,如表3所示,图12为ABAQUS软件模拟CFRP布加固柱的荷载与竖向位移曲线。CFRP布加固混凝土柱承载力均有提高,两端分包承载力提高最明显,最经济,但不同计算方式下,未加固柱误差较小,两端分包误差较大。

表3 承载力对比表

加固方式承载力/kN计算值试验值ABAQS值误差(计算值为标准)/%试验值ABAQS值未加固270.000279.848282.3263.654.57全包357.858335.889328.022-6.14-8.33两端分包313.928335.133274.9846.75-12.41中间加固313.928322.654319.1452.781.66

图12 模拟荷载与竖向位移曲线

通过以上分析,可得如下结论：

(1) 根据AQBAQS的应力云图可知,加固柱破坏主要发生在应力集中区;

(2)AQBAQS能较好模拟CFRP布加固混凝土柱的荷载——竖向位移曲线;

(3) 对模拟结果对比分析,承载力的理论值和模拟值之间存在1.66%～12.4%的误差,误差值平均在6%左右,较好的验证了理论公式的正确性。

5 结 论

(1) 利用合理拱轴线理论,推导了CFRP布加固混凝土柱的有效约束系数,同时根据约束系数公式得出了加固技术中倒角的重要性;根据混凝土的本构关系,推导出新的承载力提高系数;在有效约束和承载力提高系数的基础上,得出了CFRP布加固混凝土柱的轴心受压承载力公式。

(2) 利用ABAQUS对CFRP布加固柱进行模拟,分析了加固柱的破坏形态、荷载与跨中挠度的关系,得到了加固柱的应力云图以及不同加固方式下柱的承载力模拟值。

(3) 通过对承载力的理论值和模拟值进行对比,理论值和模拟值之间平均存在6%的误差,吻合良好。

[1] 吴 刚,吕志涛.纤维增强复合材料(FRP)约束混凝土矩形柱应力-应变关系的研究[J].建筑结构学报，2004,25(3):99-106.

[2] 周 乐,王元清,施 刚，等.钢梁外包FRP混凝土抗弯承载力计算[J].沈阳建筑大学学报：自然科学版，2014,30(2):193-200.

[3] 李世宏,孙永新.采用预应力碳纤维布加固的必要性及国内外研究状况[C]//2005全国FRP与结构加固学术会议论文精选,2005.

[4] 赵 彤,谢 剑,戴自强.碳纤维布提高钢筋混凝土梁受剪承载力试验研究[J].建筑结构,2000，30(7):21-25.

[5] 赵海波.CFRP加固高强混凝土柱轴心受压性能试验研究[D].大连：大连理工大学,2006.

[6] 刘 涛.碳纤维(CFRP)布加固混凝土矩形柱的性能研究[D].上海：上海大学,2006.

[7] 中华人民共和国住房和城乡建设部.GB50010-2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.

[8] 魏 华.CFRP加固局部强度不足混凝土柱受压力学性能研究[D].大连：大连理工大学，2009.

[9] 贺宪成.二次荷载作用下CFRP加固混凝土矩形柱受压性能研究[D].上海：同济大学,2005.

[10] XIAO Y, WU H. Compressive behavior of concrete confined by carbon fiber composite jackets[J]. Journal of Material in Civil Engineering. ASCE, 2000,12(2):139-146.

[11] Karbhari V M, Gao Y. Composite jacketed concrete under uniaxial compression verification of simple design equations uniaxial[J]. Journal of Material in Civil Engineering, 1997,9(4):185-193.

[12] 吴汉升.横向包裹CFRP布加固混凝土柱试验研究及有限元分析[D].北京：中国地震局工程力学研究所,2010.

[13] 翟爱良,孙明杰，季昌良，等.预应力CFRP布加固混凝土大偏心受压柱试验研究[J].水利与建筑工程学报，2013，11(1):31-36.

[14] 聂红宾.CFRP布加固冻融损伤混泥土力学性能分析[D].沈阳：沈阳大学,2013.

[15] 周 乐,聂红宾.CFRP布加固钢筋混凝土梁黏结应力分析[J].沈阳大学学报：自然科学版，2013,25(1):72-75.

Study on the Axial Behavior of Rectangular Concrete Columns Strengthened with CFRP Sheets

JIA Liang, NIE Hongbin

(RailwayEngineeringDepartment,ShaanxiRailwayInstitute,Weinan,Shaanxi714000,China)

In order to further understand the mechanical properties of carbon fiber reinforced polymer(CFRP) reinforced concrete short columns under axial compression, the study on the bearing capacity formula of the columns was carried out. According to the reasonable arch axis, stress formula and the concrete strength, the revised bearing capacity formula of the CFRP sheet reinforced column was deduced and then verified with theoretical calculation and ABAQUS finite element analysis.

CFRP sheets; effective constraint coefficients; the formula of bearing capacity; ABAQUS

10.3969/j.issn.1672-1144.2015.05.030

2015-05-10

2015-06-13

贾 良(1982—)，男，山西平鲁人，硕士，讲师，主要从事土木建筑工程方向教育与研究工作。E-mail:styjialiang@163.com

TU398+.9

A

1672—1144(2015)05—0151—05