基于SPH深度积分模型的滑坡数值分析

陶言祺，李家钢

(1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024;2.中海油研究总院, 北京 100081)

基于SPH深度积分模型的滑坡数值分析

陶言祺1，李家钢2

(1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024;2.中海油研究总院, 北京 100081)

滑坡会对工程结构物造成严重破坏,滑移速度和距离是量化和分析滑坡的两个重要参数。针对滑移速度和距离预测一直比较复杂的现状,建立考虑土体固结和侵蚀效应的控制方程,选用摩擦流变模型,采用SPH深度积分算法,对滑坡进行了模拟研究。对比不同坡度、接触摩擦系数和侵蚀率条件下的滑移体速度、长度的时程曲线,分析不同条件下滑移体的最终沉积形态,整理了最大滑移距离和速度,讨论其变化规律。研究成果可为滑坡灾害预警提供技术参考。

滑移速度；SPH深度积分法；摩擦流变模型；侵蚀效应

滑坡是一种常见的地质灾害,广泛分布在山区、河谷地带,危害很大。国内外对于滑坡的研究主要集中在诱发机制、失稳分析、灾害评估等方面。由于地震、暴雨、人类活动影响等造成的滑坡每年都造成巨大的经济损失和人员伤亡。因此,研究滑坡对于工程设计和防灾减灾具有重要意义。

针对滑坡[1]问题,国内外学者多采用SPH法[2]、离散单元法[3]、无网格伽辽金法[4]、细胞自动机法[5]、非连续变形分析方法[6]等方法进行研究,并取得了一定研究成果,但是针对滑移速度和距离的计算一直是比较复杂的问题[7]。Pastor等[8]采用SPH深度积分法,考虑土骨架与孔隙流体的动力耦合和侵蚀效应,建立了耦合孔隙水压力的深度积分模型。依据Biot-Zienkiewicz方程的u-p格式进行积分,将流动-固结方程简化成耦合孔压的深度积分方程。二维深度积分模型能够简便、准确地计算任意时刻滑移体的滑移速度、高度和滑移距离等。Pastor等用SPH深度积分法对山体滑坡、泥石流等问题进行了一系列研究和验证,对香港青山滑坡和加拿大Frank滑坡进行了模拟[9-10],结果显示SPH深度积分法能够较为精确地模拟陆地滑坡问题,同时计算效率高。

综上所述,本文基于二维SPH深度积分法,建立了滑坡模型,并考虑土骨架和孔隙流体的动力耦合,主要分析了坡度、滑移体与坡床间的接触摩擦系数以及侵蚀率对滑移距离和速度的影响。

1 基本理论

滑坡过程中需要考虑滑移体的自重作用、摩擦作用,且被侵蚀、挟带的土体的惯性阻力会增加滑移体底部的剪切阻力[11]。

1.1 SPH深度积分模型

SPH深度积分法通过以下公式得到离散化的深度积分方程。函数的近似逼近：

(1)

式中：φ(xj)是空间变量xj的函数；插值核函数Wij=W(xj-xi，hsml)，常采用三次样条曲线插值格式[12]，hsml为光滑长度；mj为质量；ρj为密度。

深度积分公式：

(2)

式中：φi(x3)是沿深度方向变量x3的函数，[z,z+h]为x3的积分区间。

在控制方程的简化过程中,假定流体各项同性、孔隙流体不可压缩,在土骨架中的流动满足达西定律,忽略孔隙水相对于土骨架的加速度;滑移体为饱和土体,其自由面为排水面;滑移速度可以分解成滑动速度和渗流速度,土体固结由渗流速度决定。

(1) 准拉格朗日格式控制方程

质量守恒方程:

(3)

动量守恒方程：

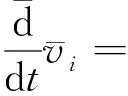
(4)

竖直向固结方程：

(5)

式中：hi为各滑移条块的高度；mj=Ωjhj，为虚拟质量，Ωj各滑移条块底面积；vij=vi-vj，vj为各滑移条块的深度平均速度；er体积增长率；gradWij为插值核函数Wij的梯度值；Pi为孔隙水压力；σi为应力张量，以拉应力为正；b为体加速度；Nb为坡面空间梯度值；tb为作用于滑移体底面的应力；P1i为超孔隙水压力；cv为土体的渗透固结系数。

(2) 摩擦流变模型

基于SPH深度积分法,Pastor引入一系列流变模型,并进行了修正[9，13]。成果表明,土体沿坡面滑动过程中,需要考虑摩擦作用,并对摩擦进行线性动量修正。根据Coulomb摩擦理论,滑移体与坡面接触位置，摩擦引起的包含超孔隙水压力项的剪应力为：

(6)

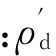
(3) 侵蚀准则

Pastor等引入了Hungr侵蚀定律[11]模拟侵蚀：

(7)

式中：Er为侵蚀率；V0和Vf分别为滑移体的初始和最终体积;l为流径的长度。

1.2 SPH深度积分法的求解方法

SPH深度积分法采用显示四阶Runge-Kutta法求解。滑移条块受自重、摩擦作用、被侵蚀土体的惯性阻力,定义总作用为：N=Nin+Nex。

滑移条块间的相互作用Nin：

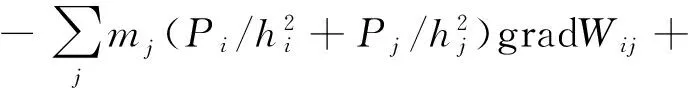
(8)

自重、摩擦作用、侵蚀作用之和Nex为：

(9)

为保证解的收敛性,时间步长[12]设定为：

(10)

式中：Δl为质点间的间距；g为重力加速度；h为滑移体最大高度。

滑移速度和距离的计算公式为：

(11)

(12)

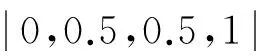
2 SPH深度积分法模拟滑坡

滑移体沿坡度为θ的斜坡滑动,滑移体密度ρ为1 800 kg/m3,接触摩擦系数tanφb为0.1～0.29[10],甚至更小[14-15];侵蚀率Er为0～1×10-4/m[16]；渗透固结系数cv设为2.71×10-4m2/s[16]；重力加速度取为9.8 m/s2。

滑坡示意图如图1所示,水平方向为x方向,z坐标竖直向上。坡面采用整体坐标系定义,斜坡段水平长度为12 000 m,水平缓冲段长度为5 000 m。土条高度h采用相对坐标,即为相对坡面的高度。滑移体的初始形状通过多组(x，h)坐标定义为对称型抛物线,沿坡面长度为280 m,最大高度为11 m。对滑移体进行剖分,其中滑移体沿x方向等分150份。定义滑移体的最大高度为hmax、前后端的水平距离为滑移体长度L,滑移体前端的滑移距离为D、前端速度为vf。

图1 滑坡示意图

3 数值计算与对比分析

依据上述理论,对不同工况下的陆地滑坡进行数值模拟,讨论相关参数的变化对滑坡的影响。

3.1 坡度对滑坡的影响

在接触摩擦系数tanφb=0.1、侵蚀率Er=0时,分别针对坡度θ=1°、5°、10°、13°、14°、15°六种工况进行模拟,结果见图2、图3。

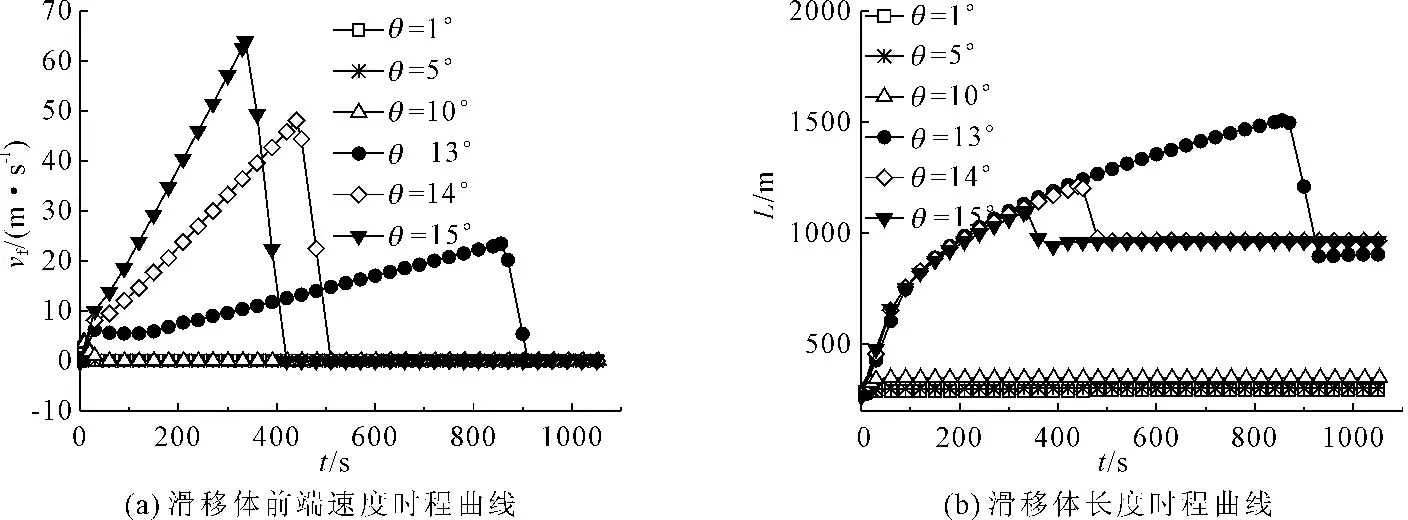
图2 坡度对滑坡的影响

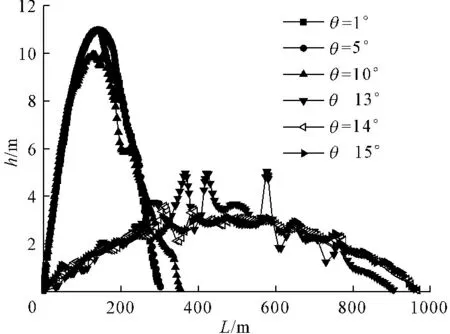
图3 滑移体最终沉积形态

结果表明,坡度为1°、5°、10°三种工况下,仅滑移体的前端发生小距离的滑动,后端没有滑动,滑坡很快停止,沉积形态与初始形态基本一致;坡度为13°、14°、15°三种工况下，滑移体发生了完全滑动,同时随着坡度的增大,最大滑移距离和速度均增大,但在缓冲段沉积高度和长度非常接近。坡度为13°时,沉积物顶部波动较明显。

3.2 接触摩擦系数对滑坡的影响

在坡度θ=15°、侵蚀率Er=0时,分别设定初始接触摩擦系数tanφb=0.1、0.105、0.11、0.115、0.12,对五种工况进行计算,结果如图4、图5所示。由图4(a)可见,滑移体在斜坡段上加速滑动时,最大速度和加速度随接触摩擦系数的增大而减小。一旦进入缓冲段减速时,加速度基本相同。由图4(b)和图5可知,前四种工况,在进入缓冲段之前,滑移体长度随时间的变化规律基本一致,最终沉积形态也基本一致。当tanφb=0.12时,滑移体滑动约670 m后在斜坡段上停止,未进入缓冲段,滑移体后端堆积非常明显。综合分析表明,接触摩擦系数较为敏感,其参数变化对滑坡的最大滑移速度和距离影响很大。

图4 摩擦系数对滑坡的影响

图5 滑移体最终沉积形态

3.3 侵蚀率对滑坡的影响

滑移体侵蚀坡面,并挟带土体共同滑移。接触摩擦系数tanφb=0.1、坡度θ=15°时，分别针对侵蚀率Er=0、10-7/m、10-6/m、10-5/m、10-4/m五种工况进行计算,图6给出了vf、L随时间的变化曲线。当侵蚀率为0、10-7/m、10-6/m时,vf-t、L-t曲线基本重合,前端滑移距离也非常接近,说明侵蚀率小于10-6/m时,侵蚀效果不明显。由图6、图7可见，当侵蚀率增大至10-5/m时,滑移体最大沉积高度和长度均比前三种工况大。计算结果显示侵蚀率为10-4/m时,滑移体最终沉积高度为10.12 m,接近初始高度;沉积长度为1 019 m,约为初始长度的4倍,滑移体体量明显增大,说明滑移体对坡床发生了显著侵蚀。

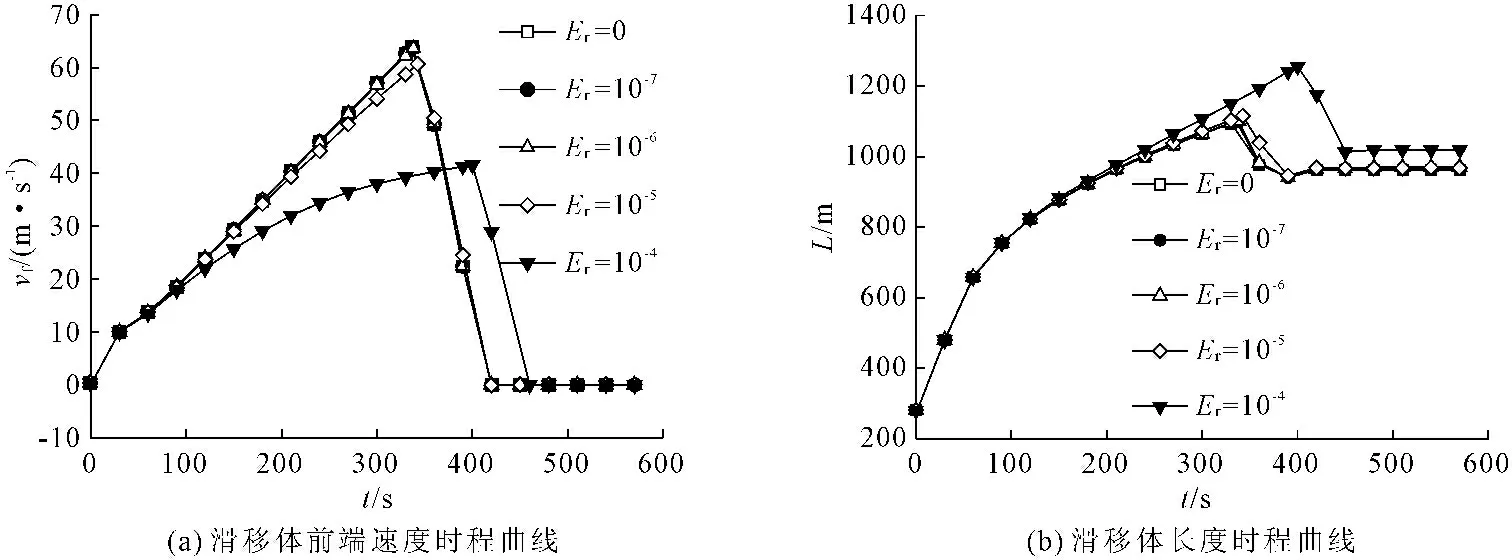
图6 侵蚀率对滑坡的影响

图7 滑移体最终沉积形态

由于被侵蚀土体的初始动量为零,根据动量守恒可知,滑移体的加速度随着体量的增大而减小。因此,侵蚀率越大,滑移体的最大滑移距离和速度越小。

4 结 论

通过SPH深度积分法对不同工况的滑坡进行了数值模拟,并讨论了最大滑移距离和速度及最终沉积形态的影响因素。分析表明：

(1) 当坡度低于10°时,未发生整体滑动。随着坡度的增长,滑移体发生整体滑动,同时随着坡度的增大,最大滑移距离和速度均增大,但坡度变化对最终沉积形态影响较小；

(2) 接触摩擦系数比较敏感,其参数变化对滑坡的最大滑移距离和速度影响很大；

(3) 当侵蚀率达到10-4/m以上时,侵蚀效应明显,滑移体的最大滑移距离和速度减小,但滑移体体量明显增大；

(4) 建立的SPH深度积分模型能够考虑滑移体滑移过程中土体固结和侵蚀效应,计算滑移速度和距离简便,适于模拟滑坡。

[1] 郝明辉，许 强，杨 磊，等.滑坡-碎屑流物理模型试验及运动机制探讨[J].岩土力学，2014，35(S1):127-132.

[2] 黄 雨，郝 亮，谢 攀，等.土体流动大变形的SPH数值模拟[J].岩土工程学报，2009，31(10):1520-1524.

[3] 申 通，王运生，吴龙科.重庆小南海滑坡形成机制离散元模拟分析[J].岩土力学，2014，35(S2):667-675.

[4] Arimoto S, Murakami A. Characteristics of localized behavior of saturated soil by EFG[C]//Proceedings of 1st International Workshop on New Frontiers in Computational Geomechanics, Banff, 2002：169-172.

[5] Baxter G W, Behringer R P. Cellular automata models of granular flow[J]. Physical Review A, 1990,42(2):1017-1020.

[6] Sasaki T, Ohnishi Y, Yohinaka R. Discontinues deformation analysis and its application to rock mechanics problems[J]. Journal of Geotechnical Engineering, JSCE, 1994，Ⅲ-27:11-20.

[7] 秦 云，姜清辉，郭慧黎.滑坡速度预测的计算方法探讨[J].岩土力学，2008,29(S1):373-378.

[8] Pastor M, Haddad B, Sorbino G, et al. A depth-integrated coupled SPH model for flow-like landslides and related phenomena[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2009,33:143-172.

[9] Pastor M, Blanc T, Pastor M J. A depth-integrated visco-plastic model for dilatant saturated cohesive-frictional fluidized mixtures: Application to fast catastrophic landslides[J]. Journal of Non-Newtonian Fluid Mechanics, 2009,158:142-153.

[10] Thomas Blanc. Numerical simulation of debris flows with the 2D-SPH depth integrated model[D]. Vienna, University of Natural Resources and Applied Life Sciences, 2008.

[11] Pirulli M, Pastor M. Numerical study on the entrainment of bed material into rapid landslides[J]. Geotechnique, 2012,62(11):959-972.

[12] Monaghan J J, Gingold R A. Shock simulation by the particle method SPH[J]. Journal of Computational Physics, 1983,52:374-389.

[13] Pastor M, Quecedo M, Gonzalez E, et al. A simple approximation to bottom friction for Bingham fluid depth integrated models[J]. Journal of Hydraulic Engineering ASCE, 2004,130(2):149-155.

[14] McDougall S, Hungr O. A model for the analysis of rapid landslide motion across three-dimensional terrain[J]. Canadian Geotechnical Journal, 2004,41:1084-1097.

[15] McDougall S, Hungr O. Dynamic modeling of entrainment in rapid landslide[J]. Canadian Geotechnical Journal, 2005,42:1437-1448.

[16] Pastor M. The “SafeLand” Project: Living with landslide risk in Europe, Landslide runout: Guidelines for using a simple propagation code[R]. Caminos, Fundación Agustín de Betancourt ETS de Ingenieros de Caminos, 2012.

Numerical Analysis on Landslides Based on A SPH Depth Integral Model

TAO Yanqi1, LI Jiagang2

(1.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian,Liaoning116024,China;2.GeneralResearchInstituteofChinaNationalOffshoreOilCorporation,Beijing100081,China)

Landslides can cause serious damages to the structure of the engineering, sliding velocity and distance are two important parameters in the quantification and analysis of landslides. However, the existing prediction method of sliding velocity and distance is complicated. In view of this situation, a governing equation was established considering soil consolidation and erosion effect. The SPH depth integral method was used to simulate landslides by the selected frictional rheological model. Comparing the time history curve of velocity, length of sliding body under the different conditions of slope angle, contact frictional coefficient and erosion rate, the final deposit shapes of the sliding body were analyzed, the maximum sliding distance and velocity were summarized and the underlying influence of related physical parameters were discussed. These research results can provide some technical reference for the disaster warning of landslides.

sliding velocity; SPH depth integral model; frictional rheological model; erosion effect

10.3969/j.issn.1672-1144.2015.05.022

2015-05-03

2015-06-01

国家自然科学基金(50909014)；国家重大科技专项“南海深水油气开发示范工程”子课题“南海北部陆坡区地质灾害风险评价预测研究”(2011ZX05056-001-02)；中央高校基本科研业务费专项资金资助

陶言祺(1989—)，男，安徽蚌埠人，硕士，主要从事水利规划和水工设计工作。E-mail:1056047556@qq.com

李家钢(1964—)，男，辽宁大连人，工程师，硕士，主要从事海洋地质灾害防治研究。E-mail:lijg2@cnooc.com.cn

P642

A

1672—1144(2015)05—0112—05