横掠周期性密集管束流动换热的数值模拟

余徐飞,　王治云,　李起耘,　黄文和,　陆廷安,　杨　茉

(1.上海理工大学 能源与动力工程学院,上海　200093; 2.上海市浦东新区特种设备监督检验所,上海　200136;

3.上海市特种设备监督检验技术研究院,上海　200333)



横掠周期性密集管束流动换热的数值模拟

余徐飞1,王治云1,李起耘2,黄文和3,陆廷安2,杨茉1

(1.上海理工大学 能源与动力工程学院,上海200093; 2.上海市浦东新区特种设备监督检验所,上海200136;

3.上海市特种设备监督检验技术研究院,上海200333)

摘要：在较宽的雷诺数范围内,使用CFD软件、SIMPLE算法和QUICK格式,对流体横掠不同管间距的顺排密集型管束,在周期性充分发展段的流动换热进行了数值模拟.选用几何间距与经验公式中相同的管束模型进行计算,将数值结果与前人已存在的经验公式和实验结果进行比较,确保数值模拟方法的正确性.通过分析3种不同计算模型的流场、换热系数等,验证了针对高度密集管束采用周期性边界条件和对称性边界条件的合理性.将其与大间距顺排管束的流动换热特性进行对比,结果表明,密集管束换热系数最高可达大间距管束换热系数的3倍,可为工业上换热器管排布置方式提供参考.

关键词：横掠管束; 密集型; 周期性; 数值模拟

横掠管束的对流换热在工业上有广泛应用,如电站锅炉省煤器、空气预热器、过热器等的烟气侧传热,都是这种横掠管束对流换热.这种换热的一个比较显著的特点是,在流动方向上,换热通道的几何结构是周期性变化的.当管排足够多时,这种流动换热呈现为所谓的周期性充分发展换热[1-2],即在流动方向上流动和换热随几何周期发生周期性变化.对于此类外掠周期排列物体的流动换热问题,越来越多的研究者采用数值模拟的方法进行研究.Nobile等[3]通过数值模拟对周期性波纹板通道的形状等几何参数进行优化;Korichi等[4]对上下壁面均周期性地安装有障碍物的矩形通道内的强化换热进行了数值分析.本文关注应用数值模拟方法研究横掠光管管束在周期性充分发展段的流动换热.早期茹卡乌斯卡斯[5]对这类光管管束换热进行了实验研究;Paul等[6]对大间距横掠管束湍流流动进行了实验验证和数值分析;杨茉等[7]采用周期性充分发展的概念对横掠管束的流动进行了数值模拟和烟可视化实验;潘维等[8]采用标准k-ε模型对气体横掠顺排和错排管束的流场进行了数值模拟;Khan等[9]通过公式推导和数学分析的方法得到横掠顺排和叉排管束的流动换热规律,管束的平均换热系数取决于管束横向纵向间距以及雷诺数Re和普朗特数Pr.

尽管对于横掠管束对流换热的研究已有数值模拟结果发表,但模拟技术还存在一些问题,特别是在取不同管间距的时候.对于流动方向上如何取周期性边界条件,文献资料给出的研究成果基本是肯定的.但垂直于流动方向上的上下两个边界条件如何给出,却缺乏确定的研究成果.由于管束中流动会出现交替脱落的、非对称的卡门涡,导致振荡和分岔等各种非线性现象[10-12],数值模型的上下两个边界处的流场和温度场是否对称还取决于管间距大小,所以模型的上下边界处在数值模拟的间距范围内能否定义为对称边界条件,需进一步探讨.此外,各种文献资料虽然一致认为管间距的变化对流动和换热影响较大,但不同文献所给出的定量结果却很分散,差别较大.文献[5]给出的实验结果没有体现管间距的变化,而Grimson[13]的实验结果与Zhang 等[14]的实验结果相比也存在一定的差异.另外,管间距变化时数值模拟结果的可靠性也需要进一步验证.

本文针对密集顺排排列的管束间的流动和传热问题进行数值模拟,探讨在流动方向引入周期性边界条件后横向边界条件的提法,并将数值模拟结果与实验结果比较,最后给出密集管束不同管间距时流动和换热的数值结果.

1计算模型和数学描述

1.1物理模型

图1为空气横掠二维正方形排列的顺排管束,即横向间距和纵向间距相等,间距取值为圆管直径D的1.04,1.08,1.12倍.拟计算的区域即为图1(b)中阴影区.

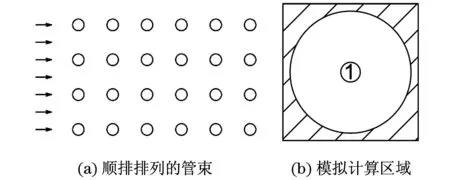
图1　密集顺排管束的排列方式示意图

1.2数学描述

采用标准k-ε两方程的湍流、非稳态模型来求解湍流对流换热问题,同时采用增强壁面函数法来处理壁面附近区域的粘性底层流动问题.对模型中每根圆管管尾部y+均进行考核,结果都满足增强壁面函数法的要求.对于低雷诺数时标准k-ε湍流模型是否适用的问题,选用层流模型和标准k-ε湍流模型分别进行模拟,并将计算结果与格里姆森实验结果进行比较,确定低雷诺数时可选用湍流模型来进行数值模拟.采用SIMPLE算法[15]进行问题的求解,动量和能量方程的离散选用具有三阶精度的QUICK格式.

此二维强制对流换热问题的计算基于以下假定:

a. 流体不可压缩,忽略温度对物性的影响,假设各项物性为常数;

b. 流动与换热均处于周期性充分发展阶段;

c. 壁面处流体无滑移;

d. 忽略体积力和粘性耗散无内热源.

描述不可压缩流体流动与换热的k-ε模型控制方程为

连续性方程

(1)

动量方程

(2)

k方程

(3)

ε方程

(4)

能量方程

(5)

其中

(6)

式中：x为坐标；u为速度分量；i，j为张量指标；t为时间；k为湍流脉动动能；ε为脉动动能耗散率；T为温度；ρ为流体密度；μ为动力粘度；cp为定压比热容；μt为湍流粘度；σt为能量普朗特数，取值0.85；σk为脉动动能普朗特数，取值1.0；σε为脉动动能耗散率普朗特数，取值1.3；模型系数cμ,c1和c2分别取值0.09，1.44和1.92.

无量纲温度

式中:T为流体温度;TW为壁面温度;Tb(X)是横坐标为X的截面上流体平均温度,代表了截面的平均能量.

模型满足的边界条件如下:

x方向,进出口周期性边界条件为

式中:D为圆管直径;S1为沿流向方向前后两根管圆心的距离;S2为垂直流向方向上下两根管圆心的距离.

y方向,上下界面对称边界条件为

圆周上采用无滑移固定壁面条件:uwall=vwall=0,T=TW.式中,uwall,vwall分别为壁面流体在x,y方向的分速度.

2计算结果和分析

2.1对称边界条件的验证

由于在管束间流动会形成交替脱落的卡门涡,严格说图1(b)计算区域上下边界的物理条件不是对称的,但考虑讨论的是密集管束,管间距很小,卡门涡的形成受到了抑制,因此,笔者认为对这种特殊情况采用对称边界条件不会引起太大的误差.

为了验证采用上下对称性边界条件的合理性,对单根管模型、竖排5根管、横排5根管这3种模型(如图2所示)分别进行数值模拟并加以比较.3种模型中用来比较验证的换热管分别标示为换热管①,②,③.

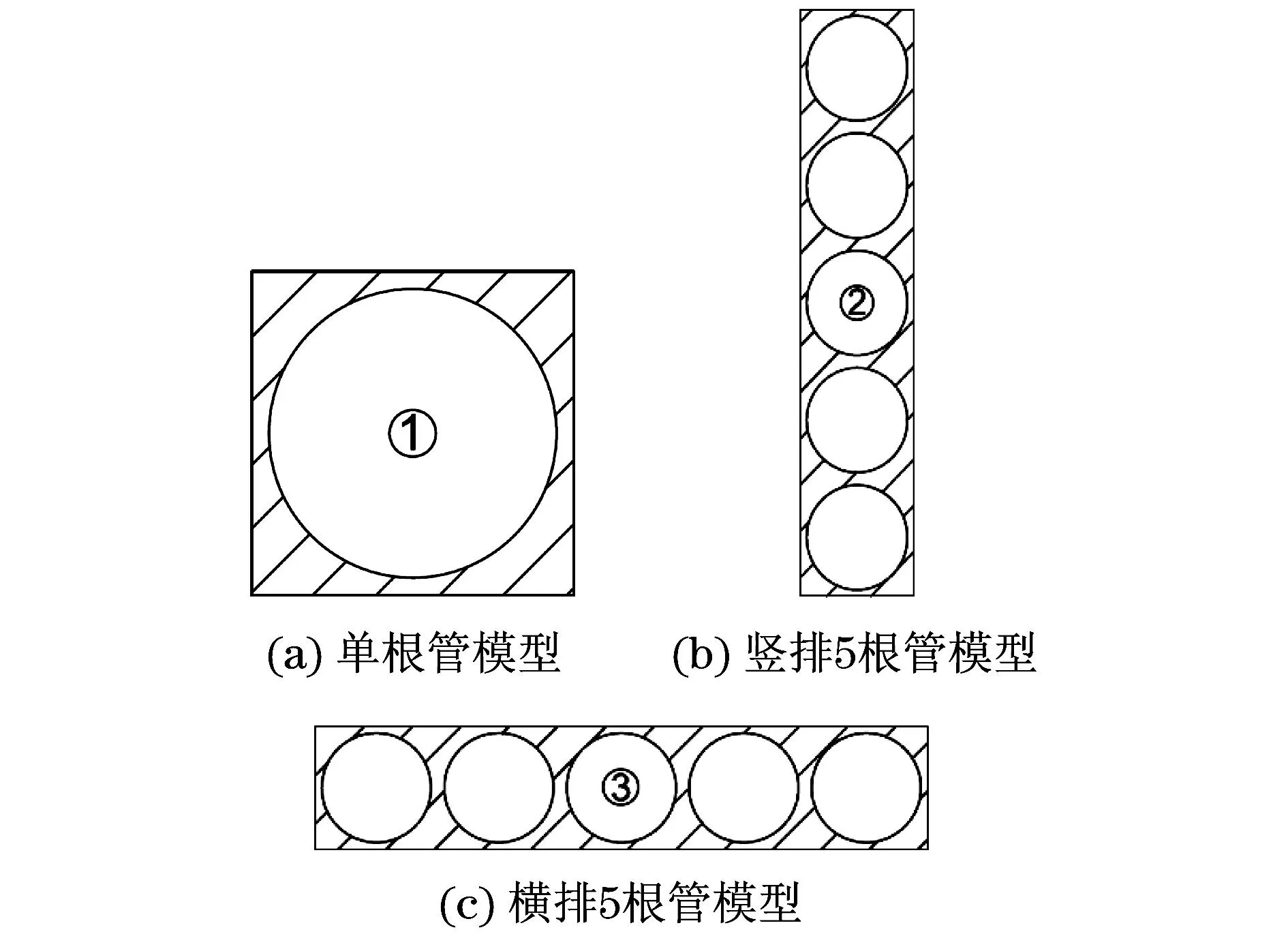
图2　不同模型的排列方式示意图

以布置尺寸为S1/D=S2/D=1.12的正方形管束为例,在Re=5 000,30 000的工况下对这3种模型的模拟结果进行比较.通过对比3种模型的流场和温度场的等值线图发现,在Re=5 000,30 000时,换热管①,②,③周围的流场与温度场无明显差异.图3定量给出了3种模型中采用周期性边界条件和对称性边界条件时换热管①,②,③所得出的平均努塞尔数Nuavg,可以看出3种模型的差别极小,最大偏差不超过4%,最小达到0.3%.

图3　3种模型中换热管①,②,③的对比图

从以上分析可知,采用上下对称性边界条件来简化计算模型是合理的.以下的计算模型均采用简化后的模型,因为它可以在保证一定精度的前提下,大大地减少计算时间.

2.2模拟结果与公式对比验证

目前已有的关于流体横掠管束的换热公式有很多,其中传热学书中普遍采用的是文献[12]的实验结果和文献[5]的经验公式.

由于Grimson的实验关联式:Nu=BRem,其适用范围为Ref=2 000~40 000,系数B,m在Grimson的论文中有详细说明.故验证的雷诺数在此范围内取值为2 000,3 500,5 000,7 500,15 000,22 500,30 000,37 500,40 000,在此雷诺数范围内茹卡乌斯卡斯的实验回归公式为

式中:Ref,Prf按流体的温度确定;Prw按管束的平均壁温确定.

为了与Grimson的实验关联式相对比,选取的大间距参数与其实验时参数一致:横向间距S2/D恒为3,纵向间距S1/D分别为2和3.将数值计算得到的流体与圆管换热的平均Nu数与实验结果和经验公式同时进行了对比验证,确定数值模拟的正确性.

通过对4种不同间距时平均努赛尔数的模拟值与两种不同经验公式的模拟值对比发现,数值模拟结果与两个经验公式之间存在较大的误差,最大误差接近30%,并且数值模拟结果更接近Grimson的经验公式.

分析其中原因,笔者认为,首先Grimson的经验公式中并没有考虑物性对换热系数的影响,而且Grimson本人以及Hausen[16]均在最初关联式的基础上提出过不同的修正,故存在一定误差是可以接受的.其次,茹卡乌斯卡斯经验公式并未包含间距对Nu的影响,其仅适用于排列间距S2/S1<2的管束,因为此经验公式在计算排列紧凑的管束换热时采用的是入口处流速而不是流动截面最小处的最大流速.Khan等[9]在分析结果中便提到这一点,他得到的分析结果与Grimson吻合较好而与茹卡乌斯卡斯相差较大.

Zhang等[14]在横掠管束的实验中也发现:对于单管的实验结果能与茹卡乌斯卡斯经验公式吻合良好,误差小于5%;而针对管束的实验结果则与Grimson和茹卡乌斯卡斯关联式相差很大,例如S2/D,S1/D分别为3和1.25时,实验模拟结果与两种关联式的误差均超过40%.文献[14]给出了S2/D,S1/D分别为3和1.1时的模拟结果,选择与之相同的模型进行了数值模拟并给出结果对比.

图4为数值模拟结果与Zhang等的实验结果和茹卡乌斯卡斯关联式的对比.与其他间距下的对比结果相同,此间距下的数值模拟结果与茹卡乌斯卡斯的结果相差很大,但与文献[14]的实验结果吻合良好,由此也证明本文的数值模拟结果是可靠的.

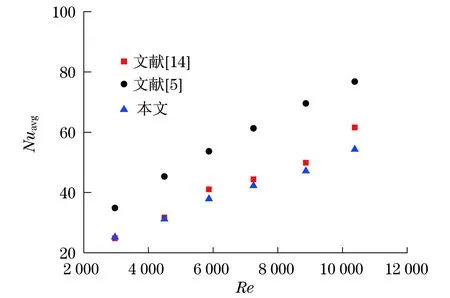
图4　模拟值与文献[5]及文献[14]的对比图

2.3间距对流动换热的影响

从流动和换热的两个角度对密集型管束与大间距管束进行对比.图5为Re在2 000~40 000范围时,7种不同排列方式(S1/D×S2/D=3×3,2×3,1.5×3,1.25×3,1.12×1.12,1.08×1.08,1.04×1.04)的管束流动换热时的阻力系数f和Nuavg随Re的变化曲线.

由图5可以看出,不同间距的Nu和f随Re的变化趋势一致,Nu均随着Re的增加而增大,而f则随Re的增加而降低,但下降趋势随着Re的增加而降低.当Re=2 000时,Nuavg随间距增大而减小且趋于平缓,间距增大到1.25×3以后,Nuavg随间距和Re改变而发生的变化很小,即间距和Re对Nuavg的影响不大;但当Re=40 000时,情况发生了变化,在密集型排列方式中,Nuavg随着间距减小而增大,1.04×1.04的排列方式最优.

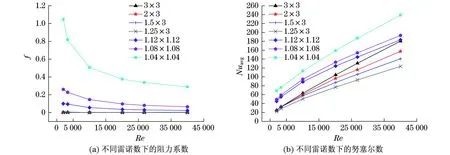
图5　不同间距管束在不同雷诺数下的参数对比图

在所选取的Re范围内,3种密集型排列的Nuavg基本均在大间距排列的Nuavg之上.当Re=2 000和40 000时,最大努塞尔数和最大阻力系数都出现在间距为1.04×1.04的管束上,最小努塞尔数和最小阻力系数都出现在间距为1.25×3的管束上.当Re=2 000时,最大努赛尔数是最小努塞尔数的3倍左右;当Re=40 000时,最大努塞尔数是最小努塞尔数的2倍左右.

3结论

管束的排列方式对管束绕流流动换热有很大影响,为了系统地认识管束流动换热随间距的变化情况,在Re=2 000~40 000的范围内对不同排列间距下的管束进行了数值模拟研究,得出的结论如下:

a. 对于绕流稀疏排列和密集排列的顺排管束对流换热,采用前后周期性边界条件和上下对称性边界条件获得的数值结果是可靠的.

b. 雷诺数较大(Re=40 000)时,密集管束与大间距管束的换热规律不同.在密集型排列方式中Nuavg随着间距减小而增大,顺排1.04×1.04的排列方式最优,而在大间距的排列方式中Nuavg随着纵向间距增大而增大,顺排3×3的排列方式传热性能最优.

c. 密集型的排列方式有助于强化流体绕流管束的换热效果.密集管束换热系数最高可达大间距管束换热系数的3倍.

参考文献：

[1]陶文铨.数值传热学[M].西安:西安交通大学出版社,2001.

[2]Patankar S V,Liu C H,Sparrow E M.Fully developed flow and heat transfer in ducts having streamwise-periodic variations of cross-sectional area[J].ASME Journal of Heat Transfer,1977,99(2):180-186.

[3]Nobile E,Pinto F,Rizzetto G.Geometric parameterization and multiobjective shape optimization of convective periodic channels[J].Numerical Heat Transfer,Part B:Fundamentals:An International Journal of Computation and Methodology,2006,50(5):425-453.

[4]Korichi A,Oufer L.Heat transfer enhancement in oscillatory flow in channel with periodically upper and lower walls mounted obstacles[J].International Journal of Heat and Fluid Flow,2007,28(5):1003-1012.

[5]茹卡乌斯卡斯.换热器内的对流传热[M].北京:科学出版社,1986.

[6]Paul S S,Rmiston S J,Tachie M F.Experimental and numerical investigation of turbulent cross-flow in a staggered tube bundle[J].International Journal of Heat and Fluid Flow,2008,29(2):387-414.

[7]杨茉,叶建军,邹宽,等.横掠管束非稳态周期性充分发展流动的数值模拟[J].西安交通大学学报,2001,35(11):1122-1125.

[8]潘维,池作和,斯东波,等.匀速流体横掠管束的流场数值模拟[J].浙江大学学报:工学版,2004,38(8):1043-1046.

[9]Khan W A,Culham J R,Yovanovich M M.Convection heat transfer from tube banks in crossflow:analytical approach[J].International Journal of Heat and Mass Transfer,2006,49(25/26):4831-4838.

[10]杨茉,黄夫泉,章立新,等.水平板自然对流换热的非线性特性[J].工程热物理学报,2008,29(2):275-277.

[11]王治云.开口腔内耦合换热的模拟及其解的非线性分析[D].上海:上海理工大学,2011.

[12]张昆.圆筒内开缝圆筒自然对流及非线性特性[D].上海:上海理工大学,2011.

[13]Grimson E D.Correlation and utilization of new data on flow resistance and heat transfer for cross flow of gases over tube banks[J].Transactions of the ASME,1937,59:583-594.

[14]Zhang Y W,Chen Z Q.The effect of a gap between layers on the heat transfer performance of aligned tube banks[J].Heat Transfer Engineering,1992,13(2):33-41.

[15]申春赟,杨茉,王津,等.圆内开缝圆不同开缝方向自然对流换热[J].上海理工大学学报,2013,35(5):425-429.

[16]Hausen H.Heat transfer in counterflow,parallel flow,and cross-flow[M].New York:McGraw-Hill Inc,1983.

(编辑:丁红艺)

第一作者： 闫士举(1977-),男,副教授.研究方向:微创医疗器械.E-mail:yanshjqq@aliyun.com

第一作者： 裘俊(1981-),男,工程师.研究方向:流体机械、风机检测.E-mail:36119688@qq.com

Numerical Simulation of Periodically Fully Developed Flow and Heat Transfer in Crossflow over Intensive Tube BanksYU Xufei1,WANG Zhiyun1,LI Qiyun2,HUANG Wenhe3,LU Tingan2,YANG Mo1

(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;

2.Shanghai Pudong Institute of Special Equipment Inspection,Shanghai 200136,China;

3.Shanghai Institute of Special Equipment Inspection and Technical Research,Shanghai 200333,China)

Abstract：To investigate the effect of the longitudinal pitch and the transverse pitch on the convective heat transfer in the crossflow over intensive in-line tube banks,an analytical study using the CFD (computational fluid dynamics) code and the SIMPLE (semi-implicit method for pressure-linked equations) algorithm with the QUICK (quadratic upwind interpolation of convective kinematics)scheme was performed.A bundle model with the same longitudinal reduction and transverse pitch as those in the empirical formula was selected in the simulation.By comparison of numerical results with existing empirical formulas and experimental results,the correctness of the numerical simulation method was ensured.Three kinds of bundle models were simulated.By analyzing the results of the flow field and the heat transfer coefficient of tube banks,it indicates that the periodic boundary conditions and the symmetryical boundary conditions given in the model are reasonable.By comparing the flow and heat transfer coefficient characteristics of the intensive and sparse array tube banks,the results show that the heat transfer coefficient of intensive tube bundles is up to three times as big as that of sparse tube banks.The conclusion can provide a reference to the arrangement of industrial heat exchanger tubes.

Key words：tube banks; intensive; periodical; numerical simulation

基金项目：浙江省科学技术厅科技条件建设项目(2013F0074)

收稿日期：2014-09-13 2014-10-20

DOI：10.13255/j.cnki.jusst.2015.06.013 10.13255/j.cnki.jusst.2015.06.011

文章编号：1007-6735(2015)06-0577-06 1007-6735(2015)06-0568-05

中图分类号：TK 124

文献标志码：A