速度管排水采气井筒压降模型的评价及优选

田云，王志彬，李颖川，白慧芳，李克智

（1.西南石油大学石油与天然气工程学院，四川 成都 610500；2.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610500；3.中国石化华北分公司工程技术研究院，河南 郑州 450006）

速度管排水采气井筒压降模型的评价及优选

田云1，王志彬2，李颖川2，白慧芳1，李克智3

（1.西南石油大学石油与天然气工程学院，四川 成都 610500；2.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610500；3.中国石化华北分公司工程技术研究院，河南 郑州 450006）

准确计算速度管中气液两相流压力降，是速度管排水采气工艺优化设计、生产动态及排液效果分析的基础。文中以Orville Gaither 1963年以天然气/水作为实验流动介质，在管径25.4，31.75 mm速度管中测试的单相液流、气液两相流的实验数据为基础，首先优选了摩阻系数计算方法，其次对速度管中气液两相流的压降模型进行评价和优选，最后利用大牛地3口水平井速度管流压测试数据进行了验证。利用单相液流测压数据进行摩阻系数优选表明，AGA方法计算结果与实际情况最吻合，误差最小（压降平均绝对误差为22.37%）；8个常用气液两相管流压降模型评价表明，Gray模型准确性最好，其次为Ansari模型。这为速度管排水采气井优选出了可靠的两相流压降计算模型，有助于提高工艺设计及排液效果诊断水平。

速度管；排水采气；井筒；压降；评价与优选

对于低压、低渗、低产及有水气藏，在生产中后期，部分井甚至在生产初期，气井产量就开始低于携液临界气流量［1］，井筒逐渐积液，严重影响气井的正常生产，部分气井甚至会出现积液停产现象。为此，需通过降压带液、泡排、气举、优选管柱（速度管）等排水采气工艺措施，来维持气井连续生产［2-3］。

速度管柱排水采气工艺技术能较好地解决积液气井存在的问题，目前，其研究主要是依据连续携液理论进行速度管柱尺寸的选择及工艺效果评价,而对速度管内的压降和摩阻分布研究涉及较少。笔者利用Orville Gaither［4］1963年公开发表的实验数据和大牛地3口典型井的测试数据，对速度管井筒压降模型进行了优选和评价，这为速度管排水采气井工艺优化设计和速度管排液效果分析提供了必要的理论依据。

1 速度管排水采气工艺概述

速度管排水采气工艺，是将优选的较小管径油管（即速度管）作为生产管柱，安装于井筒，进而降低井筒临界携液流速，增大井筒中气体的流速，减少气液的滑脱损失，提高气井带液能力，以达到排除井底积液、维持气井平稳生产的目的［5］。速度管排水采气技术，工艺可靠，可不压井作业，减轻了对地层的伤害；一次性投入低，依靠气井自身能量排水，节省了人力、物力。该工艺技术在四川、大牛地、长庆等气田得到了广泛的试验和应用，取得了较好的排水采气效果，为改善低产低效井的开发效果提供了新的技术手段。随着油气田的不断开发，低产气井逐年增多，该技术应用前景广阔［6-7］。

速度管排水采气工艺设计的理论基础主要是连续携液理论［8］，以及速度管气液两相管流压降计算模型。对于产气量较高、气液比较高、井筒流型为环状流的气井，可对比不同管柱尺寸的连续携液气流量与气井产气量的关系，优化管柱尺寸及下深；但对于产气量较低、气液比较低、井筒流型为段塞流的气井，若安装速度管后仍不能连续携液，则可对比分析井筒的滑脱损失、摩擦压降及总压降，以确定合理的速度管尺寸：这就需要正确选取气液两相管流压降模型，以提高速度管设计的准确性和可靠性。同时，速度管气液两相压降计算模型，也是速度管排水采气井动态分析、井筒积液量计算及排液效果诊断的理论基础［9-10］。

2 摩阻系数计算方法优选

速度管内气液混合物流速较高，摩阻压降较大。准确计算摩阻压降是计算速度管总压降的重要方面［11］，而摩阻系数是计算摩阻压降的重要参数，其计算的准确性直接决定了摩阻压降计算的准确性；因此，有必要对多相管流的摩阻系数进行分析。

研究表明，气液两相管流摩阻压降可采用单相气流或单相液流的摩阻系数进行近似计算［12］。Weymouth 1912年从生产实践中归纳出计算井筒摩阻压降的纯经验公式。Moody 1944年发表了各种自然粗糙管道的摩阻系数图版，被公认为单相流体沿程摩阻系数的基准图版，被广泛应用［13］。Panhandle认为，摩阻系数λ是雷诺数Re的函数，理论上只适用于水力光滑区（这是由于美国的管子很光滑（取粗糙度k=0.020 mm））。之后，Panhandle提出了可用于雷诺数较大的阻力平方区，即 Panhandle B式。美国燃气协会（American Gas Association，简称AGA）认为：在紊流流速较低（不完全紊流）时，摩阻系数λ只与雷诺数Re有关；在紊流流速较高（完全紊流）时，摩阻系数只是相对粗糙度的函数。

1963年Orville Gaither利用天然气作为流动介质，对单相气体在速度管中的流动规律进行了研究。实验测试的数据如下：气流量1.37×104～5.31×104m3/d；天然气相对密度0.62；平均温度15～23℃；油管尺寸25.40，31.75 mm；井口压力0.59～4.54 MPa；井底压力1.52～5.55 MPa；压降0.29～4.30 MPa；实验组数为25（管径25.40 mm）+27（管径31.75 mm）。

粗糙度取0.032 mm，利用Moody，Panhandle A，Panhandle B，AGA，Weymouth摩阻系数计算方法计算了单相气体在油管和环空中的流动压力降，并与测试值进行了对比（见图1）。

图1 不同方法下的压降计算值与单相气流测试压降对比

不同摩阻系数计算方法计算的井筒压降与测试压降的误差统计如表1所示。从表1可知，利用AGA方法计算的压降误差相对较小。

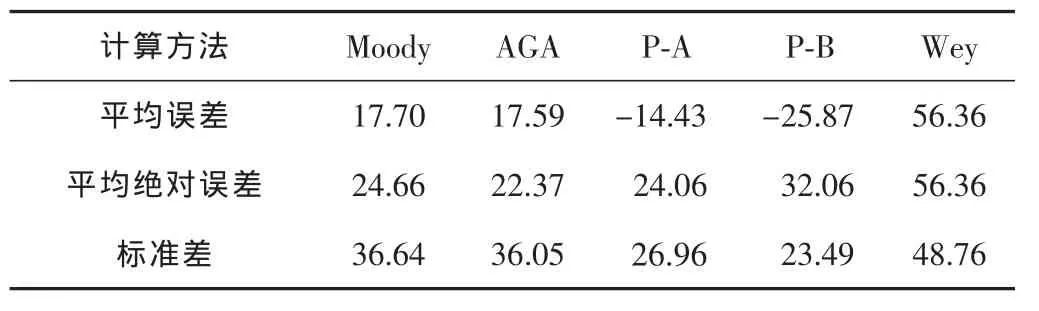
表1 单相气体压降计算误差统计 %

3 两相流井筒压降计算

Orville Gaither1963年利用天然气和地层水作为流动介质，对气液两相流体在速度管中的流动规律进行了研究。

实验测试的数据参数范围如表2所示。

表2 气液两相流动实验参数范围

利用文献中的实验数据，将粗糙度取为0.032 mm，选取AGA方法计算摩阻系数，各两相管流模型计算的压降与测试值对比如图2所示。

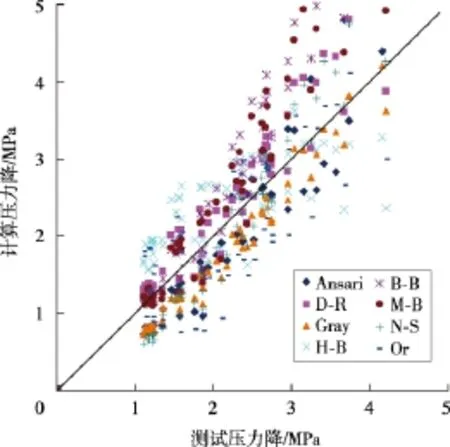
图2 两相管流模型计算压力降与测试值对比

表3为各模型预测压降与实测压降对比得到的压降平均误差、压降平均绝对误差和压降标准差。其中：压降平均误差表示模型的整体偏差，平均绝对误差表示平均误差的大小，标准差表示模型计算结果的离散程度［14-15］。从表3可知，Gray模型的各项误差最小，在各模型中性能最佳；从平均相对误差和标准差可知，Gray模型的对中性和离散程度均最好。计算压降平均误差相对较小的两相管流模型依次是 Gray模型、Ansari模型、No-Slip模型。

表3 油管内流动压降误差统计 %

4 实例分析与验证

以大牛地几口典型的水平井为例。在3口水平井安装速度管后进行了流压测试，其基础数据见表4。

表4 水平井速度管流压测试基础数据

将压力计下放点置于造斜点附近，完成水平井垂直段的流压测试。利用流压测试数据对两相管流模型再次进行了评价，测试压降与计算值对比见表5。

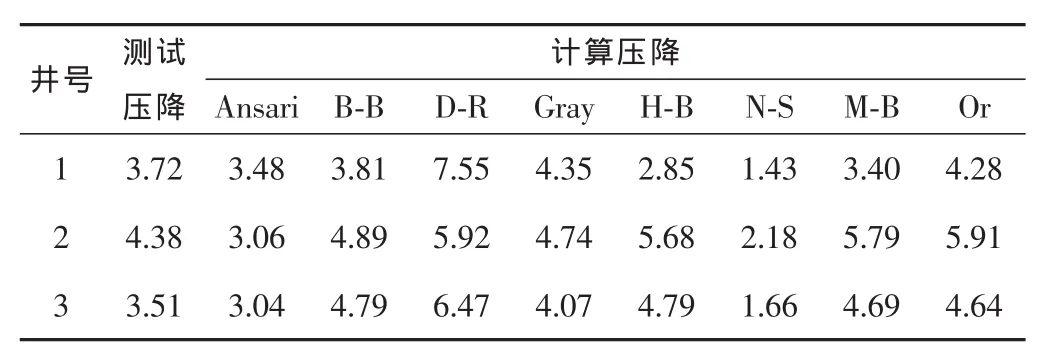
表5 水平井速度管测试压降与模型计算压降对比 MPa

压降误差统计见表6。

表6 水平井速度管流动压降误差统计 %

本文主要以压降平均绝对误差为依据，并参考其他误差，比较各压降模型的准确性。

从表5和表6可知：Gray模型压降平均绝对误差为13.70%，标准差为4.80%，是参与比较的模型中最佳的；其次为Hagedorn-Brown模型和Ansari模型。而常规管柱气水两相流压降模型的评价结果表明，Hagedorn-Brown模型计算的误差最小。这是由于该模型是唯一根据现场试验井数据推导而来，对于产水气井条件，它明显优于其他基于实验数据的经验方法［16］。

由此可见，速度管两相流压降模型评价结果与常规管柱模型评价结果存在一定的差异。出现这种差异的原因在于：在相同流量的情况下，速度管中气液混合物流速比常规尺寸管柱流速高，流型也有一定的差异，井筒的滑脱损失程度有一定差异；加之小管径流动时的实验数据量相对较少，以上几种经验模型是基于大管柱气液两相流动的实验数据建立起来的，未充分考虑管径的影响，因而导致对速度管气液两相流压降计算不准，误差较大。

为此，综合考虑Orville Gaither的实验数据和大牛地速度管的流压测试数据，以及各气液两相管流模型的评价结果，应首选Gray模型对大牛地气田速度管井筒压力分布进行计算，其次选用Ansari模型。

5 结论

1）速度管中气液混合物流速较高，摩阻压降较大，准确选取摩阻系数计算方法是进行速度管压降计算的基础。利用单相液流测压数据进行摩阻系数优选表明，AGA方法计算结果与实际情况最吻合，误差最小。

2）根据1963年Orville Gaither的实验数据和大牛地速度管的流压测试数据，对8个常用气液两相管流压降模型评价。结果表明，速度管排水采气时，宜首选Gray模型，其次为Ansari模型进行流压计算。

［1］周瑞立，周舰，罗懿，等.低渗产水气藏携液模型研究与应用［J］.岩性油气藏，2013，25（4）：123-128.

［2］田相雷，蒋海岩，岳艳如，等.气举排水采气生产规律研究［J］.断块油气田，2013，19（6）：760-763.

［3］白晓弘，田伟，田树宝，等.低产积液气井气举排水井筒流动参数优化［J］.断块油气田，2014，21（1）：125-128.

［4］Gaither O D，Winkler H W，Kirkpatrick C V.Single-and two-phase fluid flow in small vertical conduits including annular configurations［J］.Journal of Petroleum Technology，1963，15（3）：309-320.

［5］周舰，罗懿，刘岳龙，等.大牛地水平井速度管排液工艺研究与应用［J］.石油机械，2013，41（12）：102-105.

［6］赵彬彬，白晓弘，陈德见，等.速度管柱排水采气效果评价及应用新领域［J］.石油机械，2012，40（11）：62-65.

［7］林英松，蒋金宝，刘兆年，等.连续油管压裂新技术［J］.断块油气田，2008，15（2）：118-121.

［8］李闽，郭平，刘武，等.气井连续携液模型比较研究［J］.断块油气田，2002，24（6）：39-41，91.

［9］赵界，李颖川，刘通，等.大牛地地区致密气田气井积液判断新方法［J］.岩性油气藏，2013，25（1）：122-125.

［10］代志华.气井井筒积液诊断及排液效果分析［J］.化学工程与装备，2011，23（3）：85-87.

［11］李士伦.天然气工程［M］.北京：石油工业出版社，2008：109-117.

［12］喻西崇，冯叔初.多相管流中沿程摩阻系数分析［J］.油气田地面工程，2001，20（2）：3-4.

［13］Moody L F.Friction factors for pipe flow［J］.Trans.Asme，1944，66（8）：671-684.

［14］廖开贵，李颖川，杨志，等.产水气藏气液两相管流动态规律研究［J］.石油学报，2009，30（4）：607-612.

［15］刘通，任桂蓉，赵容怀.非环状流气井两相流机理研究［J］.岩性油气藏，2013，25（6）：103-106，132.

［16］李颖川，朱家富，秦勇.排水采气井油管和环空两相流压降优化模型［J］.石油学报，1999，20（2）：87-92.

（编辑 李宗华）

Evaluation and optimization of wellbore pressure drop model for drainage and gas recovery by velocity string

Tian Yun1,Wang Zhibin2,Li Yingchuan2,Bai Huifang1,Li Kezhi3
(1.School of Petroleum and Gas Engineering,Southwest Petroleum University,Chengdu 610500,China; 2.State key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu 610500, China;3.Research Institute of Engineering and Technology,Huabei Company,SINOPEC,Zhengzhou 450006,China)

Accurately calculating the pressure drop of two-phase flow in velocity string is the basis of optimizing design for drainage and gas recovery and analyzing production performance and drainage effect.In this paper,experiment data are from Orville Gather (1963)who carried out a single-phase and two-phase experiment in 25.4 and 31.75 mm velocity strings using natural gas/water as experimental medium.Firstly,the calculation method of friction factor is optimized.Secondly,the pressure drop of two-phase flow is evaluated and optimized.Finally,the optimum pressure drop of two-phase flow is verified by production data of three typical horizontal wells in Daniudi Gas Field after installing velocity string.Using the measured pressure data of pure liquid flow to optimize friction coefficient shows that the calculation of AGA method is the most consistent with actual results,whose error is the least（the average absolute error of pressure drop is 22.37%）.The evaluation of eight frequently-used two-phase flow pressure models shows that the priority selection to calculating wellbore pressure drop is Gray model and the second is Ansari model.This study can optimize a dependable calculation model of two-phase flow pressure drop for drainage and gas recovery by velocity strings and help to improve the technology design and the diagnosis level of drainage effect.

velocity string;drainage and gas recovery;wellbore;pressure drop;evaluation and optimization

国家科技重大专项课题“大牛地致密低渗气田特殊结构井渗流机理与采气工艺研究”（2011ZX05045-05-01）

TE375

：A

10.6056/dkyqt201501029

2014-09-15；改回日期：2014-11-21。

田云，女，1989年生，在读硕士研究生，研究方向为采油采气理论与工程技术。E-mai：swputy@163.com。

田云，王志彬，李颖川，等.速度管排水采气井筒压降模型的评价及优选［J］.断块油气田，2015，22（1）：130-133.

Tian Yun，Wang Zhibin，Li Yingchuan，et al.Evaluation and optimization of wellbore pressure drop model for drainage and gas recovery by velocity string［J］.Fault-Block Oil&Gas Field，2015，22（1）：130-133.