水平井偏心环空稳定顶替界面形状研究

冯福平，邓平，邢均，吕媛媛，张嵇南

（1.东北石油大学石油工程学院，黑龙江 大庆 163318；2.中国石油新疆油田公司工程技术研究院，新疆 克拉玛依 834000；3.中国石油大庆油田工程有限公司，黑龙江 大庆 163712；4.中国石油辽河油田公司勘探开发研究院，辽宁 盘锦 124010；5.中国石油吉林油田公司科技处，吉林 松原 138000）

水平井偏心环空稳定顶替界面形状研究

冯福平1，邓平2，邢均3，吕媛媛4，张嵇南5

（1.东北石油大学石油工程学院，黑龙江 大庆 163318；2.中国石油新疆油田公司工程技术研究院，新疆 克拉玛依 834000；3.中国石油大庆油田工程有限公司，黑龙江 大庆 163712；4.中国石油辽河油田公司勘探开发研究院，辽宁 盘锦 124010；5.中国石油吉林油田公司科技处，吉林 松原 138000）

固井顶替界面反映了顶替流体的掺混程度，降低顶替界面长度能够有效提高顶替效果和环空封固质量。由于水平井顶替剖面上密度差引起的驱动力与流体微元所在位置有关，即使稳定顶替的条件下，顶替界面也会由于驱动力的差异而产生局部凸进，使得顶替界面长度增加。文中考虑了水平井水泥浆与钻井液的密度差引起的驱动力沿周向角和半径的变化，采用二维Hele-Shaw顶替模型及微扰法理论，建立了水平井偏心环空稳定顶替界面形状描述模型，分析了水平井偏心环空顶替界面长度随密度差的变化规律，从而为设计合理的水泥浆与钻井液密度以降低水平井偏心环空稳定顶替界面长度提供理论依据。

水平井；套管偏心；稳定顶替；界面形状；密度差；顶替模型

0 引言

固井顶替界面反映了顶替流体的掺混程度，顶替界面越长，顶替液被污染的体积就越多，甚至存在顶替结束时顶替界面后缘未能返出封固段的可能性，造成钻井液窜槽，严重影响顶替效率和环空胶结质量。

固井顶替界面主要有稳定顶替、不稳定顶替和钻井液滞留窜槽3种形态［1-2］。国内外众多学者采用CFD数值模拟方法对顶替界面的稳定性及其形状进行了研究［3-7］，但由于计算过程中需要较多的网格数和较长的计算时间，且所模拟的结果都是在顶替开始的几秒时间内，并不能反映在实际细长井眼中顶替界面形态随时间的变化过程，同时该方法也无法描述环空钻井液的滞留现象。S.H.Bittleston等人［8-12］采用另外一种顶替界面的描述方法，主要基于二维Hele-Shaw模型，建立了稳定顶替时顶替界面的形状模型，但是该模型只考虑了周向角对顶替界面形状的影响。在水平井中，水泥浆与钻井液密度差所引起的驱动力取决于流体微元所在的位置。由于顶替剖面上驱动力的差异，顶替界面会产生局部凸进，增加了顶替界面长度（即环空周向上顶替液前缘与后缘之间的轴向距离）。

理论分析及室内试验均表明，无论是直井还是水平井，都可以通过选择合理的顶替流体性能获得稳定的顶替界面［13-14］。本文在实现稳定顶替界面的前提下，提出了修正的水平井偏心环空顶替界面形状描述模型，并以降低顶替界面长度为目标，分析了稳定顶替条件下水平井顶替界面长度随密度差的变化规律，从而为提高水平井偏心环空顶替效果及环空封固质量提供了理论依据。

1 水平井偏心环空Hele-Shaw顶替模型

1.1 水平井顶替流体密度差引起的驱动力

水泥浆驱替钻井液的动力包括驱替压差及密度差引起的驱动力。直井井眼截面为水平面，两相流体的密度差只产生轴向方向的驱动力，且井眼周向上各点相同。随着井斜角的增大，密度差引起的轴向驱动力逐渐减小，而周向驱动力逐渐增加。井斜角达到π/2时，密度差引起的轴向驱动力为0，而周向驱动力达到最大。井眼周向上各点受到的密度差引起的周向驱动力取决于流体微元到上井壁的铅垂高度，铅垂高度由流体微元体所在的周向角和半径决定，即水平井段钻井液微元体受到的密度差引起的驱动力是关于周向角和半径的函数。

在水平井段任取一横截面，以上井壁为基准点，如图1所示。由于井斜角为π/2，则A点钻井液微元体所受密度差引起的轴向驱动力为0，周向驱动力为

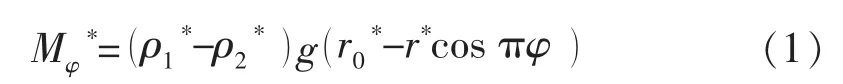
式中：Mφ*为钻井液微元体所受的密度差引起的周向驱动力，MPa；ρ1*为实际的水泥浆密度，g/cm3；ρ2*为实际钻井液密度，g/cm3；g为重力加速度，取值9.81 m/s2；为井眼实际半径，m；r*为环空中某一点到井眼中心的实际距离，m；πφ为周向角。

图1 水平井环空几何关系

由式（1）可以看出，水平井顶替界面上由密度差引起的周向驱动力与流体微元所在的位置有关。1）流体微元距井眼中心距离相同时，在0～π范围内，驱动力随周向角的增加而增大；在π～2π范围内，驱动力随周向角的增加而减小。2）周向角相同时，环空上侧驱动力随流体微元距井眼中心距离的增大而减小；环空下侧驱动力随流体微元距井眼中心距离的增大而增加（周向角π/2与3π/2处除外），即越靠近下井壁，密度差引起的周向驱动力越大，而在上井壁处周向驱动力最小。由于水平井顶替剖面上各点所受密度差引起的驱动力存在较大差异，即使在稳定顶替的条件下，密度差引起的驱动力差异也会使水平井顶替界面产生局部凸进，造成顶替界面分层流动，增加顶替界面长度和两相流体的掺混体积，影响水泥浆胶结质量。

1.2 水平井偏心环空Hele-Shaw顶替模型

Hele-Shaw模型描述的是在间距很小的2块无穷大平板之间流体的二维流动特性问题，其物理模型的特点为模型的长度远大于高度，且高度大于宽度。套管下入井眼后，环空水泥浆封固段的长度短则几百米，长则上千米，环空长度远大于环空周向长度，环空周向长度大于环空间隙宽度，因此Hele-Shaw模型非常适合处理油气井固井过程中的环空顶替问题。在环空中取出长度为2L的流体单元作为研究对象，设r0为无因次井眼半径，r1为无因次套管外径，Δr为无因次偏心距，e为偏心度，H为无因次环空间隙的一半，建立环空轴向和周向方向的无因次坐标系（ξ，φ），如图2所示。其中，ξ∈［-L，L］，φ∈［0，2］。初始顶替界面位置为ξ=0处，ξ∈［-L，0］单元体内充满水泥浆，ξ∈［0，L］单元体内充满钻井液。

假设条件如下：

1）水泥浆和钻井液均为赫-巴流体；

2）井眼规则，不考虑井径的变化；

3）忽略环空径向速度，只考虑轴向速度与周向速度的二维流动；

4）不考虑隔离液等中间流体，水泥浆与钻井液直接接触；

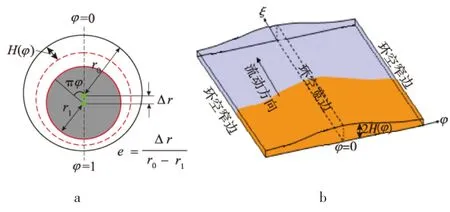
图2 Hele-Shaw顶替周向物理模型

5）顶替流体性能满足稳定顶替的条件，即顶替界面能达到稳定。稳定顶替时，顶替界面沿轴向均匀移动，考虑水平井顶替界面所受的驱替压差及密度差引起的驱动力特征［8-11］，结合N-S方程和赫-巴流体流变模式，可以得到顶替界面处流体的流动特性S为

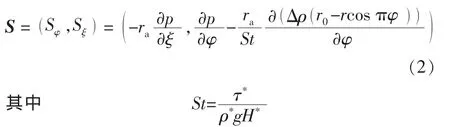
式中：ra为无因次环空半径；p为无因次驱动压力梯度；St为斯托克斯数；Δρ为无因次密度差；r为环空中某一点到井眼中心的无因次距离；τ*为水泥浆与钻井液所受到屈服应力的较大者，Pa；ρ*为水泥浆与钻井液密度的较大者，g/cm3；H*为环空间隙的一半，m。

柱坐标系下，顶替界面流体满足的连续性方程为

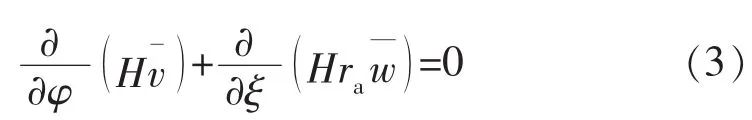
满足连续性方程的流函数为

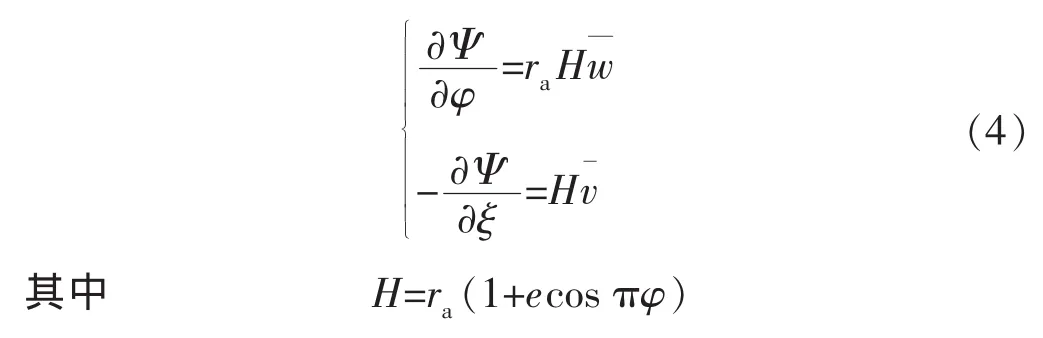
式中：χk为流体k的无因次驱动力与屈服应力之差，Pa，它为和H的函数，表示为；τk为流体k的无因次屈服应力；mk为流体k的无因次流性指数；κk为流体k的无因次稠度系数；下标k表示流体种类，1代表水泥浆，2代表钻井液；。

根据顶替界面上驱动力切向导数相等的条件，可以得到水平井顶替界面上顶替流体满足的条件为

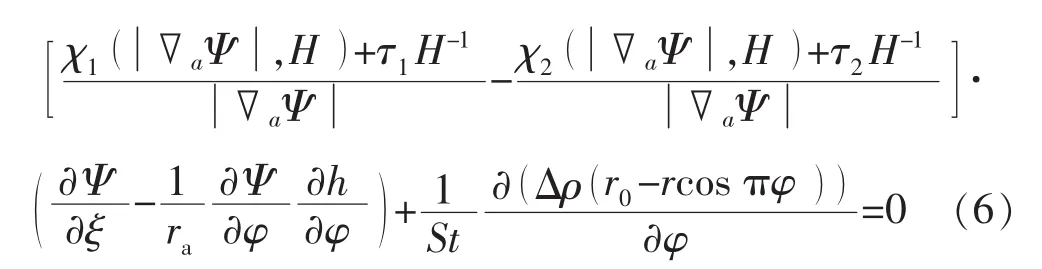
式中：h为任一时刻顶替界面上流体质点的位置。

2 套管居中时稳定顶替界面形状模型

2.1 顶替界面上流体质点的位置

水平井顶替过程中，顶替界面上由于密度差引起的驱动力越靠近环空低边越大，因此顶替界面局部凸进，同一时刻顶替界面上流体质点的运动位置各不相同。为了描述顶替界面上各质点的运动位置，设稳定顶替界面上任一质点的位置为ξ=h（φ，r），则h（φ，r）满足：

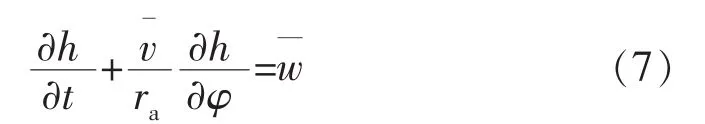
顶替界面上某一质点的运动位置由2部分组成：一是顶替界面整体向前移动的距离，t时间内质点位置的改变量为t；二是密度差引起的驱动力不同造成顶替界面沿轴向的形状变化，用g（φ，r）表示，当顶替界面达到稳定以后该值保持固定。因此，稳定顶替时顶替界面上流体质点的位置可以表示为

2.2 套管居中条件下稳定顶替界面形状模型

因为ra==1，式（4）对φ积分，同时忽略常数项，可得顶替界面处流函数的表达式：

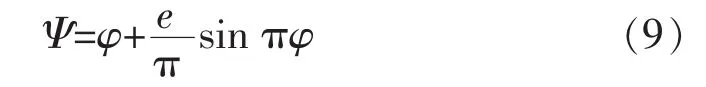
结合式（6）—（9），并整理可得：

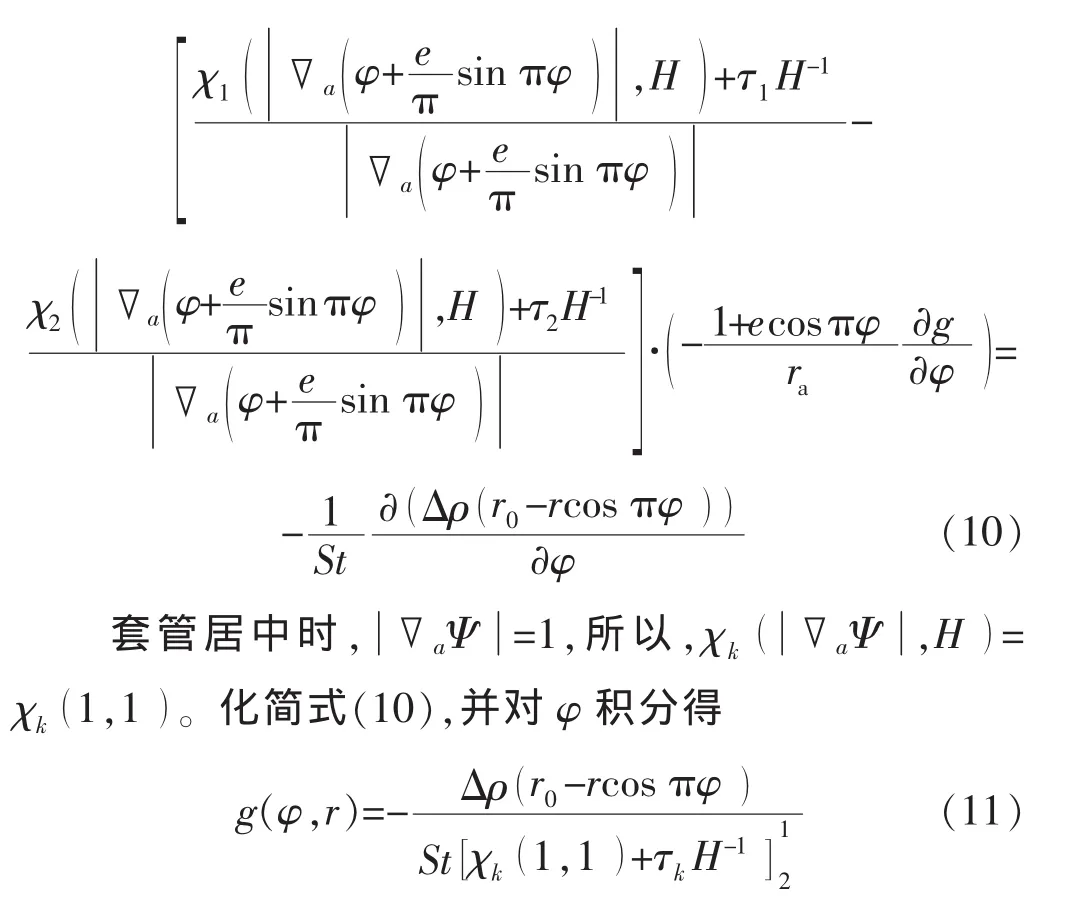
规定周向角πφ=π/2处为相对零点，可以得到套管居中时稳定顶替界面形状g（φ，r）的表达式：

3 偏心环空稳定顶替界面形状模型

为了得到套管偏心时稳定顶替界面的形状，引入微扰法理论，即把套管居中当作一种平衡态，给它一个微小的扰动，使其略微偏离原始状态，达到规定的套管偏心状态，通过求解微扰项可以得到套管偏心状态时的信息。

计算过程为：首先，分别将稳定顶替状态下的流函数Φk（φ，z）及顶替界面形状g（φ，r）这2个变量进行级数展开，分解成在某工作状态附近的小增量表达式；然后，略去高于一次的小增量项，获得近似的线性函数；最后，将近似的线性函数代入到流函数及顶替界面满足的约束条件中，通过分离变量方法进行积分，最终得到套管偏心条件下的稳定顶替界面形状模型。

套管居中时，稳定顶替界面形状计算公式（11）对周向角φ的偏导数为

将Φk（φ，z）及g（φ，r）这2个变量分别按偏心度e进行级数展开：

式（15）、式（16）忽略高于一次的小增量项，代入式（10）并进行线性化得

式中：χk′为

根据简单迭代法原理，整理式（17）并积分，规定周向角πφ=π/2处为相对零点，可以得到套管偏心条件下的稳定顶替界面形状为

式（18）中，第1项表示套管居中时的稳定顶替界面形状，第2项表示套管偏心对稳定顶替界面形状的影响。

4 偏心环空稳定顶替界面形状计算

以套管偏心度e=0.3为例，对不同密度差条件下的g（φ，r）进行计算，所用的基础数据如表1所示，计算结果如图3所示。

表1 稳定顶替界面形状计算基础数据

从计算结果可以看出：

1）环空中各点处的g（φ，r）值有较大不同，即使在周向角相同时，不同半径处的g（φ，r）值也不一样，说明顶替界面形状不仅与周向角有关，还与流体微元到井眼中心的距离有关，这一特性在之前的研究中并未得到体现。

2）由于定义环空中部周向角π/2处g（φ，r）值为相对零点，因此环空中各点g（φ，r）值有正有负。g（φ，r）值为正时，代表该点顶替界面位于环空中部顶替界面前方；g（φ，r）值为负时，代表该点顶替界面位于环空中部顶替界面后方。g（φ，r）的绝对值越大，说明该点顶替界面位置距离环空中部顶替界面位置越远。g（φ，r）的最大值为顶替界面前缘，g（φ，r）的最小值为顶替界面后缘，则无因次顶替界面长度为g（φ，r）max-g（φ，r）min。顶替界面长度越大，则水泥浆与钻井液接触体积越多，顶替流体的掺混现象越严重，稳定顶替的效果就越不好。

3）密度差较小时，密度差引起的驱动力不足以克服宽窄间隙产生的阻力效应，水泥浆沿宽间隙处产生凸进，g（φ，r）的最大值出现在环空高边的套管外壁处；密度差较大时，密度差引起的驱动力超过宽窄间隙产生的阻力效应，水泥浆沿窄间隙处产生凸进，g（φ，r）的最大值出现在环空低边的井壁处。水平井顶替界面凸进的位置及程度取决于套管偏心度与密度差的相对作用，两者对顶替界面凸进现象具有相互削弱作用。

4）偏心度为0.3时，随着密度差增大，环空顶替界面长度开始逐渐减小，密度差为0.5 g/cm3时顶替界面长度最小；其后，随着密度差的增大，顶替界面长度又逐渐增加。说明对于水平井偏心环空来说，存在最优的密度差使得顶替界面长度最短。通过设计合理的顶替流体密度差，可使顶替界面达到塞流顶替的平齐推进效果。

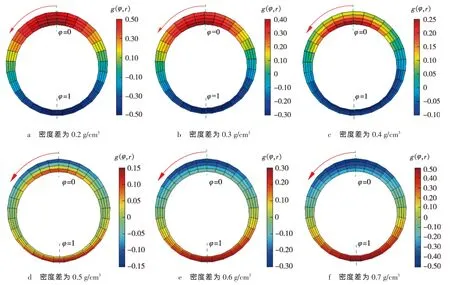
图3 不同密度差时环空g（φ，r）分布

采用该模型，对水平井套管偏心度为0.1～0.7时不同密度差条件下的顶替界面长度进行了计算，结果如图4所示。不同偏心度下无因次顶替界面长度最小时所对应的密度差，即为该偏心度下实现最好稳定顶替效果的最优密度差。

图4 不同偏心度条件下顶替界面长度随密度差的变化

水平井固井顶替时，可以根据现场扶正器下入数量及类型计算套管偏心度。在实现稳定顶替的前提下，进行水泥浆和钻井液密度的优化，从而降低顶替界面长度和顶替流体的掺混程度，提高固井顶替效果。

5 结论

1）水平井顶替剖面上流体微元所受密度差引起的驱动力取决于流体微元所在的位置，越靠近下井壁驱动力越大，在上井壁处驱动力最小。因此在密度差的作用下，即使在稳定顶替的条件下，水平井顶替界面也会产生局部凸进，造成顶替界面分层流动。

2）顶替界面形状g（φ，r）的绝对值越大，说明该点距离环空中部顶替界面的位置越远，水泥浆与钻井液的接触体积越大，在长封固段固井过程中会造成顶替流体掺混严重，甚至存在顶替结束时顶替界面后缘没有返出封固段的可能性。因此，即使在稳定顶替的条件下，也应降低顶替界面长度，从而提高顶替效果。

3）顶替流体密度差对水平井顶替界面的影响与套管偏心度相反。密度差较小时，水泥浆在环空高边的套管外壁处产生凸进；密度差较大时，水泥浆沿环空低边的井壁处产生凸进。水平井顶替界面的凸进位置及程度取决于套管偏心度与密度差的匹配关系，两者对顶替界面凸进现象具有相互削弱作用。

4）水平井套管偏心时，稳定顶替界面长度随着密度差的增加先减小后增大，存在最优的密度差使得顶替界面长度最短。因此在进行固井顶替时，应根据套管偏心情况，设计合理的水泥浆与钻井液密度差，降低顶替界面的局部凸进现象，使其达到塞流顶替的平齐推进效果。

［1］王瑞和，李明忠，王成文，等.油气井注水泥顶替机理研究进展［J］.天然气工业，2013，33（5）：69-76.

［2］冯福平，宋杰，艾池，等.固井顶替界面研究方法分析［J］.断块油气田，2014，21（4）：540-544.

［3］高永海，孙宝江，刘东清，等.环空水泥浆顶替界面稳定性数值模拟研究［J］.石油学报，2005，26（5）：119-122.

［4］杨建波，邓建民，冯予淇，等.低速注水泥时密度差对顶替效率影响规律的数值模拟研究［J］.石油钻探技术，2008，36（5）：62-65.

［5］Pks S，Yerubandi K B.Slim well completions：A 3D numerical approach for displacement to design effective cementing fluids［R］. SPE 132480，2010.

［6］Aranha P E，Miranda C R，Magalhães J V M，et al.Dynamic aspects governing cement-plug placement in deepwater wells［J］.SPE Drilling &Completion，2011，26（3）：341-351.

［7］张松杰，薛亮，汪志明，等.密度差对水平井固井顶替影响规律数值模拟研究［J］.钻采工艺，2012，35（6）：15-17.

［8］Bittleston S H，Ferguson J，Frigaard I A.Mud removal and cement placement during primary cementing of an oil well：Laminar non-Newtonian displacements in an eccentric annular Hele-Shaw cell［J］. Journal of Engineering Mathematics，2002，43（2/3/4）：229-253.

［9］Frigaard I A，Pelipenko S.Effective and ineffective strategies for mud removal and cement slurry design［R］.SPE 80999，2003.

［10］Pelipenko S，Frigaard I A.Visco-plastic fluid displacements in nearvertical narrow eccentric annuli：Prediction of travelling-wave solutions and interfacial instability［J］.Journal of Fluid Mechanics，2004，520：343-377.

［11］Pelipenko S，Frigaard I A.Mud removal and cement placement during primary cementing of an oil well（Part 2）：Steady-state displacements［J］.Journal of Engineering Mathematics，2004，48（1）：1-26.

［12］Pelipenko S，Frigaard I A.Two-dimensional computational simulation of eccentric annular cementing displacements［J］.IMA Journal of Applied Mathematics，2004，69（6）：557-583.

［13］Carrasco-Teja M，Frigaard I A，Seymour B.Cementing horizontal wells：Complete zonal isolation without casing rotation［R］.SPE 114955，2008.

［14］Malekmohammadi S，Carrasco-Teja M，Storey S，et al.An experimental study of laminar displacement flows in narrow vertical eccentric annuli［J］.Journal of Fluid Mechanics，2010，649：371-398.

（编辑 赵卫红）

Research on interface shape of steady-state displacement in eccentric annulus of horizontal well

Feng Fuping1,Deng Ping2,Xing Jun3,Lyu Yuanyuan4,Zhang Ji′nan5
(1.College of Petroleum Engineering,Northeast Petroleum University,Daqing 163318,China;2.Research Institute of Engineering Technology,Xinjiang Oilfield Company,PetroChina,Karamay 834000,China;3.Daqing Oilfield Engineering Company Limited, PetroChina,Daqing 163712,China;4.Research Institute of Petroleum Exploration and Development,Liaohe Oilfield Company, PetroChina,Panjin 124010,China;5.Science and Technology Department,Jilin Oilfield Company,PetroChina, Songyuan 138000,China)

The interface shape of cementing displacement reflects the intermixing extent of two-phase fluids and decreasing the length of displacement interface will be helpful to improve the displacement effect and annular cementing quality.Due to the change of driving force caused by the density difference between slurry and drilling fluid with the position of fluid microelement on the displacing profiles in horizontal well,the local advance of displacing interface will happen even in a steady-state displacement.As a result,the length of displacing interface will be increasing gradually.In this paper,a calculation model that describes the interface shape of steady-state displacement has been derived through considering the change of driving force with annular circumferential angle and radius and using the two-dimension Hele-Shaw displacement model and perturbation theory.Besides,it analyzes the change of interface length with density difference in the horizontal well with eccentric casing,which provides an important basis for designing slurry and drilling fluid density and decreasing the length of displacement interface.

horizontal well;casing eccentricity;steady-state displacement;interface shape;density difference;displacement model

国家自然科学基金项目“考虑周向二次流对顶替界面影响的固井二维顶替模型研究”（51404071）

TE256

：A

10.6056/dkyqt201501027

2014-06-23；改回日期：2014-11-14。

冯福平，男，1982年生，博士，2005年毕业于大庆石油学院石油工程专业，主要从事油气井工程力学方面的教学和科研工作。E-mail：fengfuping2005@163.com。

冯福平，邓平，邢均，等.水平井偏心环空稳定顶替界面形状研究［J］.断块油气田，2015，22（1）：120-125.

Feng Fuping，Deng Ping，Xing Jun，et al.Research on interface shape of steady-state displacement in eccentric annulus of horizontal well［J］. Fault-Block Oil&Gas Field，2015，22（1）：120-125.