致密油藏直井体积压裂非稳态产能评价模型

姜龙燕，荀小全，王楠，杨帆

（1.中国石化华北石油工程有限公司测井分公司，河南 新乡 453000；2.中国石化华北分公司勘探开发研究院，河南 郑州 450006；3.中国石油辽河油田分公司勘探开发研究院，辽宁 盘锦 124010；4.中国石化华北分公司第一采油厂，甘肃 庆阳 745000）

致密油藏直井体积压裂非稳态产能评价模型

姜龙燕1，荀小全2，王楠3，杨帆4

（1.中国石化华北石油工程有限公司测井分公司，河南 新乡 453000；2.中国石化华北分公司勘探开发研究院，河南 郑州 450006；3.中国石油辽河油田分公司勘探开发研究院，辽宁 盘锦 124010；4.中国石化华北分公司第一采油厂，甘肃 庆阳 745000）

基于渗透率区域分形和动边界法，文中建立了一种可用于致密油藏直井体积压裂改造非稳态产能评价的解析模型。模型考虑了人工裂缝网络展布及启动压力梯度的影响，并应用已建立的模型对分形系数、启动压力梯度、改造半径（等效于改造体积SRV）等影响产能的参数进行了分析。结果表明：分形系数只对初期产能有影响且影响很大，分形系数负值越大，体积压裂改造越彻底，初期产能越高；启动压力梯度对整个生产期都有影响，对后期产能影响尤为突出，启动压力梯度值越大，产能越低，双对数曲线越晚趋于平缓；改造半径也对整个生产期都有影响，对前期产能影响要远大于后期，改造半径越大，产能增加越显著。这为合理开发致密储层及体积压裂改造优化设计提供了一定的参考。

致密油藏；体积压裂；非稳态产能；分形；启动压力梯度；SRV

0 引言

近年来，随着能源市场需求的不断增大及压裂技术的长足进步，致密油藏开发已然成为国内外研究热点之一，油气田开发重心逐渐由高质量、易开发类型向低质量、难动用类型转移。中国有着丰富的致密油资源，初步预测总量约为1.1×1010t，是当前较为现实的接替能源［1-2］。

致密油储层渗透率超低（上覆岩石压力下小于0.1×10-3μm2），采用常规单一裂缝增产改造措施不足以达到工业生产要求，需求大型体积压裂改造形成裂缝网络从而增大单井产能［3-5］。裂缝传导率及裂缝半长作为参数已不足以评价体积压裂改造后生产井的产能，需要将储层改造程度及缝网的空间展布（从微地震图可以看出制造的裂缝网络近似一个三维体积）也看作评价参数，参与描述井的生产情况。

目前，国外很多学者基于数值模拟对体积压裂改造井进行了研究。比如：K.M.Al-Salem［6］，C.L.Cipolla［7］以及B.Rubin［8］采用纵横正交的裂缝网络替代体积改造区域进行模拟；A.K.Harikesavanallur［9］根据微地震结果，设置改造区域渗透率值来实现近似模拟；C.Du［10］借用双重介质加以描述改造区域等。相比之下，国内起步较晚［11-16］，有关体积压裂产能的研究较少，且主要有以下2方面缺陷：1）与解析方法相比，数值模拟虽然能够应对复杂的渗流问题，但很大程度上受网格划分及运算方法的限制，不能考虑启动压力梯度的影响，使用也不够简便；2）到现在为止，还没有可用于致密油藏直井体积压裂改造产能评价的解析模型被提出。

1 物理模型

1.1 假设条件

直井体积压裂改造控制区域可以分为内部区域和外部区域2个部分（见图1）。

受储层岩石脆性及人工裂缝改造的影响，内部区域布满了纵横交错不规则的剪切裂缝网络。由于剪切裂缝网络改变了该区域的渗流模式，以裂缝导流为主，基质供应流体速度远远小于裂缝运输能力，因此，本文假定整个裂缝与井筒构成的系统在任意时刻都能随着井筒和复合边界压力瞬时达到稳态，且不考虑该区域启动压力梯度的影响。由于多重压裂不确定性及地层在不同方向应力的不尽相同，形成的裂缝网络不会沿着半径方向均匀展布，也有可能只有部分区块受到压裂改造形成裂缝网络。为此，本文使用渗透率分形来描述体积压裂形成的裂缝网络对该区域的改造情况［14］。

外部区域没有受人工裂缝改造，随着直井开始生产，压力从内部区域的外边界开始向外传播，而启动压力的存在限定了压力传播的范围，因此，可利用动边界方法来描述这一非稳态压力传播过程。

基于以上讨论，模型基本假设条件包括（以下推导过程中物理量都使用达西混合单位制）：1）储层均质、各向同性，体积改造形成的缝网沿半径均匀分布；2）启动压力梯度是个定值，不随位置变化而变化；3）考虑介质及流体的微可压缩性。

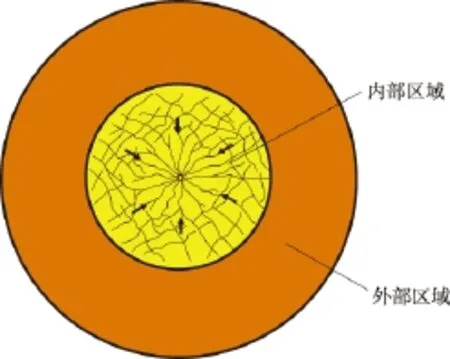
图1 体积压裂直井二维平面示意

1.2 数学模型

已知圆形致密油藏中心有一口定产生产井，体积压裂改造区域渗透率满足（见图2）：

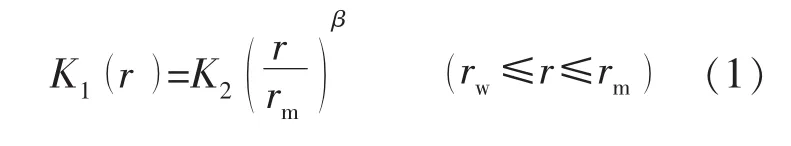
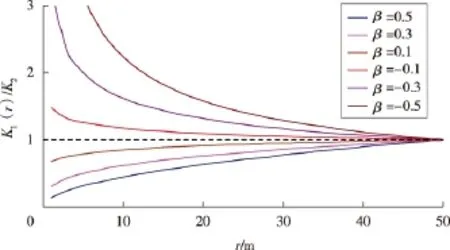
图2 不同β值对应的体积压裂改造区域渗透率分布情况

1.2.1 外部区域

对单相平面径向渗流，根据物质平衡原理，连续性方程满足：

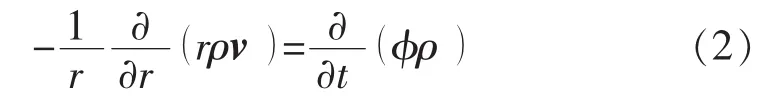
考虑G的影响，运动方程可以表示为

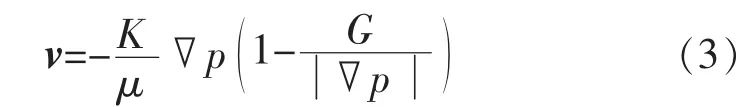
考虑介质及流体微可压缩性，状态方程为

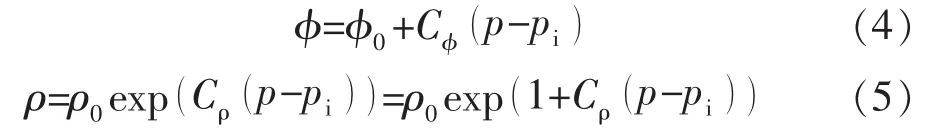
将运动方程及状态方程代入连续性方程，忽略（▽p）2项：

将有关参数无量纲化：

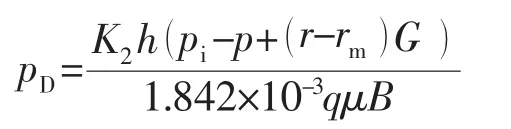
则式（6）可以转化为

初始条件：

内边界定产条件：

外边界条件：

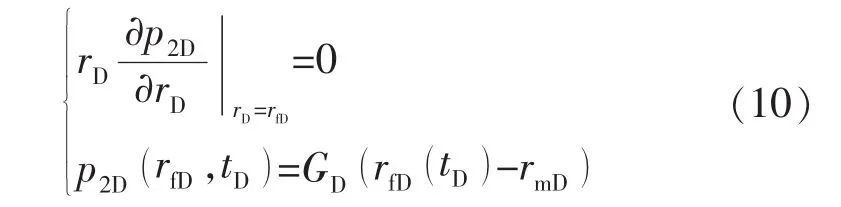
1.2.2 体积压裂改造区域

不考虑启动压力梯度的稳态压力分布公式为

从式（11）可以得到耦合边界处的压力表达式：

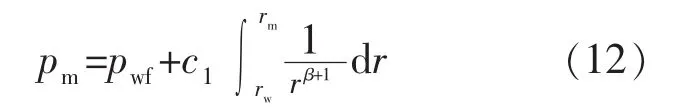
求解式（11）可以得到c1值，代入式（10），得

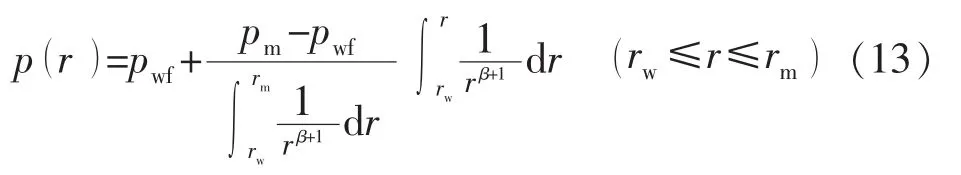
代入内边界条件，可以得到产量表达式：

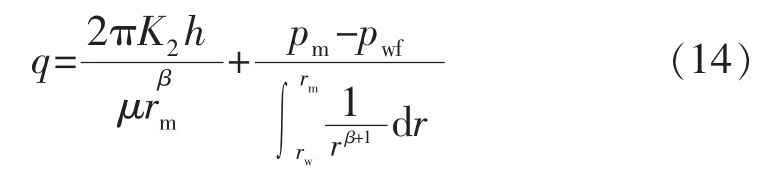
对式（14）积分整理可以得出：

无量纲化得到：

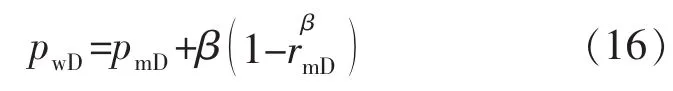
式（16）经Laplace变换为

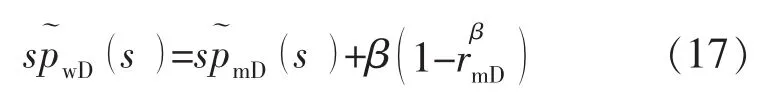
2 模型求解

式（7）经Laplace变换为

内边界条件经Laplace变换为

外边界条件经Laplace变换为

将式（19）和式（20）代入式（22），可以得到：

联合求解式（23）和式（24），可以得到：

代入式（22）得到拉式空间压力分布解：

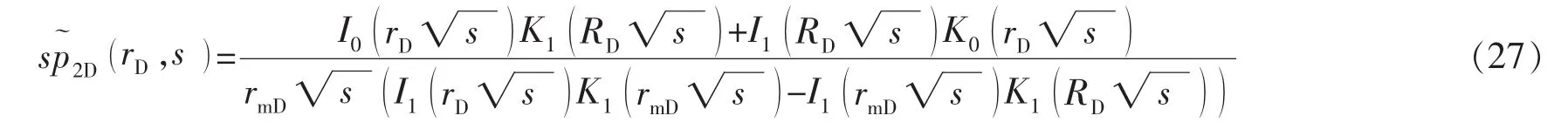
将式（27）代入式（21），可得式（18）上面有关动边界传播的表达式：

由式（27）可以得到耦合边界处Laplace压力解：

结合式（29）和式（17），可以得到Laplace井底压力表达式为

则Laplace定压条件下井底产能表达式为

3 影响参数分析

根据式（28）及式（31）的推导结果，利用Stehfest数值反演［17］可以计算出动边界随时间推移的传播情况及分形系数、启动压力梯度、改造半径3个参数与产能之间的关系曲线（见图3）。

图3 不同GD及rmD条件下rfD-tD的关系

由图3可以看出：随着无量纲时间的推移，无量纲启动压力梯度越大，对应的无量纲动边界值越小，表明生产井压力向外传播范围越小，井控泄流面积也越小；内部区域改造半径大小直接决定初始无量纲动边界位置，随无量纲时间推移，不同改造半径对应的无量纲动边界逐渐趋于一致。

3.1 分形系数

分形系数的大小，表示体积压裂改造区域裂缝网络改造程度的高低，负号表示储层得到改善，正号代表储层受到污染。GD=0.010 0，rmD=10时，不同分形系数下，无量纲产量与无量纲时间的双对数曲线对比见图4。由图可以看出分形系数只对初期产能有影响，且影响很显著，分形系数取值越大，即直井体积改造越彻底，初期产能越高。

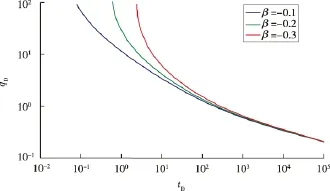
图4 分形系数对产能的影响

3.2 启动压力梯度

β=-0.1，rmD=10时，不同启动压力梯度下，无量纲产量与无量纲时间双对数曲线见图5。由图可以看出：启动压力梯度的存在，对整个生产过程的产量都有影响，且对后期影响要强于初期；启动压力梯度越大，产能越低，无量纲产量与无量纲时间的双对数曲线越到后期越趋向于平缓。

图5 启动压力梯度对产能的影响

3.3 改造半径

改造半径是描述体积压裂改造大小的一个评价参数。β=-0.1，GD=0.010 0时，不同改造半径条件下，无量纲产量与无量纲时间的双对数曲线见图6。由图可以看出，改造半径在整个生产期对产能都有影响，其对前期产能的影响要远大于后期，改造半径越大，改造油藏体积越大，产能增加越显著。

图6 体积压裂改造半径对产能的影响

分形系数与改造半径分别体现了直井体积压裂的改造程度和改造体积。从分析结果可以看出，这2个因素对前期产能都有很大影响，说明体积压裂作为有效的增产措施对生产前期的作用效果是非常显著的。

4 结论

1）分形系数对初期产能的影响最大。分形系数负值越大，说明裂缝网络改造得越彻底，初期产能越高。

2）启动压力梯度对整个生产周期的产能都有影响，对后期产能影响尤为突出。启动压力梯度越大，产能越低。

3）改造半径在整个生产期对产能都有影响，对前期影响要远大于后期，改造半径越大，产能增加越明显。

4）有效压裂改造体积对生产井前期增产效果非常显著。

5 符号注释

q为产量，m3/d；μ0为流体初始黏度，mPa·s；ρ0为初始密度，kg/m3；φ为储层孔隙度，%；h为储层厚度，m；r为离生产井的径向距离，m；rw为井半径，m；rm为复合边界半径，m；rf（t）为动边界，m；pi为原始地层压力，MPa；pwf为井底流压，MPa；G为启动压力梯度，MPa/m；K1，K2分别为内、外部区域渗透率，10-3μm2；β为分形系数；ρ为流体密度，g/cm3；v为渗流速度，cm3/s；t为时间，s；K为储层渗透率，10-3μm2；p为压力，MPa；φ0为储层初始孔隙度，%；Cφ为孔隙压缩系数；Cρ流体黏度系数；p2为外部区域r对应的压力，MPa；Ct为综合压缩系数；c1为常数；A，B为系数；下标1，2分别代表内、外部区域。

［1］南珺祥，王素荣，姚卫华，等.鄂尔多斯盆地陇东地区延长组长6—8特低渗透储层微裂缝研究［J］.岩性油气藏，2007，19（4）：40-44.

［2］郭彦如，刘俊榜，杨华，等.鄂尔多斯盆地延长组低渗透致密岩性油藏成藏机理［J］.石油勘探与开发，2012，39（4）：417-425.

［3］贾承造，邹才能，李建忠，等.中国致密油评价标准、主要类型、基本特征及资源前景［J］.石油学报，2012，33（3）：343-350.

［4］邹才能，朱如凯，吴松涛，等.常规与非常规油气聚集类型、特征、机理及展望：以中国致密油和致密气为例［J］.石油学报，2012，33（2）：173-187.

［5］李玉伟，艾池，张博文，等.同步体积压裂对井间裂缝特性的影响［J］.断块油气田，2013，20（6）：779-782.

［6］Al-Salem K M，Ali M A M，Lin C.Tight oil reservoir development feasibility study using finite difference simulation and streamlines［R］. SPE 126099，2009.

［7］Cipolla C L，Lolon E，Mayerhofer M J.Reservoir modeling and production evaluation in shale-Gas reservoirs［R］.IPTC 13185，2009.

［8］Rubin B.Accurate simulation of non darcy flow in stimulated fractured shale reservoirs［R］.SPE 132093，2010.

［9］Harikesavanallur A K，Deimbacher F，Crick M V，et al.Volumetric fracture modeling approach（VFMA）：Incorporating microseismic data in the simulation of shale gas reservoirs［R］.SPE 134683，2010.

［10］Du C，Zhang X，Zhan L，et al.Modeling hydraulic fracturing induced fracture networks in shale gas reservoirs as a dual porosity system［R］. SPE 132180，2010.

［11］王文东，赵广渊，苏玉亮，等.致密油藏体积压裂技术应用［J］.新疆石油地质，2013，34（3）：345-348.

［12］王文东，苏玉亮，慕立俊，等.致密油藏直井体积压裂储层改造体积的影响因素［J］.中国石油大学学报：自然科学版，2013，37（3）：93-97.

［13］刘雄.致密油储层体积改造产能评价方法研究［D］.北京：中国地质大学，2013.

［14］刘雄，田昌炳，姜龙燕，等.致密油藏直井体积压裂稳态产能评价模型［J］.东北石油大学学报，2014，38（1）：91-96.

［15］王文雄，李帅，刘广峰，等.致密油藏体积压裂建模理论与方法［J］.断块油气田，2014，21（4）：492-496.

［16］葛家理，宁正福，刘月田，等.现代油藏渗流力学原理［M］.北京：石油工业出版社，2003：189-194.

［17］Stehfest H.Algorithm 368：Numerical invesion of Laplace transforms［J］.Communications of the ACM，1970，13（1）：47-49.

（编辑 朱丽）

Non-steady state productivity evaluation model of volume fracturing for vertical well in tight oil reservoir

Jiang Longyan1,Xun Xiaoquan2,Wang Nan3,Yang Fan4
(1.Logging Company,Huabei Petroleum Engineering Company Ltd.,SINOPEC,Xinxiang 453000,China; 2.Research Institute of Exploration and Development,Huabei Company,SINOPEC,Zhengzhou 450006,China; 3.Research Institute of Exploration and Development,Liaohe Oilfield Company,PetroChina,Panjin 124010,China; 4.No.1 Oil Production Plant,Huabei Company,SINOPEC,Qingyang 745000，China)

Based on fractal permeability area and moving boundary method,a non-steady state productivity evaluation analytical model being available for the volume fracturing for vertical well in tight oil reservoir is established.The model takes the effect of artificial fracture network distribution and threshold pressure gradient into consideration.Some parameters,such as fractal coefficient,threshold pressure gradient and reconstruction radius(equivalent to SRV),are analyzed by using the established model. The results show that fractal coefficient only has obvious influence on initial productivity.The greater fractal coefficient negative value is,the more thoroughly reconstruction of volume fracturing is and the higher initial productivity is.Threshold pressure gradient has effect on whole production period,especially on later productivity.The greater threshold pressure gradient value is,the lower productivity is and the later log-log type curve turns to smooth-out.Reconstruction radius also has effect on whole production period, but especially on initial productivity.The larger reconstruction radius is,the higher productivity is,which has a certain reference value for reasonable development and volume fracturing of tight reservoir.

tight oil reservoir;volume fracturing;non-steady state productivity;fractal;threshold pressure gradient;SRV

国家科技重大专项课题“CO2驱油与埋存关键技术”（2011ZX05016-006）

TE357

：A

10.6056/dkyqt201501018

2014-09-15；改回日期：2014-11-20。

姜龙燕，女，1987年生，助理工程师，硕士，2013年毕业于中国地质大学（北京）矿产普查与勘探专业，现主要从事测井与油气田开发研究工作。E-mail：sunshine_jly@163.com。

姜龙燕，荀小全，王楠，等.致密油藏直井体积压裂非稳态产能评价模型［J］.断块油气田，2015，22（1）：82-84.

Jiang Longyan，Xun Xiaoquan，Wang Nan，et al.Non-steady state productivity evaluation model of volume fracturing for vertical well in tight oil reservoir［J］.Fault-Block Oil&Gas Field，2015，22（1）：82-84.