让思维之花开满课堂——“图形中的规律”课例与分析
2015-02-20安徽省六安市三里桥小学黄玉芹
□安徽省六安市三里桥小学 黄玉芹
让思维之花开满课堂——“图形中的规律”课例与分析
□安徽省六安市三里桥小学黄玉芹
【摘要】为发展小学生的数学思维能力,激发学生学习数学的兴趣,使其体会数学思想、锻炼思维能力、积累思考经验,首先要通过数学课堂所设置的活动让学生能够思考起来,在发现规律的过程中,让学生在描述规律的基础上,尝试解释自己是如何发现这个规律的。
【关键词】数学思维数形结合发展能力
【教学内容】北师大版小学五年级数学上册“图形中的规律”(教材第97~98页)。
【教学目标】
1.观察发现点阵中的规律,体会“图形与数”的联系。
2.进一步培养归纳、推理和概括的能力。
3.感受“数形结合”的魅力,发现数学的神奇之美,体验“我能发现”的成功之美。
【教学重点】
1.学生多角度探究规律、发现规律,充分感受“美图美思”。
2.在画一画、算一算中,大胆说出自己的发现。
3.以独立研究为主,辅以合作交流。重视知识理解,鼓励学生猜想。
【课堂写真】(节选)
活动三:从不同的角度观察,发现点阵中新的规律。
1.师(课件再次出现4个点阵图):除了“横看、竖看”,大家能不能尝试用不同的方法去观察呢?你们还能用其他的方法划分正方形点阵吗?
(课件出示活动要求:用线画出不同的划分方法,并用算式表示每个点阵的点数。请学生齐读要求,教师强调要运用不同的划分方法)
2.学生独立完成,在练习纸上画出自己的想法,并写出相应的算式。
(注:学生有的用斜线划分,有的用折线划分)
3.同桌交流后,学生展示汇报。
(1)展示交流学生的第一种方法。

师:我看见不少同学都至少有一种想法了。请一位同学将自己的观察方法画在白板上,并介绍一下自己的方法。
生1:我是用斜线进行划分的。
师:你这种划分方法能得出怎样的算式呢?
生1(结合点阵图进行介绍):第二个点阵图可以用算式1+2+1来表示,第三个点阵图是1+2+3+2+1,第四个点阵图就是1+2+3+4+3+2+1。
(教师板书算式,请学生观察)
师:你有什么发现?
生1:第2个点阵中间数是2,第3个的中间数是3,第4个的中间数是4。
生2:第几个点阵就加到几,然后再从那个数加回1。比如第3个点阵,从1加到3,再从3加回到1;第4个点阵,从1加到4,再从4加回到1。
师:你能快速说出第五个点阵图的算式吗?
生2:1+2+3+4+5+4+3+2+1。
小结:斜看的规律,就是从1开始连续自然数相加,加到第几个点阵数再倒回去加回到1。
(2)展示交流学生的第二种方法。
师:这组正方形点阵还有其他的规律吗?
(请学生在白板上画,这位同学在每个点阵上用折线画出了后一个点阵比前一个点阵多出的部分)
(注:这名学生的画法,说明他是通过点阵之间的横向比较,看出还可以用折线划分的)
生1:我是用折痕划分。可以起名叫折线划分。
师:你的这种方法可以用怎样的算式表示呢?
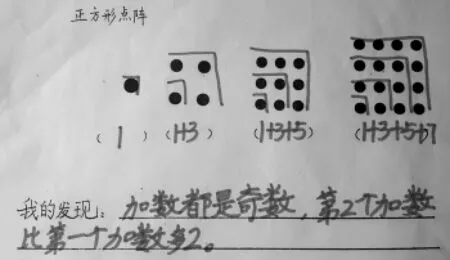
生1:第一个点阵就用1表示,第二个点阵就用1+3,第三个点阵就是4+5。
师:这里的4你可以用1+3表示吗?
(学生立即在第三个点阵上补画出折线,写出算式:1+3+5,并很快写出第四个点阵是1+3+5+7)
师:仔细观察这种折线划分方法得出的算式,有什么发现吗?
生1:是奇数。
生2:是连续的奇数。
生3:是第几个点阵就加几个连续的奇数。
师:能具体说说吗?
生3:比如说,第三个点阵就要加三个连续的奇数,算式是:1+3+5;第四个点阵就要加四个连续的奇数,算式是:1+3+5+7。
师:那第五个点阵呢?
生3:1+3+5+7+9。
4.观察比较。
(补充板书,完整出示三种不同的划分方法得出的三组不同的算式,请学生仔细观察)
师:刚才我们用了几种方法来观察这组正方形点阵?
生:四种。
师:哪四种?
生:横看,竖看,斜看,折线看。
师:横看、竖看可以用同样的算式表示。请观察这三组算式,有什么发现?
生:三组算式得出的得数都是一样的。
师:为什么都一样呢?
生1:因为它们划分的是同一个点阵图。
生2:因为我们观察的是同一个正方形点阵图。
师:用了三种不同的划分方法,得出了三种不同的算式,归纳出了三种不同的规律,但归根结底我们研究的是同一个正方形点阵、同一个数,所以用点阵来研究数的形式可以是多种多样的。
(注:学生通过观察交流得出三种不同的划分方法的相同点和不同点。通过具体详细的例证得出:虽然划分方法不同、算式不同,即隐含的规律不同,但表示的是相同的数,说明通过点阵研究数的形式可以是多样的)
【说明与反思】
一、从本次教学中我学到的东西及前后几次试教的体会
在教学折线划分这一环节时,对于学生来说,是个难点,很多学生很难发现新的规律。为了突破难点,让学生能发现折线划分的方法,在第一次试教时,我做了一个教具,将每一个点阵图用一种颜色的圆点表示出来。当第一个点阵放在第二个点阵的上面时,第二个点阵比第一个点阵多出来的三个点就看得非常清晰,再将第三个点阵放在前两个点阵的后面,那么第三个点阵多出来的五个点就成一个直角排列,再让学生按照这个方法将正方形点阵进行划分。学生给这种划分方法起名叫“直角看”。之后再引导学生观察后一个点阵比前一个点阵多几个点,从而得出从1开始连续奇数相加的算式,归纳出算式中隐藏的规律:第几个点阵就从1开始加几个连续的奇数。
在第二次试教时我还设计了一个动手环节,让小组合作剪一剪、画一画。我提出剪的要求是:在第二个点阵中将第一个点阵剪下来,在第三个点阵中将第二个点阵剪下来。两个同学剪,另外两个同学按照他们剪的路线在点阵图中画出来。在学生动手操作过后,很容易发现每一个点阵比前一个点阵多出来的点都成直角排列。画出折线这种方式,让学生在动手的过程中发现“折线看”或者“拐弯看”的方法。这种方法尝试以后,发现这个环节占用的时间太长,影响教学任务的完成。同时,老师在这里“暗示”,没有真正放手让学生思考、观察。过后我问自己:“这种折线看的方式学生真的就很难发现吗?需不需要花费大量的时间在这个环节上?”
在这里我总是纠结,总是害怕学生发现不了“我想要的规律”。
再次试教四版教材时,我豁然开朗:通过主情境的铺垫,学生已经了解到后一个点阵总比前一个点阵多了一行一列,在这里教师只要做稍微的点拨,学生就很容易发现折线的划分方法。然后,分小组讨论交流:折线划分后,可以用怎样的算式表示,探究算式中所蕴藏的规律。通过课堂实践来看,本节课已经落实了课前制定的学习目标。
二、在本节课中如何促进学生进行数学思考
1.让学生“能思考”。“数学是自己思考的产物,首先要能够思考起来。”上完这节课后,课堂上的情节依然还在脑海中盘旋,挥之不去。尤其是“斜线观察”和“折线观察”这两个活动,让我思考颇多。在我看来,这恰是这堂课的关键之所在。在生活和数学中,存在着大量的有规律的事物,以及事物变化趋势的问题。这些问题的解决没有现成的固定的模式,更多的是要通过探索、归纳、猜想、解释,最后验证得到结果。我就是要试图通过这个十几分钟的片段来说明这个问题。
2.让学生“会思考”。用自己的见解和别人的见解交换,会有很好的效果。学生经过前面的学习,已经为后面的“斜线观察”和“折线观察”的学习积累了经验,打下了基础。除了“横看”、“竖看”,还可以怎么看?通过合作讨论,学生把“‘纸’转过来、调过去,歪着头、抓耳挠腮……”经过这个“阵痛”,学生发现:原来同一个点阵,还可以这样看——“斜看”和“直角看”(这是学生创造的名词,在我第一次试教的时候“蹦出来的”)。学生的思维火花碰撞出新的结果,这也算有了一种“很好的结果”吧。
3.让学生“有时间思考”。在前面学生学习“横看”、“竖看”,我只是一带而过,因为学生自己可以不要费什么劲儿,这样我把时间留给后面的“斜线观察”和“折线观察”,特别是“拐弯看”,让学生“有时间思考”。我用一句“还可以怎么看”,把学生的思维“转个弯”,发散学生的思维,让节奏慢下来。“是啊,还可以怎么看呢?”学生进入了“另一个思考程序”。有一位大家说过:学习过程,不应当像暴风骤雨般拳击比赛的过程,而应当像那舒缓连绵的打太极的过程。学生在“斜线观察”和“折线观察”后,我又引导学生“用算式表示出来”,学生发现:观察方法不同,算式表现的形式不同,但是表示的结果却是相同的。
当然我说的这些,有的我们(我、学生、同事)已经在实践中验证了,有的还在进行中。相信借力优秀的北师版教材,通过团结在北师版周围的优秀专家们的引领,加上我们广大师生的努力,思维之花会进一步绽放,我们的课堂一定会开满思维之花!
(此文在第十三届新世纪小学数学课程与教学案例研究暨第七届中国——瑞典数学教育论坛中荣获一等奖。指导教师:王林,特级教师,中学高级教师)
