改进的中值滤波在图像去噪中的应用
2015-02-19唐诗华
陈 晓,唐诗华
(1.桂林理工大学 测绘地理信息学院,广西 桂林 541004;2.广西空间信息与测绘重点实验室,广西 桂林 541004)
随着电子科学技术的高速发展,数字图像已经成为日常生活中不可缺少的一部分,是人类获取信息,传递信息的一条重要渠道。但是由于设备自身的缺陷和环境的影响,获取的图像中含有噪声[1,2]。而由于噪声的影响,数字图像本身会变得模糊,不能准确地获取图像的相关信息,给后续的处理带来很大的难度,为了得到高质量的数字图像,去噪就显得尤为重要。目前,去噪的方法有2大类,线性滤波和非线性滤波[3,4]。而在非线性滤波中,中值滤波由于其具有较好的去噪效果而被广泛使用[5]。
1 中值滤波和软阀值法的去噪原理
中值滤波是基于排序统计理论的一种能有效去除噪声的处理技术。中值滤波的原理就是把数字图像中一点的灰度值用该点的一个邻域中各点值的中值代替,从而消除孤立的噪声点[6,7]。可表示为:

式中,g(x,y)、f(s,t)表示处理后图像和原图像;N(x,y)是以(x,y)为中心的n×n矩形滤波窗口(n为奇数);med{}为图像的灰度值按照大小排序后,取中间的值。例如,n=5,设有序列{1,0,6,4,3},那么med{1,0,6,4,3}=3。
小波的软阀值去噪就是先通过小波变换对小波系数进行处理,然后再通过小波逆变换重构图像,得出去噪后的图像[8,9]。可表示为:
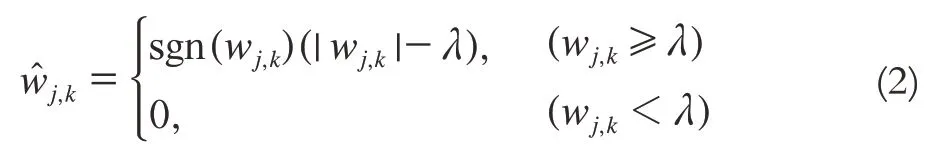
式中,wj,k为处理前的小波系数;wtj,k为处理后的小波系数;λ为阀值。
2 改进的中值滤波
标准的中值滤波和软阀值法在去噪方面都取得了一定的效果,但还存在一些不足。中值滤波在去噪时,不能很好地保护图像的边缘,使得一些细节信息丢失。而软阀值法会使得估计的小波系数与原小波系数之间存在较大的恒定偏差。针对这些问题,提出一种改进的中值滤波算法。
根据中值滤波的原理,在滑动窗口向左移动一个像素的距离时,窗口的最后边增加了一列像素值,而最左边的一列像素值退出滑动窗口,其他的像素值保持不变。也就是说,影响中值,只是最右和最左的2列像素值。设窗口的尺寸大小为3×3,窗口移动一个像素距离时,最右的像素值为(x,y,z),此时最左的像素值为(i,j,k)。当同时满足条件x=i、y=j、z=k时,中值保持不变,原值输出;而当其中有一个式子不成立时,中值就会改变。这时候就用新的值代替不等的值,同时求出窗口中所有像素点的新均值。利用标准的中值滤波,对所有新的灰度值进行排序,得出新的中值,然后对新的中值和新的均值进行加权处理,所得的值赋给中心点。接着窗口继续向前移动一个像素,重复上面的步骤,直到图像处理完成。
3 实验结果分析
文中以Matlab7.11.0作为实验平台。对原始图像加入高斯噪声,方差取0.02。中值滤波中,选用5×5的滤波窗口。用上述3种方法所处理得到的图像,如图1~5所示。

图1 原图像

图2 加噪声图像

图3 中值滤波法

图4 软阀值法

图5 改进的中值滤波法
图1为原图像,图2为加入方差为0.02的高斯噪声图,图3、图4分别为中值滤波法和软阀值法处理后的图像,图5是改进的中值滤波法处理的效果图。从视觉上看,3种方法都能有效地去除图像的噪声,图5相对于图3、图4来说,去噪的效果更好,而且轮廓更加清晰,细节更加细腻,对图像的边缘保护更好一些。为了更客观地评价这3种方法的优劣性,分别计算3 种方法的信噪比PSNR:

式中,u(m,n)为原图像的灰度值;v(m,n)为图像去噪后的灰度值;M和N分别为横向与纵向像素的个数。根据式(3)可以得出:PSNR标中值=75.836;PSNR软阀值=76.261;PSNR改中值=80.135。从计算结果来看,标准的中值滤波法和软阀值法所得出的信噪比平分秋色,而改进后的中值滤波在信噪比方面比前面2种方法有了较大的提高,这是由于重新计算出中值和灰度均值,并对新的中值和新的均值进行加权处理,所得的值赋给中心点。因此得出的图像比较清楚,在能有效去噪的同时,也能较好地保护图像的细节,增强图像的可读性,为后续处理提供良好的基础。
4 结 语
图像去噪的好坏决定了数字图像质量的高低,本文通过标准中值滤波、软阀值法、改进的中值滤波3种方法的仿真,结果表明,改进的中值滤波不仅能有效地去除噪声,而且能较好地保护图像边缘的细节,具有更好的去噪性能。
[1]罗玲,王修信.一种高效去除椒盐噪声的中值滤波方法[J].微电子学与计算机,2011,28(11):118-121
[2]王秀芳.数字图像的噪声及其去噪的几种方法研究[J].黑龙江科技信息,2010,28(6):53-55
[3]刘伟.自适应中值滤波在数字图像处理中的应用[J].河北理工大学学报,2007,11(4):111-113
[4]Gallagher N C, Wise G L.A Theoretical Analysis of Properties of the Median Filters[J].IEEE Transactions on Acoustics Speech,Signal Processing,1981,29(1):1 136-1 141
[5]孙海英,李锋,商慧亮.改进的变分自适应中值滤波算法[J].电子与信息学报,2011,33(7):1 743-1 747
[6]赵高长,张磊,武风波.改进的中值滤波算法在图像去噪中的应用[J].应用光学,2011,32(4):679-680
[7]张燕.一种改进的快速中值滤波算法[J].安微建筑工业学院学报:自然科学版,2008,16(4):24-26
[8]谢杰成,张大力,徐文立.小波图像去噪综述[J].中国图像图形学报,2002,7(3):209-217
[9]文鸿雁,张正禄.非线性小波变换阀值法去噪改进[J].测绘通报,2006(3):18-21
