基于调频调幅信号EMD分解去噪效果的仿真研究

陆人定

(常州信息职业技术学院　江苏常州　213164)



基于调频调幅信号EMD分解去噪效果的仿真研究

陆人定

(常州信息职业技术学院江苏常州213164)

摘要：在仿真基础上，对旋转机械调频调幅振动信号EMD分解去噪效果进行了分析，总结出了EMD分解的SD值大小对信号去噪效果的影响，提出了SD值过小虽然可以增加含噪信号迭代次数，最大程度去噪，但会破坏原信号的局限性。论证了采用适当SD值的EMD分解与滤波结合能有效地去噪并提取特征信号。

关键词：EMD分解； 调频调幅信号； 迭代次数

信号处理中，EMD[1]分解方法由美籍华人Norden E.Huang等人创立，在各个行业中获得了广泛的应用，在雷达波地质探测[2]、机械振动信号检测[3]、电力电子检测[4]、音视频处理技术[5-6]、地震波检测[7]，都取得了一定的效果，该方法将信号基于本身局部特征进行分解，提取信号特征或去除信号噪声。

齿轮箱旋转机械系统如大型汽车变速器、风力发电机组齿轮箱、大型纺织企业齿轮箱系统往往包含上百个齿轮、传动轴、轴承。当某个齿轮发生故障时，技术人员很难立即判断出故障部位发生在何处。工程技术界内，通过故障信号的解调分析技术[8]可以有效地判断出故障部位，但前提条件是信号能量最好要大于噪声能量，即信噪比SNR>0，否则不能提取有效地故障信息。

从数学模型分析，齿轮故障齿轮箱振动信号表现为周期性的异常冲击，以齿轮啮合频率为载波频率，以故障齿轮所在轴的转频为调制频率的调制现象，且其信号为调频调幅信号[8]，本文尝试引入EMD分解法最大限度去掉旋转机械调频调幅振动信号中的噪声，并作相关的仿真分析。

1调频调幅信号信噪比SNR变化对于提取故障特征信息影响

对于加噪声调制信号，如果噪声很大，则不能对信号进行平方解调分析[8]。以调频调幅信号加高斯白噪声为例，用matlab软件，仿真信号如公式(1)：

x(t)=[1+cos(2π20t)]cos[2π300t+sin(2π20t)]

(1)

采样频率900 Hz，采样点数1 024点，分别取信噪比SNR=0.5和SNR=-0.5。

如图1所示，加噪声调频调幅仿真信号分别取信号能量大于噪声能量(SNR=0.5，能解调出特征频率20.21 Hz)及信号能量小于噪声能量(SNR=-0.5，不能解调出特征频率)。仿真说明，信噪比SNR大小对信号分析有举足轻重的影响，噪声能量过大，将不能提取特征信息。因而EMD分解去除噪声算法有广阔的应用范围，下面作进一步分析。

图1SNR=0.5与SNR=-0.5加噪声信号平方解调谱

2EMD去噪分解对含噪声调频调幅信号局限性分析

2.1　EMD去噪分解算法对加噪声单频信号的影响

为了更加简洁明了地说明问题，先以单频信号为例，分析SD值[1]对EMD去噪效果的影响。

如图2，仿真信号加噪声信号x(t)=cos(2π20t)，采样频率1 000 Hz，采样点数4 096点，SNR=-0.5。如图3所示，SD=0.2时第5个IMF分量就可以分出单频信号20 Hz，如图4所示，SD=0.02时，第12个IMF分量才分解出20 Hz信号，且单频信号能量已经被分解了损耗。通过仿真分析，得出如下结论：

1)SD值直接反映信号被EMD分解迭代次数，SD值越小，EMD分解迭代次数越多。

2)信号中噪声能量越大，即SNR值越小，为了达到最大程度去噪，EMD值分解时，要求SD值越小，则信号被迭代次数越多，信号才能更好地去掉噪声。

3)含噪声单频信号在单频率附近能量是最高的，SD值越小，信号被迭代次数越多，虽然噪声最大程度去掉了，但使各个IMF分量能量强制平均化，因此极有可能将单频信号能量分离，从而淹没在各个含噪声的IMF分量里，削弱了真实有用的特征信号。

图2　SNR=-0.5加噪声单频信号幅值谱与频谱

图3　SD=0.2时，迭代5次分解出的

图4SD=0.02时，迭代12次分解出单频

信号幅值谱与频谱

2.2　EMD分解对理想不含噪声的旋转机械类调频调幅信号分解局限性

如公式(2)所示，调频调幅信号可看作三个频率成分交叉的纯调频信号叠加。

x(t)=[1+cos(2π40t)]cos[2π400t+sin(2π40t)]

(2)

其中，f1为调制频率，f11为载波频率，其他为常系数。

如图5，仿真信号如公式(3)：

x(t)=[1+cos(2π1t)]cos[2π10t+2sin(2π1t)]

(3)

采样频率30 Hz，采样点数1 024点。

通过仿真分析，得出如下结论：

1)调频调幅信号是一种宽频率信号，可看作是以调频载波频率为中心频率，以调制频率为间隔的一簇频率带的叠加[8]，如图5所示，x(t)可看作是三个中心频率分别为9 Hz，10 Hz，11 Hz，1 Hz为调制频率的三个调频宽频带的结合体。

2)SD=0.2时，略小，如图6所示，与原信号图5对比，x(t)被迭代次数较多，信号能量被平均化，原信号被破坏，产生假频成分多。

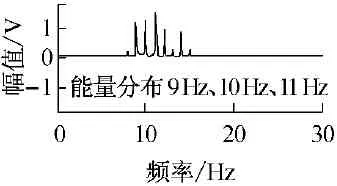
图5 仿真信号x(t)原幅值谱

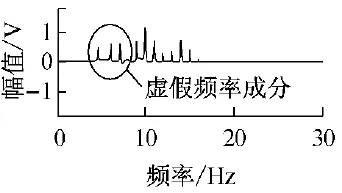
图6 SD=0.2,迭代产生假频成分

3)SD=0.02时，过小，信号被迭代次数过多，如图7所示，原信号x(t) 被严重破坏，被分解成了中心频率分别为10 Hz与11 Hz的两个调频信号，典型的过度分解。

图7SD=0.02，过度迭代把原信号x(t)错误

分解成了两个调频带

综上所述，对于调频调幅信号，SD值不能过小，否则过度迭代会破坏原信号，会分解出虚假频率成分，甚至会把原信号分解成多个信号，产生严重错误。

3将滤波与EMD分解结合对加噪声调频调幅信号去噪并解调

理论上，EMD分解去噪能力是不如带通滤波去噪能力的，但滤波法对带通范围内的信号进一步去噪无能为力，此时可用EMD进一步去噪，提高信号的信噪比，从而提高解调分析能力。

取仿真信号x(t)公式(4)，如图8所示，

x(t)=[1+cos(2π40t)]cos[2π400t+sin(2π40t)]

(4)

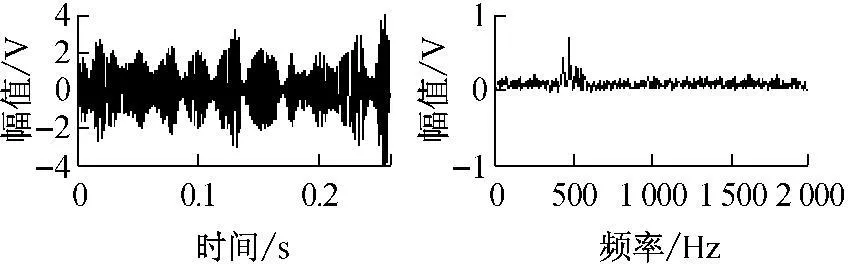
图8SNR=-0.5的加噪声调频调幅

信号x(t)幅值谱与频谱

采样频率4 000 Hz，采样点数1 024点，分别取信噪比SNR=-0.5。采用滤波器加EMD分解联合去噪声法，滤波器下限频率为0 Hz，上限频率为1 200 Hz，EMD分解SD=0.2。

如图9所示，右边图只用滤波器去噪的解调谱上难以分辨调制频率，左边图采用EMD和滤波器联合去噪后能有效地分析出调制频率成分39.06 Hz。

4结束语

1)信噪比SNR大小对信号去噪效果有举足轻重的影响，噪声能量太大，任何去噪算法都无效果。EMD和滤波法只适用于噪声能量不太大信号。

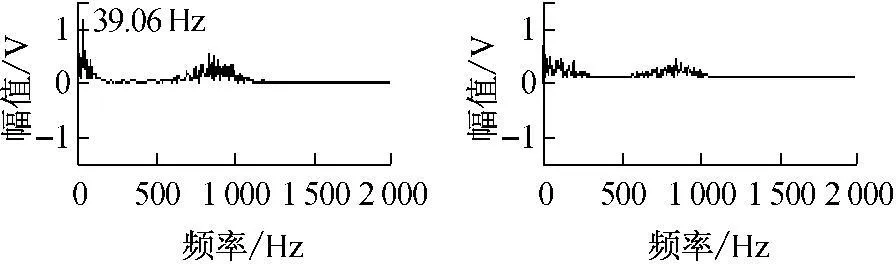
图9采用EMD、滤波联合去噪与滤波单独去噪解调谱

2)EMD分解对信号的去噪有一定效果，但SD值越小，往往会出现过度迭代现象，计算量大大增加，各IMF分量能量平均化，真实信号成分将被平均分配到噪声里，会破坏分解出虚假频率成分，甚至会把原信号分解成多个信号，产生严重错误。因此SD值不能过小。

3)信号EMD分解的去噪效果不如滤波器，但EMD分解能对滤波器带通范围内的信号进一步去噪，提高信噪比，更利于解调分析，提取故障特征信号。

以上分析仅限于旋转机械循环平稳调频调幅信号，其他特征信号有待进一步探讨。

参考文献：

[1]Huang, N. E, Shen, Z.,Long,S.R.,etc. The pirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. The Rayal Society, 1998(454): 903-995.

[2]陈凯. 基于经验模式分解的去噪方法[J]. 石油地球物理勘探, 2009(5)： 603-608.

[3]曹冲锋. 基于EMD的机械振动分析与诊断方法研究[D]. 杭州: 浙江大学， 2009： 34-40.

[4]孙金宝, 朱永利, 刘丽轻, 等. 基于EMD的绝缘子泄漏电流去除噪声研究[J]. 华北电力大学学报： 自然科学版， 2010(6)： 1-5.

[5]秦宇强， 张雪英. 语音信号中基于EMD法的情感计算[J]. 数学的实践与认识， 2011(5)： 123-128.

[6]李烨. 基于EMD的图像拼接和图像识别研究与实现[D]. 重庆： 重庆交通大学， 2010： 24-34.

[7]杨培杰， 印兴耀， 张广智. 希尔伯特—黄变换地震信号时频分析与属性提取[J]. 地球物理学进展， 2007(10)： 1585-1590.

[8]丁康, 李巍华, 朱小勇. 齿轮及齿轮箱故障诊断实用技术[M]. 北京: 机械工业出版社， 2005: 91-108.

Simulation Study on EMD Decomposition

De-noising Effect based on AMFM signal

LU Ren-ding

(Changzhou College of Information Technology, Changzhou 213164, China)

Abstract：Based on the simulation, this paper makes an analysis on EMD decomposition de-noising effect based on AMFM signal. It summarizes the impact of SD value of EMD decomposition on the signal de-noising effect, and presents that small SD value could increase the number of iterations, but the original signal would be destroyed. This paper demonstrates that the EMD decomposition of appropriate SD value in combination with filtering could effectively reduce noise and select characteristic of signal.

Key words：EMD decomposition; AMFM signal; number of iteration

中图分类号：TN 911.4

文献标志码：A

文章编号：1672-2434(2015)01-0020-03

作者简介：陆人定(1981-)，男，工程师，主要研究方向：汽车电子技术、嵌入式开发

收稿日期：2014-10-23