一类非线性梁方程全局吸引子的维数估计

姜金平,张晓明,董超雨

(延安大学 数学与计算机科学学院,陕西 延安　716000)



一类非线性梁方程全局吸引子的维数估计

姜金平,张晓明,董超雨

(延安大学 数学与计算机科学学院,陕西 延安716000)

摘要:非线性梁方程描述了桥面竖直平面内的振动.在以往文献的基础上证明了一类非线性梁方程生成的解半群S(t)在全局吸引子Α上是一致可微,其全局吸引子具有有限的分形维数，并进一步应用Sobolev-Lieb-Thirring不等式进行估计，得到全局吸引子的分形维数的上界.

关键词:非线性梁方程;全局吸引子;一致可微;分形维数

文[1]作者研究了如下非线性梁方程

(1)

其中:u(x,t)描述了桥面在竖直平面内的变形,δ表示粘性阻尼,h∈L2(Ω),u1,u2为给定的初值.

文[1]中假设Ω⊂R2是具有光滑边界∂Ω的有界区域,用一种新的验证紧性的方法讨论了方程(1)的强解及全局吸引子的存在性,然而此类方程吸引子的维数估计的研究几乎没有,而作者将证明这类方程生成的解半群的一致可微性和全局吸引子具有有限的分形维数并用与文献[2-3]中相似的方法给出这类梁方程的维数估计,这恰好填补了梁方程维数估计研究的空白.

关于非线性函数g∈C2(R,R)假设满足下面的条件

文[1]中证明了半群{S(t)}t≥0在E0和E1中的连续性,并且还证明了在条件(H1)~(H3)成立的情况下,由(1)式生成的解半群{S(t)}t≥0在E1中存在全局吸引子Α,它以E1的范数吸引E1中的任意有界集.

则定义的空间是Hilbert空间.另外,∀s,r∈R,Ar是从D(As)到D(As-r)的同构,特别地,A是从D(As)到D(As-1)的同构,且存在α>0,使得

(2)

1预备知识

定理1[4-5](Sobolev-Lieb-Thirring不等式)假设Ω是Rn中的有界开集,边界是Cm且满足可延拓性质,|Ω|表示Ω的体积.如果φj,1≤j≤N是Hm(Ω)中的函数组并且在L2(Ω)中正交,则

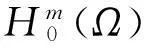
定义1[6-7]半群S(t)在全局吸引子Α上一致可微是指,对任意u∈Α,存在线性算子Λ(t,u),使得对所有t≥0,有

当ε→0,并且

定义,其中:Pn是到有限维投影算子.

可以看出,如果Tr(L(s;u0)Pn(s))有一致的界,即

则

如果TRn(Α)<0,那么n维体积微元指数衰减,具体的证明由B.Hunt在1999年给出.在应用中,只要找到使TRn(Α)为负的n,就可以给出吸引子的维数上界df(Α)≤n.

定理2[6]设半群S(t)在全局吸引子Α上是一致可微的且存在时间t0,使得对所有t>t0是紧的.如果TRN(Α)<0,则df(Α)≤N.

2吸引子的维数估计

为了证明(1)全局吸引子Α的维数有界性,需要检验定义1与定理2.下面先检验定义1.

∀u1∈Α,方程(1)在u(t)=S(t)u1的线性化方程为

(3)

∀ξ∈H,易知方程(3)存在唯一解U(x,t)∈C(0,T;V)∩C(0,T;H),∀T>0.为方便起见,记

则(3)简记为

(4)

引理1设g(u)满足给出的条件,并且是C2的,n≤3,则(1)式生成的解半群{S(t)}t≥0在Α上是一致可微的,即对任意u∈Α,存在线性算子Λ(t,u),使得对所有t≥0,有

证明设u(t),v(t)是(1)的解,初值分别是u1,v1∈Α,U(t)是(4)的解,初值为v1-u1.令θ(t)=v(t)-u(t)-U(t),则

(5)

其中：ε=2-q(1+δ)>0.

另一方面,由标准方法得|u-v|≤eMt|u1-v1|,所以，‖h‖Lq≤Ce(1+r)Mt|u1-v1|1+r.用θ和(5)作内积得

而由文献[1]知〈Aθ,θ〉≥α‖θ‖2,|g′(u)|L∞≤K3,得

由文献[8]中的方法可得‖θt‖2在L∞(Ω)中一致有界,则λ‖θt‖2≤R(R为常数),所以

由Gronwall不等式得

所以,S(t)一致可微.

下面对算子Λ(t,u1)进行估计,其中:Λ(t,u1)ξ=U(t),U(0)=ξ.对(4)与U作内积,有

所以

(6)

丢掉左边第二项得

由Gronwall不等式,有

即

(7)

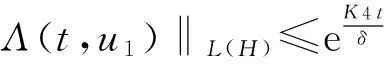
即S(t)满足定义1中一致可微的条件.

(8)

下面验证|Λ(t,u1)|是紧算子,∀t>0.即|Λ(t,u1)|把有界集映成紧集.

对(4)与ΔΔU作内积得

下面估计Tr(F′(u(τ))·QN(τ))

(9)

下面估计(9)右边第一项,主要用到Sobolev-Lieb-Thirring不等式,由文献[1]知n=2,m=2,可得

(10)

所以,(9)变为

参考文献：

[1]马巧珍,孙春友,钟成奎.非线性梁方程强全局吸引子的存在性[J].数学物理学报:A辑,2007,27(5):941-948.

[2]赵春山,李开泰.二维全空间上线性阻尼Navier-Stokes方程的全局吸引子及其维数估计[J].应用数学学报,2000,23(1):90-98.

[3]张天佑,穆春来,邢庭莉.一类模式演化方程的全局吸引子及其维数估计[J].重庆大学学报:自然科学版,2007,30(3):79-82.

[4]Takeuchi S,Yokota T.Global attractor for a class of degenerate diffusion equations[J].Electronic Journal of Differential Equation,2003,76:1-13.

[5]Temam R.Infinite-dimensional dynamical systems in mechanics and physics[M].New York:Springer-Verlag,1997.

[6]Robinson J C.Infinite-dimensional dynamical systems an introduction to dissipative parabolic PDEs and the theory of global attractors[M].Cambridge:Cambridge University Press,2001.

[7]郭柏灵.无穷维动力系统[M].北京:国防工业出版社,2000.

[8]Colucci R,Chacon G R.Dimension estimate for the global attractor of an evolution equation[J].Abstract and Applied Analysis,2012，18(10)：541-556.

(责任编辑朱夜明)

Dimension estimate for global attractor of a class of nonlinear beam equation

JIANG Jin-ping, ZHANG Xiao-ming, DONG Chao-yu

(College of Mathematics and Computer Science,Yan’an University,Yan’an 716000,China)

Abstract:The nonlinear beam equations represent the viberation of the rode bed in downward direction.Based on the existence of global attractors in other article,this paper proved that semigroup S(t) generated by a class of nonlinear beam equation was uniformly differentiable on the global attractor Α.The paper also proved that global attractors of this class of equation have limited fractal dimension.Furthermore,an estimate was given with the application of Sobolev-Lieb-Thirring inequality and upper bound of fractal dimension of the global attractor is obtained.

Key words:nonlinear beam equation;global attractor;uniform differentiability;fractal dimensions

作者简介：毛北行(1976-),男,河南洛阳人,郑州航空工业管理学院副教授.

基金项目:国家自然科学基金资助项目(51072184);国家自然科学基金数学天元基金资助项目(11226337);河南省科技厅基础与前沿研究计划项目(142300410410);郑州航空工业管理学院青年基金资助项目(2014113002)

收稿日期：2014-09-12

doi:10.3969/j.issn.1000-2162.2015.02.003

中图分类号：O175

文献标志码:A

文章编号:1000-2162(2015)02-0008-05