归纳推理与类比推理的比较
2015-02-19郑州幼儿师范高等专科学校翟金成
郑州幼儿师范高等专科学校 翟金成
归纳推理与类比推理的比较
郑州幼儿师范高等专科学校翟金成
中图分类号:G42
文献标识码:A
文章编号:1671-864X(2015)03-0103-02
合情推理是数学的基本思维过程,也是人们学习和生活中经常使用的思维方式。在解决问题的过程中,合情推理具有猜侧和发表结论,探索和提供思路的作用。有利于创新意识的培养。在学习中要把推理方法形成自己的解决问题的意识,使得问题的解决有章有法,得心应手。合情推理包括归纳推理和类比推理。
一、归纳推理和类比推理的联系
归纳推理与类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理。由这两种推理得到的结论都不一定正确,其正确性有待进一步证明。
二、归纳推理和类比推理的区别
(一)归纳推理
1.归纳推理定义∶由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理(简称归纳)。简言之,归纳推理是由部分到整体、由个别到一般的推理。
说明:归纳推理的思维过程大致如下:

2.归纳推理的特点∶
(1)归纳推理的前提是几个已知的特殊现象,归纳所得的结论是尚属未知的一般现象,该结论超越了前提所包容的范围。
(2)由归纳推理得到的结论具有猜测的性质,结论是否真实,还需经过逻辑证明和实践检验。因此,它不能作为数学证明的工具。
(3)归纳推理是一种具有创造性的推理.通过归纳推理得到的猜想,可以作为进一步研究的起点,帮助人们发现问题和提出问题。
归纳推理是从个别事实中概括出一般原理的一种推理模型,归纳推理包括不完全归纳法和完全归纳法。
3.归纳推理的一般步骤:
①通过观察个别情况发现某些相同本质;
②从已知的相同性质中推出一个明确表达的一般性命题。
说明:归纳推理基于观察和实验,像“瑞雪兆丰年”等农谚一样,是人们根据长期的实践经验进行归纳的结果.物理学中的波义耳—马略特定律、化学中的门捷列夫元素周期表、天文学中开普勒行星运动定律等,也都是在实验和观察的基础上,通过归纳发现的。
(二)类比推理(以下简称类比)1.类比推理定义∶由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比)。简言之,类比推理是由特殊到特殊的推理。
2.类比推理的一般步骤:
①找出两类事物之间的相似性或一致性;
②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想)。
3.说明:类比推理的思维过程大致如下图所示:

类比推理是在两类不同的事物之间进行对比,找出若干相同或相似点之后,推测在其他方面也可以存在相同或相似之处的一种推理模式。类比推理不象归纳推理那样局限于同类事物,同时,类比推理比归纳推理更富于想像,因而也就更具有创造性。人类在科学研究中建立的不少假说和教学中许多重要的定理,公式都是通过类比提出来的,工程技术中许多创造和发明也是在类比推理的启迪下而获得的。因此,类比推理已成为人类发现发明的重要工具。
三、典例剖析
例1.观察下列等式∶
12=1
12-22=-3
12-22+32=6
12-22+32=-10
照此规律,第n个等式可为____.
本例是利用归纳推理解决问题的,作为归纳推理的“集散地”,以数列为背景是常见的命题形式,通过数列呈现的规律来确定数列的某一项,具有一定的难度,且具有时代性。考察观察、归纳、推理能力。
由归纳推理所得到的结论不一定正确,但它所具有的特殊到一般的性质对数学的发展有着十分重要的作用,应用时首先分析清楚题目的条件,合理归纳.
例2.求一个质数,当它分别加上10和14时仍为质数.
【分析】我们可以采用归纳推理,先由具体的数计算开始,再归纳猜想一般性的结论.
【解析】用归纳法进行试验∶
2+10=12,2+14=16,质数2不合要求;
3+10=13, 3+14=17,质数3不合要求;
5十10=15,5+14=19,质数5不合要求;
7+10=17, 7+14=21,质数7不合要求.
……
归纳上述结论,可以猜想,3是符合要求的质数.
联想发散∶归纳推理是通过对一些个别、特殊情况的观察与分析,导出一般结论的推理方法,利用归纳猜想,可以探索数学规律,探究解题途径。但是结论的正确性还有待于逻辑上的证明。本题中由于质数的变化无规律,不能用解析式把它表示出来,因此若能证明除了3之外的所有自然数分别加上10和14不能都是质数,也就证明了除3以外的所有质数加上10和14不能都是质数.事实上,自然数可分为三类3n , 3n+1,3n+2(n足正整数);∵(3n+1)十14=3(n十5)是合数;(3n十2)+10=3(n+4)是合数;
∴3n+1和3n+ 2这两类自然数中的质数都不符合要求,而3n这类自然数中,只有当n=1时,3n才能是质数,其余都是合数,因此符合条件的质数只有3.
例3.如图,过四面体V-ABC的底面上任一点O分别作OA1∥VA,OB1∥VB,OC1∥VC,A1,B1,C1分别是所作直线与侧面交点。求
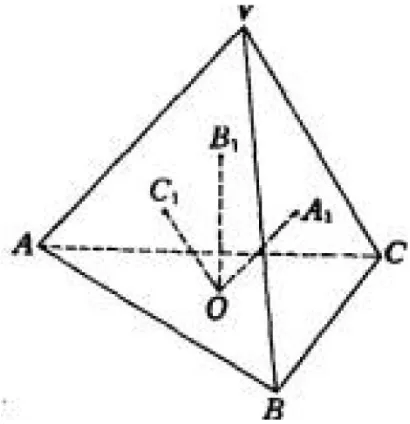
【分析】考虑平面上的类似命题:“过△ABC(底)边AB上任一点O分别作OA1∥AC,OB1∥BC,分别交BC、AC于A1、B1,求证为定值”.这一命题利用相似三角形性质很容易推出其为定值1.另外,过A、O分别作BC垂线,过B、O分别作AC垂线,则用面积法也不难证明定值为1.于是类比到空间围形,也可用两种方法证明其定值为1.
【证明】如图,设平面OA1 VA∩BC=M,平面OB1 VB∩AC=N,平面OC1 VC∩AB=L,则有△MOA1∽△MAV,△NOB1∽△NBV,△LOC1∽△LCV.得。
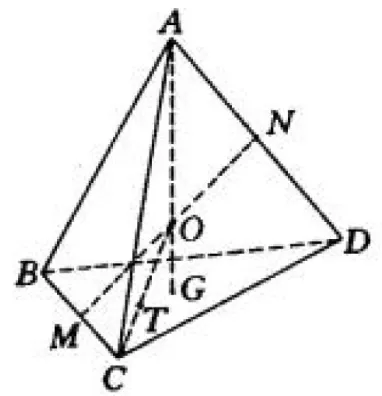

在底面△ABC中,由于AM、BN、CL交于一点O,用面积法易证得:。
通俗地说,合情推理是指“合乎情理”的推理。数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论;证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向。
