U钻上T形刀片的受力分布数学模型分析

■山东光岳转向节有限责任公司 （聊城 252000） 杨宝亮 吕建魁

U钻上T形刀片的受力分布数学模型分析

■山东光岳转向节有限责任公司 （聊城 252000） 杨宝亮 吕建魁

摘要：通过对T形刀片可转位浅孔钻的受力分析，提出以径向力平衡作为浅孔钻的设计原则，基于金属切削原理，利用微积分思想建立内外刃刀片的受力数学模型，推导出内外刃刀片的受力分布情况。

机夹硬质合金刀片浅孔钻又称为U钻，此种钻头刀杆刚度高，允许切速高，加工精度高，普遍应用于数控机床。根据钻头孔径的不同，所配备的刀片数量也不同。U钻多数装沉孔刀片，采用压孔方式夹紧。钻头由刀体、刀片、压紧螺钉、模块及定位销等组成。刀体尾部与机床的联接采用圆柱柄、莫氏锥柄及7∶24 锥柄等。刀体上有进油孔，通过Y形油路进入切削区。当以钻头回转为主运动时，需用冷却环供应切削液（见图1）。

1. 力学分析

U钻所用刀片的形状为四边形、三边形及六边形等。在直径为18mm 的50U钻上通常安装两个刀片，内外刀片搭接，把被加工孔径分成四个部分、两个步骤（见图2）。当内刃刀片不过钻头回转中心时，若采用三边形刀片时（T形），钻削中只产生切削力Fq和进给力Fj（见图3），没有背向力。进给力影响机床进给机构的设计及刀体弯曲强度的选择；由于两刀片的不对称分布，导致切削力在刀体上产生径向合力FH和周向合力矩TH（见图4）。径向合力易导致实际钻削轴线与理论加工路线产生偏离，影响被加工孔的尺寸公差和形位公差；周向合力矩可通过与机床的旋转力矩匹配得以平衡，防止钻体断裂。因此，最大限度地减小加工时的径向合力FH，就成了浅孔钻设计与制造的关键问题。

2. 数学分析

为了便于U钻的受力分析，把外刃位置与内刃位置移至同一侧进行考虑（先不考虑搭接量）（见图5）。由于T形刀片钻削的受力情况，类似于毛坯端面车槽的情况。依据金属切削机理，U钻刀片的切削力与ap（背吃刀量）、f（进给量）及v（切削速度）成正比。根据微积分原理建立钻削力数学模型如下（见图6）。

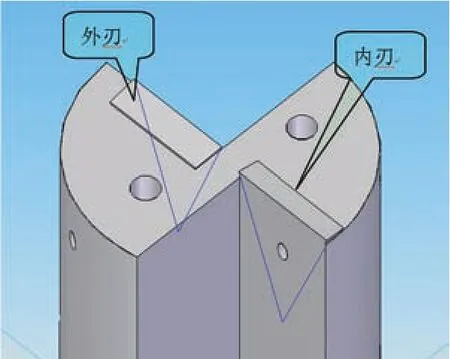
图1　示意图

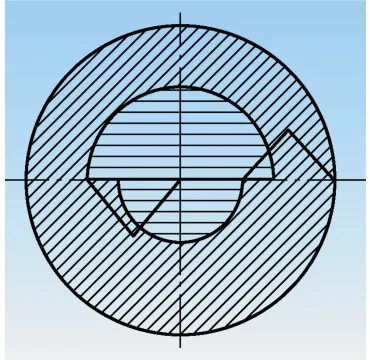
图2　内外刃切削区

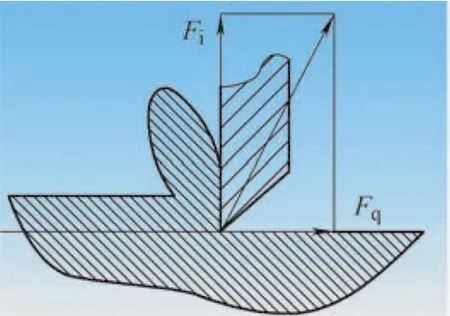
图3　切削受力图

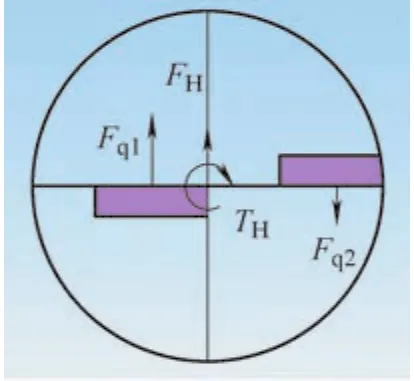
图4　受力合成图

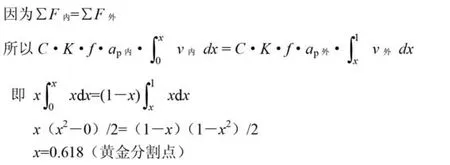
3. 结构布置

从以上分析可知，两个切削边长度不同，在不考虑搭接量的情况下，内外刃边长比列为0.618∶0.382。为了便于设计制造，经优化设计搭接量可取0.13，则比例为0.75∶0.51（此结果仅用于装配T形刀片的U钻钻头）。

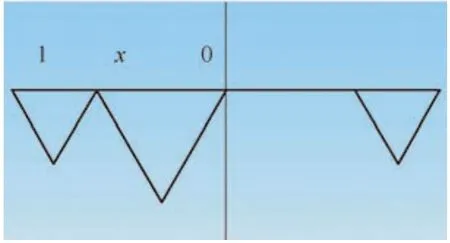
图5　数学分析图

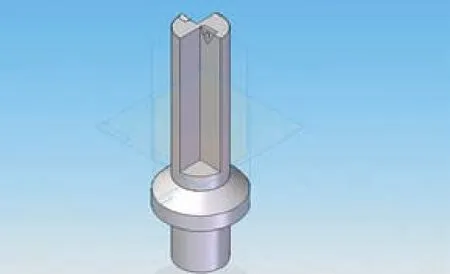
图6　模拟图

收稿日期：（20150104）