车辆-轨道-路基垂向耦合模型研究综述

周广新　周　颖

(同济大学土木工程防灾国家重点实验室, 上海 200092)



车辆-轨道-路基垂向耦合模型研究综述

周广新周颖*

(同济大学土木工程防灾国家重点实验室, 上海 200092)

摘要我国有关高速铁路动力学问题的研究已基本采用耦合动力学方法,而不再是传统的孤立系统动力学分析方法。为方便相关领域科研人员熟悉各种耦合动力学模型以解决高速铁路运营中的实际问题及指导施工,首先从轮轨动力、轨道模型、车辆模型及路基参振四个方面回顾了车辆-轨道-路基垂向耦合模型的发展历史,从模型实际应用及模型与有限元软件结合和试验验证两个方面介绍了车辆-轨道-路基垂向耦合模型的发展现状,总结了车辆-轨道-路基垂向耦合模型的发展趋势,通过归纳整理,指出有限元软件中纳入车辆系统、建立创新的“两半车”模型将是车辆-轨道-路基垂向耦合模型新的发展方向。

关键词高速铁路, 动力响应, 垂向耦合模型, 综述

State-of-the-art of the Vehicle-track-subgrade Model ofVertical Coupled System

ZHOU GuangxinZHOU Ying*

(State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

AbstractThe research on the dynamic response of high-speed railway in our country has already been studied by the method of coupling dynamics, and no longer the traditional method of independent system dynamics.Aiming at providing reference for related scholars to have a good grasp of various coupling dynamics models to solve existing practical problems and efficiently guide the construction of high-speed railway, this paper reviewed the development history of the vehicle-track-subgrade model of vertical coupled systems, including the wheel/rail dynamic interaction, the improvement of track model and vehicle model and the participation of subgrade in vibration. The state of the art of the vehicle-track-subgrade model of vertical coupled systems, including the practical application and the combination with finite element software and test technique, was introduced. It is pointed out that modeling of vehicle system in finite element software and development of innovative “two-halves vehicle” model will be the trends of the vehicle-track-subgrade model of vertical coupled system.

Keywordshigh-speed railway, dynamic response, vertical coupled model, state-of-the-art

1引言

铁路是我国主要运输方式,在国民经济中起着非常重要的作用,是国民经济发展的先导[1]。近年来发展了高速铁路,其具有运行速度快、运输能力大、能源消耗低、环境影响轻、土地占用少、安全性好、正点率高等综合优势,在许多国家得到了迅速发展。

然而,高速铁路的快速发展在带来一系列经济和社会效益的同时,也同样带来了一些问题。目前,我国处于高速铁路建设大发展时期,人们对高速列车荷载作用下轨道路基动力问题越来越关注。而随着京沪高铁、沪杭客运专线的修建和开通运营,高速铁路在软土地区的路基沉降变形问题日益突出。如何评价和确保软土地区高铁路基长期服役性能,是目前面临的重大问题。因此,十分有必要对求解高速铁路动力问题的各种理论模型进行总结概括,归纳各种模型特点及发展历史,为评价高速铁路运营性能及指导施工提供参考。

国内外很多文献对列车动荷载作用下轨道或路基的动力响应等问题作了阐述,但长期以来,针对轮轨系统动力学的研究一直是分开进行的,由此形成了车辆动力学、轨道动力学以及路基动力学等几个相对独立的学科领域。经典的车辆系统动力学以车辆系统为研究对象,视轨道系统为“刚性支承”(即刚性固定边界),不考虑轨道系统对车辆系统的动态影响,而将轨面几何不平顺视为车辆系统的外部激扰,研究车辆运行安全性与平稳性[2-4];经典的轨道动力学常常将车辆简化为轨道系统的外部激振荷载(定点激励或移动荷载),分析轨道结构振动特性及其变形特征[5-7]。在路基动力学里,则单独研究路基在上部荷载作用下的动力响应(如沉降变形、应力应变等)及荷载的传递规律。

然而,基于轨道与路基之间力与变形相互协调这一事实,单独分析轨道结构与单独分析路基、地基结构不能满足两者之间的相容条件,因此,国内外很多学者[8-11]研究了轨道与路基之间的耦合作用。此外,随着现代高速铁路交通运输的飞速发展,特别是列车运行速度、运载重量和运输密度的大幅提高,车辆与轨道之间的动态相互作用更加突出,因此发展了具有更为全面计算分析功能的车辆-轨道-路基耦合作用理论模型。

本文首先从轮轨关系、轨道模型、车辆模型以及路基参振等方面回顾了车辆-轨道-路基垂向耦合模型的发展历史,介绍了车辆-轨道-路基垂向耦合模型的发展现状,总结了车辆-轨道-路基垂向耦合模型的发展趋势,并对车辆-轨道-路基垂向耦合模型的发展方向进行了展望。

2车辆-轨道-路基垂向耦合模型发展历史

2.1　轮轨动力

如前所述,传统的孤立系统动力学分析方法致使高速铁路振动问题不能明确地求解。

进入20世纪70年代,铁路运输业的迅猛发展以及计算机技术的广泛应用极大地推动了轮轨相互作用的研究。英国Derby铁路技术研究中心开展的轨道接头处轮轨动作用力试验与理论研究,标志着轮轨动力作用的研究进入了实质性阶段。1972年,Jenkins等[12]建立了轮轨动力相互作用分析的基本模型(图1),研究了车辆与轨道基本参数(如簧下质量、轨道刚度等)对轮轨作用力的影响。在该模型中,轨道视为连续弹性基础支承的欧拉梁,将车辆简化为簧下质量,并考虑一系悬挂特性,轮轨接触采用目前较成熟的Hertz非线性弹簧接触模型。

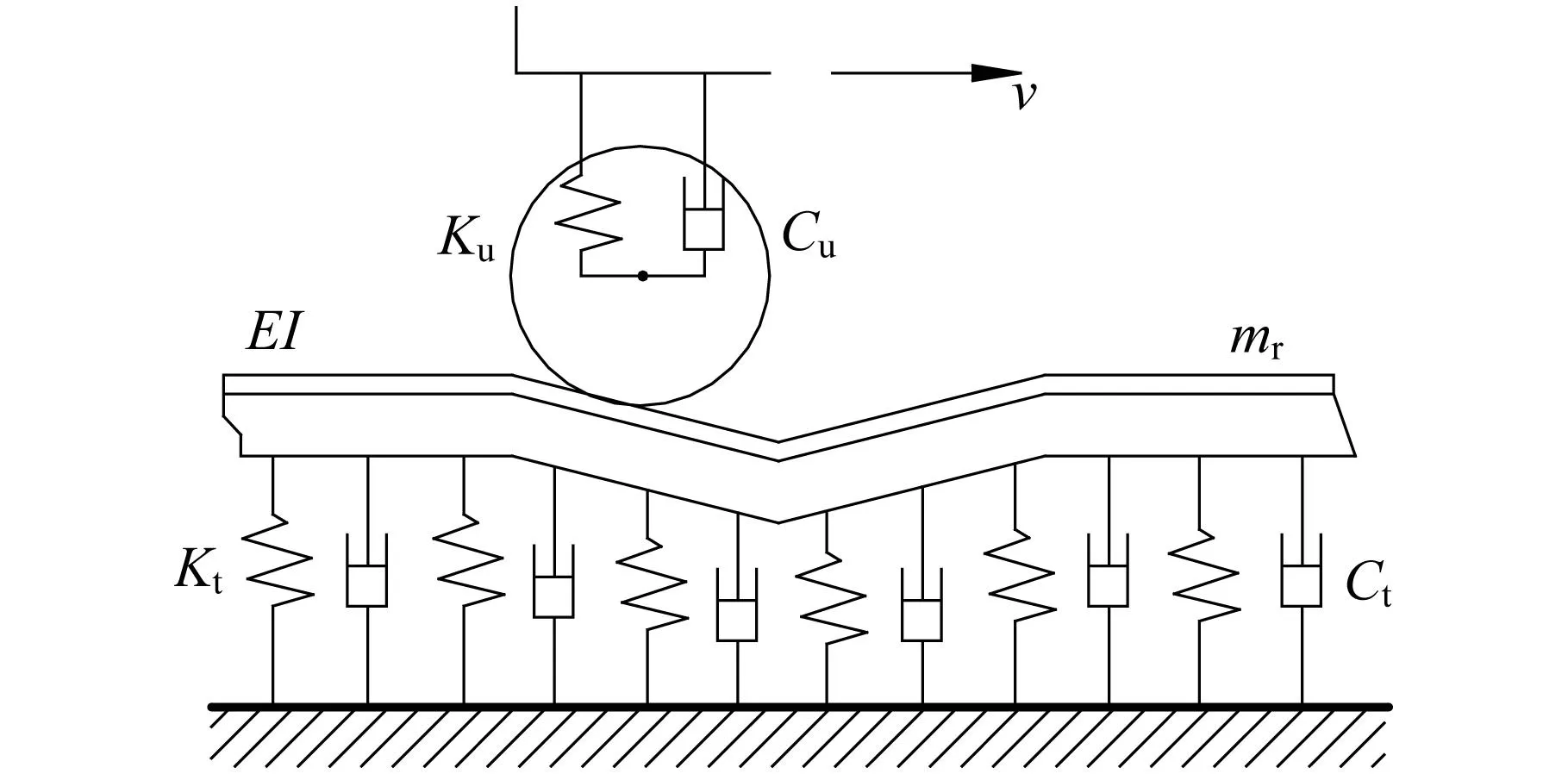
Ku、Cu—车辆悬挂刚度与阻尼;Kt、Ct—轨道支承刚度与阻尼;EI—钢轨抗弯刚度;mr—钢轨单位长质量;v—车辆运行速度图1　最基本的轮轨动力分析模型[12]Fig.1　The basic model of dynamic analysis forwheel-rail interaction [12]

1979年,Newton等[13]在研究车轮踏面擦伤对轨道的动力作用时,考虑钢轨的剪应变,以Timoshenko梁代替欧拉梁,取得与试验一致的理论结果。

同一时期,日本学者佐藤裕和佐藤吉彦做了大量的轮轨动力分析,提出具有代表性的Sato“半车-轨道”集总参数模型[14],如图2所示。

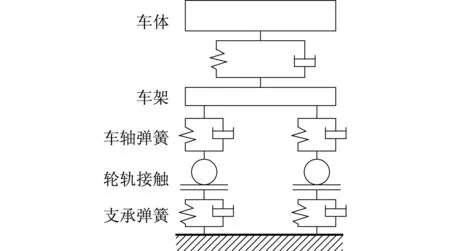
图2　“半车-轨道”集总参数模型[14]Fig.2　The half-vehicle/rail lumped parameter model [14]

我国学者在轮轨动力分析模型方面开展了一系列研究工作。文献[15]采用最简单的轮轨集总参数模型计算了轨道低接头处轮轨冲击力(图3),文献[16]利用有限元方法分析图1模型,文献[17]采用文克尔地基上的Timoshenko梁模拟分析了钢轨接头处的轮轨作用力。

图3　最简单的轮轨集总参数分析模型[15]Fig.3　The simplest wheel/rail lumped parameter model [15]

2.2　轨道模型

结构振动分析中,最早发展起来的是多刚体系统的振动分析方法,因此轨道振动分析中,最早也是将轨道简化为由质量、弹簧和阻尼组成的多刚体模型[18],这类模型称为集总参数模型。图2及图3中,轨道视为单自由度模型,根据模型精细程度的不同,可建立轨道二自由度集总参数模型甚至多自由度集总参数模型,考虑轨枕、道床等的参振[18]。

显然,集总参数模型无法客观地反映钢轨作为抗弯梁的工作特性,计算中的各种参数很难接近实际状态且不易确定。1867年,文克尔(Winkler)提出弹性地基梁理论,这一理论很快用于轨道的建模。1926年,铁木辛柯(Timoshenko)应用弹性地基梁模型首先研究了钢轨的动应力问题,Fryba[19]对该模型的发展进行了回顾分析,此经典方法在今天被广泛应用。这一最早用于轨道垂向振动分析的连续弹性支承无限长梁模型如图1中轨道模型所示。考虑轨枕和道床参振作用,可建立图4所示连续弹性支承三层叠合梁模型[18]。为了研究道床深度方向各层道砟的振动差异,可进一步建立四层或五层叠合梁模型。

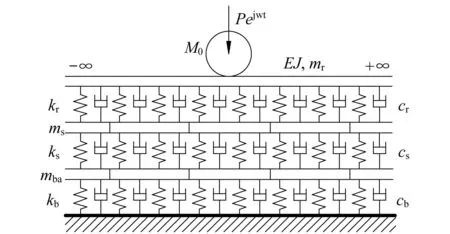
图4　连续弹性支承三层叠合梁模型[18]Fig.4　Three layers-beam model with continuouselastic support [18]

显然,将轨道简化为连续弹性支承梁难以满足钢轨间断支承于轨枕上这一事实,因此发展了轨道垂向振动分析中的连续弹性点支承梁模型,根据模型中是否考虑轨枕及道床的参振,连续弹性点支承梁模型亦可分为单层、双层及三层。其中,三层弹性点支承梁模型如图5所示[18]。

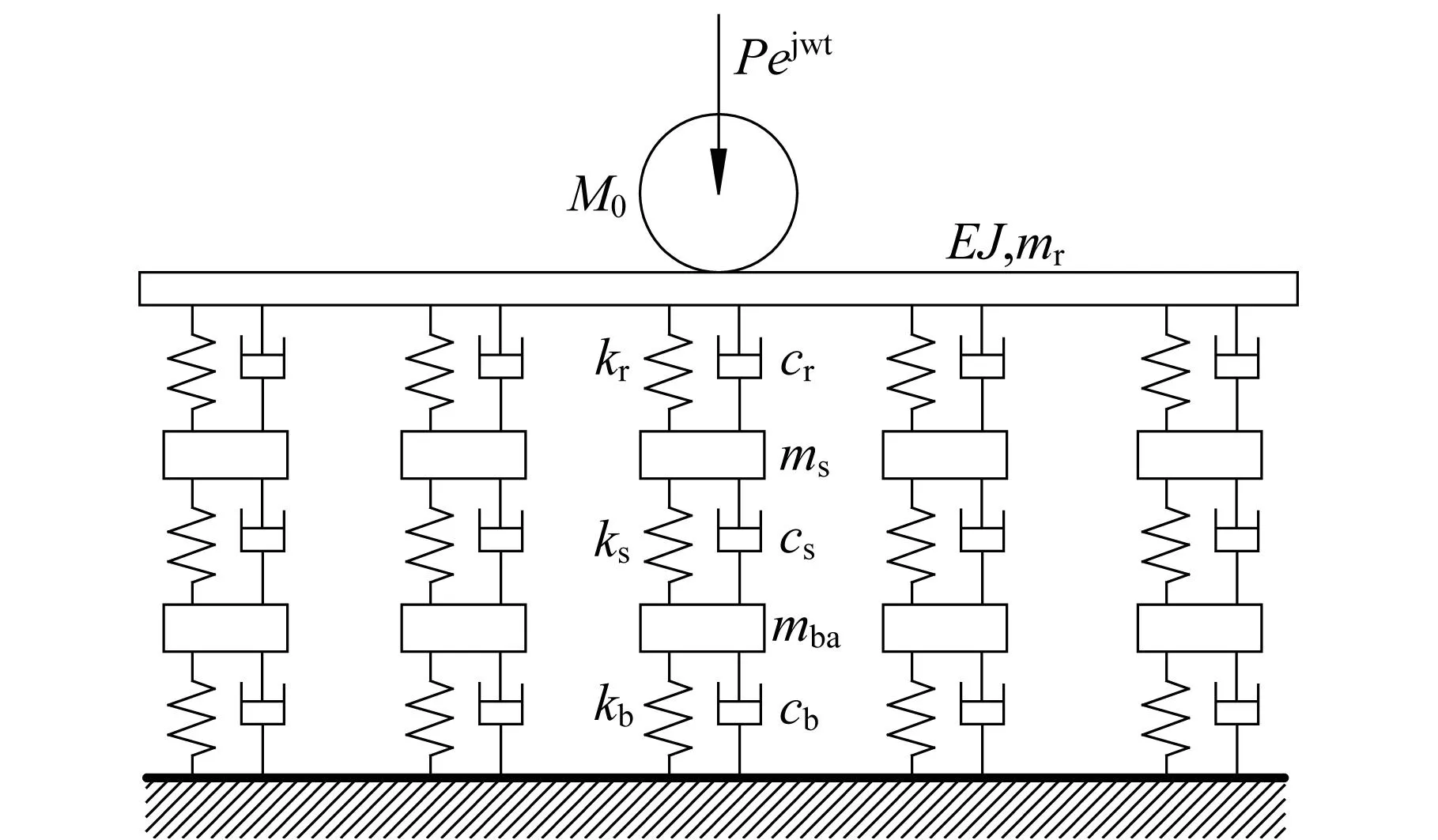
图5　三层弹性点支承模型[18]Fig.5　Three layers model with elastic point support [18]

文献[20]讨论了无砟轨道的建模方法,图6—图8分别介绍了长枕埋入式无砟轨道模型、弹性支承块式无砟轨道模型以及板式无砟轨道模型。

图6　长枕埋入式无砟轨道模型[20]Fig.6　Ballastless track model with embedded long sleepers[20]

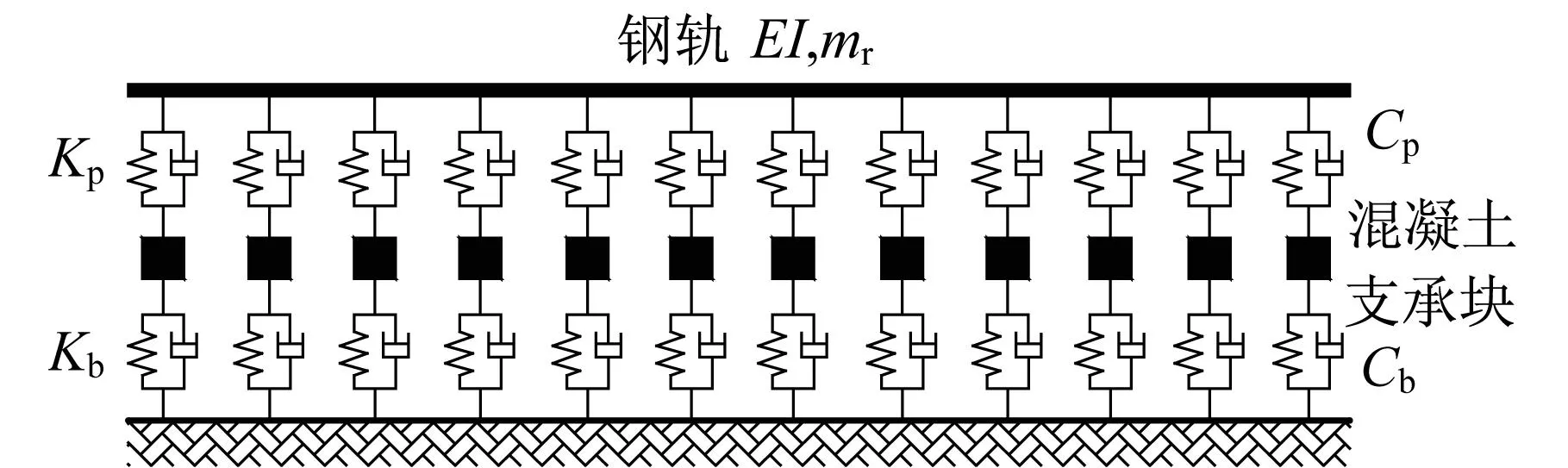
图7　弹性支承块式无砟轨道模型[20]Fig.7　Ballastless track model with elastic bearing blocks [20]

2.3　车辆模型

机车车辆与轨道的耦合作用对轮轨动力效应的影响显著,对车辆模型的大幅简化虽能减少工作量,但难免导致分析误差。因此,车辆的模型也经历由简至繁的过程。最简单的车辆模型将车辆简化为单轮对,且只保留簧下质量而忽略车辆其他部分的影响[18]。此外,可计入簧上质量的影响,如图3中的车辆模型所示。

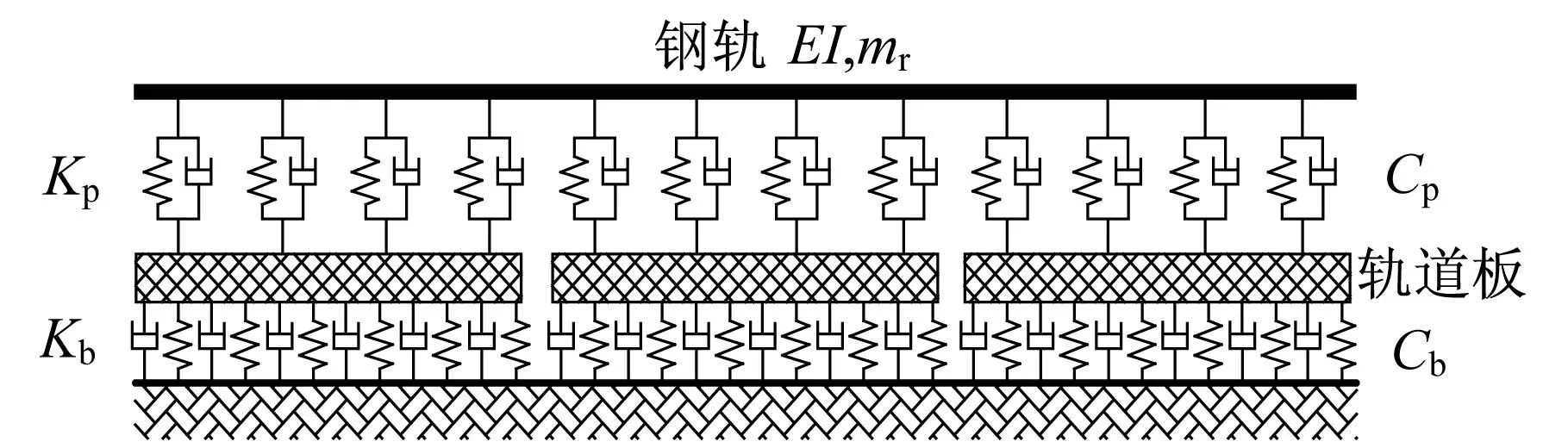
图8　板式无砟轨道[20]Fig.8　Slab-type ballastless track model[20]

1991年,Kisilowski和Knothe分析了车辆相邻轮对之间的动力耦合关系(图9),结果表明,临轮对本位轮处轨道位移的影响较大,且相互动力作用十分明显,将车辆简化为单轮对模型是不甚合理的;1993年,翟婉明等[21]指出,脉冲激扰所引起的轨道高频振动以激振点前后三跨轨枕范围内最为显著,这一距离接近于转向架的固定轴距;1994年,翟婉明、王其昌[22]通过数值分析证明,考虑同一转向架二轮对耦合影响后,计算偏差得到明显降低。因此,在单轮对模型上发展了单侧转向架模型及半车模型(图10)。两者区别在于模型中是否考虑车体参振。

图9　研究相邻轮对相互动力影响的模型[20]Fig.9　The model for analysis of adjacent wheelsets interaction[20]

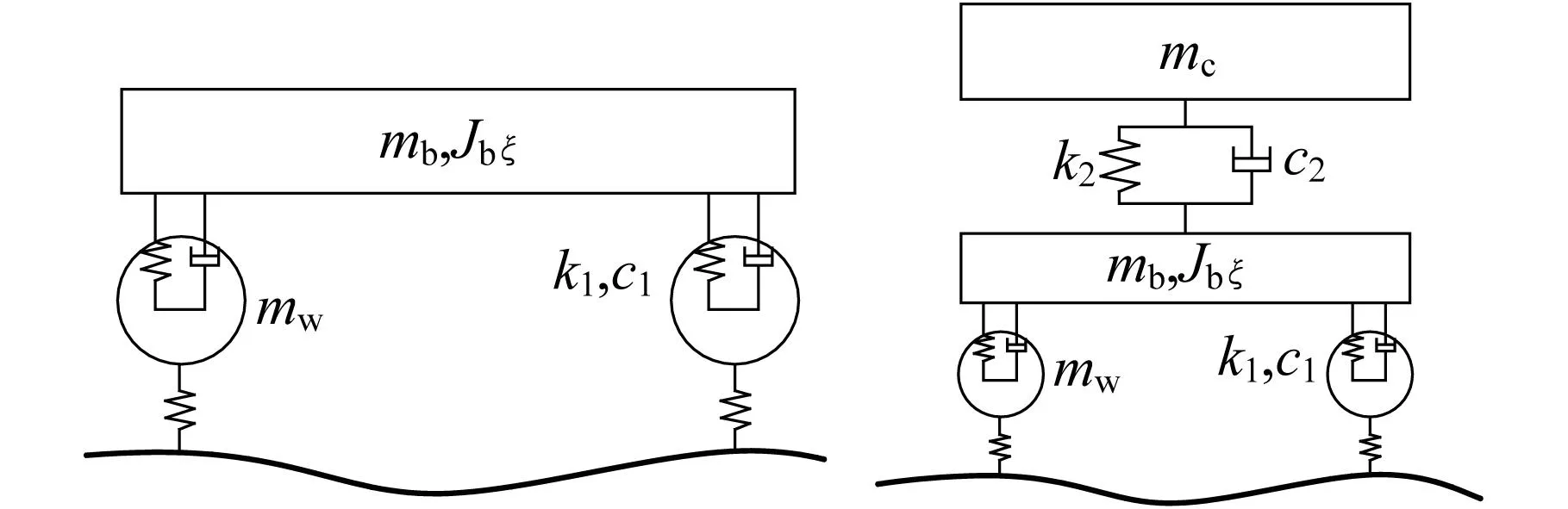
图10　单侧转向架模型(左)及半车模型(右)[18]Fig.10　Bogie model (left) and half vehiclemodel (right) [18]

相比于单侧转向架模型,半车模型在一定程度上考虑了车体低频振动的影响(半车体的垂向振动),但在平面模型中,这种考虑车体作用的影响不明显。文献[22]指出,当轨面存在连续正弦型不平顺时,转向架(半车)模型所得轮轨作用力和道床加速度等数值与整车模型差别较大。因此,发展了整车模型,整车-有砟轨道垂向统一模型如图11所示[20]。

图11　车辆-有砟轨道垂向耦合模型[20]Fig.11　Train-ballast track vertical coupled system[20]

图11中,Mc,Jc为车体质量及其点头惯量;Mt,Jt为前后转向架构架质量及其点头惯量;Mw为各轮对质量;mr,EI为钢轨单位长度质量及钢轨抗弯刚度;Msi为第i号轨枕质量;Mbi为第i号离散道床块质量;Kpz,Cpz为一系悬挂刚度及阻尼;Ksz,Csz为二系悬挂刚度及阻尼;Kpi,Kbi,Kfi,Cpi,Cbi,Cfi分别为每个支撑单元所对应的轨下垫层、道床和路基刚度及阻尼;Kwi,Cwi为离散道床块间剪切刚度及剪切阻尼;Zc,βc为车体沉浮及点头运动位移;Zt1,Zt2,βt1,βt2为前后构架沉浮及点头运动位移;Zw1~Zw4依次为四个轮对垂向振动位移;Z01~Z04依次为轮对对应处轮轨界面位移不平顺;Zr,Zs,Zb为钢轨、轨枕及道床振动位移;Fw(i)(i=1~4)依次为各轮对单侧轮轨力。

2.4　路基参振

高速列车运行过程中,车轮对路基的重复荷载作用频率与路基固有频率较为接近,甚至处于路基固有频率范围内,所以路基的振动问题理应得到重视[18]。尤其是随着软土地区大量高铁的建成与投入运营,其长期服役性能及引起的环境振动问题日益突出,亟需开展系统的基础研究,而软土地区高速荷载作用下路基沉降变形机理十分复杂,国内外对于软土地区高速铁路路基动力问题研究资料较少,研究方法缺乏关联性和体系性,因此,应考虑路基的参振作用,将路基纳入车辆-轨道-路基耦合作用理论模型中,如图12所示。

图12　路基振动分析中的五层叠合梁模型[18]Fig.12　Five layers-beam model for vibrationanalysis of subgrade[18]

图12中,轨道、路基自上而下地分层,依次考虑钢轨、轨枕、道床、路基第一层及路基第二层的参振作用,以求解较低频率下的轨道、路基同相振动的情况。其中,只有钢轨具有抗弯刚度,是实际的抗弯梁,其余各层只有参振质量而无抗弯刚度,即视为“形式上的梁”。

分层叠合梁模型虽然简单,但是对路基的模拟过于简化,与实际情况存在较大误差,因此发展了有限元法进行求解。

然而,在多数情况下,轮轨间的动作用力不可知,无法将动荷载作用在轨道或者路基面上,因此,有必要将路基振动耦合在车辆-轨道-路基大系统中。此时轨枕以下的道床和路基宜采用有限单元方法进行离散处理。为缩短模型的长度,控制道床和路基的自由度数量,减少计算工作量,宜选择半车(或转向架)耦合振动模型,如图13所示[18]。

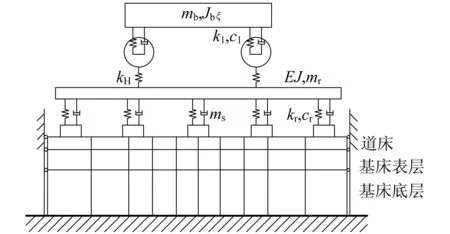
图13　单侧转向架-轨道-路基垂向耦合振动平面模型[18]Fig.13　Vertical vibration model of bogie-track-subgradecoupled system [18]

根据求解问题的需要,无砟轨道的路基模型亦有多种形式,较为典型的是叠合梁模型[23](图14)和有限单元模型[24](图15)。

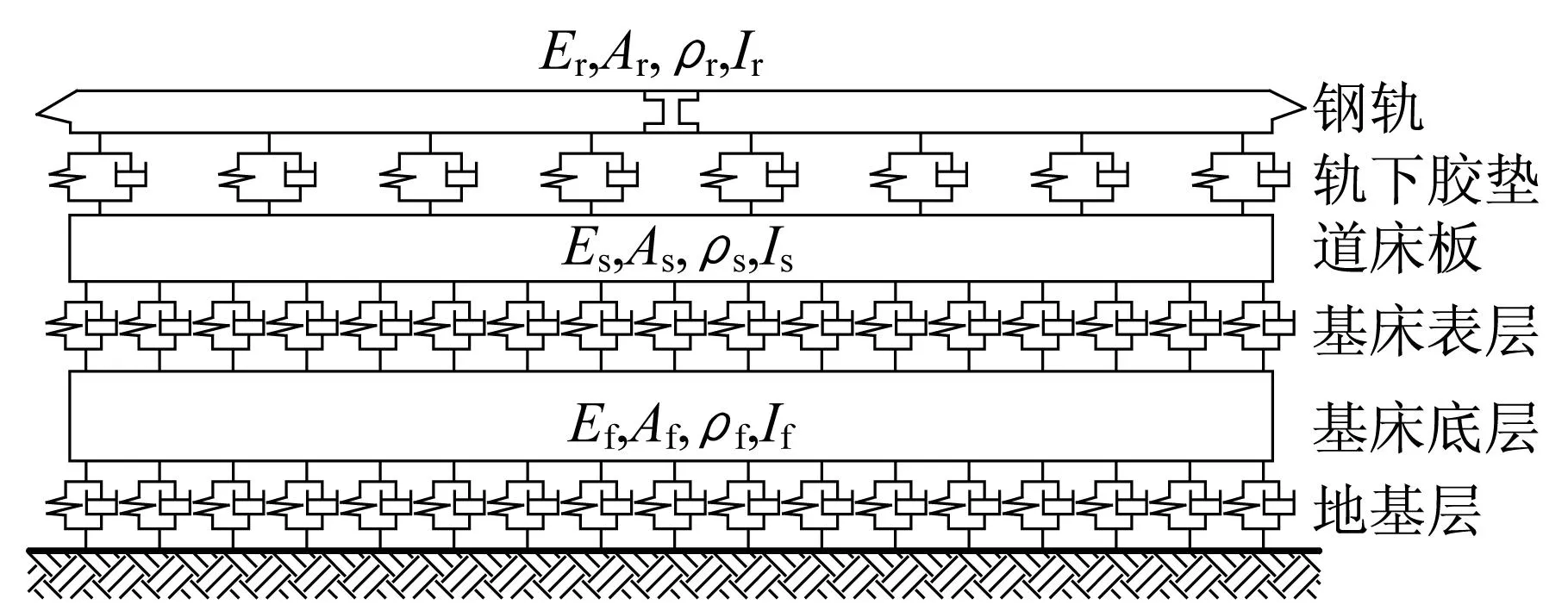
图14　双块式无砟轨道-路基耦合动力学模型[23]Fig.14　Dynamic model of coupled double-block ballastlesstrack and subgrade system[23]

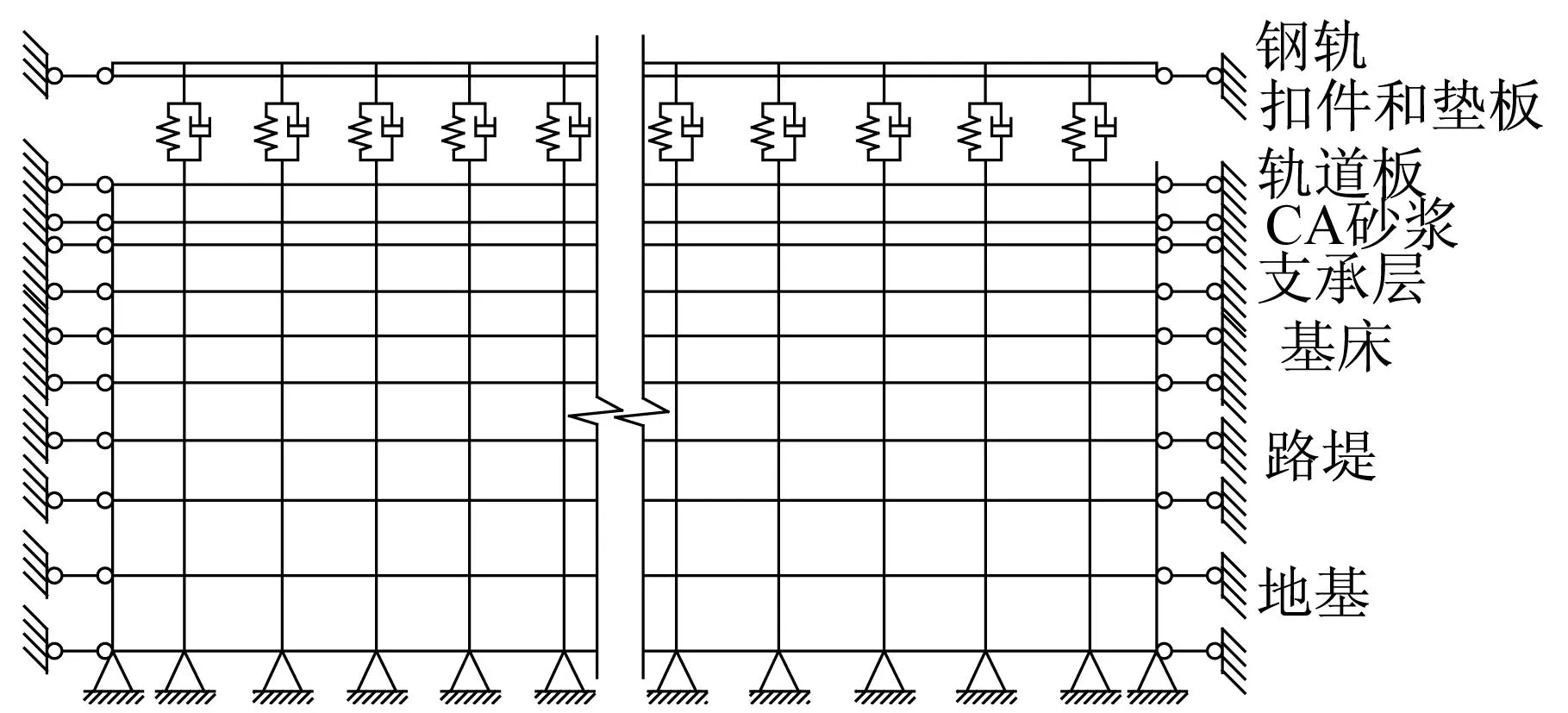
图15　板式轨道-路基垂向耦合动力模型[24]Fig.15　Finite element model of slab track and subgrade[24]

图14中,钢轨视为连续弹性离散点支承基础上的无限长Timoshenko梁,具有垂向和截面转角运动自由度;双块式轨枕、道床和支承层视为一个整体,统称为道床板,用两端自由的Euler梁来模拟,具有垂向运动自由度;轨枕与钢轨之间在垂向用线性弹簧和黏性阻尼联结;基床表层由沥青混凝土组成,视为有一定弹性的垫层,用线性弹簧和黏性阻尼来模拟;基床底层被视为无限长Euler梁,只具有垂向运动自由度;地基层用线性弹簧和黏性阻尼来模拟。

图15中,钢轨离散成梁单元;垫板和扣件采用弹簧-阻尼单元模拟;轨道板、水泥乳化沥青砂浆层、支承层及以下介质包括路基均离散成四边形单元。

随着计算机技术的飞速发展和国家经济实力的大幅提升,数值模拟和试验得到强有力的保障,使车辆-轨道-路基耦合作用理论得到发展和验证。下面对车辆-轨道-路基垂向耦合模型的发展现状进行介绍。

3车辆-轨道-路基垂向耦合模型发展现状

3.1　模型实际应用

随着车辆-轨道-路基垂向耦合模型的成熟,以模型解决实际问题的研究工作得到迅速发展。

1999年,翟婉明等[25]通过建立高速车辆-板式轨道垂向相互作用模型,研究高速铁路板式轨道动力特性,分析结果表明,轨道竖错不平顺影响板式轨道变形与承载强度,CA砂浆垫层弹性模量的合理取值范围是1000~1500MN/m3,且阻尼取大值将有利于降低板式轨道结构振动。

2000年,梁波等[26]将轨道-路基作为参振子结构纳入车辆计算模型,建立了车辆-路基系统的垂向耦合动力分析模型,从系统的观念和体系匹配的角度研究了路基尤其是高速铁路路基设计参数与车辆运行品质的相互关系。

2001年,毛利军、雷晓燕[27]建立整车-有砟轨道模型,对考虑轨面高低随机不平顺的线路,在频域和时域内进行了车辆、轨道系统随机振动分析,探讨了不同工况下系统高、低频振动特性。

2002年,练松良、刘富[28]建立了整车-轨道模型,对英国Derby铁路研究中心提出的P1和P2力计算公式进行对比验证,研究列车通过钢轨接头时轨道刚度变化对轮轨冲击荷载的动力影响,建议轨道结构采用弹性设计思想;Sun和Dhanasekar[29]也建立了整车-有砟轨道耦合模型,其中,车辆子系统采用10自由度模型,轨道细化为包括道砟和底砟的4层离散支承模型,对车辆及轨道优化设计提供基础。

2008年,冯青松等[30]建立了移动车辆-连续弹性3层梁轨道垂向耦合振动模型,研究了列车速度、轨道不平顺以及轨下基础刚度对轨道振动的影响。

2010年,Xia等[31]根据车辆动力学、轨道动力学及路基的格林函数建立了耦合模型,实例求解结果表明:列车速度、路基土特性明显影响地面振动且轨面不平顺会影响地面振动的高频成分。

2011年,张健等[32]通过垂向半车-轨道耦合动力学模型,分析了采用解析方法的模态叠加法、有限元法的模态叠加法和有限元法的直接积分法求解车辆-轨道耦合动力学钢轨模型的计算精度与计算效率,其中,分别选用Bernoulli-Euler梁和Rayleigh-Timoshenko梁模拟钢轨。

2012年,李新[33]用有限元法建立了列车-无砟轨道-路基系统垂向振动模型,采用移动连接单元在单元层面上实现了列车与轨道之间的耦合关系,大大简化了系统的动力学建模。模型的数值仿真计算结果表明模型中钢轨动位移受轨下结构参数的影响较大,最大峰值偏差可达40%。

2013年,赵乾峰等[34]采用统一模型法,建立车辆、钢轨、轨枕、道床和路基为一体的二系垂向耦合动力分析模型,利用新型显式积分法进行数值积分计算,分析了列车速度、轨枕间距、轨道不平顺及列车重量对列车运行的品质、动位移以及轨道结构振动的影响规律;Ma等[35]建立车辆-轨道-路基垂向耦合模型,论证该模型解决车辆-轨道-路基耦合振动问题的可靠性,并可为相关设计参数提供理论基础。

2014年,杨新文等[23]建立车辆-双块式无砟轨道-路基垂向耦合动力学分析模型,从频域角度推导双块式无砟轨道和路基系统振动响应的解析表达式,计算得出轨道和路基耦合系统的动柔度特性,结合虚拟激励法提出该模型在轨道随机不平顺激励时动力学响应的求解方法,分析高速列车荷载作用下双块式无砟轨道和路基的随机振动响应及其振动传递特性;Tran等[36]利用移动单元法建立车辆-轨道模型,提出移动单元广义质量矩阵、阻尼矩阵及刚度矩阵的计算方程,研究线性与非线性轮轨接触条件下不同参数对轮轨接触力放大系数的影响,重点研究轨头表面粗糙度与轮载对“跳轮”现象发生的影响。

3.2　模型与有限元软件结合及试验验证

随着计算机有限元软件运算能力的提高以及试验技术的成熟,车辆-轨道-路基垂向耦合模型与有限元软件的联合应用及试验验证,使得高铁线路振动问题的求解更加方便、可靠。

1996年,翟婉明等[37]以历次主要的轮轨动力学现场试验为基础,对所建立的车辆-轨道相互作用统一模型及其计算机仿真分析软件VICT进行了全面系统的试验验证,结果表明,耦合模型正确可靠。

2003年,翟婉明等[38]在铁路线路上对道床振动进行了现场实测,试验结果与理论分析结果相吻合,从而验证了在道床振动分析模型中引入道床剪切刚度和剪切阻尼的正确有效性。

2008年,金亮星和乔世范[39]根据秦-沈客运专线车辆的结构形式、悬挂特性及轨道结构特点,建立了具有两系悬挂的车辆-轨道-路基垂向统一模型,对轨道随机不平顺激励下系统的响应进行了数值计算,将数值模拟结果与现场试验实测数据对比,结果表明,该模型能较真实地反映耦合系统垂向相互作用的基本力学特性。

2009年,马学宁等[40]建立有砟轨道的垂向耦合动力分析模型,分析列车速度变化对车辆运行品质、动位移以及路基动应力的影响,通过垂向耦合动力模型计算得到轮轨相互作用力,将此力作为三维轨道-路基有限元软件模型的激励,进而求得路基动应力随车辆速度变化的影响。

2011年,马学宁等[24]建立无砟轨道的垂向耦合动力分析模型,与文献[40]相同,利用模型所得到的轮轨作用力作为板式轨道-路基结构的瞬态分析输入,利用三维动力有限元法,分析不同参数下路基的动力响应,结果表明,路基动应力随速度的提高幅度及基床加速度小于有砟轨道相应值,表明无砟轨道有效改善列车荷载对路基基床的振动作用。

2012年,翟婉明,韩海燕[41]将列车引起的地面振动问题拆分成两个子问题进行研究:首先建立列车-板式无砟轨道叠合梁垂向耦合模型,分析车辆与轨道之间动态相互作用,获得作用于轨道结构上的激振力;然后借助于ANSYS有限元软件建立轨道-土体有限元模型,分析列车动荷载作用下土体的振动特性。

4车辆-轨道-路基垂向耦合模型发展趋势及展望

4.1　发展趋势

从1825年世界上出现第一条铁路后的漫长时间里,车辆-轨道-路基系统的理论研究经过了一段艰苦的过程。从1926年Timoshenko发表此领域的第一篇论文至今,铁路系统振动动力研究得到了长足发展,其基本发展趋势可以总结为:

(1) 轨道模型、车辆模型及路基模型不断完善,取得了由简至繁、由粗至精的进步。

(2) 轨道模型、车辆模型及路基模型在发展的过程中互相融合,使得车辆-轨道-路基耦合作用模型丰富多样,适合解决不同的实际问题。

(3) 我国有关高速铁路动力学问题的研究已基本采用耦合动力学的方法,而不再是传统的孤立系统动力学分析方法。

(4) 计算机有限元软件和试验条件的发展对车辆-轨道-路基耦合模型应用的合理性、准确性提供了有力的保障,振动问题的解决也趋向于多手段、多途径。

4.2　展　望

(1) 计算机软件的应用对高速铁路振动问题的求解提供了方便,但是目前的研究多局限于利用有限元软件建立轨道-路基模型,轨上荷载多采用经验公式的结果或者由车辆-轨道模型得出的轮轨力间接施加在模型上,为了使有限元软件更好地反映轮轨相互作用并与理论模型结果对比,在三维有限元软件中建立完整的车辆模型势在必行。

(2) 虽然整车模型具有最全面的计算分析功能而被广泛采用,但考虑到轮载的叠加效应主要集中在两个相邻车厢的相邻转向架的各轮对之间,同一车厢两转向架之间的叠加效应较小[42],所以有必要在理论模型中考虑前后车厢的叠加作用;然而在模型中建立整个列车模型势必增加模型长度,对求解造成额外的巨大计算量,因此,若非确有必要,如研究长波长轨道不平顺问题,宜在“半车”模型的基础上建立如图16所示的“两半车”模型。

“两半车”模型可以在不显著增加轨道长度的情况下,考虑两个相邻车厢的相邻转向架各轮对之间轮载的叠加效应,并能适当考虑车辆连接装置对车辆垂向振动的影响。

5结语

随着我国铁路“多拉快跑”的发展趋势,高速铁路的发展势如破竹。为解决高速铁路振动这一复杂、大系统、动态相互作用问题,应将车辆系统、轨道系统及路基系统作为一个相互作用、相互依存的整体大系统加以考察。

目前,已有丰富多样的车辆-轨道-路基耦合作用模型,根据求解问题的不同,可以选择不同的模型,甚至提出新的合适模型。

有限元软件的发展及试验条件的成熟,为高速铁路振动问题的求解提供了支持和保障,综合应用理论模型、数值模拟及试验验证等手段解决高速铁路振动问题,保证高速铁路运行安全值得所有高速铁路研究人员和技术人员共同努力。

参考文献

[1]严隽耄,傅茂海.车辆工程[M].3版.北京:中国铁道出版社,2007.

Yan Juanmao,Fu Maohai.Vehicle engineering [M].3rd ed.Beijing:China Railway Publishing House,2007.(in Chinese)

[2]Garg V K,Dukkipati R V.Dynamics of railway vehicle systems[M].Toronto:Academic Press,1984.

[3]詹斐生.机车动力学[M].北京:中国铁道出版社,1990.

Zhan Feisheng.Locomotive dynamics[M].Beijing:China Railway Publishing House,1990.(in Chinese)

[4]王福天.车辆系统动力学[M].北京:中国铁道出版社,1994.

Wang Futian.Vehicle system dynamics[M].Beijing:China Railway Publishing House,1994.(in Chinese)

[5]Knothe K.Gleisdynamik[J].Stahlbau,2001,70(9):733-734.

[6]左藤裕.轨道力学[M].卢肇英,译.北京:中国铁道出版社,1981.

Zuo Tengyu.Track mechanics[M].Transl:Lu Zhao-ying.Beijing:China Railway Publishing House,1981.(in Chinese)

[7]练松良.轨道动力学[M].上海:同济大学出版社,2003.

Lian Songliang.Track dynamics[M].Shanghai:Tongji University Press,2003.(in Chinese)

[8]边学成,陈云敏.列车荷载作用下轨道和地基的动响应分析[J].力学学报,2005,37(4):477-484.

Bian Xuecheng,Chen Yunmin.Dynamic analysis of track and ground coupled system with high-speed train loads[J].Chinese Journal of Theoretical and Applied Mechanics,2005,37(4):477-484.(in Chinese)

[9]Kaynia A M,Madshus C,Zackrission P.Ground vibration from high-speed trains:prediction and countermeasure[J].Journal of Geotechnical and Geo-environmental Engineering,2000,126(6):531-537.

[10]Takemiya H,Bian X C.Substructure simulation of inhomogeneous track and layered ground dynamics interaction under train passage[J].Journal of Engineering Mechanics-ASCE,2005,131(7):699-711.

[11]Bian Xuecheng,Jiang Hongguang,Chen Yunmin.Accumulative deformation in railway track induced by high-speed traffic loading of the trains[J].Earthquake Engineering and Engineering Vibration,2010,9(3):319-326.

[12]Jenkins H H.The effect of track and vehicle parameters on wheel/rail vertical dynamic forces[J].Railway Engineering Journal,1974,3(1):2-16.

[13]Newton S G,Clark R A.An investigation into the dynamic effects on the track of wheel flats on railway vehicles[J].Journal of Mechanical Engineering Science,1979,21(4):287-297.

[14]Sato Y.Abnormal wheel load of test train[J].Permanent Way,1973,14:1-8.

[15]吴章江,王浦强,李湘敏,等.车辆通过轨道低扣接头的垂向轮轨作用力计算[J].铁道机车车辆,1982(1):24-30.

Wu Zhangjiang,Wang Puqiang,Li Xiangmin,et al.Calculation of vertical wheel/rail force while driving through the lower rail joint[J].Railway Locomotive and Car,1982(1):24-30.(in Chinese)

[16]李定清.轮轨垂直相互动力作用及其动力响应[J].铁道学报,1987,9(1):1-8.

Li Dingqing.Wheel/track vertical dynamic action and responses[J].Journal of the China Railway Society,1987,9(1):1-8.(in Chinese)

[17]许实儒,徐维杰,仲延禧.钢轨接头处轮轨冲击力的模拟分析[J].铁道学报,1989,(S1):99-109.

Xu Shiru,Xu Weijie,Zhong Yanxi.A simulation analysis of wheel/rail impact force at the rail joint[J].Journal of the China Railway Society,1989(S1):99-109.(in Chinese)

[18]刘学毅,王平.车辆-轨道-路基系统动力学[M].成都:西南交通大学出版社,2010.

Liu Xueyi,Wang Ping.Vehicle-track-subgrade system dynamics[M].Chengdu:Southwest Jiao Tong University Press,2010.(in Chinese)

[19]Fryba L.History of winkler foundation[J].Vehicle System Dynamics,1995,24(S):7-12.

[20]翟婉明.车辆-轨道耦合动力学[M].3版.北京:科学出版社,2007.

Zhai Wanming.Vehicle-track coupling dynamics[M].3rd Ed.Beijing:Science Press,2007.(in Chinese)

[21]翟婉明,孙翔,詹斐生.机车车辆与轨道垂向相互作用的计算机仿真研究[J].中国铁道科学,1993,14(1):42-50.

Zhai Wanming,Sun Xiang,Zhan Feisheng.Computer simulation of the vertical dynamic interactions between track and trains[J].China Railway Science,1993,14(1):42-50.(in Chinese)

[22]翟婉明,王其昌.轮轨动力分析模型研究[J].铁道学报,1994,16(1):64-72.

Zhai Wanming,Wang Qichang.A study on the analytical models for wheel/rail dynamics[J].Journal of the China Railway Society,1994,16(1):64-72.(in Chinese)

[23]杨新文,宫全美,周顺华,等.高速列车作用下双块式无砟轨道与路基垂向耦合振动分析[J].铁道学报,2014,36(8):75-83.

Yang Xinwen,Gong Quanmei,Zhou Shunhua,et al.Analysis on vertical vibration of coupled double-block ballastless track and subgrade system under high-speed train running[J].Journal of the China Railway Society,2014,36(8):75-83.(in Chinese)

[24]马学宁,梁波,高峰.高速铁路板式无砟轨道-路基结构动力特性研究[J].铁道学报,2011,33(2):72-78.

Ma Xuening,Liang Bo,Gao Feng.Study on the dynamic properties of slab ballastless track and subgrade structure on high-speed railway[J].Journal of the China Railway Society,2011,33(2):72-78.(in Chinese)

[25]翟婉明,韩卫军,蔡成标,等.高速铁路板式轨道动力特性研究[J].铁道学报,1999,21(6):65-69.

Zhai Wanming,Han Weijun,Cai Chengbiao,et al.Dynamic properties of high-speed railway slab tracks[J].Journal of the China Railway Society,1999,21(6):65-69.(in Chinese)

[26]梁波,蔡英,朱东生.车-路垂向耦合系统的动力分析[J].铁道学报,2000,22(5):65-71.

Liang Bo,Cai Ying,Zhu Dongsheng.Dynamic analysis on vehicle-subgrade model of vertical coupled system[J].Journal of the China Railway Society,2000,22(5):65-71.(in Chinese)

[27]毛利军,雷晓燕.车辆-轨道耦合系统随机振动分析[J].华东交通大学学报,2001,18(2):6-12.

Mao Lijun,Lei Xiaoyan.An analysis of random vibration of vehicle/ track coupling system[J].Journal of East China Jiao-tong University,2001,18(2):6-12.(in Chinese)

[28]练松良,刘富.轨道刚度变化对轮轨冲击荷载的动力影响[J].同济大学学报,2002,30(4):427-430.

Lian Songliang,Liu Fu.Effect of track stiffness uneven on wheel/rail impact load[J].Journal of Tongji University,2002,30(4):427-430.(in Chinese)

[29]Sun Y Q,Dhanasekar M.A dynamic model for the vertical interaction of the rail track and wagon system[J].International Journal of Solids and Structures,2002,39(5):1337-1359.

[30]冯青松,雷晓燕,练松良.不平顺条件下高速铁路轨道振动的解析研究[J].振动工程学报,2008,21(6):559-564.

Feng Qingsong,Lei Xiaoyan,Lian Songliang.Vibration analysis of high-speed railway tracks with geometric irregularities[J].Journal of Vibration Engineering,2008,21(6):559-564.(in Chinese)

[31]Xia H,Cao Y M,De Roeck G.Theoretical modeling and characteristic analysis of moving-train induced ground vibrations[J].Journal of Sound and Vibration,2010,329(7):819-832.

[32]张健,金学松,肖新标,等.车辆-轨道耦合动力学钢轨模型求解方法[J].交通运输工程学报,2011,11(2):32-38.

Zhang Jian,Jin Xuesong,Xiao Xinbiao,et al.Solution methods of rail model in vehicle-track coupling dynamics[J].Journal of Traffic and Transportation Engineering,2011,11(2):32-38.(in Chinese)

[33]李新.高速铁路无砟轨道-路基系统耦合振动研究[D].长沙:中南大学,2012.

Li Xin.Study on the coupling vibration of high-speed railway ballastless track-subgrade system[D].Changsha:Central South University,2012.(in Chinese)

[34]赵乾峰,姚林泉,张辉.高速列车-轨道-路基耦合垂向振动特性分析[J].力学季刊,2013,34(1):16-24.

Zhao Qianfeng,Yao Linquan,Zhang Hui.Analysis of vertical vibration property of high-speed train-track-subgrade coupled[J].Chinese Quarterly of Mechanics,2013,34(1):16-24.(in Chinese)

[35]Ma X N,Wang X,Liang B,et al.Dynamic model of subgrade using a coupled vehicle-track-subgrade method[C].IACGE 2013:Challenges and recent advances in geotechnical and seismic research and practices.America:American Society of Civil Engineers,2013,334-342.

[36]Tran M T,Ang K K,Luong V H.Vertical dynamic response of non-uniform motion of high-speed rails[J].Journal of Sound and Vibration,2014,333(21):5427-5442.

[37]翟婉明,蔡成标,史炎,等.车辆-轨道相互作用统一模型及软件的试验验证[J].铁道学报,1996,18(4):42-46.

Zhai Wanming,Cai Chengbiao,Shi Yan,et al.Experimental verification of a unified vehicle/track interaction model[J].Journal of the China Railway Society,1996,18(4):42-46.(in Chinese)

[38]翟婉明,林建辉,王开云.铁路道床振动的理论模拟与试验研究[J].振动工程学报,2003,16(4):404-408.

Zhai Wanming,Lin Jianhui,Wang Kaiyun.Theoretical simulation and field experiment on vibration of railway ballast[J].Journal of Vibration Engineering,2003,16(4):404-408.(in Chinese)

[39]金亮星,乔世范.车辆-轨道-路基系统垂向动力分析模型的试验验证[J].振动与冲击,2008,27(3):38-41.

Jin Liangxing,Qiao Shifan.Test verification of vertical dynamic analysis model of vehicle track-subgrade system[J].Journal of Vibration and Shock,2008,27(3):38-41.(in Chinese)

[40]马学宁,梁波,高峰.列车速度对车辆-轨道-路基系统动力特性的影响[J].中国铁道科学,2009,30(2):7-13.

Ma Xuening,Liang Bo,Gao Feng.Influence of vehicle speed on the dynamic characteristics of vehicle track-subgrade system[J].China Railway Science,2009,30(2):7-13.(in Chinese)

[41]翟婉明,韩海燕.高速列车运行于软土地基线路引起的地面振动研究[J].中国科学,2012,42(10):1148-1156.

Zhai Wanming,Han Haiyan.Study on ground vibration caused by high-speed train travelling on soft foundation[J].Science China Press,2012,42(10):1148- 1156.(in Chinese)

[42]王启云,张家生,孟飞,等.高速铁路轨道路基模型及动力加载研究[J].铁道学报,2012,34(12):90-95.

Wang Qiyun,Zhang Jiasheng,Meng Fei,et al.Study on track-subgrade model of high-speed railway and dynamical loading[J].Journal of the China Railway Society,2012,34(12):90-95.(in Chinese)

基金项目：国家重点基础研究发展计划项目(2014CB049100)；国家自然科学基金项目(51322803)

收稿日期：2015-10-10

*联系作者， Email: yingzhou@tongji.edu.cn