考虑非设计工况的螺旋桨优化设计方法

常欣，孙帅，王超，莫涛

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

考虑非设计工况的螺旋桨优化设计方法

常欣，孙帅，王超，莫涛

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

摘要：为提高螺旋桨的性能，研究了考虑非设计工况时螺旋桨效率的优化设计方法。以母型桨设计进速周围多个进速点对应的敞水效率为目标函数，以螺距比的径向分布为优化变量，以推力、扭矩和空泡性能为约束条件建立优化数学模型。通过对不同工况的效率值设置权重并进行加权求和的方法，将多目标优化模型转变为单目标优化模型，利用面元法求解螺旋桨的水动力性能，应用柏利尔商船限界线表达空泡性能，基于简单遗传算法对模型进行求解，得到了优化后的螺旋桨螺距比的径向分布，将考虑非设计工况与考虑设计工况下的优化结果进行了对比。对比结果表明，由于船舶航行时航速的变化，仅考虑设计工况下进行螺旋桨优化往往达不到预期的节能效果，需要综合考虑设计航速周围多个工况点对应的效率。

关键词：螺旋桨优化；优化设计；非设计工况；权重；简单遗传算法；螺距比分布；敞水效率

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20151106.1047.002.html

孙帅(1989-), 男,博士研究生.

船舶高效螺旋桨的设计一直是船舶水动力学的重点研究问题。目前以高效节能为目标的船舶螺旋桨的设计与优化通常是针对设计航速下的效率最大化来进行的，设计者结合现有成熟理论或优化算法考虑螺旋桨的一个要素或是多个要素对螺旋桨进行优化设计，如螺距分布的优化、拱度优化、侧斜优化、纵倾的优化、桨叶剖面形状优化[1-6]等。

但是实践表明，单纯考虑设计航速下的螺旋桨效率最大化而设计出的螺旋桨在实际运营过程中往往达不到预期的效果。这是因为船舶实际运营过程中由于风、浪、流的存在以及船舶排水量的变化，船舶螺旋桨的进速系数无法始终维持在设计工况上，实际进速系数往往是在设计进速周围波动的。因此，对螺旋桨作进一步的优化设计是十分必要的。这就需要考虑螺旋桨效率在一定的设计进速系数波动范围内的最佳化，并以此为优化目标函数对螺旋桨进行优化设计。设计进速的波动范围内对应着多个离散的螺旋桨敞水效率值，要寻求该范围内效率的最优化，即是搜索使得这些效率值同时最优的解，这是一个考虑多工况的优化问题。

本文探讨了简单遗传算法结合加权求和方法对该类问题的分析处理过程，初步建立一种考虑螺旋桨非设计工况点效率的螺旋桨优化设计方法。

1螺旋桨优化数学模型

1.1　优化目标函数

图1表示某母型桨的敞水效率曲线，其最佳效率对应的进速系数为J0，传统的以螺旋桨敞水效率为优化目标的螺旋桨优化设计中，是以J=J0时，所对应的螺旋桨敞水效率为优化目标函数的。

图1　螺旋桨敞水效率曲线Fig.1　Open water efficiency of propeller

(1)

1.2　优化设计变量

(2)

式中：d/D表示毂径比，将螺距比分布范围转化为0~1；xk在x∈(d/D,1.0)间均匀选取。对于一条螺距径向分布曲线可取k=6。优化变量为螺距比分布曲线的6个控制参数a1,a2,…,a6。

螺旋桨优化的约束条件为需要满足螺旋桨的空泡性能和强度要求，强度的控制只需保证桨叶厚度不低于母型桨即可，对于螺旋桨空泡性能的预报利用柏利尔商船限界线[7]。

因此，螺旋桨优化设计的数学模型可表示为

(3)

1.3　约束条件

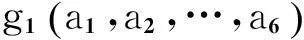
2确定目标函数

图2　实船航速变化曲线Fig.2　The full-scale ship speed

式(1)确定的N个进速系数Ji,i=1,2,…,N，对应N个航速Vri,i=1,2，…,N。将集合

均分为N个子集ri,i=1,2,…,N，那么显然有每个子集ri的中点就是与Ji对应的航速Vri，即有式(4)成立。

(4)

特别的有r1的中点是VA，rN的中点是VB，rN+1/2的中点是V0。如图3所示。

图3　航速变化累积分布函数的确定Fig.3　The determination of speed change cumulative distribution function

(5)

(6)

因此，对于由式(3)确定的优化模型，采用加权求和方法处理多目标优化问题时，权重ωi的取值为

(7)

根据式(5)显然有

(8)

则优化目标函数为

(9)

(10)

3优化方法

在确定了目标函数、优化变量以及约束条件后，选择简单遗传算法(SGA)来进行优化计算，关于SGA的具体流程这里不详细描述，请参考文献[8]。螺旋桨的性能通过面元法来进行计算[9-10]。

(11)

图4　螺旋桨优化设计流程Fig.4　The design process of propeller optimization

4优化算例与结果分析

4.1　优化算例

表1　初始螺距比分布方案

多目标的确定中取J0=0.86为设计进速点，领域半径Δ=0.05，则JA=0.81，JB=0.91。船舶实际运营过程中由于风、浪、流等因素导致的船舶航速的变化较小，因此认为Δ=0.05是合理的。取目标函数个数N=5。则算例中的5个目标函数为

(12)

由表2可知子集区间中点对应的进速系数即是本算例中5个目标函数的计算进速系数值。又知正态分布密度函数为

表2　子集的划分Table 2　The partition of subset

根据标准正态分布表，可得区间累积分布值如表3所示。根据表3可以求取航速变化分布概率，如表4所示。则最终该算例中5个目标函数的对应权重的取值如表5所示。目标函数最终可以表示为

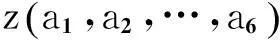
0.576 2f3+0.203 7f4+0.008 2f5

(13)

表3　区间累积分布值Table 3　Interval cumulative distribution value

表4　航速变化分布概率Table 4　The probability distribution of the change speed

表5　权重取值Table 5　The weights

4.2　结果分析

根据式(13)求出目标函数值并确定了初始螺距分布曲线后，即可按照图4的优化流程进行优化。遗传优化目标函数变化如图5所示。

图5　目标函数变化曲线Fig.5　Variation curves of objective function

优化前后桨叶螺距比径向分布曲线如图6所示。螺距比径向分布初始值是Hicks-Henne形函数方法的母型螺距比分布曲线，目的是为了保证优化螺距比径向分布曲线的单调性。与最终结果的对比发现，优化后的螺距比径向分布曲线总体保持单调递减，在桨叶叶根处和叶梢处变化率比桨叶中部大，即桨叶中部螺距比变化相对平缓。

表6给出了原桨敞水效率的单目标优化和多目标优化设计结果。可以看出在J=0.86时，敞水效率都得到了提升，单目标相对原桨提高了1.25%，加权求和方法则提升了1.21%。如果考虑设计进速系数点周围多个敞水效率的加权求和，那么原桨的加权和为0.721 79，单目标优化的加权和为0.726 28，而多目标优化的加权和为0.728 91。 单目标优化提高了0.62%，而多目标优化则提高了0.986%。

图6　优化前后螺距比径向分布Fig.6　The radial distribution of the pitch ratio before and after optimizing

表6　不同进速系数下敞水效率对比Table 6　The comparison of open water efficiency under different advance coefficients

5结论

文章基于简单遗传算法结合加权求和方法，将多目标优化模型转化为单目标优化模型，以螺旋桨设计工况点附近范围内的效率加权和为优化目标，以螺距比径向分布为优化变量，以推力和空泡性能为约束条件，建立了一种考虑螺旋桨非设计工况点效率的螺旋桨优化设计方法。以AU5-65图谱桨为原型桨进行了优化设计。将优化后的结果与原桨以及以设计航速点的效率为目标进行优化后的结果进行了对比，结果表明：

1)无论是只考虑设计工况点的效率还是考虑设计工况点附近范围内的效率来进行优化，螺旋桨的效率都较原图谱桨有不同程度的提高，说明图谱设计的螺旋桨性能存在优化的空间；

2)考虑设计工况点附近范围内的效率来进行优化时，权重的取值对优化后的效果起决定性的作用，而权重的取值则依赖于船舶运营过程中航速分布的统计结果；

3)只考虑设计工况点的效率来进行优化，在船舶实际运营过程中其优化效果将明显下降，而考虑设计工况点附近范围内的效率来进行优化的效果要更好。

本文工作是将综合螺旋桨设计工况点附近范围内的效率优化方法应用到螺旋桨设计中的一个尝试，旨在建立一种优化思路和方法，仅选择了螺距比径向分布这一设计变量，优化目标也只选择了效率。下一步需要进一步研究多变量多目标的优化设计问题。

参考文献：

[1]MA Cheng, CAI Haopeng, QIAN Zhengfang, et al. The design of propeller and propeller boss cap fins (PBCF) by an integrative method[J]. Journal of Hydrodynamics, Series B, 2014, 26(4): 586-593.

[2]曾志波, 丁恩宝, 唐登海. 基于BP人工神经网络和遗传算法的船舶螺旋桨优化设计[J]. 船舶力学, 2010, 14(1/2): 20-27.

ZENG Zhibo, DING Enbao, TANG Denghai. Ship propeller design optimization based on BP neural network and genetic algorithm[J]. Journal of Ship Mechanics, 2010, 14(1/2): 20-27.

[3]ZENG Zhibo, KUIPER G. Blade section design of marine propellers with maximum cavitation inception speed[J]. Journal of Hydrodynamics, Series B, 2012, 24(1): 65-75.

[4]王鹏, 黄帅, 朱舟全. 群智能算法在螺旋桨参数优化设计中的应用[J]. 计算机科学, 2013, 40(11A): 73-76. WAND Peng, HUANG Shuai, ZHU Zhouquan. Application of swarm intelligence optimization algorithm in parameter optimization design of propeller[J]. Computer Science, 2013, 40(11A): 73-76.

[5]常欣, 郭春雨, 孟祥印, 等. 基于粒子群算法的水翼剖面优化设计[J]. 船舶工程, 2010, 32(5): 1-3, 26.

CHANG Xin, GUO Chunyu, MENG Xiangyin, et al. Design of hydrofoil section based on particle swarm optimization[J]. Ship Engineering, 2010, 32(5): 1-3, 26.

[6]王超, 熊鹰, 何苗, 等. 粒子群算法在大侧斜螺旋桨侧斜分布优化中的应用[J]. 上海交通大学学报：自然科学版, 2012, 46(3): 398-403.

WANG Chao, XIONG Ying, HE Miao, et al. Application of particle swarm optimization theory in skew distribution of highly skewed propeller[J]. Journal of Shanghai Jiao Tong University： Natural Science Edition, 2012, 46(3): 398-403.

[7]许平, 姜长生. 基于遗传算法及Hicks-Henne型函数的层流翼型优化设计[J]. 空军工程大学学报：自然科学版, 2009, 10(1): 13-16.

XU Ping, JIANG Changsheng. Optimization design of laminar aerofoil based on genetic algorithms and Hicks-Henne shape function[J]Journal of Air force Engineering University： Natural Science Edition, 2009, 10(1): 13-16.

[8]周明, 孙树栋. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 2005: 35-65.

[9]叶金铭, 熊鹰, 高霄鹏, 等. 非空泡螺旋桨低频线谱噪声时域预报方法[J]. 哈尔滨工程大学学报, 2013, 34(1): 1-6.

YE Jinming, XIONG Ying, GAO Xiaopeng, et al. Prediction method of low-order blade frequency noise of non-cavitation propeller in time domain[J] Journal of Harbin Engineering University, 2013, 34(1): 1-6.

[10]覃新川, 黄胜, 常欣. 船舶螺旋桨面元法的改进[J]. 华中科技大学学报：自然科学版, 2007, 35(5): 65-68.

QIN Xinchuan, HUANG Sheng, CHANG Xin. Improvement of the ship panel method[J]. Journal of Huazhong University of Science and Technology： Nature Science Edition, 2007, 35(5): 65-68.

Optimal design of propellers considering beyond-design conditions

CHANG Xin, SUN Shuai, WANG Chao, MO Tao

(College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract：In order to improve propeller performance, an optimal method for the propeller efficiency was studied in beyond-design conditions. An optimal mathematical model was established by taking the open water efficiency corresponding to different speeds around the designed velocity of the parent propeller as the objective function, taking the radial distribution of pitch ratio as an optimization variable, and taking the thrust, torque, and cavitation performance of the propeller as constraints. The multi-objective optimization model was changed into a single-objective optimization model by weighting efficiency of different inlet velocity points and weighted sums. The panel method was used to solve the propeller hydrodynamic performance and cavitation performance was described by the BaiLiEr merchant margin line. Based on the simple genetic algorithm, the optimization model was solved, and then the optimized radial distribution of the pitch ratio was obtained. A comparison was made between the optimized in-water performance and the optimized design results. It shows that propeller optimization that only considers designed conditions often fails to achieve the expected energy-saving because of ship speed changes. The efficiency of multiple operating points around the design speed should be considered.

Keywords：propeller optimization; optimal design; beyond-design conditions; weight; simple genetic algorithm; pitch ratio distribution; open water efficiency

通信作者：孙帅，E-mail:sunshuaidoc@163.com.

作者简介：常欣(1978-), 男, 副教授,博士；

基金项目：国家自然科学基金资助项目 (51379040).

收稿日期：2014-10-27.网络出版日期：2015-11-06.

中图分类号：U661.31

文献标志码：A

文章编号：1006-7043(2015)12-1544-05

doi:10.11990/jheu.201410067