基于超扩展规则的动态在线推理算法

刘磊, 牛当当, 李壮, 吕帅

(吉林大学 计算机科学与技术学院,吉林 长春130012)

基于超扩展规则的动态在线推理算法

刘磊, 牛当当, 李壮, 吕帅

(吉林大学 计算机科学与技术学院,吉林 长春130012)

摘要：为了提高扩展规则的扩展性能，提出了超扩展规则，并证明了其与扩展负超归结之间的关联关系。KCER算法中使用扩展规则扩展子句，利用超扩展规则替换扩展规则能够更清晰地展示扩展过程，因此提出了基于超扩展规则的动态在线推理算法IKCCER。IKCCER采用离线编译和在线推理过程交互执行的方式，在保持推理效率不变的同时，其空间复杂性为KCCER算法空间复杂性的2/(n+1)，其中n为输入子句集的子句数。

关键词：自动推理；知识编译；扩展规则；超扩展规则；动态在线推理

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20151104.1633.004.html

吕帅(1981-)，男，讲师.

许多约束问题仅判定是否可满足是远远不够的，如将概率推理问题[1]、一致性概率规划问题[2]转换为命题公式集后，除了判断可满足性，还需求解#SAT问题，即计算该公式集中的模型数。求解#SAT问题的方法通常可分为离线推理和知识编译后在线推理。

在离线推理的研究中，在扩展规则提出之前，绝大多数#SAT问题的求解算法都是基于#DPLL算法设计的[3]。林海等[4]提出了扩展规则推理方法(extension rule，ER)，被著名人工智能专家Davis称为与归结方法“互补”的方法。扩展规则推理方法通过计算输入子句集所能扩展出的极大项数来判断其可满足性及模型数。殷明浩等[5]基于容斥原理提出了解决ER算法空间复杂性问题的CER算法；赖永等[6]提出了#ER算法，并结合#DPLL算法和#ER算法提出了求解效率较高的#CDE算法。

知识编译是知识表示与推理领域的一个重要论题，它试图将问题转化为多项式时间内能够得到解决的表示形式。Selman[7]设计了将原子句集转化为等价Horn子句集的编译方法，但并非所有子句集都存在与其等价的Horn子句集，因此该方法不完备。Val[8]提出了一种精确的知识编译方法，并通过运行一个完备的求本原蕴含式的算法过程保证编译后子句集上的单元归结完备。Marquis[9]提出了一种基于本原蕴含式的知识编译方法。Schrag[10]提出了一种对偶的基于本原蕴含的方法。Darwiche[11]将子句形式转换为可分解否定范式DNNF，并给出知识编译的发展图谱。在扩展规则的基础上中，Lin等[12]提出了一种基于扩展规则的知识编译方法KCER，可以将子句集编译为EPCCL理论。殷明浩等[5]提出了用于求解模型计数问题的KCCER算法。刘大有等[13]基于扩展规则提出了一种新的知识编译算法C2E，该算法具有较高的编译效率。

传统的扩展规则难以直接利用一个文字集对一个子句进行扩展，因此本文提出超扩展规则(hyper extension rule，HER)，描述了利用超扩展规则的推理过程，并证明了超扩展规则与扩展负超归结的等价性。基于扩展规则能够将一个公式集编译为EPCCL理论，然而现有编译方法由于扩展规则的限制，在编译过程中容易出现内存溢出的现象。本文针对基于扩展规则的知识编译过程，提出了基于超扩展规则的动态在线推理算法IKCCER，解决了采用离线编译和在线推理过程交互执行的方式，在保持推理效率不改变的同时，降低空间复杂性，有效解决内存溢出问题。

1超扩展规则

定义1(扩展规则)[4]给定一个子句C和一个变量集M，D= {C∨a,C∨a}，其中a∈M并且a和a都不在C中出现，将C到D的推导过程称为扩展规则，D中的子句称为C扩展得到的结果，并且C≡D。

扩展规则要求一个子句结合一个变量进行扩展，本文提出超扩展规则，允许一个子句结合另一个子句进行扩展。为了表示方便，定义子句C的(原子)变量集合为V(C)，子句集F的(原子)变量集合为V(F)。

定义2(超扩展规则)给定2个子句C和A，D= {C∨A,C∨A}，其中V(C)∩V(A) = Ø，将C到D的推导过程称为超扩展规则，D中的元素为C应用超扩展规则的结果。

定理1超扩展规则中，子句C及扩展结果D是等价的。

证明：可以通过真值表证明子句C及其扩展结果语义上是等价的。证毕。

与经典扩展规则不同，超扩展规则用子句A对子句C进行扩展，但这种扩展方法产生的C∨A为非子句形式(C∨A为标准子句形式)，因此需要对C∨A以适当形式展开。假设A= {b1,b2，…,bn}，则运用德摩根律，E= {C∨A} = {C∨(b1∨…∨bn)} = {C∨b1,C∨b2…,C∨bn}。上述展开过程是语义等价的，但由于每个bi(i= 1,…,n)两两不同且均不在C中出现，所以E的互补因子较低，难以利用扩展规则的推理特性。为了保证扩展结果子句间的互补性，采用如下方法展开[14]：

(1)

称式(1)的展开过程为互补展开，则E= {C∨A} = {C∨b1,C∨b1∨b2,…,C∨b1∨…∨bn-1∨bn}，进而D= {C∨b1∨…∨bn,C∨b1,C∨b1∨b2,…,C∨b1∨…∨bn-1∨bn}。

定理2依赖式(1)的互补展开保证了超扩展规则的等价性，并且展开结果子句之间存在互补文字对。

证明：假设A= {b1, b2…,bn}，由于C本身对扩展结果性质没有影响，只需要证明：1)A=(b1∨…∨bn)与Z= {{b1},{b1∨b2},…,{b1∨…∨bn-1∨bn}}等价；2){b1,b1∨b2,…,b1∨…∨bn-1∨bn}子句之间存在互补文字对。其中2)显然成立。下面证明1)。

综上，结论1)得证，进而定理2成立。证毕。

超扩展规则能够利用一个子句扩展另一个子句，并且利用互补展开在保证可满足性的前提下保证了扩展之后的子句间存在互补文字对，这使得扩展过程能够高效进行并得到能够发挥扩展规则推理方法特性的理论。超扩展规则同时也是一种等价性规则，可以利用超扩展规则和推导规则作为核心推理规则构建新的推理框架。

2基于超扩展规则的定理证明方法

定义3一个非重言式子句是集合M上的极大项当且仅当包含集合M上的所有原子或其否定。

基于超扩展规则将一个子句集扩展为极大项集的过程为：

首先对子句集中每一个子句做扩展，假设变量集为M，则D= {C∨{M-V(C)},C∨{M-V(C)}}，将新扩展的子句集D与原子句集合并，并去掉重复子句或可被蕴含的子句，如此不断扩展，最终会得到一个极大项集。

定理3利用超扩展规则扩展出的极大项集与原子句集等价。

证明：扩展过程中仅使用超扩展规则和推导规则。根据定理2，超扩展规则保证了扩展结果与原子句集等价，因此，整个扩展过程中是等价变换，利用超扩展规则扩展出的极大项集合与原子句集等价。证毕。

定理4在命题逻辑中，基于超扩展规则的极大项扩展方法是有效完备的。

证明：类似文献[4]中定理3.2的证明过程，上述定理显然成立。证毕。

定理5给定一个子句集F由V(F)上的极大项组成，|V(F)| =m，则F不可满足当且仅当F中包含2m个互不相同的极大项。

定理6[5]给定一个子句集F由V(F)上的极大项组成，|V(F)| =m，则F的模型数为2m-S，当且仅当F中包含S个互不相同的极大项。

定理6给出了模型数与极大项的关系，如果要计算一个子句集的模型数，首先需要将子句集扩展为与其等价的极大项集，再根据定理6计算出原子句集的模型数。

超扩展规则能够将一个子句集扩展为极大项集，然而扩展结果的子句集规模往往较大，最坏情况下的空间复杂性是指数级的。实际上并不需要将所有的极大项都扩展处理，只需要计算它的个数即可。若一个子句集能够扩展出的极大项集中元素个数为S，则子句集包含2m-S个模型。容斥原理可以高效实现模型个数的计算，并在基于扩展规则的模型计数方法中采用，具体细节请参阅文献[5]。

3超扩展规则与扩展负超归结的关联关系

Peter等给出了负超归结的基本定义[15]，该定义可以进一步扩展。

定义4 (扩展负超归结，extension negative hyper resolution)假设存在子句集{Ci∨x1∨…∨xi-1∨xi} (i= 1,2，…,r)和子句C0∨x1∨…∨xr，其中xi是文字，C0和Ci是负文字的析取形式，且有可能为空，则可以直接归结出C0∨C1∨…∨Cr，这种归结方式称为扩展负超归结。

上述归结方式可以通过有序弱化并使用扩展规则予以证明，如图1所示。

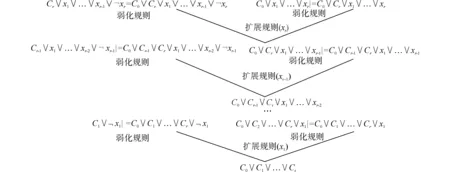
图1　扩展负超归结的归结树Fig.1　The resolution tree of extension negative hyper resolution

扩展负超归结也可以通过弱化规则和超扩展规则直接证明。

假设C=C0∨C1∨…∨Cr，则定义5中所有子句中的Ci(i= 0,1,…,r)，可以通过弱化规则得到子句C，即定义5中所有子句的弱化结果可以表示为{C∨x1∨…∨xr,C∨x1,C∨x1∨x2,…,C∨x1∨…∨xn-1∨xn}，即超扩展规则的扩展结果D的形式。根据定理1可知：该扩展结果D与C等价，即可以通过定义5中的所有子句归结出C0∨C1∨…∨Cr。

推论1若所有Ci(i= 0,1,…,r)均相同，则超扩展规则与扩展负超归结等价。

定义5(混合负超归结，hybrid negative hyper resolution)假设存在子句集{Ck∨xk,Ck+1∨xk∨xk+1,…,Ci∨xk∨…∨xi-1∨xi| 1≤k≤i≤r}和子句C0∨x1∨…∨xr，其中xi是文字，C0和Ci是负文字的析取形式，且有可能为空，则可以直接归结为C0∨C1∨…∨Cr，这种归结方式称为混合负超归结。

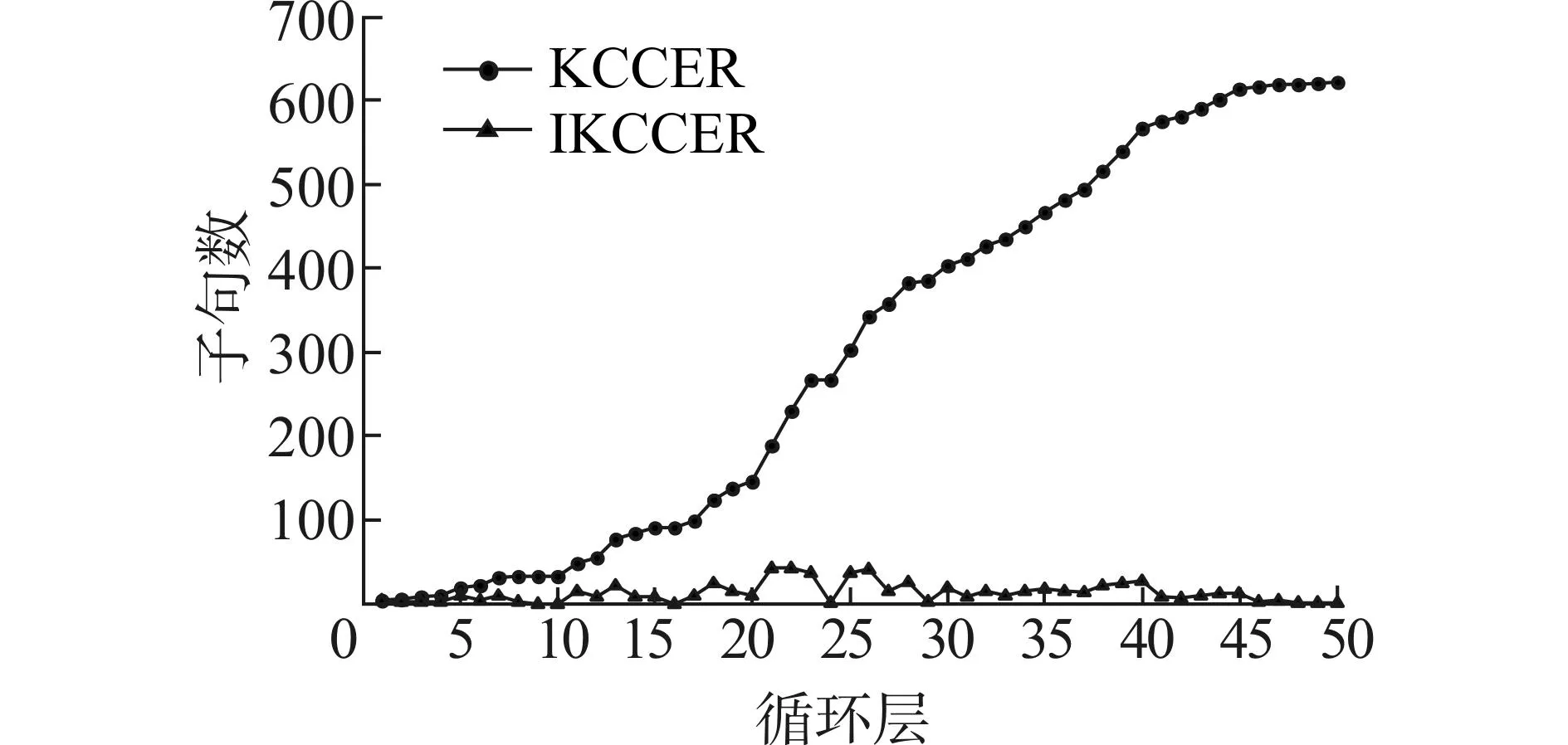
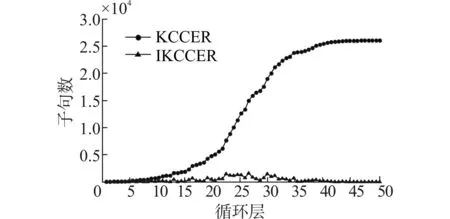
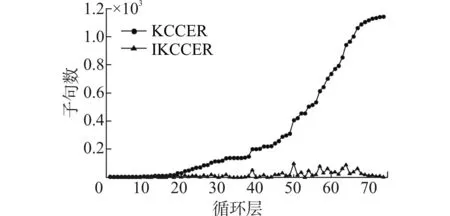
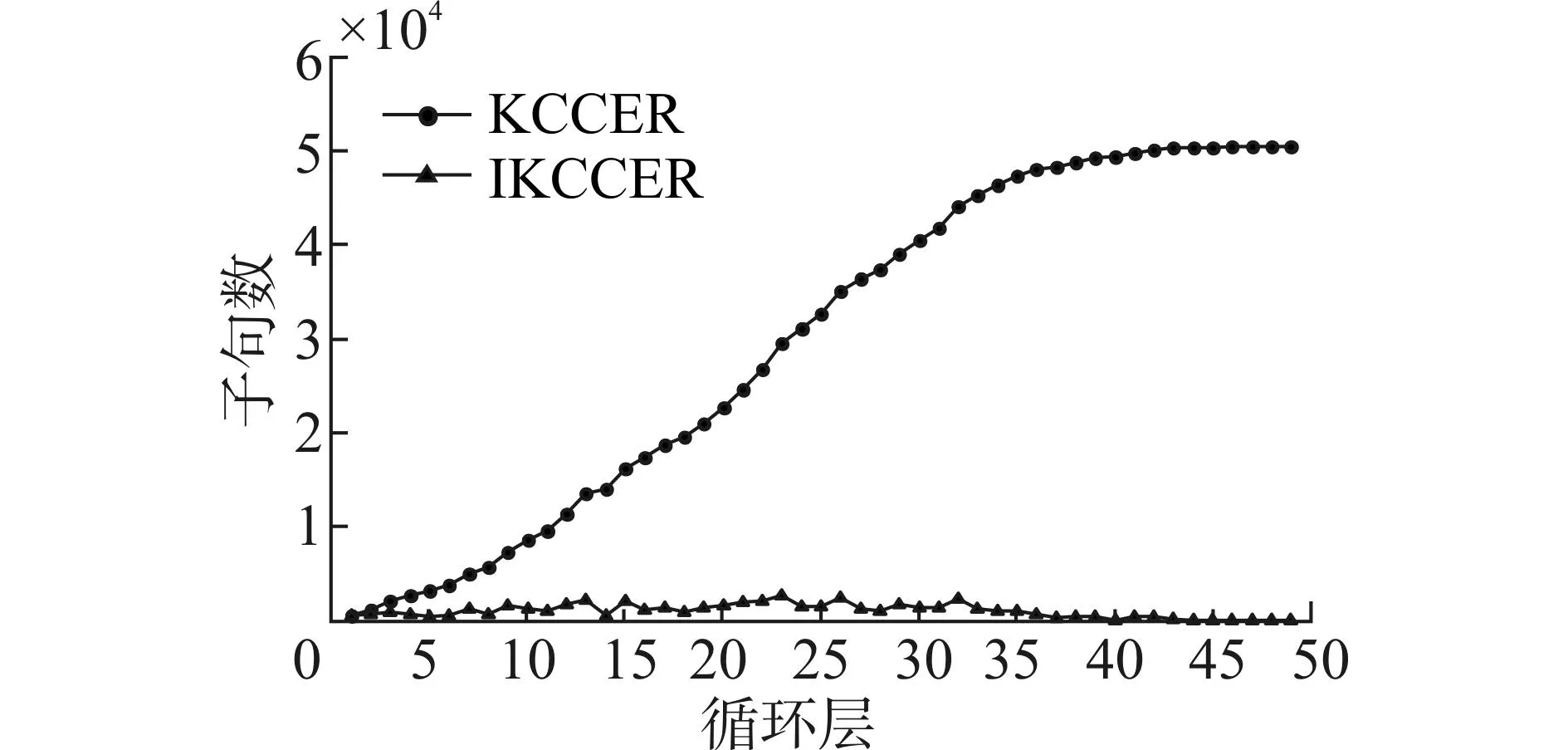
负超归结与扩展负超归结为混合负超归结的特殊形式。当k=i时，混合负超归结等价于负超归结；当k= 1时，混合负超归结等价于扩展负超归结；当任一k满足1

4基于超扩展规则的动态在线推理算法IKCCER

本文在EPCCL理论编译过程中利用超扩展规则替换了扩展规则，设计并实现了动态在线推理算法IKCCER，该算法不需要保存临时变量，从而大幅度降低了知识编译求解#SAT问题的空间复杂性。实验结果表明该算法具有较好的存储开销。

4.1　IKCCER算法

利用扩展规则可以将一个子句集编译成EPCCL理论。在EPCCL理论中，解决推理问题只需要多项式时间，KCER算法为将一个子句集编译成EPCCL理论的最具代表性的高效算法，其具体流程参见文献[12]。

用超扩展规则代替了经典扩展规则，能更清晰地描述整个扩展过程(体现在算法1第10行)。当子句Ci和Cj不存在互补文字对且彼此不蕴含时，只需要求解差集Ci-Cj，就能找到Cj需要扩展的所有文字，然后利用超扩展规则，利用这些文字组成的子句对Cj进行扩展。

殷明浩等基于KCER算法提出了KCCER算法，是一种高效的#SAT问题计算方法，对于互补因子较高的公式集求解，能够取得非常好的求解效率[5]。由于离线编译过程通常可以通过前期的理论分析得以有效预处理，所以人们通常只关注在线推理时间，离线时间通常不作为评价标准予以考虑。KCCER算法首先利用知识编译将子句集离线编译为一个EPCCL理论，之后在该理论上在线推理，计算编译后的#SAT问题只需要多项式时间，高效的在线推理性能使得该算法能够用于#SAT问题的高效求解。

研究过程中发现：如果在知识编译过程中进行动态在线推理，则能够减少大量存储空间使用，同时不影响推理过程的时间复杂性。基于此，本文提出了IKCCER算法。

算法1 IKCCER

1.令子句集Σ1= {C1,…,Cn}, Σ2= Σ3= Ø

2.sum = 0, i = 0, j = 0

3.While Σ1≠Ø

4.从Σ1中选择一个子句C，将其加入到Σ2中

5.While i<Σ1的子句数

6.While j<Σ2的子句数

7.If Ci和Cj含互补文字对 Then skip

8.Else if Ci蕴含CjThen 从Σ2中删除Cj9.Else if Cj蕴含CiThen 从Σ1中删除Ci

10.Else将Cj替换为Cj∨{Ci-Cj}∪Cj∨Ci-Cj//超扩展规则

11.j= j+1

12.i= i+1

13.j= 0

14.While k<Σ2的子句数

15.Num=Num+2m-|V(Ck)|

16.k=k+1

17.Σ2=Ø

18.Return 2m-Num

IKCCER算法对KCCER算法的改进之处在于：在一次循环结束后，直接计算出子句集Σ2所能扩展出的极大项数，并删除Σ2。原因在于：若任何一个子句与其他子句存在互补文字对，则它所扩展的任何极大项都不会被其他子句扩展。因此，该算法的动态在线推理过程是正确的。

4.2　IKCCER算法的时间复杂性分析

IKCCER算法与KCCER算法的时间复杂性相同。

1)在线推理时间：首先将EPCCL理论中所有子句能扩展的极大项数，放在知识编译过程中计算，该过程中并没有增加或减少计算量，因此与KCCER算法的在线推理效率相同。

2)离线知识编译时间：由于IKCCER算法同样需要将一个子句集编译为一个EPCCL理论，不可能提前结束，因此离线编译时间与KCCER算法相同。

因此，IKCCER算法与KCCER算法时间复杂性等价。由于IKCCER算法和KCCER算法所需执行时间相同，因此本文不列出实验结果对比分析。仅通过定理7证明IKCCER算法为何不能提前结束。

定理7假设子句集Σ= {C1,…,Cn}，|V(Σ)| = m，在IKCCER算法的知识编译过程中，若已编译的子句集能够扩展的极大项数为2m，则Σ1必为Ø。

证明：知识编译的一次循环，需要找到一个所有子句间存在互补文字对，且与当前Σ1中所有子句存在互补文字对的子句集。假设Σ1不为Ø，则必然存在一个子句与当前编译得到的子句集中所有子句存在互补文字对，则当前编译得到的子句集能够扩展的极大项不会包含该子句所能扩展的极大项，因此与当前扩展的极大项数为2m条件冲突，结论成立。证毕。

4.3　IKCCER算法的空间复杂性分析

IKCCER算法比KCCER算法的空间复杂性低。由于KCCER算法需要不断保存中间过程，因此始终需要一个数组保存中间结果，增加了存储空间使用量。IKCCER算法采用动态在线推理，不保存中间结果。假设平均每次能够扩展出k个子句，则KCCER算法每次需要增加k个子句的存储空间，在执行过程中累计需要保存k+2k+3k+…+nk= (n2+n)k/2个子句的存储空间，而IKCCER算法只需要nk个子句的存储空间，为KCCER算法的2/(n+1)，这对于大规模子句集来说效果更加明显。

为了说明存储空间的压缩效果，对变量数m为15、20和25，子句数n为50、75和100的随机3-SAT问题予以测试，实验结果分别如图2~4所示。

(a)内存消耗3-SAT(15，50)

(b)内存消耗3-SAT(20，50)

(c)内存消耗3-SAT(25，50)图2　IKCCER和KCCER空间开销对比(n = 50)Fig.2　The comparison of spending space between IKCCER and KCCER (n = 50)

(a)内存消耗3-SAT(15，75)

(b)内存消耗3-SAT(20，75)

(c)内存消耗3-SAT(25，75)图3　IKCCER和KCCER空间开销对比(n = 75)Fig.3　The comparison of spending space between IKCCER and KCCER (n = 75)

(a)内存消耗3-SAT(15，100)

(b)内存消耗3-SAT(20，100)

(c)内存消耗3-SAT(25，100)图4　IKCCER和KCCER空间开销对比(n = 100)Fig.4　The comparison of spending space between IKCCER and KCCER (n = 100)

需要注意的是：由于子句规模变大后，所对比的KCCER算法存储空间需求远远高于本文提出的IKCCER算法，便于对比分析，图2和图3的纵坐标为线性坐标，而图4选用了指数纵坐标。图2~4中的横坐标代表正在进行的循环层，纵坐标代表了需要的额外存储空间，用子句数刻画。

实验结果表明：1)图2和图3的对比结果容易看出：IKCCER算法的存储开销基本上无明显变化，保持较低的存储空间开销，直到算法执行完毕；而KCCER算法的存储空间开销随着循环执行持续增加；2)循环刚开始，IKCCER算法与KCCER算法所需的额外存储空间相近；3)随着循环的逐步执行，IKCCER算法所需存储空间明显少于KCCER算法，甚至相差4~5个数量级；4)图3中IKCCER曲线出现若干孤立点的情况，是由于测试结果为0而无法在指数级坐标很好的表示，并不影响整体结论；5)图4中IKCCER曲线波动较大，但在线性坐标下(类似图2和图3)存储开销基本趋于稳定。

在小规模子句集上的测试结果显示了IKCCER算法的存储开销优势，更大规模的测试样例对于KCCER算法在系统运行空间上是难以承受的，上述测试结果(IKCCER算法存储开销基本上无明显变化)使得有理由相信IKCCER算法将继续保持该优势，而原算法将难以使用。

因此，本文提出的IKCCER算法具有很好的存储空间开销。由于经典扩展规则需要保存中间结果较多，并且在扩展之后子句集规模较大，利用动态在线推理的IKCCER算法能够明显降低空间复杂性，从而解决了KCCER算法容易内存溢出的问题。

5结束语

本文提出了超扩展规则，并证明了超扩展规则和扩展负超归结的关联关系；重写了KCER算法，在KCCER算法的基础上提出了IKCCER算法，解决了KCCER算法应用在大规模子句集中容易产生内存溢出的问题。实验结果表明，采用动态在线推理策略的IKCCER算法，在存储空间利用方面存在着巨大的优势，能够适应于大规模子句集模型计数问题的求解。

该算法可以作为扩展规则方法的典型，在不适合归结方法求解的大规模子句集可满足性问题和模型计数问题等领域发挥子句集互补特性，为高效推理提供了可能。

参考文献：

[1]MAJERCIK S M, LITTMAN M L. Contingent planning under uncertainty via stochastic satisfiability[J]. Artificial Intelligence, 2003, 147(1/2): 119-162.

[2]PALACIOS H, GEFFNER H. Compiling uncertainty away in conformant planning problems with bounded width[J]. Journal of Artificial Intelligence Research, 2009, 35: 623-675.

[3]BIRNBAUM E, LOZINSKII E L. The good old Davis-Putnam procedure helps counting models[J]. Journal of Artificial Intelligence Research, 1999, 10: 457-477.

[4]LIN Hai, SUN Jigui, ZHANG Yimin. Theorem proving based on the extension rule[J]. Journal of Automated Reasoning, 2003, 31(1): 11-21.

[5]殷明浩, 林海, 孙吉贵. 一种基于扩展规则的#SAT求解系统[J]. 软件学报, 2009, 20(7): 1714-1725.YIN Minghao, LIN Hai, SUN Jigui. Solving #SAT using extension rules[J]. Journal of Software, 2009, 20(7): 1714-1725.

[6]赖永, 欧阳丹彤, 蔡敦波, 等. 基于扩展规则的模型计数与智能规划方法[J]. 计算机研究与发展, 2009, 46(3): 459-469.LAI Yong, OUYANG Dantong, CAI Dunbo, et al. Model counting and planning using extension rule[J]. Journal of Computer Research and Development, 2009, 46(3): 459-469.

[7]SELMAN B, KAUTZ H. Knowledge compilation using horn approximations[C]//Proceedings of the 9th National Conference on Artificial Intelligence. Anaheim, USA, 1991: 904-909.

[8]DEL VAL A. Tractable databases: How to make propositional unit resolution complete through compilation[C]//Proceedings of the 4th International Conference on Principles of Knowledge Representation and Reasoning (KR’94). Bonn, Germany, 1994: 551-561.

[9]MARQUIS P. Knowledge compilation using theory prime implicates[C]//Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI’95). Montréal, Québec, Canada, 1995: 837-843.

[10]SCHRAG R, MIRANKER D P. Compilation for critically constrained knowledge bases[C]//Proceedings of the 13th National Conference on Artificial Intelligence (AAAI’96). Portland, USA, 1996: 510-515.

[11]DARWICHE A, MARQUIS P. A knowledge compilation map[J]. Journal of Artificial Intelligence Research, 2002, 17(1): 229-264.

[12]LIN Hai, SUN Jigui. Knowledge compilation using the extension rule[J]. Journal of Automated Reasoning, 2004, 32(2): 93-102.

[13]刘大有, 赖永, 林海. C2E: 一个高性能的EPCCL编译器[J]. 计算机学报, 2013, 36(6): 1254-1260.LIU Dayou, LAI Yong, LIN Hai. C2E: An EPCCL compiler with good performance[J]. Chinese Journal of Computer, 2013, 36(6): 1254-1260.

[14]LARROSA J, HERAS F, DE GIVRY S. A logical approach to efficient Max-SAT solving[J]. Artificial Intelligence, 2008, 172(2/3): 204-233.

[15]PETER J, JUSTYNA P. Local consistency and SAT-solvers[J]. Journal of Artificial Intelligence Research, 2012, 43: 329-351.

Dynamic online reasoning algorithm based on the hyper extension rule

LIU Lei, NIU Dangdang, LI Zhuang, LYU Shuai

(College of Computer Science and Technology, Jilin University, Changchun 130012, China)

Abstract：In order to improve the extension ability of extension rules, hyper extension rule(HER) is proposed in this paper, and the relevant relationship between the hyper extension rule and extension negative hyper resolution is proven. HER replaces extension rule(ER) in knowledge compilation using extension rule(KCER), so the extension process can be shown more clearly. Then the dynamic online reasoning algorithm interactive knowledge compilation for counting models using extension rule(IKCCER) is proposed based on HER. It adopts an interactive execution mode between offline compilation and online reasoning process. IKCCER does not change the efficiency of knowledge compilation for counting models using extension rule(KCCER), and its space complexity is 2/(n+1) of KCCER's space complexity (n is the number of clauses of the input CNF formula).

Keywords：automated reasoning; knowledge compilation; extension rule; hyper extension rule; dynamic online reasoning

通信作者：吕帅，E-mail：lus@jlu.edu.cn.

作者简介：刘磊(1960-)，男，教授，博士生导师;

基金项目：国家自然科学基金资助项目(61300049，61402195)；教育部高等学校博士学科点专项科研基金资助项目(20120061120059);吉林省科技发展计划资助项目(20130206052GX，20140520069JH).

收稿日期：2014-04-16.网络出版日期：2015-11-04.

中图分类号：TP301，TP181

文献标志码：A

文章编号：1006-7043(2015)12-1614-06

doi:10.11990/jheu.201404055