载波频偏对OFDM AF中继系统性能的影响*

李巨虎　聂娟

(1.北京林业大学 信息学院, 北京 100083; 2.北京农学院 计算机与信息工程学院, 北京 102206)

载波频偏对OFDM AF中继系统性能的影响*

李巨虎1聂娟2

(1.北京林业大学 信息学院, 北京 100083; 2.北京农学院 计算机与信息工程学院, 北京 102206)

摘要：研究了存在载波频偏的正交频分复用(OFDM)放大转发(AF)中继系统的中断概率和误码率.首先给出了存在载波频偏时系统信噪比及其概率分布,然后推导出瑞利信道中存在载波频偏时系统中断概率和误码率的闭合表达式.为了更加直观,文中还给出了大信噪比时系统中断概率和误码率的错误下界,并通过数值仿真来验证理论分析的正确性.理论分析和仿真结果表明:存在载波频偏时,即使在大信噪比情形下系统的中断概率和误码率并不趋于0,而是趋于错误下界;OFDM AF系统对载波频偏很敏感,随着信噪比的增大,系统性能随着载波频偏的增大迅速变差.

关键词：放大转发;正交频分复用;载波频偏;中断概率;误码率

中继系统能够扩展传输距离及对抗信道衰落,成为无线通信的研究热点,在近几年得到了飞快发展.中继系统的传输机制主要包括放大转发(AF)模式和译码转发(DF)模式.采用AF模式时中继节点不需要对接收数据进行检测和译码,而是简单的放大转发,这样能够减小数据的传输时延而且实现方式简单,因而得到了广泛的应用.正交频分复用(OFDM)因能够对抗信道的频率选择性衰落并消除符号间的干扰而得到了广泛的应用.OFDM AF中继系统综合了AF和OFDM两种技术的优点,成为新一代无线通信的标准.很多文献对OFDM AF中继系统进行了研究.文献[1]研究了瑞利信道中OFDM AF中继系统的性能,给出了中继节点采用固定放大增益时系统的误码率.文献[2- 4]对基于子载波配对的OFDM AF中继系统做了深入研究,首先研究了瑞利信道中基于子载波配对的OFDM AF中继系统的中断概率、中断容量和系统误码率,然后研究了Nakagami-m信道中基于子载波配对的OFDM AF系统的误码率和信道容量.

与OFDM相同,OFDM AF中继系统对载波频率偏移(CFO)非常敏感,载波频率偏移会造成子载波间干扰(ICI),导致系统性能下降.文献[5- 6]针对载波频偏对OFDM系统性能的影响进行了研究,但载波频偏对OFDM AF中继系统性能影响的相关研究不多.文献[7]研究了载波频偏对OFDM AF中继系统信噪比的影响,给出了存在载波频偏时系统信噪比的表达式及系统误码率的仿真结果,但对系统误码率没有做理论分析.文献[8]研究了存在共信道干扰(CCI)和信道估计误差时AF中继系统的中断概率和误码率,给出了其闭合表达式,但共信道干扰和载波频偏引起的干扰有很大的区别.文献[9]研究了由载波频偏引起的子载波干扰,给出了消除子载波干扰和符号间干扰的方法.文献[10]首先利用前导码估计OFDM AF系统的载波频偏,然后根据估计值消除载波频偏.文献[11]通过差分调制(DM)方法来消除载波频偏和信道估计误差对系统性能的影响.

OFDM AF系统存在源节点和中继节点间、中继节点和目的节点间的载波频偏,其对OFDM AF系统性能的影响比OFDM系统复杂得多,不可能借用OFDM系统的结论.另外,现有研究主要集中在消除载波频偏,没有定量分析载波频偏对系统误码率和中断概率的影响.为此,文中研究了瑞利信道中载波频偏对OFDM AF中继系统性能的影响.首先给出了存在载波频偏时的系统模型,然后证明载波频偏引起的子载波干扰的高斯性,推导出系统信噪比表达式及其概率分布,进而根据信噪比的概率分布推导出OFDM AF中继系统存在载波频偏时的中断概率表达式及其下界,并推导了M元正交幅度调制(MQAM)时的系统误码率及其下界,最后对理论分析值和仿真结果进行了比较.

1存在载波频偏时的系统模型

OFDM AF系统采用时分双工模式,其传输模型如图1所示.源节点将数据调制成OFDM信号发送到中继节点,中继节点放大并转发信号,目的节点接收中继节点的信号并解调恢复数据.两跳传输发生在不同时刻、不同节点之间,并假定每跳信号都经历瑞利衰落和加性高斯白噪声(AWGN),这样源节点-中继节点(S-R)信道和中继节点-目的节点(R- D)信道是相互独立的,互不相干的.

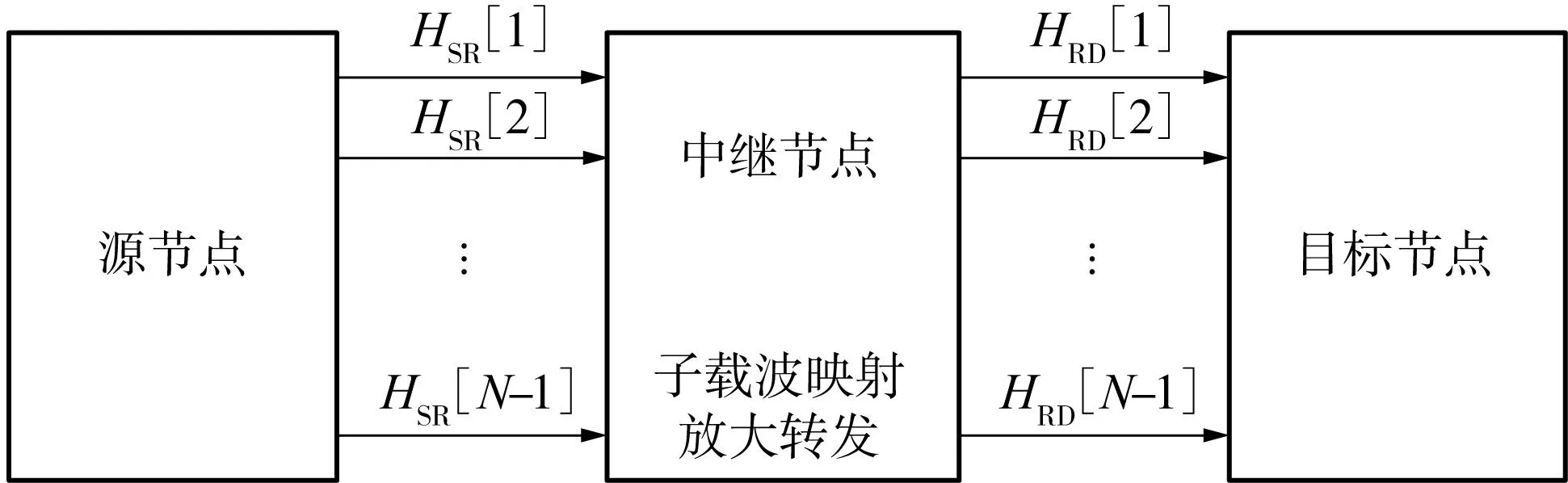
图1　OFDM AF中继系统结构图Fig.1　Structure diagram of OFDM AF relay system

在时间域,存在载波频率偏移时第1跳的基带信号可以表示为[12]

yR[n]=cSR[n](hSR[n]⊗x[n])+wR[n]

(1)

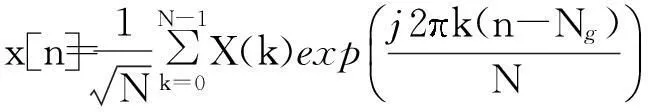
YR[i]=CSR[i]⊗(HSR[i]X[i])+WR[i]=

CSR[0]HSR[i]X[i]+IR[i]+WR[i]

(2)

式中:CSR[i]为cSR[n]的DFT变换,其表达式见式(7);HSR[i]为信道系数hSR[n]的DFT变换;WR[i]为wR[n]的DFT变换;IR[i]为由载波频偏引起的子载波间干扰(ICI),可表示为

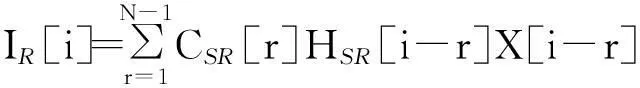
(3)

在时间域,存在载波频率偏移时第2跳的基带信号可以表示为

yD[n]=GcRD[n](hRD[n]⊗yR[n])+wD[n]

(4)

(5)

式中,ES为源节点发送功率,ER为中继节点发送功率.中继节点接收到数据时,把载波数据下变频到基带进行子载波映射.常见的子载波映射有动态子载波映射和随机子载波映射,都是将第1跳的某子载波映射到第2跳的另一子载波.假定将第1跳的第i个子载波映射到第2跳的第k个子载波.在式(4)中,对第k个子载波做DFT,可得到第2跳的频谱表达式,然后把式(2)代入第2跳的频谱表达式,可得

YD[k]=GCRD[k]⊗(HRD[k]YR[i])+WD[k]=

GCSR[0]CRD[0]HRD[k]HSR[i]X[i]+

GCRD[0]HRD[k]WR[i]+GCSR[0]·

GCSR[0]CRD[0]HRD[k]HSR[i]X[i]+

GCRD[0]HRD[k]WR[k]+I1[k]+I2[k]+

I3[k]+WD[k]

(6)

式中:Hij[k]、Wi[k]分别是hi,j[n]和wi[n]的DFT变换;i,j∈{S,R,D};Cij[k]是cij[n]的DFT变换,可表示为

(7)

从式(6)的最后一个等式可知,其第1项为目标信号,但增加了乘性干扰GCSR[0]CRD[0]HRD[k]·HSR[i],最后3项I1[k]、I2[k]和I3[k]是由载波频偏引起的子载波间干扰,可表示为

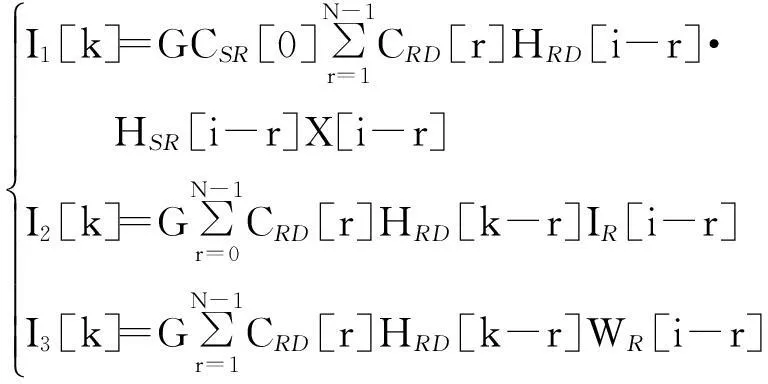
(8)

2子载波干扰的高斯性

在OFDMAF系统中,通常采用M-QAM调制,因此X[i]是零均值的.因为HSR[i]和X[i]是相互独立的,故式(3)中IR[i]的均值为0,方差计算式为

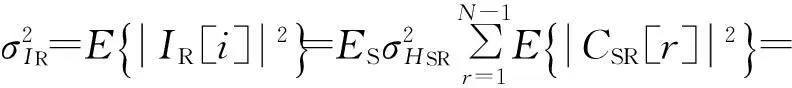
(9)

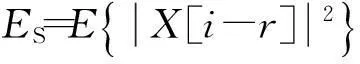
(10)

很多文献把子载波干扰看作高斯噪声处理,但从未证明.文中根据Lyapunov’s中心极限定理[15]证明子载波干扰的高斯性.从式(8)可知,I3[k]是高斯白噪声的加权和,因此I3[k]是高斯噪声,只需证明I1[k]和I2[k]的高斯性即可.要证明I2[k]的高斯性,只需证明IR[i]是高斯噪声即可.为了证明IR[i]的高斯性,首先写出Lyapunov’s中心极限定理.

(11)

以下根据引理1来证明IR[i]的高斯性.

证明根据式(3),IR[i]可重新写为

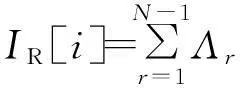
(12)

(13)

根据式(11)和(13),可得

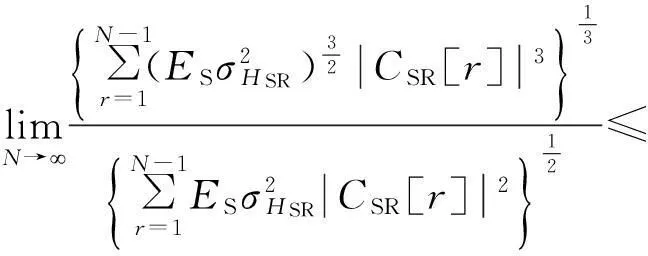
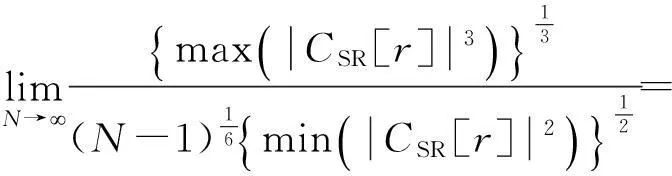
(14)

证毕.

根据以上证明,可以得到IR[i]是高斯随机变量,从而得到I2[k]为高斯随机变量.与证明IR[i]类似,也可以证明I1[k]为高斯随机变量.

3端到端信噪比的概率分布

(15)

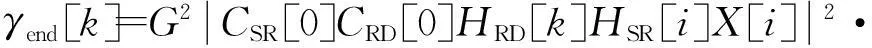
(16)

当系统采用瞬时功率缩放时,根据式(10)和式(5),式(16)可化简为

(17)

引理2[17]X1和X2是相互独立的随机变量,分别服从参数为β1和β2的指数分布,则随机变量X=X1X2/(X1+X2+b)的概率分布函数为

FX(x)=1-2exp(-(β1+β2)x)·

(18)

式中,b为常数,K1(·)为一阶修正的贝塞尔函数,其定义见文献[18]中式(9.6.22).根据引理2,则信噪比γend[k]的概率分布函数可表示为

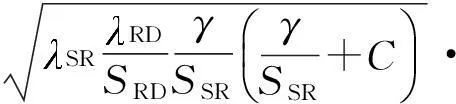
(19)

式(19)对γ求导,利用贝塞尔函数求导等式[19],则信噪比γend[k]的概率密度函数可表示为

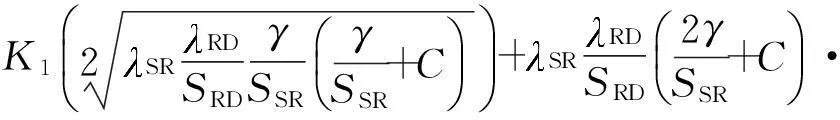
(20)

4性能分析

4.1　中断概率

当系统链路容量不能满足所要求的用户速率时,就会产生中断.对于信噪比来说,当信噪比低于门限值γth后就会发生中断.根据式(19)中信噪比的概率分布和中断概率定义,系统的中断概率表示为

Pout=P[R≤Rth]=P[γend[k]≤γth]=

(21)

(22)

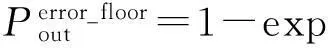
(23)

从式(23)可以看出,系统存在载波频偏且大信噪比时,系统的中断概率并不趋于0,而是趋于错误下界.另外可以看出,源节点和中继节点之间的载波频偏、中继节点与目的节点之间的载波频偏对中断概率错误下界的贡献是不等同的.

4.2　平均差错率

(24)

常规的方法是根据γend[k]的概率分布求得系统误码率.这种方法物理概念清楚,计算复杂.另一种方法是计算信噪比γend[k]的矩生成函数(MGF)Mγend[k](s)=E{exp(-sγend[k])},根据误码率和矩生成函数的关系来计算系统差错率.文中采用矩生成函数方法.利用式(24),则系统的矩生成函数可以表示为

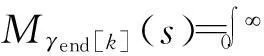
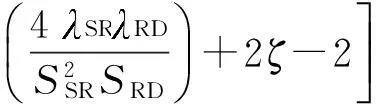
(25)

式中,ζ是欧拉常数.当系统采用M-QAM调制时,根据差错率与矩生成函数的关系[20]:

(26)

(27)

式(27)对γ求导,可以得到系统信噪比的概率密度函数

(28)

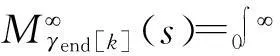
(29)

把式(29)代入式(26)可以得到大信噪比时系统差错率的下界表达式:

(30)

5仿真及结果分析

图2　不同载波频偏时OFDM AF中继系统的中断概率随信噪比的变化Fig.2　Changes of outage probability of OFDM AF relay system with different CFOs

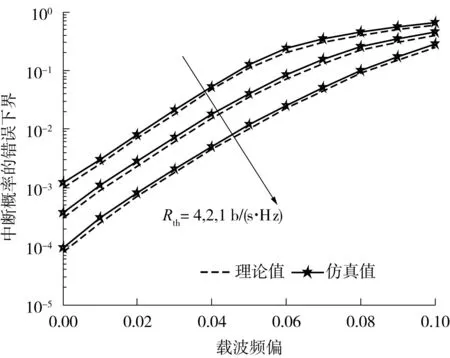
图3　不同链路速率时中断概率的错误下界Fig.3　Error floor of outage probability with different link rates

载波频率偏移不同时OFDMAF系统的中断概率随信噪比的变化如图2所示,图中分别给出了理论分析、数值仿真和中断概率的错误下界.当OFDMAF中继系统的链路速率不同时,中断概率的错误下界随载波频率偏移的变化如图3所示.

OFDMAF系统采用4QAM、16QAM调制且不同的载波频偏时,系统误码率随信噪比的变化如图4所示.OFDMAF中继系统调制方式不同时系统误码率的错误下界随载波频率偏移的变化如图5所示.

图4　不同载波频偏和调制时OFDM AF中继系统的误码率随信噪比的变化Fig.4　Changes of BER of OFDM AF system with different CFOs and different modulations

图5　不同载波频偏时系统误码率的错误下界Fig.5　Error floor of system BER with different CFOs

6结论

文中研究了载波频偏对OFDMAF中继系统性能的影响.根据存在载波频偏时的系统模型,推导出系统端到端信噪比的表达式及其概率分布,又推导出系统的中断概率和误码率的表达式,并进行了数值仿真.文中还对存在载波频偏时系统中断概率及其错误下界、误码率及其错误下界做了深入的研究.结果表明:在大信噪比时,中断概率和误码率不趋于0,而是趋于其错误下界;OFDMAF中继系统对载波频偏很敏感,随着信噪比的增大,系统性能随着载波频偏的增大而迅速变差.

参考文献:

[1]KocanE,Pejanovic-DjurisicM,JavornikT.BERperfor-manceenhancementinOFDMAFfixedgainrelaysystems[C]∥ProceedingsofIEEEEUROCON.Zagreb:IEEE,2013:502-507.

[2]ShahRA,RajathevaN,JiYusheng.OutageprobabilityandoutagecapacityanalysisofcooperativeOFDMsystemwithsubcarriermapping[C]∥Proceedingsof2014IEEEInternationalConferenceonCommunicationsWorkshops.Sydney:IEEE,2014:314-319.

[3]ShahRA,RajathevaN,JiYusheng.Outageanalysesofadual-hopOFDMamplify-and-forwardrelaysystemwithsubcarriermappinginRayleighfading[J].EURASIPJournalonWirelessCommunicationsandNetworking, 2014,2014:209/1-10.

[4]ShahRA,RajathevaN,JiYusheng.AnalysisofBERandcapacityfordual-hopOFDMrelaysystemwithsubcarriermappinginNakagami-mfading[C]∥Proceedingsof2014IEEEInternationalConferenceonCommunicationsWorkshops.Sydney:IEEE,2014:5089-5094.

[5]MaheshRUma,ChaturvediAK.ClosedformBERexpre-ssionsforBPSKOFDMsystemswithfrequencyoffset[J].IEEECommunicationsLetters,2010,14(8):731-733.

[6]DharmawansaP,RajathevaN,MinnH.AnexacterrorprobabilityanalysisofOFDMsystemswithfrequencyoffset[J].IEEETransactionsonCommunications,2009,57(1):26-31．

[7]HuYanxing,JiangYanxiang,YouXiahu.SNRdegradationduetocarrierfrequencyoffsetinamplify-and-forwardrelaysystemforfadingchannels[C]∥ProceedingsofIEEEthe70thVehicularTechnologyConferenceFall.Anchorage:IEEE,2009:1- 4.

[8]YangLiang,QaraqeKhalid,SerpedinErchin,etal.Performanceanalysisofamplify-and-forwardtwo-wayrelayingwithco-channelinterferenceandchannelestimationerror[J].IEEETransactionsonCommunications,2013,61(6):2221-2231.

[9]YaoY,DongX.MultipleCFOmitigationinamplify-and-forwardcooperativeOFDMtransmission[J].IEEETransactiononCommunications,2012,60(12):3844-3854.

[10]HoChinKeong,FungPatrickHoWang,SunSumei.Carrierfrequencyoffsetestimationfortwo-wayrelaying:optimalpreambleandestimatordesign[J].IEEETransactionsonWirelessCommunications,2013,12(4):1898-1909.

[11]WuZhuo,LiGuangxiang,WangTao.Two-wayamplify-and-forwardrelayingwithcarrieroffsetsintheabsenceofCSI:differentialmodulation-basedschemes[J].EURASIPJournalonWirelessCommunicationsandNetworking,2014,2014:111/1-11.

[12]ZhangZhongshan,ZhangWei,TelammbrChintha.Coope-rativeOFDMchannelestimationinthepresenceoffrequencyoffset[J].IEEETransactionsonVehicularTe-chnology,2009,58(7):3447-3459.

[13]SuraweeraHimalA,ArmstrongJean.PerformanceofOFDM-baseddual-hopamplify-and-forwardrelaying[J].IEEECommunicationsLetters,2007,11(9):726-728.

[14]DaoDN,TellamburaC.Intercarrierinterferenceself-cancellationspace-frequencycodesforMIMO-FDM[J].IEEETransactionsonVehicularTechnology,2005,54(5):1729-1738.

[15]FraserDAS.Nonparametricmethodsinstatistics[M].NewYork:Wiley,1981.

[16]SimonMK,AlouiniMS.Digitalcommunicationoverfa-dingchannels[M].2nded.Hoboken:JohnWiley&SonsInc,2005.

[17]ZhangCS,GeJH,LiJ,etal.Performanceanalysisandpowerallocationforatwo-wayamplify-and-forwardrelaywithchannelestimationerrors[J].IETCommunications,2012,6(12):1846-1855.

[18]AbramowitzM,StegunIA.Handbookofmathematicalfunctionswithfigures,graphs,andmathematicaltables[M].9thed.WashingtonDC:USGovernmentPrintingOffice,1970.

[19]GradshteynIS,RyzhikIM.Tableofintegrals,series,andproducts[M].6thed.NewYork:Academic,2000.

[20]SuW,SadekAK,LiuR.Cooperativecommunicationprotocolsinwirelessnetworks:performanceanalysisandoptimumpowerallocation[J].WirelessPersonalCommunications,2008,44(2):181-217.

Effect of Carrier Frequency Offsets on Performance of OFDM AF Relay System

LiJu-hu1NieJuan2

(1. School of Information, Beijing Forestry University, Beijing 100083, China; 2. College of Computer and Information

Engineering, Beijing University of Agriculture, Beijing 102206, China)

Abstract:This paper deals with the bit error rate (BER) and outage probability of a dual hop OFDM AF relay system in the presence of carrier frequency offsets (CFO). First, the signal-to-noise ratio (SNR) of the system and its probability distribution are put forward in the presence of CFO, and then the close-form expressions of the BER and outage probability of the system are derived with CFO in Rayleigh fading channels. In order to provide more insights, the error floors of the BER and outage probability of the system are also obtained. Moreover, a theoretical analysis is proved to be correct by simulation. The theoretical analysis and simulation results indicate that, in the presence of CFO, the BER and outage probability of the system tend to be the error floor but not zero even at a high SNR, and that the performance of OFDM AF relay system is very sensitive to the CFO, and the system performance gets worse rapidly with the increases of the CFO and the SNR.

Key words:amplify-and-forward; orthogonal frequency division multiplexing; carrier frequency offsets; outage probability; bit error rate

中图分类号：TP79

doi：10.3969/j.issn.1000-565X.2015.09.007

作者简介：李巨虎(1978-),男,博士,讲师,主要从事物联网、无线通信等研究.E-mail: lijuhu@bjfu.edu.cn

*基金项目：北京林业大学中央高校基本科研业务费专项资金资助项目(TD2014- 01);北京市教委科技面上资助项目(KM20151002)

收稿日期：2015-03-16

文章编号：1000-565X(2015)09-0039-08

Foundation item： Supported by the General Program of Beijing Committee of Education Science and Technology(KM20151002)