基于联盟形成博弈论的异构无线传输速率分配*
2015-02-18刘娇蛟马碧云
刘娇蛟 马碧云
(华南理工大学 电子与信息学院, 广东 广州 510640)
基于联盟形成博弈论的异构无线传输速率分配*
刘娇蛟马碧云
(华南理工大学 电子与信息学院, 广东 广州 510640)
摘要:针对异构无线网络合作传输的速率分配问题,在联盟效用函数中引入传输功耗,根据融合-分裂原则建立稳定的合作联盟,再用联盟形成博弈论对动态速率分配进行建模,进而提出了一种动态的速率分配算法.为了最大化联盟收益,文中通过求导计算不同网络的传输速率.这个基于融合-分裂的联盟形成和联盟内速率分配过程不断进行,直至业务流传输结束.仿真实验表明,该算法可根据终端位置动态调整参数与传输的网络联盟结构,以低功耗获取高联盟收益.
关键词:合作传输;速率分配;博弈论;Sharpley值
随着通信技术的快速发展,各种无线网络大量共存,在多网重叠覆盖区域通过异构网络实现合作传输是解决高速无线通信的有效方法.同时,越来越多的移动终端(MT)具有多网接入能力,即多模终端,用户希望利用无线接入完成多任务的需求越来越多,如无线家庭、无线办公室、无线会议室等.然而,现有终端大多只能选择接入某个网络,并且这个选择依赖于用户的经验和使用习惯,需要用户了解不同网络的状态和不同业务的需求,盲目接入常导致接入困难、服务质量不高和网络拥塞频繁.为了解决这些问题,国内外学者在网络接入控制、网络选择和资源分配等方面不断展开研究[1-3].其中,如何把数据流分配到负载不同的网络成为资源分配的难点.
因工作频段不同,故不少异构网络可共存,或者通过跳频技术进行避让.如果能根据业务需求和网络负荷控制多业务在多网络的接入与资源调度,即可通过网络协作提高传输能力.其中,速率分配就是研究如何把数据流拆分到多个网络进行合作传输,相关研究逐渐引起不少学者的关注[4-8].针对异构蜂窝网的速率分配问题,文献[4]根据所有用户的感知视频质量进行建模并采用原始对偶近似法解决这个NP难题.文献[5]在特定时延条件下应用比例公平性对室内异构网络环境中的资源分配进行建模,并应用分布式算法解决此优化问题.可见,不同场景的异构网络资源分配可以根据不同评价指标进行建模,对应的优化问题常常是个NP难题,如何解决该难题是资源分配的研究重点.然而,博弈论旨在研究稀缺资源的分配,其研究方法和数学模型逐渐成熟,研究结果可直接用于解决异构网络的速率分配问题.文献[6]应用协商对策论研究宽带网络通过固定链路传输弹性业务的速率控制问题.第四代移动通信中异构网络接入的带宽分配可以采用非合作博弈论建模[7].针对网络的异构性,文献[8]使用拍卖博弈论对频谱租借进行建模,实现了非对称合作传输.文献[9-10]采用加权协商对策论对异构网络的速率分配问题进行了研究.文献[11]使用演化博弈论来解决宏蜂窝网络中自组织小蜂窝的资源调度问题.然而,上述研究以全联盟最优为前提,认为所有网络都参与传输可提高整体收益,没有充分考虑数据传输功耗.事实上,不同网络的数据传输功耗具有异构性,全联盟并不总是有利于提高联盟收益,而且不同网络的传输能力会随着信道质量、传输距离等的变化而变化.如图1所示,假定某个MT在3个网络的覆盖范围内,且离第1个接入点(AP1)最近.随着MT按图示方向移动,它在网络1中的信道衰减会增大,传输功耗也相应增大.因此,网络1中数据传输的获益可能被功耗完全抵消,在联盟中保留网络1不利于获取更多的联盟收益.因此,合作传输的联盟结构应该随时而变,以更好地适应终端位置、网络负荷的变化,兼顾传输功耗和网络性能.
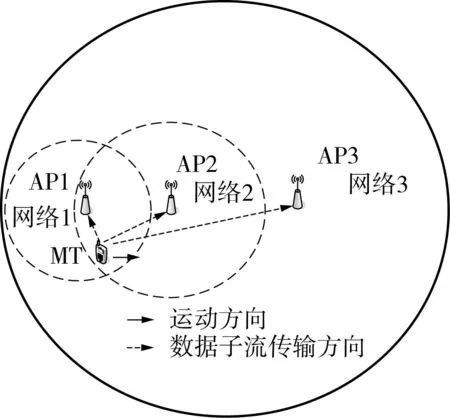
图1 速率分配示意图Fig.1 Schematic diagram of rate allocation
文中引入传输功耗构造联盟效用函数,用联盟形成博弈论对动态速率分配进行建模,利用融合-分裂原则实现了动态联盟形成算法,并对速率分配进行了仿真实验.
1速率分配的数学模型
在合作传输中,业务流可以分发到不同网络进行传输.如图1所示,随着MT的移动,它到AP2的距离减小,信道衰减和传输功耗会随之减小.可见,数据传输功耗会随着终端移动而变化,合作传输的网络联盟也应该随之调整.
1.1 传输模型
假设MT在网络i的传输速率为ri,则网络收益Ui可用网络吞吐量描述[12],即
Ui=wilog2(1+ri)
(1)
式中,wi是单位吞吐量的收益,可理解为网络i向服务接受者收取的服务单价.
如果不考虑多径效应和阴影效应等因素,网络i无线信道传输模型的路径损耗为
Li=Lfsi=32.44+20lgdi+20lgfi
(2)
式中:Lfsi为自由空间的电波传输损耗;di为电波的传播距离,即终端到网络i无线接入点APi的距离;fi为无线信道的工作频率.
此外,网络i的路径损耗也可以用发射功率Ps,i和接收功率Pr,i表示,即
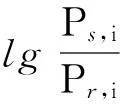
(3)
联合式(2)、(3)可知
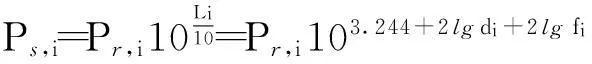
(4)
根据香农定理,高斯白噪声信道可达的最大传输速率C=Blog2(1+S/N),其中C为信道的极限传输速率,B为信道带宽,S为信道的平均接收功率,N为信道的平均噪声/干扰功率.在有噪声/干扰的情况下,为了获得最大传输速率ri所需的最低接收功率为
Pr,i=Ni(2ri/Bi-1)
(5)
因此,发射功率可以表示为
Ps,i=Ni(2ri/Bi-1)103.244+2lgdi+2lgfi
(6)
为了和收益函数在计算单位上统一,定义数据传输的代价函数如下:
Ei=βiPs,i
(7)
其中,βi可理解为传输中消耗单位终端功耗所支付的代价,或者合作时消耗单位终端功耗的不满意度,其取值可以根据网络状态进行设定,网络负荷重时βi较大,反之βi较小.结合网络收益和传输功耗,通过网络i传输业务流的效用函数可表示为

(8)
1.2 效用函数
假定网络和MT是合作传输的理性参与者,它们组成合作联盟G,该联盟的效用函数如下:
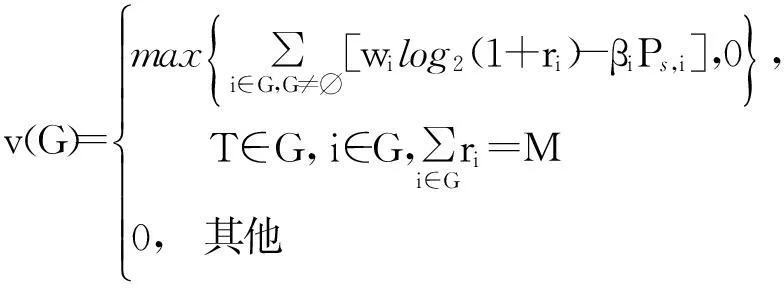
(9)
式中,M为待传输业务流速率,T为移动终端,i为参与联盟的网络.文中研究各网络提供的总带宽大于用户带宽需求时的速率分配方法,以使用户和网络组成的联盟效益最优.当联盟中各网络提供的带宽总和小于用户带宽需求时,每个网络只能以自己所能提供的最大带宽为终端提供服务,文中暂不探讨.从式(9)可知,只有当联盟同时包含网络和MT,并且联盟内网络的可用带宽之和大于用户带宽需求时,合作才有效,才能产生效益.此外,当总的数据传输功耗大于网络吞吐量总收益时,理性参与者趋于离开该联盟,联盟无法形成,效用值为0.
如果传输距离di、信道工作频率fi和信道噪声功率Ni的取值已确定,则可证明

(10)
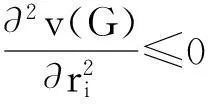
如果只考虑网络的吞吐量收益,不考虑传输功耗,令βi=0,则式(9)变成

(11)
式(11)等同于采用Nash协商对策论对速率分配进行建模[10,13],故基于Nash协商算法的速率分配可视为本文建模的特例.
2联盟形成博弈论
在合作传输中,异构网络和MT被视为理性参与者,它们根据自己的收益决定是否参与联盟,此过程可用联盟形成博弈论进行建模.如果考虑联盟形成代价,不具备超可加性,理性参与者出于自身利益的考虑会退出联盟或者重构联盟,故联盟结构需要进行动态调整.所谓的联盟结构是所有参与者集合的一个划分,对于可转移效用的博弈,最优的联盟结构意味着该结构可使参与者的效益达到帕累托最优.文中采用融合-分裂原则找到最优联盟结构,详细可参见参考文献[14-16].
根据联盟形成博弈论,假设合作参与者集合K′={1,2,…,K},可转移效用函数的特征值定义为v:2K′→R.那么,每个联盟G⊆K′对应的收益可以按照特定公平性原则分配给参与者.假设参与者i(i∈G)从联盟中获得的回报为xi,对于静态的联盟结构G′={G1,G2,…,Gm},联盟博弈可定义为三元组(K′,v,G′).
对于两个不相交的联盟Gi,Gj⊂K′,效用可转移博弈的超可加性是
v(Gi∪Gj)≥v(Gi)+v(Gj)
(12)
s.t. Gi∩Gj=∅.
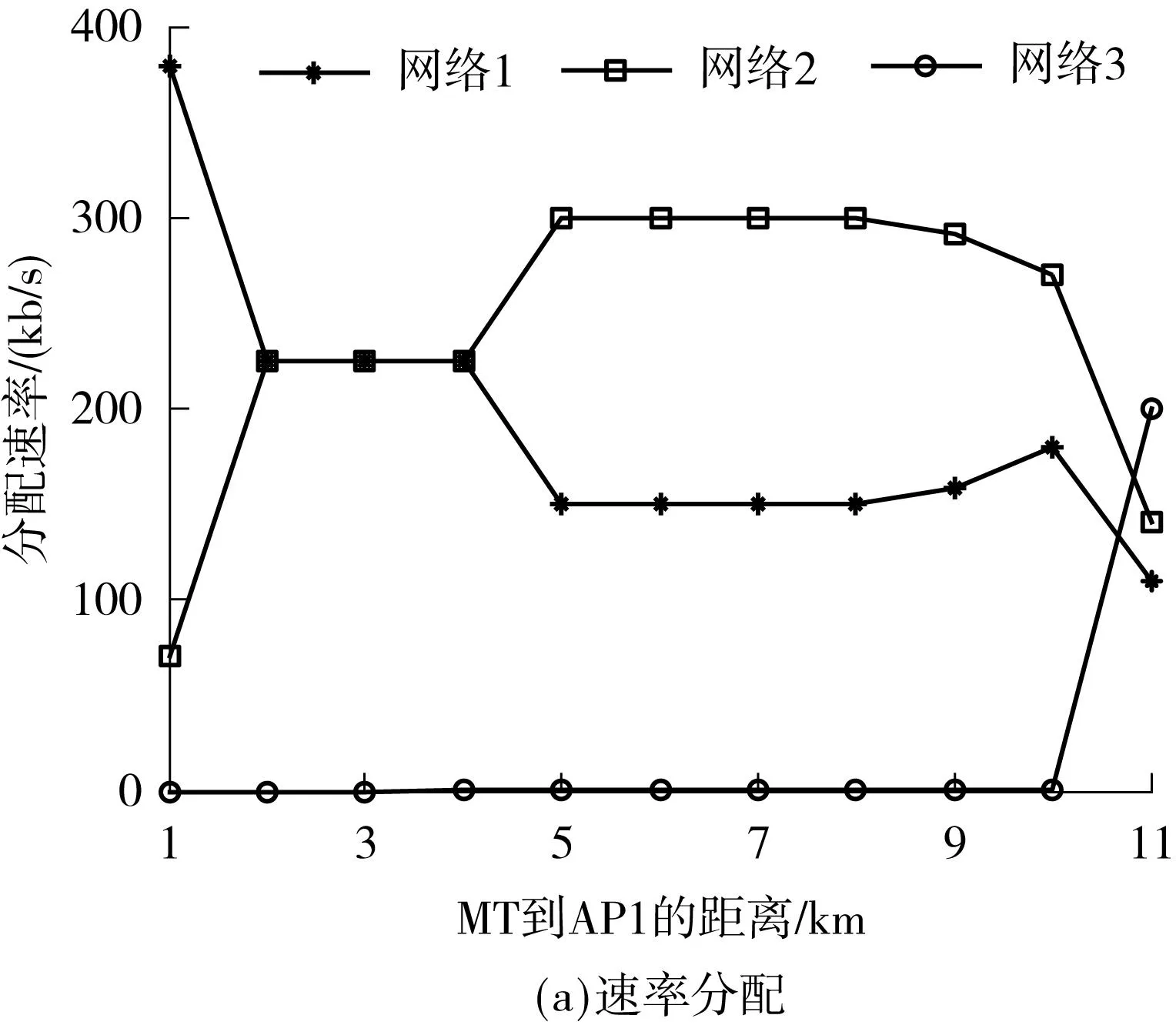
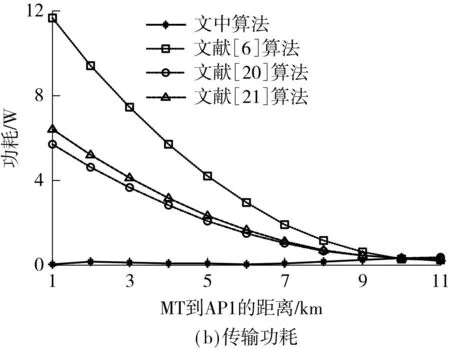
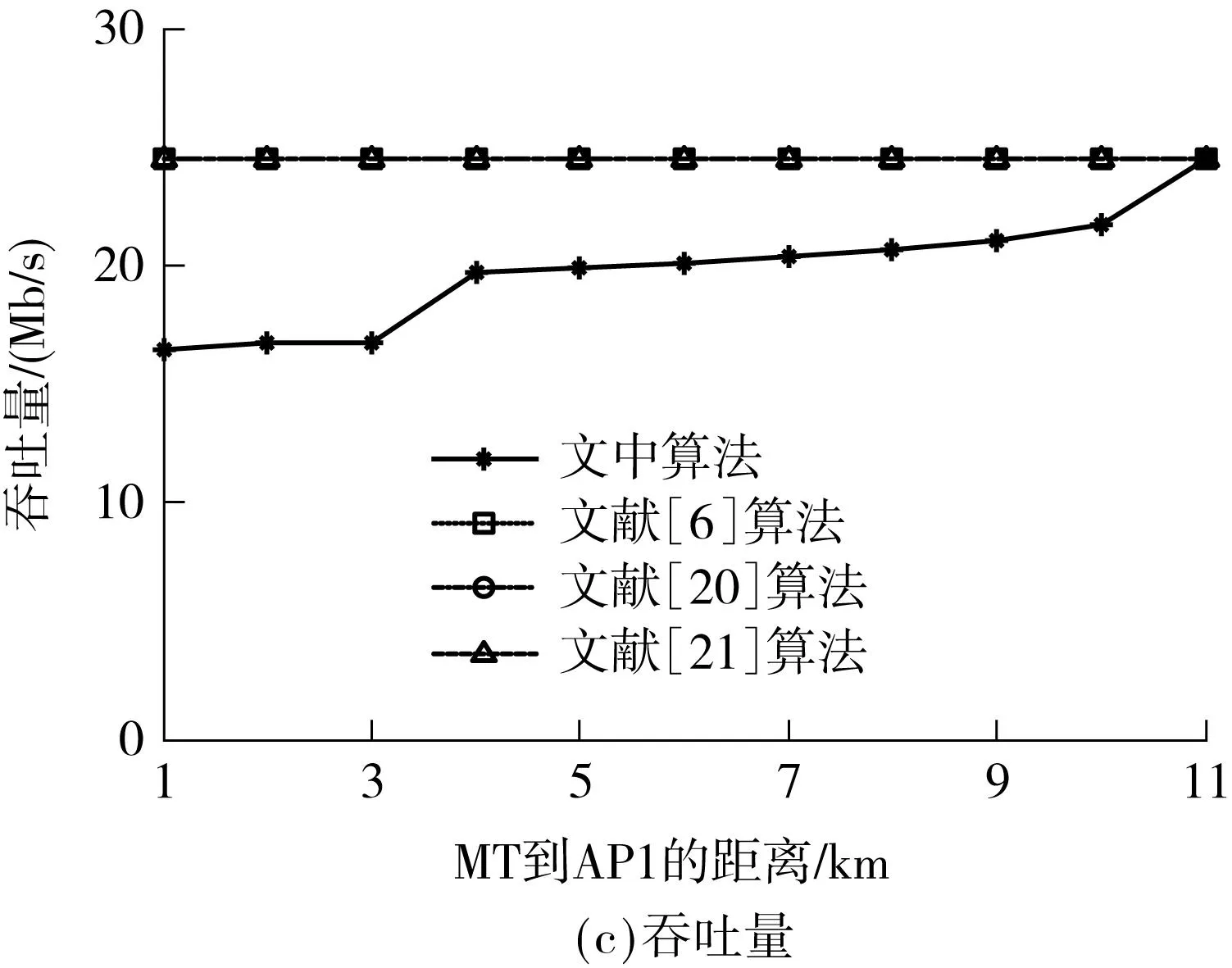
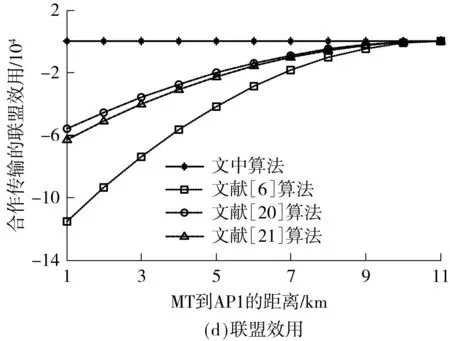
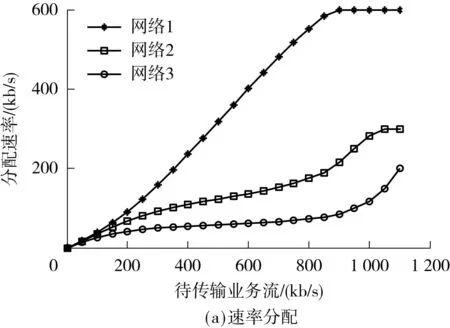
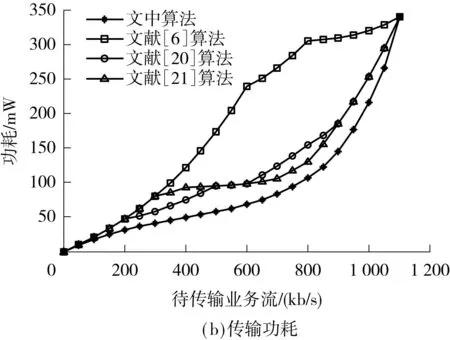
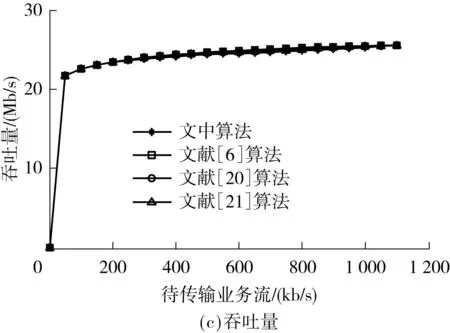
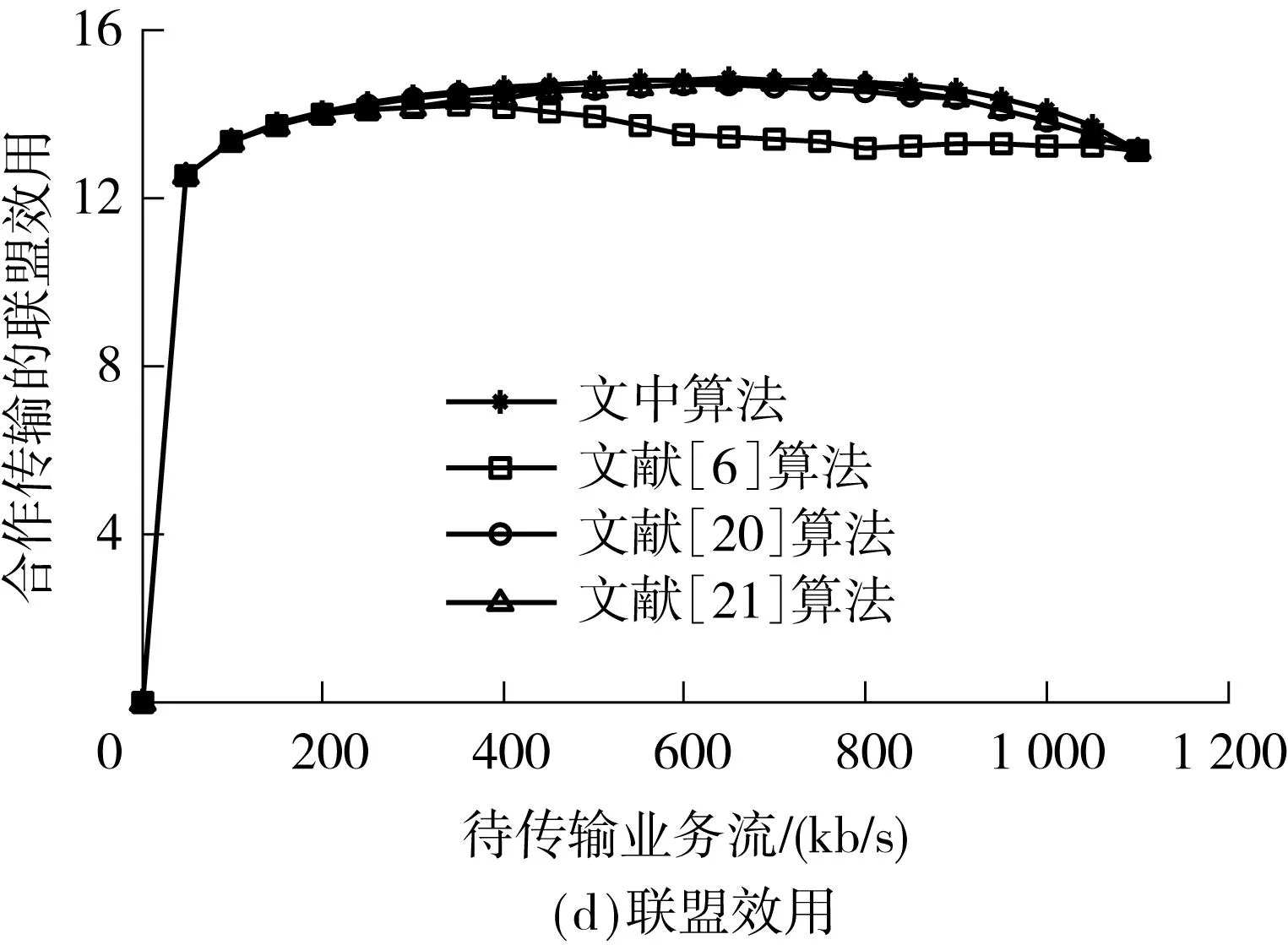
假设两个网络的接入点AP1、AP2相距很远,它们独自构成两个不相交联盟,即G1,G2⊂K′.MT通过较远接入点的传输功耗很大,甚至抵消其吞吐量收益,导致v(G1∪G2)=0 动态联盟形成可采用融合-分裂原则实现[17].文献[18-19]提出了一种基于该原则建立联盟的无线传感器网络的传输路径选择算法.文中利用该原则来实现网络联盟的动态形成,具体如下: 可见,如果不影响其他参与者,通过融合或者分裂可以提高至少一个参与者的回报,则联盟会进行融合或者分裂.如果遵循帕累托准则,所有的参与者都会从融合或者分裂中获利.在本文的速率分配算法中,该准则反复实施直至最终的划分由不相交的联盟组成. 推理1在速率分配算法中,采用融合-分裂原则在集合K′上实现的划分G′是Dhp-稳定的. 证明当基于融合-分裂的算法结束后,G′中的网络就不会再通过融合-分裂原则离开所属联盟,故该划分G′是Dhp-稳定的. 推理2在速率分配算法中,采用融合-分裂原则在集合K′上实现的划分G′可能是Dc-稳定的. 假设联盟H是互不相容的,且H⊂K′,如果属于不同Gi∈G′的多个接入点AP彼此距离很远,则 因此,在特定条件下,Dc-稳定的两个条件可以同时得到满足,通过融合-分裂原则组成的划分是Dc-稳定的. 3收益分配机制 联盟形成之后,可采用不同方法把收益分配给每个参与者,如Shapley值、Nash协商解、核仁、核等.考虑到计算复杂度和公平性等因素,文中采用Shapley值[20]来描述收益分配结果: [v(G)-v(G-{i})] (13) 4仿真和结果分析 仿真场景如图1所示,当MT要传输业务流时,它将搜索可用网络信息并确定它们的可用带宽Ci.如果∑Ci>M,则MT和可用网络组成全联盟并尽力传输业务流;否则,各网络根据信道带宽、信道噪声、传输距离及联盟收益分配的Shapley值,采用融合-分裂算法形成稳定联盟,上述参数可以在接入初始阶段估算或者交换.然后,为了最大化联盟收益,通过求导方法可确定MT在不同网络的传输速率.这个基于融合-分裂的联盟形成和联盟内速率分配过程不断进行,直至业务流传输结束.因此,文中所提算法的单次计算复杂度和基于破产博弈Shapley解算法相似,随着联盟形成和联盟内速率分配的反复进行不断增大,实际的时间复杂度与场景的具体情况有关. 网络参数会随着时间变化,如当MT远离AP时,网络搜索和参数检测需要重置,联盟结构也须随之调整.故基于融合-分裂的联盟形成和联盟内速率分配过程也会不断进行,直至业务流传输结束. 图2(b)、2(c)表明,文中算法的传输功耗始终最少,吞吐量比其他算法略低.可见,以吞吐量为代价,文中算法可以以较低的传输功耗获得最大联盟收益,具体见图2(d). 图2 实验1的性能对比Fig.2 Performance comparison in experiment 1 假设3个网络的噪声功率普密度分别为-140、-135、-110dBm/Hz;β1/w1=β2/w2=0.01,且β3/w3=10,其他参数同实验1.在图1中,不同网络的AP排列在一条直线上,AP1和AP2之间的距离为6km,AP2和AP3之间的距离是5km.待传输业务流速率是450kb/s,MT沿直线移动,实验结果见图3.图3(a)表明,开始时MT离AP3较远,网络3从全联盟中分裂出来,不参与传输.随着MT的移动,它到AP1的距离从1km增大到11km,网络1的信道衰减逐渐增大,r1不断减小;相反,随着MT靠近AP2,r2将增大.当MT靠近AP3时,网络3会参与联盟而获取更多的联盟收益,故r3增大,r1和r2减小.可见,文中算法可根据终端位置调整联盟结构和速率分配. 图3(b)-3(d)表明,文中算法的传输功耗始终最小,联盟收益始终优于其他算法.相比之下,其他几种算法的联盟结构默认为全联盟,终端位置和信道衰减的变化没有考虑,速率分配结果始终不变,故网络吞吐量不变.当MT到AP1的距离为1km时,它离AP3最远,全联盟导致通过网络3的传输功耗最大,结果整个联盟的收益最低. 图3 实验2的性能对比Fig.3 Performance comparison in experiment 2 5结论 由于数据传输功耗会抵消吞吐量收益,故全联盟不总是最优.为此,文中用联盟形成博弈论对速率分配进行建模,提出了一种动态的速率分配算法,该算法根据终端位置、传输需求可在终端采用分布式方法实现.实验结果表明,Nash协商解是文中算法的一个特例,它以吞吐量为代价可以在低功耗下获取最大联盟收益. 参考文献: [1]盛洁,唐良瑞,郝建红.异构无线网络中基于业务转移和接入控制的混合负载均衡 [J].电子学报,2013,41(2):321-328. ShengJie,TangLiang-rui,HaoJian-hong.Hybridloadbalancingalgorithmbasedonservicetransformationandadmissioncontrolinheterogeneouswirelessnetworks[J].ActaElectronicaSinica,2013,41(2):321-328. [2]姜建,李建东,刘鑫一.异构无线网络环境下的联合网络选择策略 [J].计算机学报,2014,37(2):407- 413. JiangJian,LiJian-dong,LiuXin-yi.Jointnetworkselectionstrategyinheterogeneouswirelessnetworks[J].ChineseJournalofComputers,2014,37(2):407- 413. [3]ZhuX,AgrawalP,SinghJ,etal.Distributedrateallocationpoliciesformultihomedvideostreamingoverheterogeneousaccessnetworks[J].IEEETransactionsonMultimedia,2009,11(4):752-764. [4]ArgyriouA,KosmanosD,TassiulasL.Jointtime-domainresourcepartitioning,rateallocation,andvideoqualityadaptationinheterogeneouscellularnetworks[J].IEEETransactionsonMultimedia,2015,17(5):736-745. [5]FanJin,RongZhang,LajosHanzo.Resourceallocationunderdelay-guaranteeconstraintsforheterogeneousvisible-lightandRFfemtocell[J].IEEETransactionsonWirelessCommunications,2015,14(2):1020-1034. [6]YaicheH,MazumdarR.Agametheoreticframeworkforbandwidthallocationandpricinginbroad-bandnetworks[J].IEEE/ACMTransactionsonNetworking,2000,8(5):667- 678. [7]NiyatoD,HossainE.Anoncooperativegame-theoreticframeworkforradioresourcemanagementin4Gheterogeneouswirelessaccessneworks[J].IEEETransactionsonMobileComputing,2008,7(3):332-345. [8]JayaweeraS,BkassinyM,AveryK.Symmetriccooperativecommunicationsbasedspectrumleasingviaauctionsincognitiveradionetworks[J].IEEETransactionsonWirelessCommunications,2011,10(8):2716-2724. [9]LiuJ,WeiG,WangY.Game-theoreticrateallocationwithbalancedtrafficincollaborativetransmissionoverheterogeneouswirelessaccessnetworks[J].IETCommunications,2012,6(10):1245-1251. [10]刘娇蛟,韦岗.基于加权协商对策论异构网络快速无线传输的速率分配算法 [J].电子学报,2012,40(7): 1471-1475. LiuJiao-jiao,WeiGang.Agame-theoreticrateallocationwithminimizedtransmissiontimeoverheterogeneouswirelessaccessnetworks[J].ActaElectronicaSinica, 2012,40(7):1471-1475. [11]SemasingheP,HossainE,KunZhu.Anevolutionarygamefordistributedresourceallocationinself-organizingsmallcells[J].IEEETransactionsonMobileComputing,2015,14(2):274-287. [12]BasarT,SrikantR.Revenue-maximizingpricingandcapacityexpansioninamany-usersregime[C]∥Procee-dingsofIEEEINFOCOM′02.NewYork:IEEE,2002:1556-1563. [13]MuthooA.Bargainingtheorywithapplications[M].Cambridge:CambridgeUniversityPress,1999. [14]RayD.Agame-theoreticperspectiveoncoalitionformation[M].NewYork:OxfordUniversityPress,2007. [15]AptKR,RadzikT.Stablepartitionsincoalitionalgames[EB/OL].(2006-05-29)[2014-10-28].http:∥arxiv.org/abs/cs.GT/0605132. [16]AptK,RadzikT.Agenericapproachtocoalitionformation(extendedversion) [J].InternationalGameTheoryReview,2009,11:347-367. [17]SaadWHZ,DebbahM,HjorungnesA.Adistributedcoalitionformationframeworkforfairusercooperationinwirelessnetworks[J].IEEETransactionsonWirelessCommunication,2009,8(9):4580- 4593. [18]LiuJJ,WangYG,WeiG.Distributedtopologycontrolbasedoncoalitionformationgameinwirelessnetworks[J].ComputerJournal,2013,56(8):968-976. [19]WuD,CaiY,WangJ.Acoalitionformationframeworkfortransmissionschemeselectioninwirelesssensornetworks[J].IEEETransactionsonVehicularTechnology,2011,60(6):2620-2630. [20]ShapleyLS.AvalueforN-persongame[J].AnnalsofMathematicsStudies,1953,2:307-317. [21]SchmeidlerD.Thenucleolusofacharacteristicfunctiongame[J].SIAMJournalofAppliedMathematics,1969, 17:1163-1170. Dynamic Rate Allocation of Heterogeneous Wireless Transmission Based on Coalition Formation Game Theory LiuJiao-jiaoMaBi-yun (School of Electronic and Information Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China) Abstract:Aiming at the rate allocation problem of the collaborative transmission in heterogeneous wireless networks, this paper introduces the transmission power cost into the coalition utility function, establishes a stable coalition on the basis of the merge-and-split rule and performs the dynamic rate allocation modeling on the basis of the coalition formation game theory. Then, a dynamic rate allocation algorithm is proposed. In order to maximize the coalition gain, the transmission rates in different networks are obtained through derivation. The above-mentioned process, which includes the merge-and-split-based coalition formation and the rate allocation in the coalition, continues until the end of traffic transmission. Simulation results demonstrate that the proposed algorithm can adjust the coalition structure dynamically in the transmission according to the terminal position and achieve a high coalition gain with a low power cost. Key words:collaborative transmission; rate allocation; game theory; Shapley value 中图分类号:TN929.5 doi:10.3969/j.issn.1000-565X.2015.09.005 作者简介:刘娇蛟(1976-),女,副教授,主要从事无线接入、协作通信研究.E-mail: jjliu@scut.edu.cn *基金项目:国家自然科学基金资助项目(61302056,61401158);广东省自然科学基金资助项目(S2013040016416);华南理工大学中央高校基本科研业务费专项资金资助项目(2014ZM0040);广州市科技计划项目(2012J2200005) 收稿日期:2014-11-03 文章编号:1000-565X(2015)09-0027-07 Foundation items: Supported by the National Natural Science Foundation of China(61302056,61401158) and the Natural Science Foundation of Guangdong Province(S2013040016416)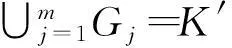
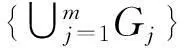

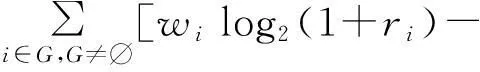
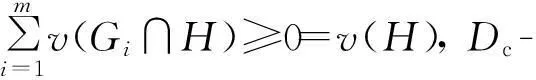
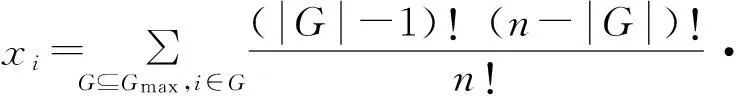

4.1 仿真实验1
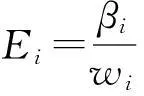
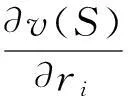
4.2 仿真实验2