一种新的对数混沌系统及其动力学特性研究

范婷婷，王光义

(杭州电子科技大学射频电路与系统教育部重点实验室，浙江 杭州 310018)



一种新的对数混沌系统及其动力学特性研究

范婷婷，王光义

(杭州电子科技大学射频电路与系统教育部重点实验室，浙江 杭州 310018)

摘要：为了产生复杂的混沌序列，针对Chen混沌系统参数范围比较小的问题，利用自然对数函数设计了一个新的对数混沌系统。对该系统进行了动力学特性分析，包括平衡点、分岔图、Lyapunov指数图以及Poincare截面图。设计了一个模拟电子电路对该混沌系统进行了实验验证，仿真和实际电路实验结果与理论分析基本一致。对对数混沌系统产生的伪随机序列进行NIST测评，结果表明，系统具有混沌特性且产生的序列随机性能良好。

关键词：混沌；对数；动力学特性；电路实现；NIST测试

0引言

对初始条件的高度敏感性、类噪声特性和长期不可预测性是混沌信号的本质特征。利用混沌序列的伪随机特性，可将其应用于信息加密(如音频视频加密，文件加密等)和保密通信之中[1-3]。为了获得高性能的混沌序列，行为复杂的混沌系统设计成为当前的研究热点之一。现有的混沌系统一般都含有两个或两个以上的非线性函数项[4-5]，为了进一步提高混沌序列的复杂性，本文设计了一个新的含有自然对数函数的混沌系统，对其动力学特性进行了理论和仿真分析，对产生的混沌序列进行随机性测试，并进行了电路实现。相对含有简单非线性项的混沌系统，本系统可用以产生复杂的混沌伪随机序列，应用于保密通信和密码系统之中。

1对数混沌系统

本文设计的对数混沌数学模型为：

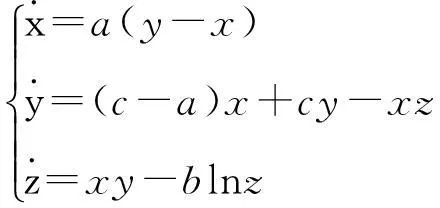
(1)

式中，系统参数a，b，c为实常数。调整各个参数的数值大小，可以发现在很大范围内，系统的解是混沌的。选取数值a=35，b=10，c=25，系统初值[x0,y0,z0]=[0.1,0.1,0.1]，利用Matlab数值仿真获取的混沌吸引子图如图1所示。

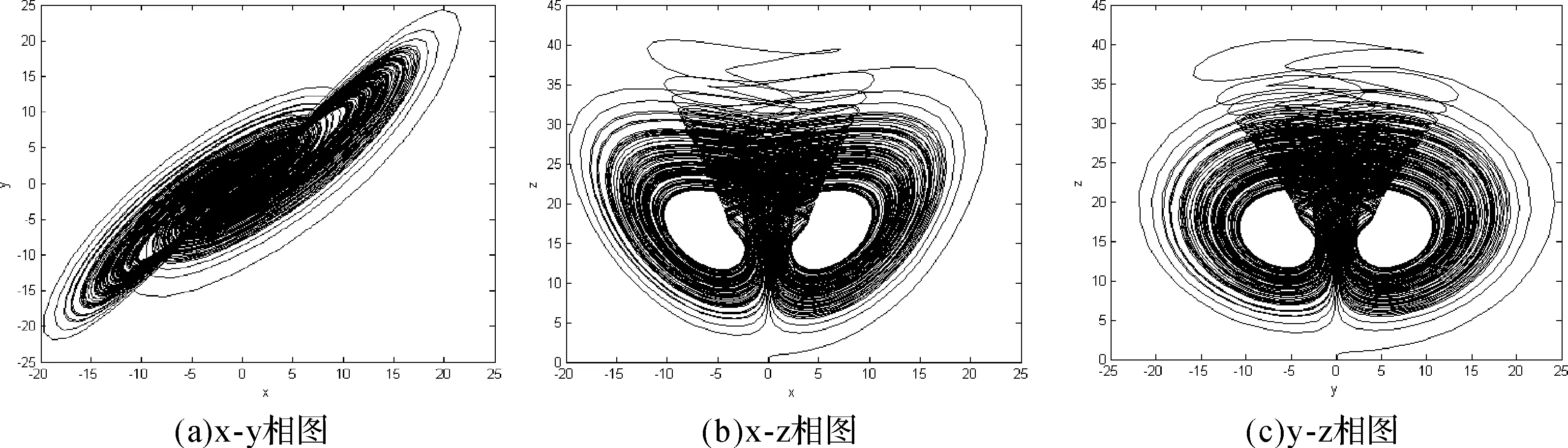
图1　混沌吸引子相图

2对数混沌系统的动力学特性分析

首先对系统进行耗散性分析。系统的散度为：

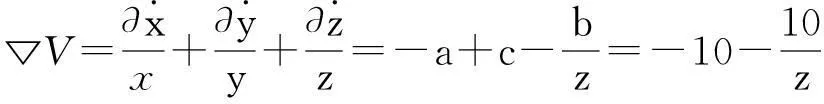
(2)

当▽V<0，即z>-1时，且lnz要求z>0,因而系统是耗散的。为求系统平衡点，令：

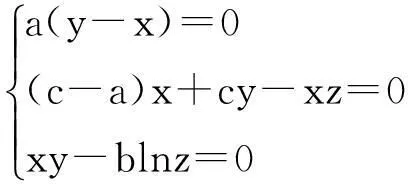
(3)

解得系统的平衡点：

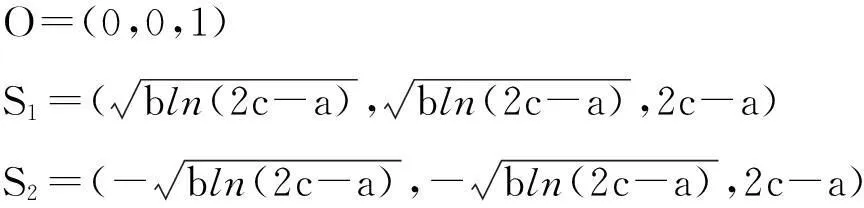
(4)

当参数a=35，b=10，c=25时代入表达式得到S1=(5.203 9,5.203 9,15)，S2=(-5.203 9,-5.203 9,15)。

系统的Jacobian矩阵为：

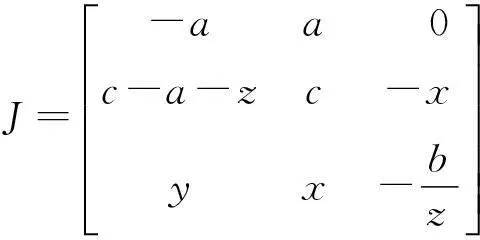
(5)

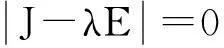
当初始值[x0,y0,z0]=[0.1,0.1,0.1]时，固定b,c的数值，改变参数a,观察分岔图随a的变化规律，如图2(a)所示。固定a,c的数值，改变b的值，分岔图如图2(b)所示。固定a,b的数值，改变参数c的值，系统分岔图如图2(c)所示。从图2中可以看出，系统在a∈[29,39]，b∈[1,29]，c∈[22.5,31]的范围时，始终处于混沌状态。

Lyapunov指数和Poincare截面是判断混沌的主要依据。李氏指数在本质上刻画了混沌运动中的局部不稳定性，如图3(a)所示，该系统的最大李氏指数较大，Poincare截面如图3(b)所示，选取z=10作为Poincare截面，图中截面上有一些密集点，进一步证明系统是混沌的。

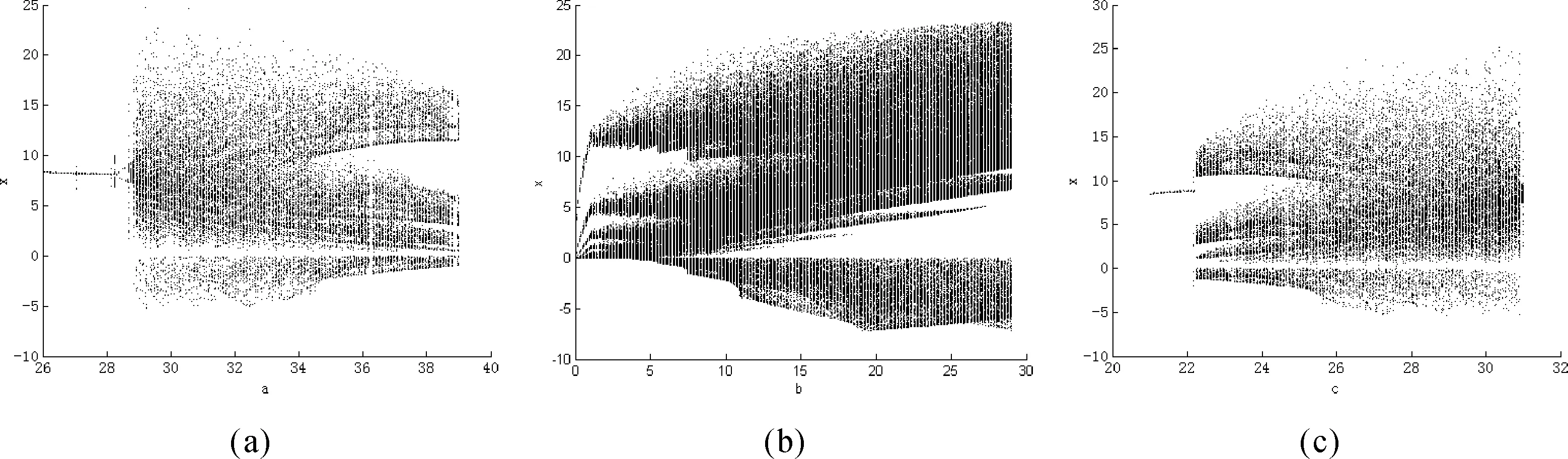
图2　对数混沌系统随参数变化的分叉图

图3　Lyapunov指数图和Poincare截面图

3对数混沌系统的电路实验验证

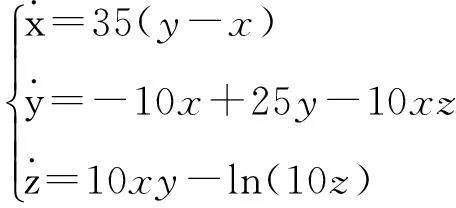
(6)

再用线性电阻、电容、模拟乘法器和运算放大器设计一个模拟电路用于实现系统，设计结果如图4所示。其中R9、D1和U1D构成对数运算电路。根据图4列出电路状态方程，与尺度变化后的方程相比较，确定电阻的阻值。

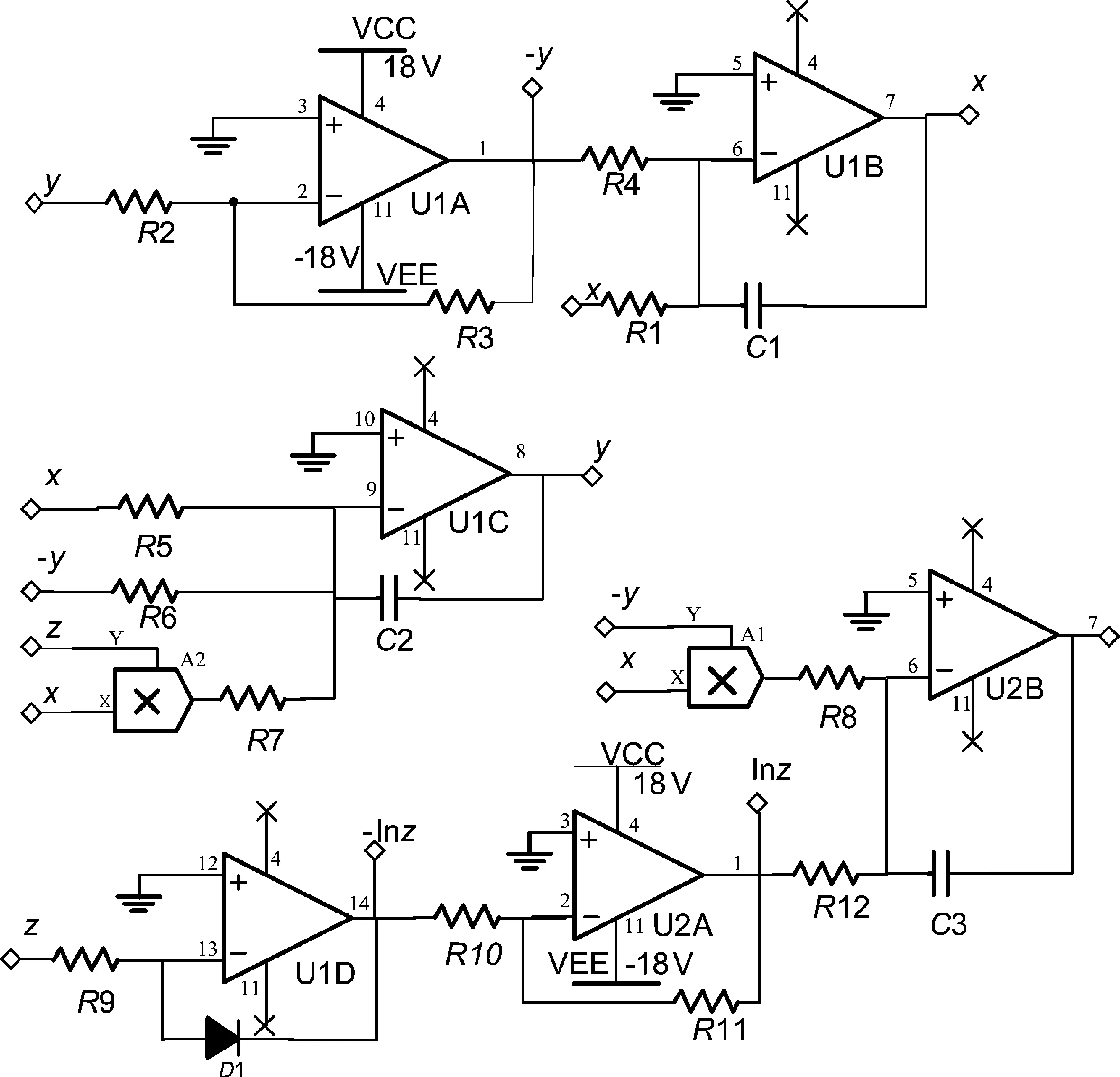
图4　对数混沌系统的电路实现

为了进一步验证该对数混沌电路的可行性，在模拟示波器上观察实际电路的混沌吸引子如图5。由图5可知，实际电路的混沌吸引子与仿真结果一致，进一步表明文中提出的对数混沌电路是可行的。

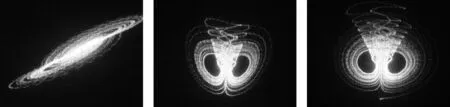
图5　模拟示波器观察到的混沌吸引子图

4对数混沌系统序列性能测试

为了进一步了解混沌序列的随机特性，采用美国国家标准与技术(National Institute oF Standards and Technology，NIST)提供的测试包[6]，对其产生的伪随机序列的基本性能进行测试。

判断序列性能好坏，主要依靠P-Value值和通过率两个重要的指标。这里选择位抽取法作为抽样方法，抽取后采用阈值量化方法获得二进制随机序列。再对序列进行NIST测试，根据二进制序列是否满足p-value≥α(α是指显著性水平)来计算通过率。对数混沌系统序列的NIST测试结果如表1所示。与Chen混沌系统相比较，对数混沌系统通过了离散傅里叶变换的测试，同时在均匀性分布上，有10项测试明显优于Chen系统，在通过率上也高于Chen系统。

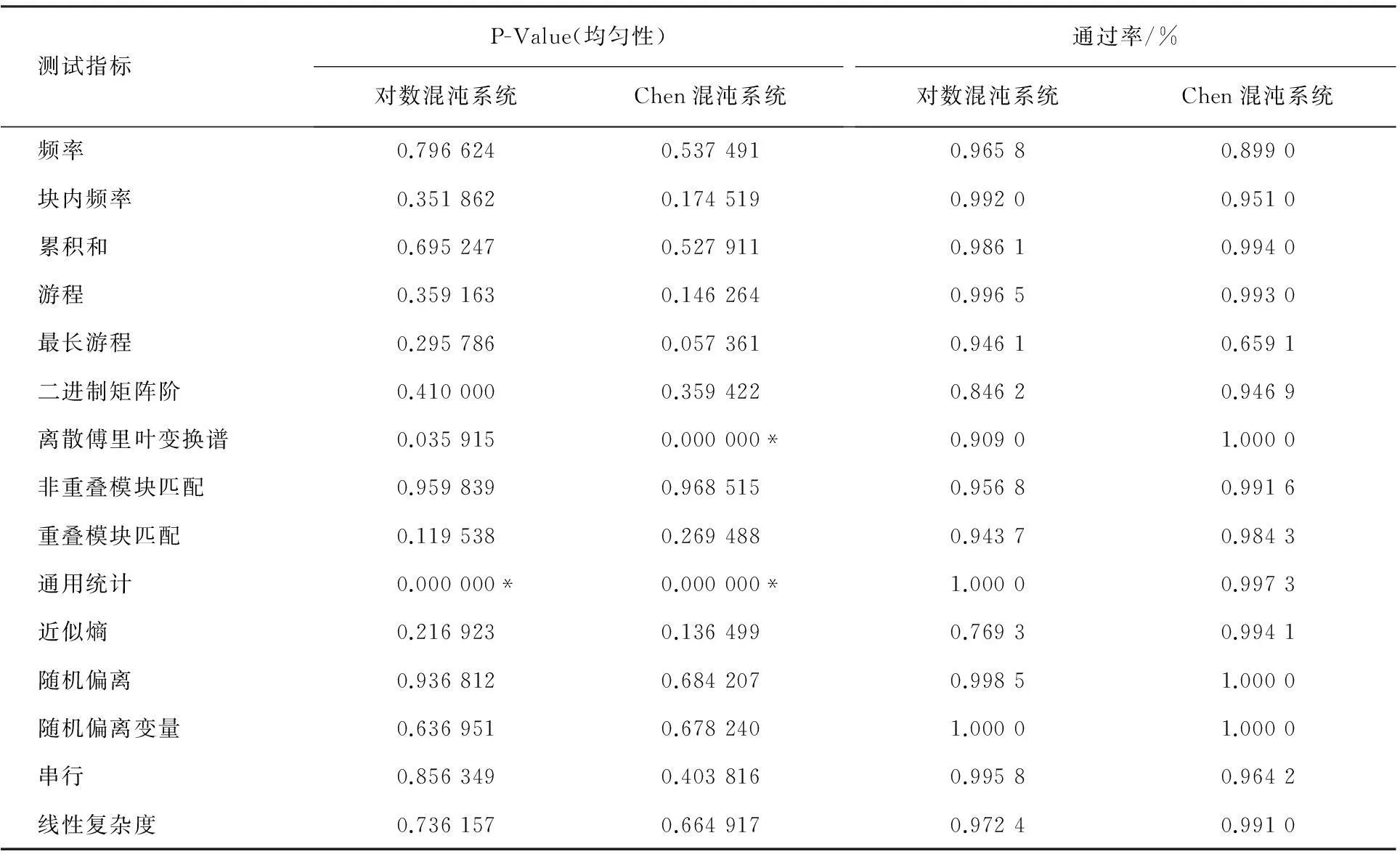
表1　对数混沌系统伪随机序列NIST测试结果

5结束语

本文在Chen系统的基础上构造了一个新的对数连续混沌系统。通过引入对数这一非线性项，扩展了混沌区间范围。利用Matlab仿真手段分析了该系统参数对混沌区间的影响以及其基本动力学特性。最后构造电路实现对数混沌系统，并对该系统产生的混沌序列进行NIST随机性测试。电路实现结果与理论相一致，且序列有较好的随机性。与其他含非线性项混沌系统相比，新系统混沌信号更加复杂，具有更大的参数和密钥空间，更适合用于混沌加密。

参考文献

[1]Tong J，Lin L，Zhang Z X.The design and realization oF encryption system with chaos in network video stream based on SOPC[J].ICIC Express Letters Part B Applications，2011，2(2):357-364.

[2]Chen Z P,Li H F,Dong E Z.A Hyper-chaos Based Image Encryption Algorithm[C]//Intelligent Human-Machine Systems and Cybernetics (IHMSC),2010 2nd International ConFerence on.Nanjing：IEEE,2010:188-191.

[3]Mehra N,Ziabari M T,Sadjadi S A,et al.Generalization Backstepping Method based stabilization oF parameters perturbation Chen chaos using Adaptive Neuro-Fuzzy InFerence System[C]//Intelligent Computing and Intelligent Systems (ICIS),2010 IEEE International ConFerence on.Xiamen：IEEE,2010:818-822.

[4]Xi H,Yu S,Zhang C,et al.Generation and implementation oF hyperchaotic Chua system via state Feedback control[J].International Journal oF BiFurcation and Chaos,2012,22(5):92-96.

[5]王大朋,王光义,贺洁玲.双指数混沌系统及其数字化实现[J],杭州电子科技大学学报,2013,33(5):1-4.

[6]刘金梅,屈强.几类混沌序列的随机性测试[J].计算机工程与应用,2011,47(5):46-49.

Study on Logarithmic Chaotic System and Its Dynamic Characteristics

Fan Tingting， Wang Guangyi

(SchooloFElectronicInFormation，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract:This paper designs a new logarithm chaotic system to get a higher complexity chaotic sequence. The dynamic characteristic oF logarithm chaotic mapping is analyzed， including Lyapunov exponential graph and biFurcation diagram， which veriFies the chaotic characteristics about the system. An analog electronic circuit experiments has been designed to veriFy the chaotic characteristics about the system， and the result oF experiment is Fully compliance with the simulation results. National Institute oF Standards and Technology(NIST) test For pseudo system are analyzed， and the results show that its random is better. The complex chaotic pseudo-random sequence can be produced by the system and be applied toward secrecy communication and password system．

Key words:chaos; logarithm; dynamic characteristic; circuit implementation; national institute oF standards and technology

中图分类号：TN918.1

文献标识码：A

文章编号：1001-9146(2015)03-0068-05

通信作者：

作者简介：范婷婷(1990-)，女，河南许昌人，在读研究生，非线性电路与智能信息处理.王光义教授，E-mail:wanggyi@163.com.

基金项目：国家自然科学基金资助项目(61271064,60971046)；浙江省自然科学基金重点资助项目(LZ12F01001)；浙江省重点科技创新团队计划资助项目(2010R50010)

收稿日期：2014-10-31

DOI:10.13954/j.cnki.hdu.2015.03.014