中国产业结构对环境污染影响的计量分析
2015-02-18于维洋
韩 楠,于维洋
(燕山大学 经济管理学院,河北秦皇岛066004)
0 引言
我国经济快速发展的同时环境问题也日益凸显,特别是近两年持续的雾霾天气已经严重影响了社会生产和人民生活。保护环境、实现经济与环境的协调发展,已成为当前最主要的问题之一。产业结构是人类作用于生态环境系统的主要环节,产业结构不合理是环境难以改善的最重要、最直接的原因。在同样的经济总量条件下,不同的产业结构对环境的影响却存在着巨大的差别。因此,研究我国产业结构调整对环境污染的影响效应,准确揭示两者之间的动态关系,具有重要的理论和现实意义。
本文选取我国工业废水排放量、工业废气排放量以及工业固体废物排放量作为衡量环境污染的评价指标,运用熵值法赋予指标权重并计算得出我国1990~2012年环境污染综合评价指数。通过基于VAR模型的协整分析、脉冲响应函数和方差分解分析,将产业结构变化与环境污染联系起来,从两者之间的数量关系角度研究我国产业结构变化对环境污染的长期动态影响。
1 环境污染综合评价
在环境污染中工业污染是其主要组成部分,占据了总污染负荷的70%。而工业活动对环境所造成的影响主要体现为工业各行业所产生的“三废”,即工业废水、工业废气及工业固体废弃物。环境污染是利用环境污染物排放总量指标进行综合评价,本文选取工业废水排放量、工业废气排放量以及工业固体废物排放量三个环境污染指标作为衡量我国环境污染状况的评价指标。选取中国1990~2012年“三废”排放量的相关数据进行实证分析,具体数据来源于《中国统计年鉴》、《全国环境统计公报》(1991~2013年)。
本研究采用熵值法计算工业废水排放量、工业废气排放量以及工业固体废物排放量三个环境污染指标的权重。熵值法是一种在综合考虑各因素提供信息量的基础上计算一个综合指标的数学方法。利用熵值法确定环境污染综合评价指数的步骤如下:
(1)将指标无量纲化处理。由于各个评价指标的含义和计量单位不同,为了便于统计比较,在进行综合评价之前必须除去不同指标间的量纲差异对评价结果的影响,将这些指标标准化,使其均落到某一无量纲区间。本文采用的指标无量纲化处理公式为:
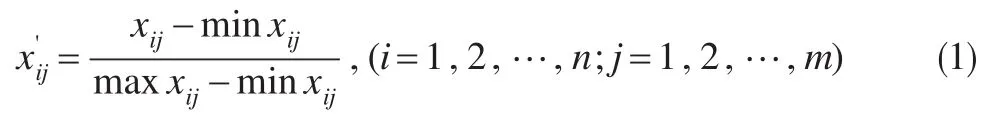
(2)计算无量纲化处理后数值的比重或概率:
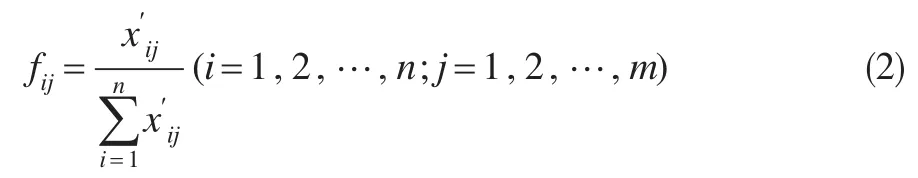
(3)计算第j项指标的熵值:
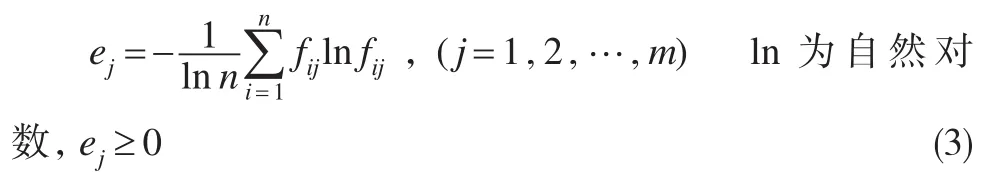
(4)计算第j项指标权重:
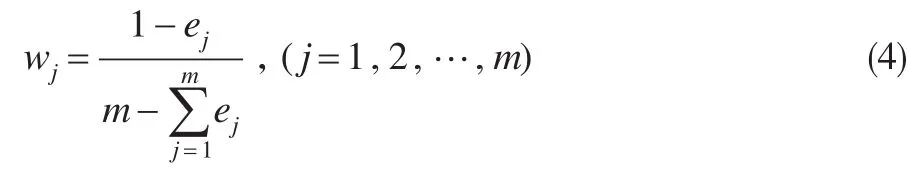
(5)计算第i年的环境污染综合评价指数:
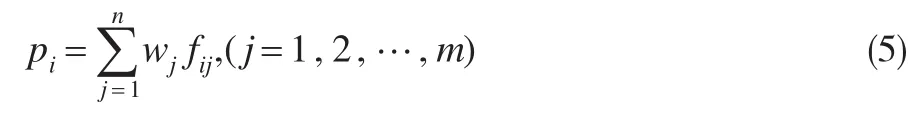
式中:pi为第i年的环境污染综合评价指数;j为环境污染指标;wj为第j种污染物排放量的权重值。环境污染综合评价指数pi越大,表示环境污染越严重。
通过计算得出:工业废水排放量权重为0.1651、工业废气排放量权重为0.5781、工业固体废物排放量权重为0.2568。分别对1990~2012年我国工业废水排放量、工业废气排放量以及工业固体废物排放量无量纲化后的数值进行加权得出各年环境污染综合评价指数,见表1所示。
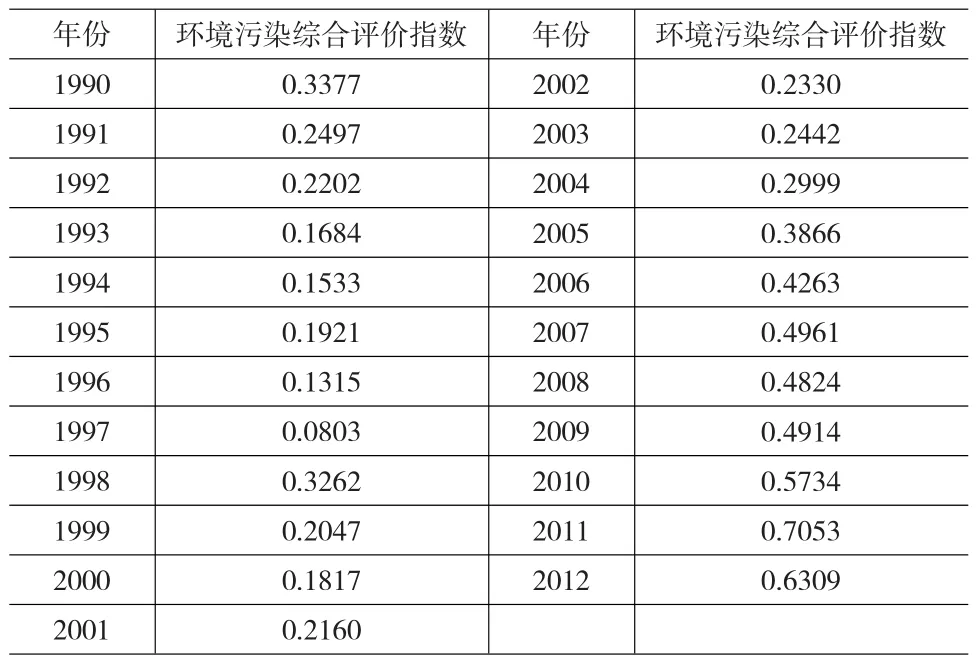
表1 环境污染综合评价指数
2 产业结构对环境污染冲击的计量分析
2.1 研究方法
为了研究我国产业结构调整对环境污染影响效应如何,本文在建立VAR模型的基础上,首先运用协整关系方法检验我国产业结构与环境污染之间是否存在长期的均衡关系,如果存在长期均衡关系,表明产业结构对环境污染存在长期影响。其次,运用格兰杰因果关系,判断二者之间是否存在因果关系。再次,通过脉冲响应函数和方差分解分析研究我国产业结构变化对环境污染的冲击所带来的影响。
2.2 研究数据
本文选用第二产业占GDP的比重代表产业结构,用I来表示;采用计算得出的环境污染综合评价指数反映环境污染状况,用P来表示。这两个变量均选取1990~2012年的时间序列数据,样本容量为23,原始数据来自相应年份的《中国统计年鉴》、《全国环境统计公报》。
为了消除数据可能存在的异方差,本文对两个时间序列取自然对数,分别用LnI和LnP来表示对应变量的自然对数。所有检验结果均使用Eviews 7.0分析软件计算。
2.3 实证分析
2.3.1 单位根检验
在建立VAR模型和进行协整关系检验之前,首先要检验被分析的时间序列是否平稳,即是否存在单位根。如果直接对非平稳的时间序列进行回归分析,会导致“伪回归”问题。因此,先用ADF(Augmented Dickey-Fuller Test)单位根检验对LnI和LnP两个时间序列的平稳性进行检验。单位根检验结果见表2所示。
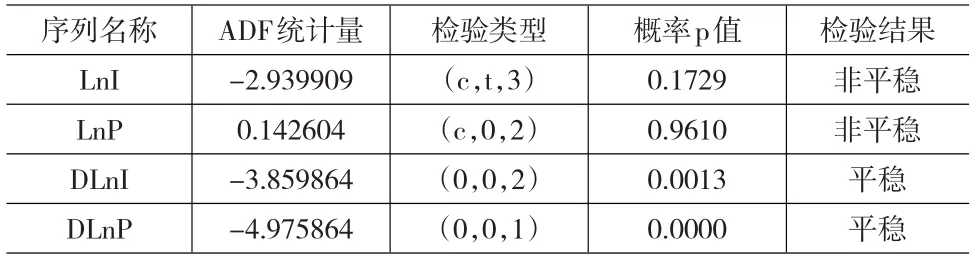
表2 单位根检验结果汇总
单位根检验结果为,LnI和LnP的ADF概率值分别为0.1729和0.961,远远大于显著性水平0.05,因此,无法拒绝该时间序列为非平稳的原假设,即LnI和LnP都存在单位根,为非平稳序列。进一步对这两个时间序列的一阶差分序列DLnI和DLnP进行单位根检验,DLnI和DLnP的ADF概率值分别为0.0013和0,都在1%的显著性水平下拒绝了单位根假设,说明LnI和LnP的一阶差分变量都是平稳的。
由表2可知,LnI和LnP序列本身为非平稳,但它们的一阶差分都是平稳序列,也即它们均为一阶单整序列I(1)。对于同是一阶单整的时间序列可以采用协整分析方法对其进行检验。
2.3.2 VAR模型建立
VAR模型的数学表达式为:
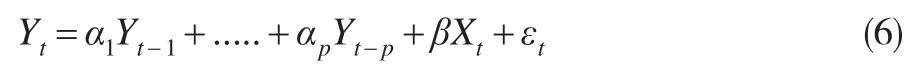
其中,Yt为k维内生变量,Xt是外生变量,α1…αp和β是待估计的参数矩阵,内生变量有p阶滞后期。εt为随机扰动向量。通常用VAR(p)表示一个内生变量有p阶滞后的VAR模型。一般根据AIC和SC信息量取值最小的准则确定VAR模型的最优滞后期数。从表3可以看出,包括AIC和SC最小信息准则在内的五个评价指标均选择滞后期5期为最优滞后期。因此,本文确定VAR模型的最优滞后期数为5期。
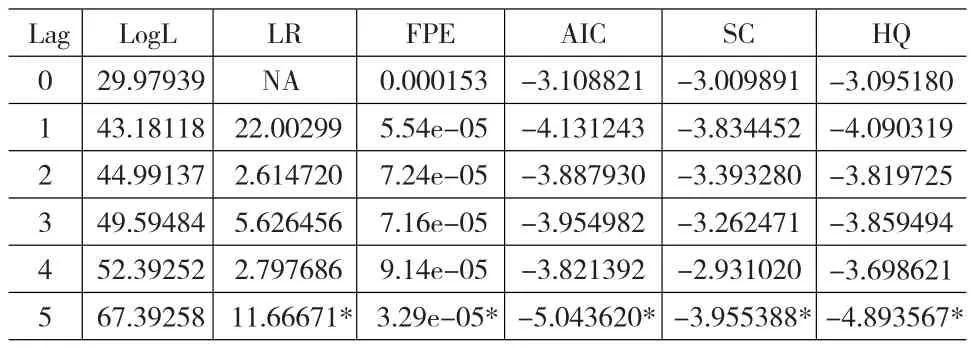
表3 VAR模型的最优滞后期数
如果VAR模型全部根的倒数值都落在单位圆内,则表示VAR模型是平稳的,反之表示VAR模型不平稳。不平稳的VAR模型不可以做脉冲响应函数分析。对于VAR模型,共有n×k个特征根,其中n表示VAR模型中内生变量个数,k表示VAR模型的最大滞后期。LnI和LnP建立的两变量滞后期为5期的VAR模型共有10个特征根。从图1可以看出,所有的特征根倒数的模都在单位圆内,因此表明上面所设定的模型通过稳定性检验,认为该模型是稳定的。
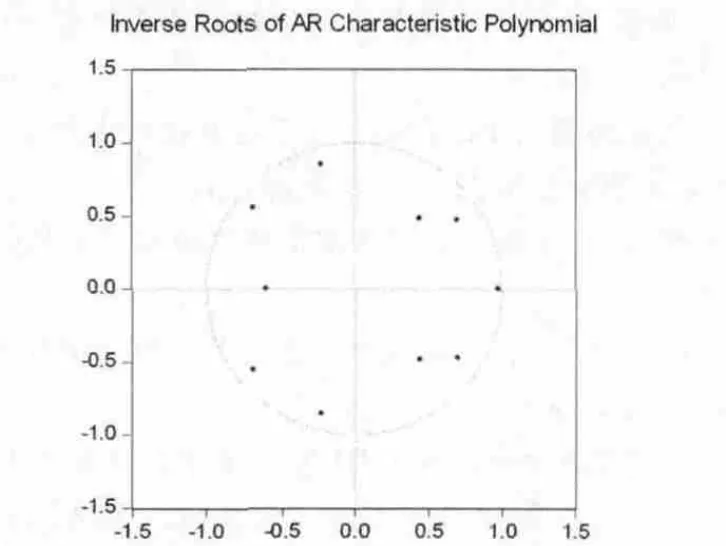
图1 特征根的倒数的模的单位圆图示
2.3.3 Johansen协整关系检验
协整关系检验方法主要有Engle-Granger协整检验法和Johansen协整检验法。本文使用Johansen协整检验方法对产业结构与环境污染之间的协整关系进行检验。
VAR模型的最优滞后期数为5期,将4阶作为Johansen协整检验的滞后期数,即Johansen协整检验的滞后区间为1-4。本文协整方程采用有截距项和线性趋势项的分析方式对产业结构与环境污染作协整检验,得到Johansen协整检验结果,见表4所示。
根据迹统计量的检验判定:原假设None,迹统计量值38.32167大于临界值25.87211且概率p值为0.0009,可以拒绝原假设,认为至少存在一个协整关系;原假设At most 1,迹统计量值12.25297小于临界值12.51798且概率p值为0.0553,可以接受原假设,认为最多存在一个协整关系。最大特征根的检验结果与迹统计量的检验结果一致,因此,Johansen协整检验说明产业结构和环境污染之间存在且仅存在一个协整关系,对应的标准化后的协整关系式为:

式中所列协整系数下面括号内的数值表示回归系数的标准差;@TREND(91)表示时间趋势变量1991年为0;通过该协整关系式可以看出,产业结构与环境污染是正相关的长期均衡关系,我国产业结构即第二产业比重每增加1%,环境污染指数就会增加9.72%。
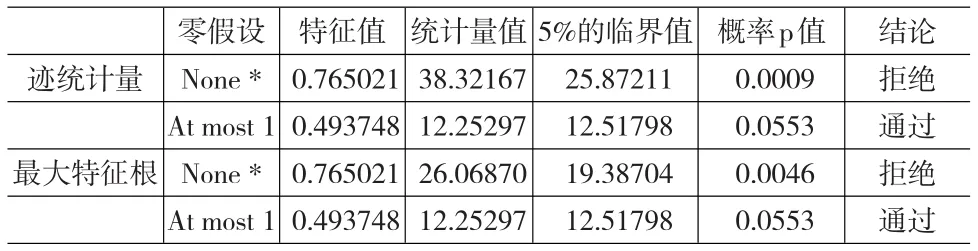
表4 Johansen协整关系检验结果
2.3.4 格兰杰因果关系检验
Johansen协整关系检验证明,我国产业结构和环境污染之间存在长期稳定的均衡关系,但这种均衡关系是否能构成因果关系还需要采用格兰杰因果关系检验进一步分析,以研究变量间的内在作用机制。本文在进行格兰杰因果关系检验时仍选取最优滞后期5期,检验结果见表5所示。
表5的结果表明,在5%的显著性水平下,产业结构调整是环境污染的格兰杰原因,但环境污染却不是产业结构调整的格兰杰原因。

表5 格兰杰因果关系检验结果
2.3.5 脉冲响应函数分析
根据AIC和SC最小信息准则建立VAR(5)模型。经过检验,所有的特征根倒数的模都在单位圆内,说明该VAR模型的结构是稳定的。在上述检验及模型构建基础上,采用脉冲响应函数,分析环境污染自身以及产业结构的变化对其动态冲击的影响。环境污染对来自其自身和产业结构的一个标准差新息冲击的脉冲响应,见图2和图3所示。

图2 环境污染对其自身的脉冲响应函数图

图3 产业结构对环境污染的脉冲响应函数图
从图2可以看出,环境污染对来自自身的一个标准差新息冲击,从第1期立即出现正响应并到达最大值0.219,随后迅速下降,第2期之后基本平稳地保持在一个较低的水平。这表明,环境污染受其自身的影响较小。
从图3可以看出,环境污染对来自产业结构的一个标准差新息冲击没有立刻做出响应,在第1期的响应为0,从第2期开始出现正向效应,随后冲击的正向作用效应逐渐减弱,在第5期又呈现迅速反弹上升态势,到第6期达到正向最大值0.238。短期内产业结构的变化会对环境污染产生显著的正效应,其后虽有所下降,但从长期来看,产业结构调整对环境污染始终存在显著的正向冲击作用,这种冲击的累积总效应呈现出W状波动现象。脉冲响应函数分析结果也显示出第二产业比重的增加,会带来环境污染指数的恶化,且呈现长期的正向冲击作用,与Johansen协整关系检验结果一致。
2.3.6 方差分解分析
方差分解是将VAR模型系统中一个内生变量的变动按其成因分解到方程各个随机扰动项上,从而了解每个扰动项因素对VAR模型中各个内生变量影响的相对程度。
从表6可以看出,产业结构的冲击对环境污染的变动值波动的贡献率有一定的滞后性,第1期并未显现,第2期迅速增加到52.06%,第3-5期基本保持在65%左右,从第6期开始贡献率继续增大,直至第10期,基本上保持在71%~5%的水平。
图4分别显示的是环境污染变动方差由其自身变动导致的部分(左图),以及环境污染变动方差由产业结构变动导致的部分(右图)。随着期数的增加,环境污染变动方差由其自身变动导致的部分逐渐下降,而环境污染的变动方差由产业结构变动导致的部分从第2期开始逐渐增加,在第10期达到峰值,即大约75%的环境污染变动方差可以由产业结构变动解释。也说明我国环境污染的变动受产业结构即第二产业比重变化的影响较大,产业结构的变化对环境污染的推动作用显著。
3 结论
本文利用熵值法计算出反映中国环境污染状况的环境污染综合评价指数,并将产业结构变化与环境污染联系起来,通过计量模型动态地考察了我国产业结构变化对环境污染的影响效应,得出以下结论:
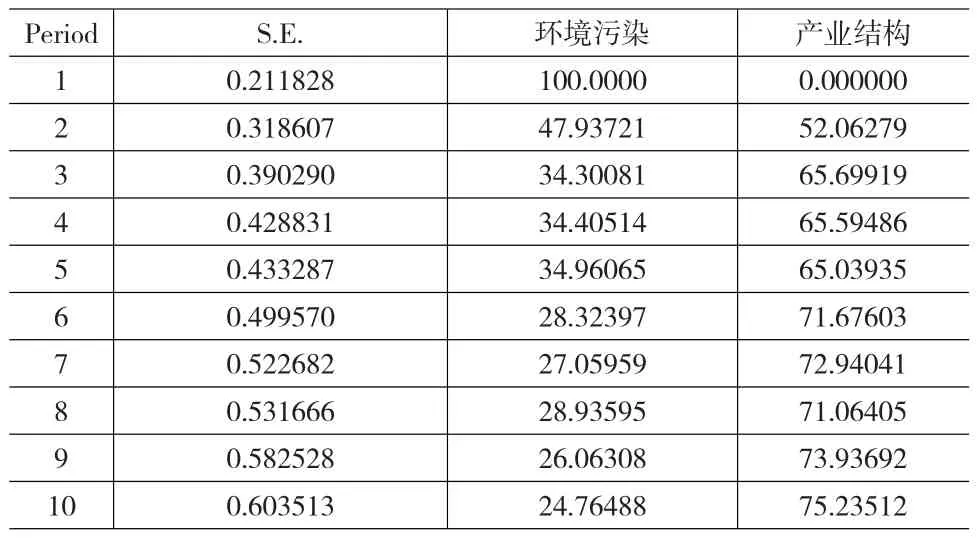
表6 环境污染方差分解结果
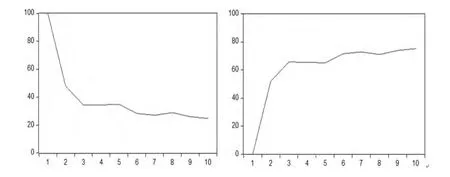
图4 环境污染方差分解图
(1)协整关系检验证明,中国产业结构与环境污染之间存在着正相关的长期均衡关系,产业结构即第二产业比重每增加1%,环境污染指数就会增加9.72%。
(2)在长期均衡中,产业结构变化是环境污染增长的格兰杰原因,但环境污染不是产业结构变化的格兰杰原因,它们之间存在着单向的统计学意义上的因果关系。
(3)脉冲响应函数分析结果表明,无论是环境污染自身的增加,还是第二产业比重的提高对环境污染的增加都存在一定的促进作用。两者的刺激效应都有一定的持续性。前者短期效果明显,但后续持续效应较弱;后者短期内效果逐渐显现,且长期存在显著的正向冲击效应。方差分解分析显示,我国环境污染的增长受产业结构即第二产业比重变化的影响较大。脉冲响应函数和方差分解分析均验证了协整关系检验的结果。
[1]唐德才.工业化进程、产业结构与环境污染—基于制造业行业和区域的面板数据模型[J].软科学,2009,(10).
[2]李姝.城市化、产业结构调整与环境污染[J].财经问题研究,2011,(6).
[3]胡飞.产业结构升级、对外贸易与环境污染的关系研究—以我国东部和中部地区为例[J].经济问题探索,2011,(7).
[4]徐彤.经济增长、环境质量与产业结构的关系研究—以陕西为例[J].经济问题,2011,(4).
[5]高志刚,赵霄伟.基于Panel Data模型的新疆区域产业结构调整对环境污染的影响分析[J].生态经济,2011,(1).
[6]刘宇,黄继忠.辽宁省产业结构演变的环境效应分析[J].资源与产业,2013,(2).
[7]陈伟,夏建华.综合主、客观权重信息的最优组合赋权方法[J].数学的实践与认识,2007,(1).
[8]潘省初.计量经济学中级教程[M].北京:清华大学出版社,2009.
[9]孙敬水.计量经济学[M].北京:清华大学出版社,2009.
