时间透镜成像系统的数值分析

郭淑琴，俞梦杰

(浙江工业大学 信息工程学院，浙江 杭州 310023)

时间透镜成像系统的数值分析

郭淑琴，俞梦杰

(浙江工业大学 信息工程学院，浙江 杭州 310023)

摘要：在高非线性光纤中利用四波混频(FWM)效应产生时间透镜，由输入色散光纤、时间透镜，以及输出色散光纤三部分构成光信号处理的时间成像系统.时间透镜将泵浦光的二次相位通过四波混频作用传递给信号光，啁啾化的信号光在经过光纤的色散之后可以引起脉宽的放大或压缩.数值计算表明：在时间成像系统中，采用较宽的泵浦光会导致信号光脉宽的放大倍数M值下降，但泵浦光输入功率的强弱对放大因子M值没有影响.考虑到光纤的损耗会导致色散线路上信号功率的衰减，为使色散与非线性效应动态匹配，将输入输出两段光纤的色散由固定值改进为指数渐减，可以使放大倍数更趋近于理论值.

关键词：时间透镜；FWM效应；时间成像系统；放大因子

中图分类号：O439

文献标志码：A

文章编号：1006-4303(2015)01-0094-03

Numerical study on the temporal imaging system based time lenses

GUO Shuqin, YU Mengjie

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:Based on four wave mixing effect(FWM effect) in high nonlinear optical fiber, a temporal imaging system is comprise of an initial fiber, time lens, and a final fiber for optical signal proceeding. Pump pulse transfers its quadratic phase to signal pulse through four wave mixing effect, and so chirped signal will be magnified or reduced after suffering proper dispersion in optical fiber. By numerical calculation, it can be seen that the wider pump pulse will induce magnification rate a little smaller than the theoretical value in the temporal imaging system, but pump power has no impact on magnification factor. Because the loss of fiber will attenuate the power of signal in propagating process, so when dispersion parameter is designed according to the exponential decreasing rule, perfect mapping between dispersion and nonlinear make the magnification factor more near to theoretical value.

Keywords:time lens；FWM effect；temporal imaging system；magnification factor

傍轴光束在自由空间的衍射与窄带时间信号在色散介质中的传输遵从类似的波动方程，人们将这种相似性归纳为光的时空“二元性”.利用光的“二元性”，将空间付里叶光学中的光学器件如“棱镜”、“透镜”等基本概念，以及成像理论都对应地引入到时间域中，形成“时间棱镜”、“时间透镜”概念，以及时间成像理论，从而构建全光信号处理系统，实现时间信号的放大、压缩，以及时频变换.时间成像技术将在高速的信号源与低速的测量设备之间架起一座桥梁，能够对超短超快信号实时捕捉.“时间透镜”的概念由Kolner和Nazarathy[1]于1989年首次提出，类似于空间透镜，“时间透镜”能够对穿过的光信号产生时间上的二次相移.实现时间透镜最直接的方式是采用电光相位调制器(EOPM)[2]，正弦电压信号驱动电光晶体，可以使其对通过的光信号产生局部的二次时间相位调制.以EOPM为基础构建的时间成像系统不仅可以实现光脉冲压缩[3]，而且能有效抵御光通信系统传输线路上的色散畸变问题[4].但是用EOPM实现时间透镜存在两个方面的不足：只有在正弦调制峰值附近很小的范围内才能保证二次时间调制，而且最大相移量受限于最大耐受驱动电压，通常利用EOPM只能达到数π的相位调制.此外，利用非线性光学介质中的交叉相位调制(XPM)也可以实现时间透镜[5]，强泵浦光使介质的折射率发生变化，当弱信号光穿过介质时会获得二次时间相移.XPM类似于EOPM，要获得较大的相位调制，对泵浦光的功率要求很高，实现起来有一定困难和限制.相反，利用参量过程实现时间透镜，可以避免对功率要求过高的问题.四波混频(FWM)效应在高非线性光纤、硅波导，甚至任意光学材料之中，都能通过相位匹配来产生，而且FWM过程中输入输出波长非常接近，这样就为信号的发射和检测提供了很大的便利.近年来，利用FWM效应实现时间透镜成像系统，并已经广泛应用在光信号处理的各个方面[6-8].这里，在基于FWM原理的时间透镜成像系统中，通过数值计算分析了泵浦光脉冲宽度、泵浦光强度对放大因子M值的影响.其次，通过将成像系统中的光纤色散改进成指数渐减式，形成色散与非线性效应的动态完美匹配，能够使放大因子M值更趋近于理论值.

1光的时空二重性

沿z向传播并在横向方向发生衍射的傍轴空间光束、以及在色散介质中沿z向传输的窄带时间信号，它们各自的传输方程分别为

(1)

其中：Aspace为傍轴衍射光束的电场幅度；k为波矢量；Atime为窄带时间信号的电场幅度；τ为群延迟坐标系下的时间量；β2为色散介质的二阶色散参数，式(1)是光的时空对应原理的数学基础.

一个时间成像系统通常由输入色散元件(色散量φ″1)、时间透镜(二次相移Φ(τ))、输出色散元件(色散量φ″2)三部分组成.任意光脉冲进入时间成像系统后能够形成清晰像的条件为

(2)

式中φ″f为时间透镜的焦距色散，当满足上述成像条件时，放大倍数为M=-φ″2/φ″1.此时，输出光脉冲与输入光脉冲波形相似，区别仅在于振幅和脉宽不同.适当选择两个色散元器件的色散量，当M>0时，光脉冲正序排列，当M<0时，光脉冲反序排列；当|M|>1时光信号被拉伸，而|M|<1当时，光信号被压缩.

2时间透镜成像系统框图

如图1所示，时间透镜成像系统由输入光纤、时间透镜及输出光纤三部分组成.

图1　时间透镜成像系统Fig.1　The temporal imaging system based on time lenses

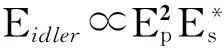
3时间透镜成像系统特性分析

在图1中,第一段光纤的参数为：β2i=-10ps2/nm/km,Li=1km，光信号经历的色散量为φ″1=β2iLi=-10ps2/nm；第二段色散光纤的参数为：β2i=160ps2/nm/km,Li=1km，光信号经历的色散量为φ″2=β2oLo=160ps2/nm.泵浦光经过的光纤参数为β2p=-10ps2/nm/km,Lp=2km，经历的色散φ″p=β2pLp=-20ps2/nm.波长选择为：λs=1.55μm,λp=1.547μm.以脉宽为1ps、间距为3.5ps的高斯光脉冲对输入时间透镜成像系统，通过FFT数值计算方法求解非线性薛定谔方程，可以了解光脉冲对的演变情况.在FWM效应形成的时间透镜中，φ″f=-φ″p/2=10ps2/nm，类比空间成像系统，当物距等于透镜焦距时，光脉冲经过透镜后波形会变换成频谱形状.如图2所示，信号光经过第一段光纤的色散变换到频域波形，相反在第二段光纤中，经过FWM所生成的闲置光则从频谱波形再次转变到时域波形，但光脉冲对在时间轴上被拉伸了16倍，而且前后光脉冲的顺序倒转了.

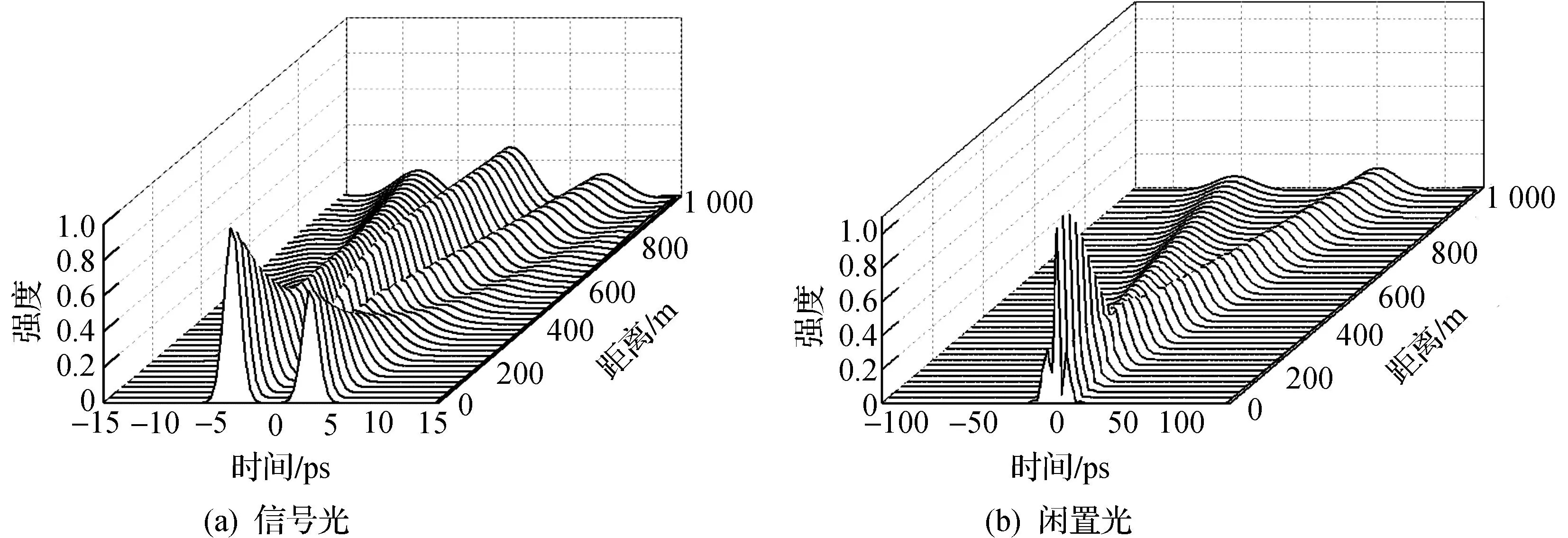
图2　信号光和闲置波在两段色散光纤中的波形演化Fig.2　The waveform evolution of a pair of pulses in two different fibers

图3　光脉冲对在时间透镜成像系统中的输入输出波形对比Fig.3　Waveform Comparison between input and output of imaging system

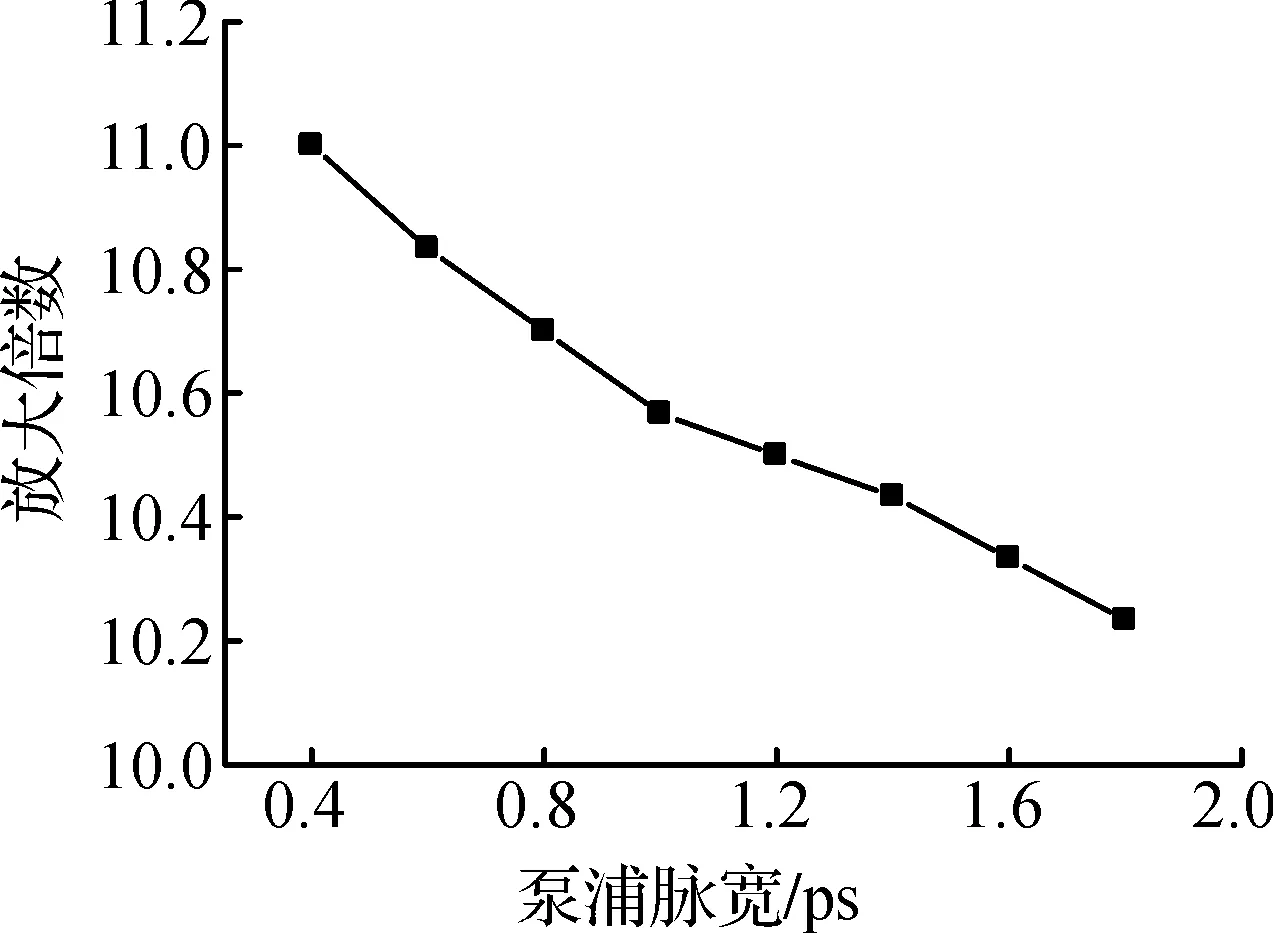
图4　泵浦光脉宽对放大倍数的影响Fig.4　Magnify factor under different width of pump pulse

图5　两种不同色散设计对放大倍数的影响Fig.5　Reduced aberration of M value using exponential dispersion parameter

图3显示了整个时间透镜成像系统的输入输出波形的脉宽变化.在信号光所有参数均保持不变的情况，如图4所示，我们使泵浦光的脉冲宽度从0.4 ps变化到1.8 ps，测量到成像系统的放大因子随泵浦光宽度的增大而有所下降.改变泵浦光功率，以及信号光功率，都对放大因子无任何影响.考虑到光信号在光纤中传输时受损耗作用，功率会随着传播距离而减少，为了更好地匹配色散与非线性效应，将色散由固定值改进成指数渐减，即β2(z)=β20e-αz，结果发现成像系统的放大倍数更加接近于理论值.如图5所示，当第二段光纤的色散从100 ps2/nm变化到400 ps2/nm，采用固定色散与指数渐减色散两种

情况下的观测结果，显然指数渐减式色散减少了与理论值的偏差，这主要是由于色散与非线性效应的完美匹配改进了成像系统的性能.

4结论

数值计算分析了基于四波混频效应的时间透镜成像规律，合理设计两段光纤的色散量，可以明显观测到光信号的放大作用.泵浦光的脉冲宽度对放大倍数有一定影响，泵浦光增宽，放大倍数减小，但泵浦光功率对放大倍数几乎没有影响.采取指数渐减的色散设计方式，使色散与光纤的非线性效应形成动态完美匹配，可以使实际系统的放大倍数更加趋近于理论结果，能够有效提高成像系统的性能.

参考文献：

[1]KOLNER B H, NAZARATHY M. Temporal imaging with time lens[J].Optics Letters,1989,14(12):630-632.

[2]李博，谭中伟，张晓兴.利用电光相位调制和交叉相位调制制作时间透镜的实验及仿真分析[J].物理学报，2011，60(8):257-264.

[3]常硕，娄淑琴，李博，等.增大基于电光相位调制的时间透镜孔径的参数调制法[J].光学学报，2014，34(9):73-78.

[4]何舟，梅君瑶，黄德修，等.一种基于时间透镜的10Gb/s无色散补偿光纤通信系统[J].中国激光，2011，38(1):144-149.

[5]李博，谭中伟，张晓兴.利用交叉相位调制和四波混频制作的时间透镜的信号分析[J].物理学报，2012，61(1):155-164.

[6]KEITH G P, MARK A F. Full 160-Gb/s OTDM to 16x10-Gb/s WDM conversion with a single nonlinear interaction [J]. Optics Express,2013,21(1):508-518.

[7]REZA S, MARK A F, AMY C T ,et al. Optical time lens based on four-wave mixing on a silicon chip[J]. Optics Letters,2008,33(10):1047-1049.

[8]MARK A F, REZA S, YOSHITOMO O, et al. Ultrafast waveform compression using a time-domain telescope [J]. Nature Photonics,2009,3(10):581-585.

(责任编辑：刘岩)

作者简介：郭淑琴(1970—)，女，山西夏县人，教授，研究方向为光通信技术，E-mail：guosq@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(60977020)

收稿日期：2014-12-21