桁架结构桥梁静气动系数试验研究

毛文浩 周志勇

(同济大学土木工程防灾国家重点实验室，桥梁结构抗风技术交通行业重点实验室，上海 200092)

桁架结构桥梁静气动系数试验研究

毛文浩 周志勇*

(同济大学土木工程防灾国家重点实验室，桥梁结构抗风技术交通行业重点实验室，上海 200092)

以岳阳洞庭湖二桥为工程背景，进行了节段模型风洞试验，测得桁架梁静力三分力系数和静力两分力系数；根据风洞试验结果分析了桁架主梁静气动系数变化规律，给出顺桥向风荷载的计算公式；将洞庭湖二桥、四渡河大桥以及北盘江特大桥的静力三分力试验结果与国内外规范进行对比分析，为桁架结构主梁气动系数选取提出建议，完善我国抗风规范中关于桁架桥梁静气动力方面的规定，使其更好地应用到设计中，为桁架桥静风荷载的确定提供参考。

桁架结构主梁, 顺桥向风荷载, 静气动系数, 规范

1 引 言

在大跨度桥梁设计中，风荷载往往是控制荷载。对于大跨度桥梁抗风性能的验算可分为静力和动力验算[1]。其中，静力验算是以设计风速为依据来计算作用于桥梁结构上的风荷载，按照静力学的检验方法来验算桥梁结构在该风荷载作用下结构的安全性，这就要求我们准确掌握风荷载计算方法及桥梁不同截面形式的气动参数。

桁架和箱形断面是大跨度桥梁常用的两种断面形式。随着大跨度桥梁的发展，桁架结构形式不断地被应用在大跨度桥梁中。由于桁架结构自身的特性，在风荷载作用下，桁架结构的静气动特性与普通的实腹式结构有所区别。特别是对于主桥顺桥向的风荷载的计算，我国《公路桥梁抗风设计规范》(JTG/T D60-01-2004)[2]中对于非桁架断面，通过考虑主梁上下表面之间的摩擦力来进行计算。对于桁架断面，除摩擦力外，还存在顺桥向的风阻力。在结构计算中，对于一般的实腹式截面，主梁上的风荷载可根据规范或风洞试验结果直接作用在截面形心位置，而对于桁架断面，风荷载应均匀施加到各杆件上，且其迎风面和背风面桁架的荷载存在一定的比例关系[3]，因此我国抗风规范[2]引入了遮挡系数。

对于在风荷载作用下的桁架桥梁静气动力系数的研究和工程计算大部分是建立在0°横向风作用下主梁的静气动力系数的基础上，然而实际的当地主导风向往往与桥跨的法向存在一定偏角，且由于斜风作用下很可能引起较0°横向风作用下更大的风荷载。因此，还应对桁架桥顺桥向阻力引起重视。

目前，对于桁架结构主梁的抗风性能研究较少，特别是对于顺桥向阻力的考虑缺乏系统的研究。戴伟[4, 5]基于上海闵浦大桥双层空腹钢桁架结构，通过对各风偏角的横向风作用下的主梁的静气动力系数的分解，初步探讨了桁架结构主梁在斜风作用下的静风力系数的计算方法。Zhu等[6]研究了斜风作用下青马大桥的六个静气动力系数。研究结果表明，气动阻力系数、气动升力系数和气动扭矩系数明显大于顺桥向阻力系数、气动摇摆力矩系数和气动偏转力矩系数。升力系数基本不随着风偏角变化，而阻力系数随着风偏角的增大而减小，气动扭矩系数随着风偏角的增大而增大。Swigert等[7]研究了Rifle桥桁架结构主梁的实际风荷载，并与3D模型的计算风荷载进行了对比。高亮[8, 9]利用风洞试验方法针对桁架梁断面和流线型断面两种典型的主梁截面形式进行了气动措施和附属设施对主梁三分力系数的影响分析。陈原[10]以安庆长江铁路大桥为背景，通过节段模型试验，总结了钢桁架主梁断面在宽度、高度、宽高比、主桁片数量、主桁片实度比以及边主桁片倾斜度发生变化时，静力三分力系数的变化趋势，为我国铁路桥梁规范风荷载计算的完善提供了一定的参考价值。

在各国规范中，我国《公路桥梁抗风设计规范》(JTG/T 060-01-2004)[2]仅给出静力三分力中阻力的计算以及跨径小于200 m的桁架桥梁顺风向荷载的计算公式(第4.3.6条)，忽略了升力和升力矩。在第4.3.5条仅给出的“断面形状复杂的主梁的空气静力系数宜结合风洞试验综合确定”的规定。《公路桥梁抗风设计指南》[11](以下简称《指南》)中给出了阻力、升力系数以便做参考计算，但没有用于桁架的三分力系数。各国规范，如英国BS5400规范[12]、美国AASHTO规范[13]等都较少涉及桁架构件的静气动力的计算条文，桁架桥梁顺桥向风荷载的规定则几乎没有。因此，考虑桁架桥在风荷载作用下的受力复杂性，对桁架桥梁进行静气动力参数的研究具有重要意义。

本文以洞庭湖二桥为工程背景，通过节段模型风洞试验研究了桁架主梁在不同风攻角和不同风偏角下的静气动力系数，并将洞庭湖二桥、四渡河大桥以及北盘江特大桥的静力三分力试验结果与国内外规范进行对比分析，为桁架结构主梁气动系数的选取提供参考。

2 工程概况

岳阳洞庭湖二桥位于洞庭湖长江入口处，东起岳阳，西接君山，是杭瑞高速公路临湘(湘鄂界)至岳阳公路的控制性工程，也是我国承东启西的重要公路运输通道。大桥上游距岳阳洞庭湖大桥3 km，下游距拟建的荆岳铁路洞庭湖大桥2 km。洞庭湖二桥桥跨布置为460 m+1480 m+491 m的单主跨双塔悬索桥，桥型总体布置图见图1。加劲梁采用板桁结合梁，桁高9 m，矢跨比1∶10，钢桁梁标准断面图见图2。钢桁架梁节段标准宽度为36.1 m，索塔总高227.5 m，两根主缆横向间距为36.1 m。

3 桁架结构桥梁静气动力系数风洞试验研究

3.1 桥梁静气动力系数定义

静力三分力系数是指表征各类结构断面在平均风作用下受力大小的无量纲系数，它反映了风对桥梁的定常气动作用， 是确定结构静风荷载和其他动力响应的关键参数[14]。风对主梁的作用可以分解为三种力，按桥梁断面本身的体轴坐标系和风轴坐标系来分别定义，即体轴坐标系下的三分力分别记为阻力、升力和扭矩，风轴坐标系下的三分力分别记为阻力、升力和扭矩，如图3所示。

图1 洞庭湖二桥桥型总体布置图(单位：cm)

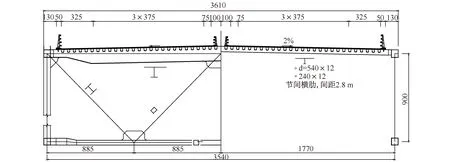
图2 洞庭湖二桥钢桁梁标准断面图(单位：cm)

图3 横风向静力三分力示意图

风轴上的阻力系数、升力系数以及升力矩系数定义如下：

(1)

主梁体轴上的阻力系数、升力系数以及升力矩系数定义如下：

(2)

主梁体轴系三分力与风轴系三分力之间的转换如下列式子所示：

FD=FHcosα+FVsinα

(3)

FL=-FHsinα+FVcosα

(4)

式(1)—式(4)中，FD，FL和MT分别表示风轴系上静风阻力、静风升力和静风升力矩；FH，FV和MT分别表示体轴系上静风阻力、静风升力和静风升力矩；ρ表示空气质量密度，取ρ=1.225 kg/m3；U表示来流风速；H，B及L分别表示节段模型投影高度、投影宽度及投影长度；θ表示来流攻角。

不同风偏角下，静力两分力方向定义如图4所示。

图4 斜风作用下静力两分力方向示意图Fig.4 Static two-component coefficients under skew winds

静力两分力风轴上的横桥向阻力系数、顺桥向阻力系数定义如下：

(5)

主梁体轴上的横桥向阻力系数、顺桥向阻力系数定义如下：

(6)

主梁体轴系两分力与风轴系两分力之间的转换如下列式子所示：

Fd1=Fh1cosθ+Fh2sinθ

(7)

Fd2=-Fh1sinθ+Fh2cosθ

(8)

式(5)-式(8)中，Fd1,Fd2分别表示风轴系上横桥向阻力与顺桥向阻力；Fh1,Fh2分别表示体轴系上横桥向阻力与顺桥向阻力；ρ表示空气质量密度，取ρ=1.225 kg/m3；U表示来流风速；H,B及L分别表示节段模型投影高度、投影宽度及投影长度；θ表示来流偏角。

桥梁静气动力系数的识别，工程主要是通过节段模型风洞试验和数值模拟的方法进行。但是对于桁架结构，由于空间结构的复杂性，还没有比较有效的方法进行桁架结构的CFD数值模拟，因此，对桁架结构静气动力系数的研究基本上还是采用风洞试验的方法进行。

3.2 钢桁梁主梁断面静力三分力试验

钢桁梁主梁断面静力三分力试验研究采用几何缩尺比1:70刚体节段模型(图5)，针对洞庭湖二桥成桥状态和施工状态主梁节段进行三分力系数试验研究，试验在同济大学TJ-2风洞中进行。模型长度L=1.72 m，高度H=0.129 m，宽度B=0.516 m，整个模型长宽比约为3.3。主梁测力节段模型是在测振节段模型基础上加以改造，竖直安装在底支式五分量测力天平上。试验在均匀流场中进行，试验风速固定为10 m/s，共完成了-12°～12°,共计25个风攻角。试验结果包括在不同风攻角下，成桥状态和施工状态主梁的静风阻力和阻力系数、静风升力和升力系数以及静风升力矩和升力矩系数。

图5 洞庭湖二桥刚体模型静力三分力试验模型

3.3 钢桁梁主梁断面静力两分力试验

钢桁梁主梁断面静力两分力试验研究采用几何缩尺比1∶70刚体节段模型(图6)，针对洞庭湖二桥成桥状态和施工状态主梁节段进行两分力系数试验研究，试验在同济大学TJ-2风洞中进行。模型总长度L=1.72 m，高度H= 0.129 m，宽度B=0.516 m，整个模型长宽比约为3.3。为了减少由于模型端部三维绕流效应对测试段静力两分力的影响，提高测试的精度，将主梁截为三段，其中两端为补偿段，长度为0.31 m，中间测试段长度为1.10 m。补偿段的外形与测试段完全相同，且固定在测试段两端，不与测试系统接触。主梁测试段水平安装在底支式六分量测力天平上。试验在均匀流场中进行。试验风速固定为10 m/s，考虑模型对称性，共完成了0°～90°，共计10个风偏角。试验结果包括在不同风偏角下，成桥状态和施工状态主梁的横桥向阻力和阻力系数以及顺桥向阻力和阻力系数。

图6 洞庭湖二桥刚体模型静力两分力试验模型

3.4 试验结果

图7、图8分别给出了洞庭湖二桥成桥状态和施工状态的静力三分力系数和静力两分力系数的试验结果。

图7 静力三分力系数

图8 静力两分力系数

4 试验结果分析

通过对桁架结构主梁的风洞试验，可以得到以下结论：

(1) 从图7可以看出，在小攻角范围内，CH和CM均为正值，说明该桁架断面具备气动稳定的必要条件。

(2) 对于阻力系数CH，在所关心的小攻角(-3°～+3°)范围内，阻力系数的值与0°攻角的数值相近。但从图8结果可以看出，在小偏角情况下，CH最大值略大于0°偏角的值，这是由于斜风作用下，横风向受力面较0°风偏角时大；随着风偏角的逐渐增大，CH逐渐减小。

(3) 桁架断面顺桥向阻力系数随着风偏角的增加，呈先增大后减小的趋势，该断面在风偏角为50°时出现极大值，这是由于桁架断面在大偏角情况下，顺桥向迎风面积达到最大。

(4) 从成桥状态和施工状态的结果对比可以看出：①由于栏杆等桥面附属设施的存在，阻力系数增大；②升力系数和升力矩系数减小，且升力系数的不规律性增大。

(5)《公路桥梁抗风设计规范》[2]规定，跨径小于200 m桁架桥梁的顺桥向风荷载为横桥向风荷载的0.50倍，然而对跨径超过200 m的桁架桥梁顺桥向风荷载并没有给出参考值。从图8可以看出，顺桥向的风荷载与横桥向单位长度风荷载之间并不是简单地呈一定的比例关系。

由式(6)可知，在顺桥向阻力系数和横桥向阻力系数定义中，特征长度的取值不相同，因此，为了统一，图9给出了成桥和施工状态单位长度顺桥向风荷载与单位长度横桥向风荷载比值随偏角的变化规律(70°～90°偏角时，比值较大，影响曲线的直观性，这里没有给出)。

由图9可见，在45°偏角范围内，单位长度顺桥向阻力与单位长度横桥向阻力的比值随偏角变化可以偏安全地认为成线性关系。由于施工周期较短，且施工阶段的阻力值较小，在此，仅对成桥状态两者的比值进行线性拟合。以阻力比值为y轴，以风偏角(角度)为x轴，拟合得曲线为y=0.0213x+0.0333(图9中拟合曲线)。由图9可以看出，在45°偏角情况下，阻力比值接近1，这也进一步说明了拟合结果的正确性。

图9 顺桥向阻力/横桥向阻力-风偏角曲线Fig.9 Longitudinal drag forces/lateral drag forces vs. wind yaw angle curve

在大偏角的情况，由于桁架断面构造复杂，阻力的比值出现明显的非线性，应进行风洞试验进一步确定桁架结构顺桥向阻力值。

5 试验结果与各国规范的比较

规范中的具体条文是指导工程建设最重要的指标，其给出的计算方法等是建立在大量的工程实践和经验的基础上，具有科学意义，并且具有普遍适用性。但随着桥梁的发展，规范中的部分条文已经不能满足设计要求。特别是对于桁架桥梁，我国《公路桥梁抗风设计规范》[2]仅给出静力三分力中阻力的计算，忽略了升力和升力矩，也没有给出跨径大于200 m的桁架桥梁顺风向荷载的计算公式。《指南》[11]中仅给出了阻力、升力系数以便作参考计算，但没有用于桁架的三分力系数。各国规范，都较少涉及桁架构件的静气动力的计算条文。

为了使对比结果更具有普遍性，本文在此给出宜恩公路四渡河大桥和贵州省北盘江特大桥的断面示意图(图10、图11)以及三分力系数试验结果(图12)。四渡河大桥和北盘江特大桥节段模型测力试验均在同济大学TJ-1号风洞进行。

图10 宜恩公路四渡河大桥钢桁梁标准断面图(单位：cm)

图11 北盘江特大桥钢桁梁标准断面图(单位:cm)

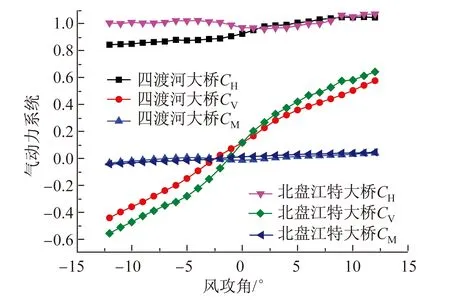
图12 成桥状态静力三分力系数

5.1 公路桥梁抗风规范、设计指南与英国BS5400规范

5.1.1 阻力系数

我国《公路桥梁抗风设计规范》[2]中，关于桁架桥风载阻力系数的规定是借鉴英国BS5400规范[2]中的相关条文，仅仅是在表达方式上有一些差异，但本质上是相同的。

我国《公路桥涵设计通用规范》(JTG D60-2004)[15]和《公路桥梁抗风设计规范》(JTG/TD60-01-2004)[2]中风荷载的计算表达式虽略有不同，但对《公路桥涵设计通用规范》中的表达式进行合理的变换后[10]，两者的计算表达式便可保持一致。

在计算时取一个节间长度，根据《公路桥梁抗风设计规范》(JTG/T D60-01-2004)[2]第4.3.4条，计算可得三座桥梁桁架断面实面积比和间距比。由此可得桁架构件的风载阻力系数以及桁架遮挡系数。桥面系构造的风载阻力系数取1.3。在抗风规范中给出的阻力系数是针对桁架构件的，因此将桥面系、迎风桁架和非迎风桁架的阻力求和就可以得到桁架结构的总阻力的规范值。总阻力的试验值采用0°攻角的阻力值。三个桁架断面阻力值比较见表1。

由结果对比可知，规范阻力值高出试验值较多。因此，根据公路桥梁抗风规范计算所得到的风载阻力是偏于安全的。

5.1.2 升力系数

对于升力系数的研究，抗风规范并没有给出升力系数的规定，可以参考《指南》[11]中的相关规定。根据《指南》[11]第4.3.2.5条，当攻角小于1°时，主梁竖向气动力系数可按照《指南》[11]图4.3.2.5选取；当攻角为1°～5°之间时，主梁竖向气动力系数取0°攻角的0.75倍。

表1 风载阻力规范值与阻力试验值(实桥风速为U)

Table 1 Code values and test values of drag forces (Under the actual wind speed U)

在此，选取0°和+3°攻角下桁架主梁的升力系数试验值与规范值比较，结果见表2。

表2 风载升力系数规范值与升力系数试验值

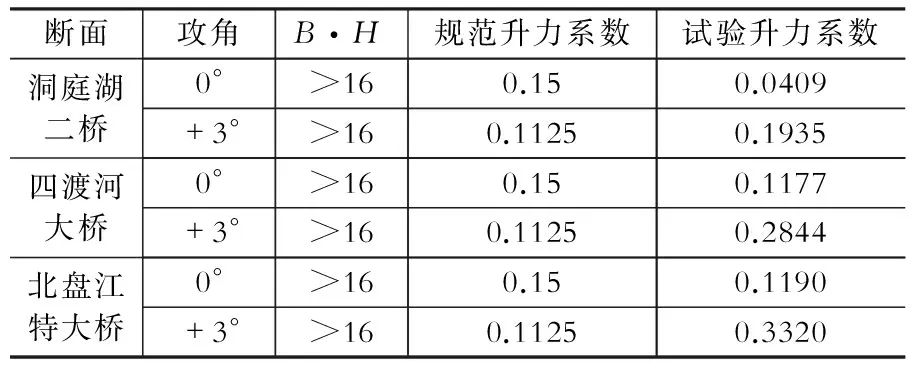
Table 2 Code coefficient and test coefficient of lift force

从表2可以看出，在0°攻角情况下，《指南》[11]提供的升力参考值均大于试验值，且对于四渡河大桥和北盘江特大桥，规范值和试验值吻合较好，结果偏安全。而在+3°时，升力规范值大大低于试验值。从而可知，《指南》[11]给出的升力值并不具有普遍性，仅可作为参考。另外，由于该条文给定的参考值仅仅与主梁侧向的投影宽度和高度乘积有关，忽略了主梁的构造等其他因素的影响，考虑因素太少。当攻角为1°～5°之间时，主梁竖向气动力系数取0°攻角的0.75倍，这显然也不满足升力系数是随着攻角的增大而增大的规律。因此，此条文的适用条件还有待进一步的研究。

由于桁架断面构造的复杂性，在进行静风荷载计算时，其升力系数可根据风洞试验结果偏安全地选取-3°～+3°范围内的最大值。

5.2 美国AASHTO规范[13]

5.2.1 阻力系数

AASHTO规范假定风荷载均匀分布在结构表面上，风荷载作用的面积为所有构件、桥面系等附属设施在垂直于来流方向上的投影面积之和。结构的阻力大小由风压与作用面积之和。规范中对于桁架结构，要求迎风弦杆平面内风荷载部的小于4.4 N/mm，背风弦杆平面内风荷载部的小于2.2 N/mm。但由于试验风速一般较小，此项要求很难满足，因此在以下讨论中忽略此条要求。

规范中给出基本风速VB=160 km/h桁架的风压值，上风向为0.002 4 MPa，下风向为0.001 2 MPa。根据规范要求，可得到相应于试验风速10 m/s下的换算风压：

(9)

式中，PD表示换算后的风压，试验风速VDZ=10 m/s=36 km/h。

因此，由式(9)可得PD上=121.5 Pa，PD下=60.75 Pa。

取一个节间长度，根据AASHTO规范[13]，计算三座桥梁成桥状态的阻力规范值。阻力试验值根据0°攻角下的阻力系数进行计算，实桥风速取10 m/s。结果对比见表3。

表3 AASHTO规范阻力值与阻力试验值

Table 3 AASHTO value and test value of drag force

由表1和表3的对比结果可知，AASHTO规范[13]与我国《公路桥梁抗风设计规范》[2]所计算的阻力值较为接近，但是均远大于试验值，规范值偏于安全。

6 关于规范中桁架桥梁静气动参数计算的讨论和建议

为了方便讨论，将风载阻力对比结果列表见表4，升力系数结果见表2。

从以上对各国规范的比较分析可以看出，我国规范中对于桁架桥梁静气动力的计算方面还存在一些不足，仍需要进一步的完善。

表4 各国规范阻力规范值与试验值比较结果

Table 4 Comparison of various code value and test value of drag force

关于横桥向阻力系数，我国规范中给出的桁架构件阻力系数虽然偏于保守，但其考虑的因素仍然不足：①倾斜桁架与非倾斜的桁架的阻力系数显然存在差异，可以参考《公路桥梁抗风设计规范》[2]第4.3.3条，对阻力系数根据倾斜角进行折减；②对遮挡系数而言，当上部结构为两片或者两片以上桁架时，非迎风桁架的阻力系数在《公路桥梁抗风设计规范》[2]中采取相同的值，这显然过于保守。可以根据间距比对第三片及第三片以上的桁架的阻力系数进行进一步折减；③可以参考美国AASHTO规范[13]的方式，采用风压与面积的乘积来确定阻力值。

对于顺桥向阻力系数，我国规范参考英国BS5400规范[12]，对跨径小于200 m的桁架桥梁建议取横桥向阻力的0.5倍。然而，在研究中发现，对于大跨度桥梁，单位长度顺桥向荷载与单位长度横桥向荷载的比值不仅仅是存在单一的比例关系，可以采用线性曲线进行拟合，拟合的结果为y=0.0213x+0.0333(阻力比值为y轴，以风偏角(角度)为x轴)。

关于升力系数，虽然我国规范中有涉及，但不是针对桁架断面提出。虽然在《指南》[11]中给出了升力系数的参考值，但是由于该条文给定的参考值仅仅与主梁侧向的投影宽度和高度乘积有关，忽略了主梁的构造等其他因素的影响，考虑因素太少，参考值与试验值差别也较大，甚至比试验结果偏小，从而可能产生安全隐患。

7 结 论

通过以上研究，可以得到以下结论：

(1) 从静力三分力系数曲线可以看出，在小攻角范围内，CH和CM均为正值，说明桁架断面具备气动稳定的必要条件。

(2) 对于阻力系数CH，在所关心的小攻角(-3°～+3°)范围内，阻力系数的值与0°攻角的数值相近。CH最大值出现在小偏角情况下，这是由于斜风作用下，横风向受力面较0°风偏角时大。随着风偏角的逐渐增大，CH逐渐减小。

(3) 桁架断面顺桥向阻力系数随着风偏角的增加，呈先增大后减小的趋势，该断面在风偏角为50°时出现极大值，这是由于桁架断面在大偏角情况下，顺桥向迎风面积达到最大。

(4) 从成桥状态和施工状态的结果对比可以看出：①由于栏杆等桥面附属设施的存在，阻力系数增大；②升力系数和升力矩系数减小，且升力系数的不规律性增大。

(5) 对于桁架结构主梁的阻力系数，可参考美国AASHTO规范[13]的方式，采用风压与面积的乘积来确定阻力值。

(6) 对于桁架结构主梁顺桥向阻力单位长度顺桥向荷载与单位长度横桥向荷载的比值，可以采用线性曲线进行拟合，拟合的结果为y=0.0213x+0.0333(以风偏角(角度)为x轴，阻力比值为y轴)。

(7) 桁架桥梁升力系数应该考虑高度、宽度和风攻角的影响，并进一步考虑桁架构件的特性后进行确定。升力系数的取值仍有待进一步的研究。

[ 1 ] Davenport A G. The application of statistical concepts to the wind loading of structures[C]. ICE Proceedings: Thomas Telford, 1961, 19(4): 449-472.

[ 2 ] 中华人民共和国交通部. JTG/T D60—01—2004公路桥梁抗风设计规范[S].北京:人民交通出版社,2004.

Ministry of Communications of the People’s Republic of China. JTG/T D60—01—2004 Wind-resistent design specification for highway bridges[S]. Beijing: China Communications Press, 2004.(in Chinese).

[ 3 ] ECCS. Recommendations for calculating the effects of wind on Constructions [M]. 2nd Edition. ECCS Technical Committee 12, Brussels, Belgium, 1987.

[ 4 ] 戴伟.桥梁桁架构件气动力参数研究[D].上海:同济大学,2007.

Dai Wei. Study on the aerodynamic parameters of truss members of bridges[D]. Shanghai: Tongji University, 2007.(in Chinese)

[ 5 ] 戴伟,马如进.上海闵浦大桥桁架结构主梁斜风下的气动力参数研究[J].上海公路, 2009, 1: 26-30.

Dai Wei, Ma Rujin. Study on the aerodynamiz parameters of truss girder of Shanghai Minpu Bridge under skew wind[J]. Shanghai Highways, 2009, 1:126-30.(in Chinese)

[ 6 ] Zhu L D, Xu Y L, Zhang F, et al. Tsing Ma bridge deck under skew winds—part I: aerodynamic coefficients[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(7): 781-805.

[ 7 ] Swigert W B, Rutz F R, Reus K L. Wind load analysis of a truss bridge at rifle Colorado[D]. Forensic Engineering: Proceedings of the Congress: American Society of Civil Engineers, 2006: 256-270.

[ 8 ] 高亮.桥梁断面三分力系数试验研究[D].西安:长安大学,2010.

Gao Liang. Investigation into three-component force coefficients of bridge deck Section[D]. Xi’an: Chang’an University, 2010.(in Chinese)

[ 9 ] 高亮,刘健新,张丹.桁架桥主梁三分力系数试验[J].长安大学学报(自然科学版),2012:32(1):52-56.

Gao Liang, Liu Jianxin, Zhang Dan. Experimental study on three-component force coefficients of truss girder cross-section[J]. Journal of Chang’an University(Natural Science Edition), 2012: 32(1): 52-56.(in Chinese)

[10] 陈原.大跨度铁路桥梁钢桁架主梁气动参数研究[D].成都:西南交通大学,2012.

Chen Yuan. The study of aerodynamic parameter for steel truss girder of long span railway bridge[D]. Chengdu: Southwest Jiaotong University, 2012.(in Chinese)

[11] 公路桥梁抗风设计指南[M]. 北京：人民交通出版社, 1996.

[12] British Standard 5400. Steel, concrete and composite bridges[S]. British Standard Institution, London, 1986.

[13] AASHTO-LRFD. Bridge design specifications(SI Units Third Edition)[S]. American Association of State Highway and Transportation Officials, Washington, D.C., 2004.

[14] Simiu E, Scanlan R H. Wind effects on structures: an introduction to wind engineering[M]. New York: John Wiley and Sons, 1978.

[15] 中交公路规划设计院.JTG D60—2004公路桥涵设计通用规范[S].北京：人民交通出版社，2004.

CCCC Highway Consultants Co., Ltd. JTG D60-2004 General code for design of highway bridges and culverts[S]. Beijing: China Communications Press, 2004.(in Chinese)

Study on the Static Aerodynamic Coefficients of Truss Girder Bridges

MAO Wenhao ZHOU Zhiyong*

(State Key Lab for Disaster Reduction in Civil Engineering, Key Laboratory of Ministry of Communications for Bridge Structure Wind resistance , Tongji University, Shanghai 200092, China)

A steel truss section model wind tunnel test of the 2nd Dongtinghu Bridge was carried out to obtain the static three-component coefficients and two-component coefficients. The change rules of the static aerodynamic coefficients of the steel truss girder were investigated based on the test results and a formula of the longitudinal wind load was provided. Based on the comparison of the test results of the 2nd Dongtinghu Bridge, Sidu River Bridge and Beipan River Bridge and domestic and overseas codes and standards, some suggestions for determining the static aerodynamic coefficients of truss girder bridges were given, thus perfecting the provisions of truss girder bridge static aerodynamic coefficients in the domestic wind-resistant standards and serving as a reference for the static aerodynamic wind loads on truss girder bridges.

steel truss girder, longitudinal wind loads, static aerodynamic coefficients, codes and standards

2014-02-25

*联系作者，E-mail: z.zhou@tongji.edu.cn