基于应用型人才培养模式下的贝叶斯公式教学

刘国祥，杨永霞，张晓丽，刘　冬，由向平，李玉毛（赤峰学院　数学与统计学院，内蒙古　赤峰　024000）



基于应用型人才培养模式下的贝叶斯公式教学

刘国祥，杨永霞，张晓丽，刘冬，由向平，李玉毛
（赤峰学院数学与统计学院，内蒙古赤峰024000）

摘要：贝叶斯公式是《概率论与数理统计》中的一个重要公式，同时也是教学中的一个难点.根据笔者的教学经验，谈了对这一教学内容的教学设计和一些体会，探讨改革教学模式，渗透数学文化等措施.

关键词：概率论与数理统计；贝叶斯公式；教学设计；人才培养；应用能力

基于应用型人才培养模式的教学改革，文[1]讨论了《概率论与数理统计》课程改革探索与实践，文[2]讨论了课程教学方法的改革.现在针对“贝叶斯公式”一堂课，讨论课堂教学.

贝叶斯公式是《概率论与数理统计》课程中的最重要公式之一，也是在现实生活中应用非常广泛的公式.它既涉及到全概率公式，又涉及到条件概率，是概率论课程教学中的一个重点，同时也是教学的一个难点.教学中常常出现以下问题：一是公式复杂，难于理解与记忆；二是应用困难，易与全概率公式混淆；三是对公式的作用认识模糊，不利于解决实际问题.针对上述弊端，基于应用型人才培养模式，我们对于贝叶斯公式的讲解给出新的尝试，并在教学中取得了良好的效果.

1　关于课题的引入

中小学数学教学，几乎每一节课，都需要有导言或者引例，有的学校定有制度，也几乎被人接受.至于高等学校数学教学，是否需要导言、引例等，不同的人有不同的认识.有人喜欢用，有人几乎不用.我们认为，要根据课程的特点，适当地选用简单明了的引例.宁缺毋滥，以防冲淡主要教学内容.当然，简单通俗的导言，应该尽量有，但是要精心设计.总结多年的教学，对于“贝叶斯公式”的教学，有效果比较好的两种方式.

1.1复习三个重要公式，启发导出贝叶斯公式

学生在前面的课堂学习中，已经对条件概率、乘法公式和全概率公式有了一定的了解和认识，本次课前先对这三个公式进行复习，板书，以备后用.

我们知道，全概率公式，简单的说是“已知原因求结果”.那么，在实际当中会不会遇到“已知结果求原因”的情况呢？启发引导学生思考该如何表述，如何解决.

也就是，“事件B发生了”——结果，那么它是由于“事件Ai发生导致的的概率有多大”——究其原因.那么，用严谨的数学式子表示就是：P(Ai|B),如何计算呢？这是条件概率，其中分子P(AiB)用到乘法公式，分母P(B)中用到全概率.写出来就是：

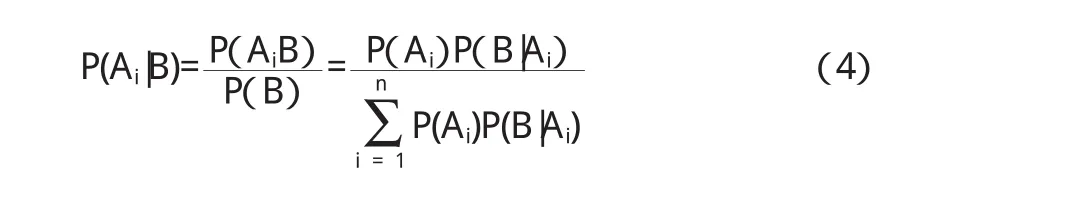
这就是贝叶斯公式，也叫逆概率公式.推导过程，就是基本的证明.简单明了，重点突出.

1.2通过简单易懂的实例，引入贝叶斯公式

引例一定要简单明了，最好来自于生活，学生易懂.切忌叙述过于复杂，有图有表有视频，分散了学生的注意力.

引例某学院新生有三班级，其中一班男生20人，女生30人；二班男生30人，女生20人；三班男生25人，女生25人.任意选择一个班级，再从中任意选一名学生做学生会主席，结果他是男生，问他是一班的概率是多少.

学生对这个背景非常熟悉，不需要常识介绍，马上就可以转入对问题的思考.

分析用Ai表示事件“学生会主席是i班的”，其中i=1, 2,3.

用Bi表示事件“学生会主席是男生”.

事件A1,A2,A3是完备事件组，相互独立.

问题“任意选择一个班级，再从中任意选一名学生做学生会主席，结果他是男生，他是一班的概率”，就是求概率P(A1|B).根据条件概率、乘法公式和全概率公式，计算：

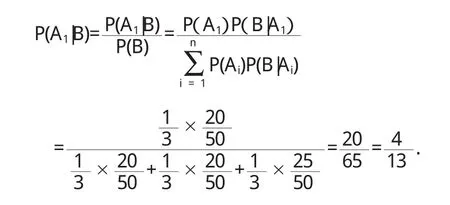
比较两种引入方法，我们更欣赏第一种.认真看看，第二种只是在第一种的基础上加了一个实际背景，计算、推导都一样，反而增加了对两个条件概率P(Ai|B)和P(B|Ai)理解.我们强调重视应用意识培养，但是比一定必须要“实际——理论——应用”的统一模式.向第一种那样“旧理论——新理论——（新）应用”也未尝不可.

2　贝叶斯公式及其证明

有了前面的导入，下面很容易写出完整的贝叶斯公式.这里要注意，公式一定要完整严谨，前边引出公式不完整、不严谨的地方，一定要详细说明，例如：A1,A2,A3,…,An是完备事件组（样本空间的一个划分）.

定理（贝叶斯公式）如果试验E的样本空间为S，事件A1,A2,A3,…,An是完备事件组，B是E的事件，并且P(B)>0,P (Ai)>0,(i=1,2,3,…,n)，则有

这一节课最简单的一点就是贝叶斯公式的证明，根据条件概率、乘法公式和全概率公式，可以直接写出.其实（4）就是比较完整的证明.

难点在于公式中对两个条件概率P(Ai|B)和P(B|Ai)=理解在“谁”的条件下，求“谁”的概率？在这里事件B“是结果”，它发生了，它是由于Ai发生“造成的”.根据全概率公式，B的发生由各个Ai发生都可能“造成”.每一个Ai发生而“造成”的可能性多大？这就是P(Ai|B).

3　通过典型例题，加深理解，强调应用

在现实生活中，贝叶斯公式有非常广泛的应用，如在疾病诊断、质量控制、安全监控等方面都发挥了重要的作用.在教学实践中，我们怎样科学合理地设置应用案例，将知识性与趣味性相互结合，能够培养学生思维的深刻性.

第一个例题应该比较简单，可以说是公式的直接套用，让学生学会使用这个公式.如果引例不是前边的例子，这里可以作为例题1.否则可以选用一般教材上的“三个工厂生产同一种产品，合格率”问题，第一问应用全概率公式，第二问应用贝叶斯公式.难度不大，容易理解.

第二例可以以不容易理解，甚至可能造成理解错误疾病诊断为例.这个例题在多本教材上出现，但是讲解都不深刻.武汉大学教材用了很长篇幅，但是没有说到重点上.

例题根据以往的临床记录，某一地区患有某种癌症的发病率为0.005.患者对一种试验反应是阳性的概率为0.95，正常人对这种试验反应是阳性的概率为0.02.现抽查了一个人，试验反应是阳性，问此人是此病患者的概率有多大？

题目难度不大，设A={抽查者患有癌症}，B={抽查者实验反应呈阳性}.那么={抽查者不患有癌症}.

对于这个结果怎样理解？P(B|A)=0.95说明95%的患者都能够检查出来（漏诊未查出来只有5%）；P(B)=0.02说明只有2%的误诊（或者说没有病，认为有病）.这表明检查水平比较高，但是，P(A|B)=0.1927，也就是，其正确性不足20%？

如果将这个实验用于普查，就是化验呈阳性的人真正患有这种癌症的不足20%.“其正确性不足11%”[5]的结论是不对的.教学中，对这个结果引导学生进一步分析，“某一地区患有某种癌症的发病率为0.005”，就是说这里平均1000人中有5人患这种病.而“P(A|B)=0.1927”说的是，检查呈阳性的人群中，10000人中大约有1927人患有这种癌症.二者比较0.1927÷0.005=38.54.这说明的是，“检查呈阳性的人群患有这种癌症”是“普通人群患有这种癌症”的38.54 倍.借用“非典”的说法，“疑似”人群是普通人群的21.32倍.这种检查是有意义的.

再进一步思考，检查呈阳性了，“疑似”了，怎么办？复查呗.对“疑似”人群进行复查.注意，这时候P(A)=0.1927，那么P()=1- 0.1927=0.8078.P(B|A)=0.95,

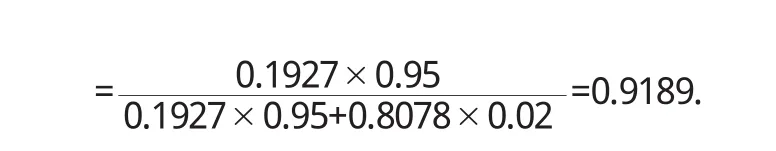
这就是说，对于“疑似”的人，复查检查仍然呈阳性，那么，他患有这种癌症的概率就从19.27%提高到91.89%，是“疑似”的0.9189÷0.1927=4.77倍，是普通人群的0.9189÷ 0.005=183.78倍，基本可以“确诊”.

当然，在医疗过程中医师根据经验，只有怀疑有这种癌症的人才做这种检查，也就是先筛查，发病率也远远不是0.005.

4　融入数学建模思想，培养应用意识

高等教育教学中，不但让学生学会数学，最重要的是要会用数学，用数学来分析问题、解决问题，也就是应用相应的数学理论知识去建立数学模型的能力.将数学建模思想方法融入数学类主干课程中已经成为教师的共识，但是什么时候融入，什么课程适合融入，怎么样融入，是我们一直在探索的课题.我们认为，贝叶斯公式就是非常适合的一个内容.

案例1：“拼写纠正”问题：在文字输入时，我们发现当用户输入了一个在字典中不存在的单词时，我们就需要去猜测，他到底真正想输入的单词是什么呢？用概率论中我们形式化的语言来叙述就是，我们需要求：P(他真正想输入的单词|他实际输入的单词)这个概率，并且找出那几个使得这个概率最大的猜测单词，甚至于对他们排序.比如用户输入：thew，那么他到底是想输入the，还是想输入thaw？到底哪个猜测可能性更大呢？

案例2：“通讯信号估计”问题：通讯系统由信源、信道、编码、译码和干扰源等几部分组成.信源发出来的消息是随机的，而由于信道中存在干扰，进入信道的某个信号，从信道出来的信号可能就不再是这个信号了.我们的问题是，当接收到一个信号后，进入信道的信号到底是什么？

案例3：“股票行情分析”问题：为了分析预测一支股票未来一定时期内的价格变化,我们可以分析影响股票价格的因素,比如利率的变化.若该支股票上涨了,试分析确实是由于利率下调引起股票上涨的概率.

5　简单介绍数学家，了解数学史，渗透数学文化

在课堂上适当介绍数学史与数学家，特别是概率论与数理统计学学家，渗透数学文化[2].一是能够减少课堂枯燥，二是提高学生兴趣，三是使学生初步了解科学发展的基本脉络.

托马斯•贝叶斯(Thomas Bayes,1701—1761)英国牧师，业余数学家.他生前是位受人尊敬英格兰长老会牧师.为了证明上帝的存在，发明了概率统计学原理，非常令人遗憾的是，他的这一愿望至死也未能实现，当然，也不可能实现.贝叶斯在数学方面主要研究概率论，他将归纳推理法用于概率论基础理论，创立了贝叶斯统计理论，对于统计推断、统计决策函数、统计估算等做出了重要贡献.1763年发表了这方面的论著，对于现代概率论和数理统计都有很重要的作用.贝叶斯的另一著作是发表于1758年的《机会的学说概论》.

贝叶斯所采用的许多术语被沿用至今.贝叶斯思想和方法对概率统计的发展产生了深远的影响.现在，贝叶斯思想和方法在许多领域都获得了广泛的应用，

6　结语

任何人，当然包括学生，要善于总结，进行反思.古人讲日三省其身，“省”什么，其中重要方面就是总结与反思.即使不能对事物进行事前准确预测，但是事后必须总结反思，做个“事后诸葛亮”.如果“失了街亭”，要反思其原因，这是因为什么.“一来是马谡无谋少才能，二来是将帅不和”“才失了街亭”.再跟深入地问一句，因素“马谡无谋少才能”和“将帅不和”各自占多大的比例.哪一个是决定性的.这就用到贝叶斯方法.

参考文献：

〔1〕刘国祥，等.应用型人才培养模式下概率论与数理统计课程改革探索与实践[J].赤峰学院学报，2014（11）.

〔2〕张晓丽，刘国祥，等.应用型人才培养模式下《概率论与数理统计》课程教学方法的改革与探讨[J].赤峰学院学报，2015（4）.

〔3〕程小红.贝叶斯公式的几个应用[J].大学数学，2011，27(2).

〔4〕魏宗舒.概率论与数理统计教程[M].北京:高等教育出版社，2004.

〔5〕盛骤，谢式千，潘承毅.概率论与数理统计教程（第四版）[M].北京:高等教育出版社，2008.6.

〔4〕李大潜.将数学建模思想融入数学类主干课程[J].工程数学学报，2005(8):2-7.

〔6〕叶其孝.微积分教学中融入数学建模的思想和方法[J].数学通报，2014(3):40-47.

〔7〕百度百科.http://baike.baidu.com/view/77778.htm?fr=a1-addin，2014.09.28.

基金项目：赤峰学院教学改革研究项目（JGXM201427）

中图分类号：G642

文献标识码：A

文章编号：1673- 260X（2015）01- 0227- 03