低渗透致密气藏水平井探测半径研究

陈志明，廖新维，赵晓亮，窦祥骥，祝浪涛

(教育部石油工程重点实验室中国石油大学，北京 102249)

低渗透致密气藏水平井探测半径研究

陈志明，廖新维，赵晓亮，窦祥骥，祝浪涛

(教育部石油工程重点实验室中国石油大学，北京 102249)

为解决低渗致密气藏水平井的探测半径计算问题，建立了考虑渗透率动态效应和应力敏感下水平井渗流模型，并以鄂尔多斯盆地致密气藏为例，采用数值离散法得出水平井探测半径。结果表明:鄂尔多斯盆地致密气藏水平井探测半径曲线的拟合系数为1.2～1.3，小于未考虑渗透率动态效应和应力敏感的情形;水平井探测半径由小至大依次为考虑动态渗透率和压力敏感效应的情形，只考虑动态渗透率效应的情形，只考虑压力敏感效应的情形和不考虑动态渗透率和压力敏感效应的情形;其中，渗透率动态效应对探测半径的影响比压敏因素更显著。该研究对低渗致密气藏开发具有指导意义。

渗透率动态效应;压力敏感;数值离散;探测半径;水平井;致密气藏

0 引言

由于水平井能大幅增加储层渗流面积和控制程度［1-2］，因此被广泛地应用于鄂尔多斯盆地低渗致密气藏的开发中，而探测半径是评价水平井对气藏控制程度及井网部署的重要参数［3-4］。

在石油工业中，探测半径被定义为瞬时对地层施加一个压力波，某一时刻压力波传播位置与井的距离即为探测半径［5］。Matthews［6］、Slider［7］和Daungkaew［8］等基于油井控制储量推导了探测半径公式。然而，这些公式并不能解决大井径问题、短时问题和叠加问题。Gringarten等［9］根据压力导数曲线给出了探测半径的范围，但精度较低，不能满足实际要求。毛伟［10］以地层流量分布为基础得到探测半径公式，但地层流量难以测量，公式应用不方便;石军太等［11］基于压力分辨率推导出探测半径公式，但其会随着施工条件的变化而变化，难以推广。同时，这些研究都是针对直井，不适用于水平井。齐丽巍等［12］、朱黎鹞等［13］分别采用分形理论和虚拟直井方法建立了水平井的探测半径公式。但是，这些研究仅适用于常规油藏。低渗致密气藏存在渗透率动态效应和压力敏感现象［14］，而在考虑渗透率动态效应和压敏效应的探测半径方面，国内外鲜有报道。由于渗透率动态效应和压敏效应使得渗流方程具有较强的非线性，难以得到探测半径的解析解。因此，采用数值离散法对低渗致密气藏水平井的探测半径进行研究，希望能弥补这一不足，为鄂尔多斯盆地低渗致密气藏开发提供参考。

1 渗透率动态效应和应力敏感效应

1.1 渗透率动态效应

许多研究成果表明，低渗岩石流体渗流偏离达西定律。一些学者一般采用启动压力梯度［15-17］来表征这种非线性现象，然而对于启动压力梯度，存在许多争议［18］。在此，借鉴前人的研究［19］，利用渗透率动态效应来描述非线性现象，即认为渗透率K随压力梯度的变化而变化:

式中:KG为动态渗透率，10-3μm2;gradp为压力梯度，MPa/m;p为气藏压力，MPa。

气体拟压力被定义为:

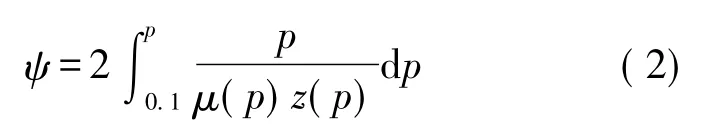
而气体的黏度和压缩系数通常被认为是常数，常采用地层平均压力下的数值［20］，则:

对于一般气藏来说，式(3)成立，则式(2)可得:

将式(4)代入式(1)，可得到气藏渗透率与拟压力之间关系:

式中:Ψ为气藏拟压力，MPa2/mPa·s;gradΨ为拟压力梯度，MPa2·(mPa·s)-1·m-1;μ为气体黏度，mPa·s;z为气体压缩因子;为平均气体黏度，mPa·s;为平均气体压缩因子。

1.2 应力敏感效应

在气藏开发过程中，随着地层压力不断下降，岩石有效应力不断增加，导致渗透率逐渐降低。在此过程，可认为渗透率是压力的指数函数［21］:

根据式(2)和式(3)，并利用无量纲渗透率系数KD表示Kp/K0，则:

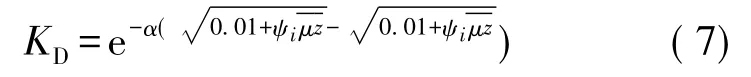
可得到无量纲渗透率系数与拟压力之间关系:

式中:Kp为压力敏感下渗透率，10-3μm2;K0为某一有效应力下渗透率，10-3μm2;pi为初始气藏压力，MPa;p为开发过程气藏压力，MPa;α为介质变形系数;Ψi为地层初始气体拟压力，MPa2/mPa·s。

2 水平井渗流模型

2.1 物理模型

渗流力学模型如图1，基本假设如下:水平井位于均质低渗致密气藏中心;气体流动方式为达西流;考虑井储和表皮效应;考虑渗透率动态效应和应力敏感效应;忽略毛管力和重力影响;渗流过程为等温;气井以定产量进行生产。

图1 低渗致密薄层气藏水平井物理模型

2.2 保角变换

由保角变换原理可知，变换前后对应线段的势(压力波)不变，变化的仅是线段的长短和流动形式［22］。在变换过程中，忽略油井半径的影响。

假设气藏长轴为Lchξe，短轴为Lshξe，水平井半长为L。则:

根据式(9)，将Z平面的椭圆形变成W平面上矩形，长为ξe，宽为ξ，如图2。经过保角变换后，水平井的椭圆流变为W平面的单向流。其中，蓝色线段表示水平井，红色虚线表示压力波位置。

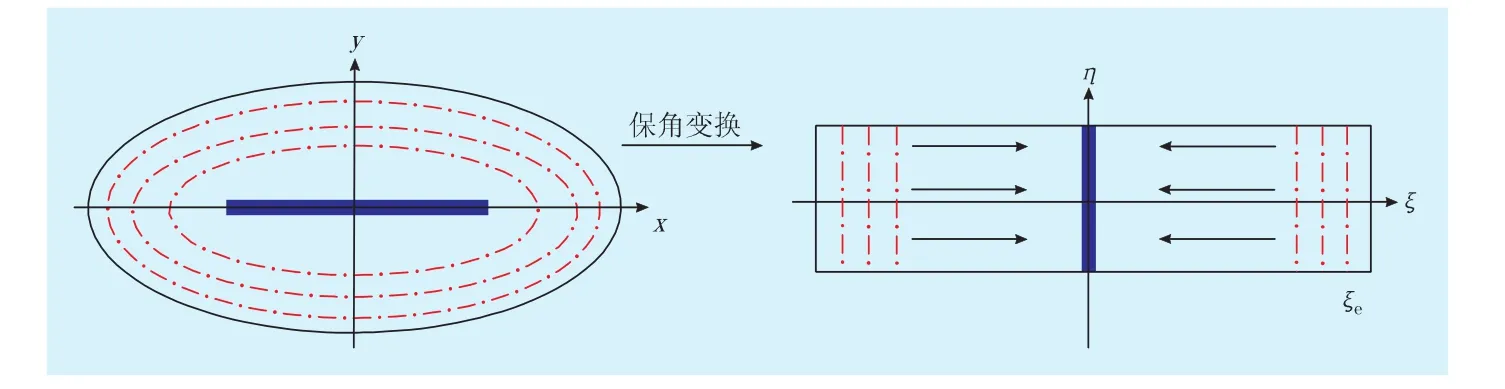
图2 水平井保角变换示意图

利用面积等效原理，将椭圆等效为圆，则等效探测半径为:

式中:L为水平井半长，m;r为等效探测半径，m;ξ为保角变换后矩形地层横坐标，m。

2.3 数学模型

在W平面上，由连续性方程、运动方程和状态方程可得到如下数学模型:

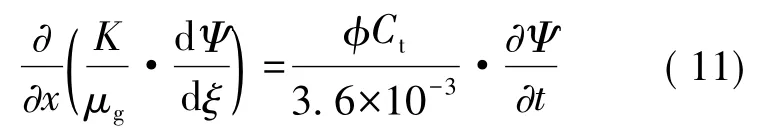
为简化计算，认为渗透率动态效应和压力敏感效应影响是相互独立的，则:

则式(11)可化为:

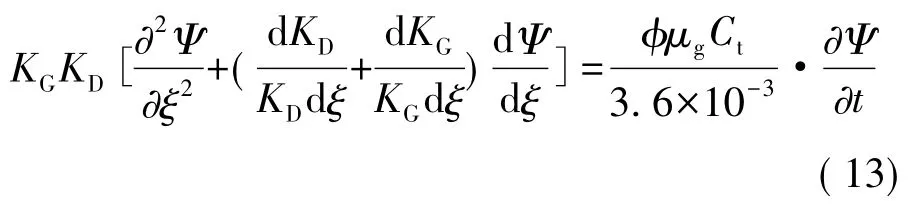
初始条件:

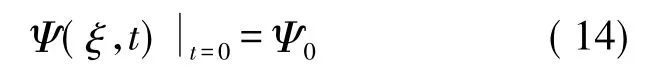
外边界条件:

内边界:

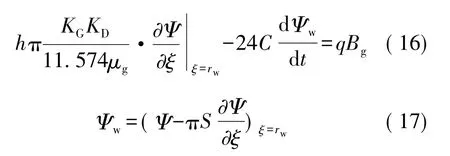
式中:Ψw为井底拟压力，MPa2/mPa·s;Ψ0为原始致密气藏拟压力，MPa2/mPa·s;KG表示动态渗透率，与拟压力梯度有关，10-3μm2;KD表示压敏因素影响下无量纲渗透率系数;t为生产时间，h;φ为孔隙度;Ct为气层综合压缩系数，MPa-1;μg为气体黏度，mPa·s;rw为气井半径，m;h为气层厚度，m;C为井筒储集系数，m3·d-1·MPa-1;S为表皮系数; q为气井产量，m3/d;Bg为气体体积系数，m3/m3。

3 模型求解

采用数值方法对式(13)～(17)进行离散，可得到1个对角占优的三对角矩阵，利用追赶法可求解出任意时刻气层拟压力分布情况，并得到矩形地层拟压力波传播的距离，利用式(10)，便可得到低渗致密气藏水平井探测半径。其求解过程如下。

(1)确定渗透率K与拟压力梯度、拟压力的曲线关系，为迭代计算做准备。

(2)对于KG与KD的处理方法。若拟压力与拟压力梯度位于离散曲线之间，则采用插值法计算。

(3)对数学模型进行离散，确定时间步长和距离步长，对模型进行求解:①载入初始数据;②利用初始数据计算出气藏拟压力分布，由拟压力分布得到KD分布;③由气藏拟压力分布计算拟压力梯度分布，由拟压力梯度分布得出KG分布，并认为拟压力梯度等于0处为探测边界;④将KD和KG代入模型中，准备计算气藏的拟压力分布;⑤循环②～④，记录时间和距离;⑥迭代时间为探测时间，对应距离为探测半径。

4 实例计算

4.1 基本参数

以鄂尔多斯盆地2种不同物性的低渗致密气藏1和气藏2为例，其KD与拟压力Ψ的关系曲线、KG与拟压力梯度gradΨ的关系曲线如图3所示，其他参数一致:地层厚度为10 m，原始地层压力为31.8 MPa，水平井表皮因子为-0.6，水平井产能为10 000 m3/d，气体黏度为0.01 mPa·s，气体压缩因子为0.95，地层综合压缩系数为0.000 5 MPa-1，地层孔隙度为0.012，水平井半径为0.1 m，水平井半长为400 m，井储系数为0.08 m3/(d·MPa)。

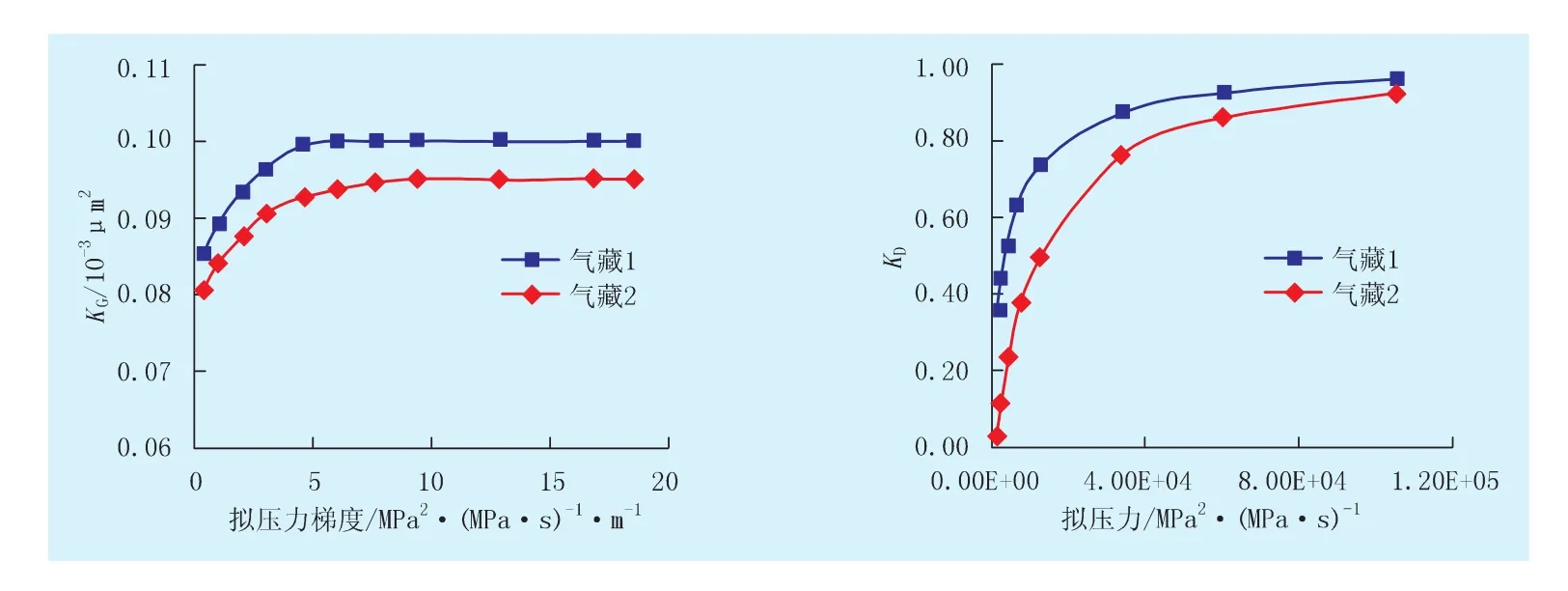
图3 KG、KD分别与拟压力梯度、拟压力的关系曲线

4.2 不同情况下的水平井探测半径数值解

图4分别是气藏1和气藏2在4种不同情况下水平井探测半径的数值解(基本参数一致):考虑动态渗透率和压力敏感效应;只考虑动态渗透率效应;只考虑压力敏感效应;不考虑动态渗透率和压力敏感效应。

图4 低渗致密气藏在不同情况下水平井探测半径与时间的关系

由图4可以看出，动态渗透率和压力敏感效应的存在都会减小水平井的探测半径，因为压力波在地层传播时，动态渗透率和压力敏感效应会使气层渗透率变小，降低了拟压力波在气层的传播速度，进而减小水平井探测半径，使水平井探测半径曲线下弯，这与实际情况相符。

同时，应力敏感效应对探测半径的影响较渗透率动态效应弱。因为拟压力波在气层传播速度较快，当达到某位置时，拟压力变化很小，岩石变形可忽略，KD接近于1，即压敏效应对水平井探测半径影响较小。

4.3 水平井探测半径拟合

目前，由于理论上的不完善，探测半径计算公式缺乏统一和规范性，但探测半径可以用通式xi=(η为压力传导系数)来表示，只是不同的学者研究得到了不同的系数C［23］。

图5 水平井探测半径拟合曲线

考虑动态渗透率和压力敏感效应，分别对气藏1、2的水平井探测半径曲线进行数学拟合。如图5所示，气藏1的曲线拟合结果为C=1.23;气藏2拟合结果为C=1.27，C值为1.2～1.3，而未考虑渗透率动态效应和压敏效应时，C值为，这进一步说明了动态渗透率效应和压力敏感效应会减小探测半径。

5 结论

(1)建立了动态渗透率和压力敏感效应下水平井渗流模型，以鄂尔多斯盆地致密气藏为例，采用数值离散法，得到其探测半径与时间的关系曲线，并与只考虑动态渗透率效应、只考虑压力敏感效应、不考虑动态渗透率和压力敏感效应下的曲线进行对比。

(2)动态渗透率和压敏效应会减小水平井探测半径，使探测半径曲线下弯。其中，动态渗透率效应对水平井探测半径的影响比压敏效应更显著。因此，研究低渗致密气藏水平井探测半径时，需重点考虑动态渗透率效应。

(3)对动态渗透率和压敏效应下水平井探测半径曲线进行数学拟合，系数C值为1.2～1.3，比一些学者的研究结果偏小，究其原因，是因为考虑动态渗透率和压力敏感效应，其会使气层渗透率变小，降低了拟压力波在地层的传播速度，进而减小探测半径。

［1］吕志凯，冀光，位云生，等.致密气藏水平井产能图版及应用［J］.特种油气藏，2014，21(6):105-108.

［2］陈元千.辐射状分支水平井产能公式研究进展［J］.特种油气藏，2014，21(1):1-6，11.

［3］王刚，戴卫华，段宇.压力恢复试井探测半径计算新方法［J］.中国海上油气，2014，26(5):55-57.

［4］陈志明，廖新维.探测半径的计算公式［J］.油气井测试，2014，23(5):5-9.

［5］Van Poollen H R.Radius-of-Drainage and Stabilization-Time Equations［J］.Oil and Gas Journal，1964，62(4): 138-164.

［6］Matthews C S，Russell D G.Pressure Buildup and Flow Tests in Wells［C］.Monograph Series，Society of Petroleum Engineers of RIME，Dallas，1967.

［7］Slider H C.Worldwide Practical Petroleum Reservoir Engineering Methods［C］.Tulsa，Oklahoma，Penn Well Publishing Co，1983.

［8］Daungkaew S，Hollaender F，Gringarten A C.Frequently Asked Questions in Well Test Analysis［C］.SPE63077，2000.

［9］刘能强.实用现代试井解释方法［M］.北京:石油工业出版社，2008:66-68.

［10］毛伟.基于流量的探测半径计算方法研究［J］.油气地质与采收率，2006，13(1):77-78.

［11］石军太，李相方，李乐忠，等.考虑压力计分辨率的探测半径公式［J］.油气井测试，2012，21(2):8-10.

［12］齐丽巍，王晓冬.探测半径计算方法研究［J］.油气井测试，2007，16(2):1-3.

［13］朱黎鹞，童敏，闫林.水平井探测半径及其计算方法［J］.天然气工业，2010，30(5):55-57.

［14］姚军，刘顺.基于动态渗透率效应的低渗透油藏试井解释模型［J］.石油学报，2009，30(3):430-433.

［15］陈志明，蔡雨桐，刘冰，等.低渗透岩石渗流规律的实验研究方法［J］.天然气与石油，2012，30(3):49-52.

［16］张楠，王晓琴，徐锋，等.启动压力梯度和应力敏感效应对低渗透油藏直井产能的影响［J］.特种油气藏，2012，19(1):74-77.

［17］熊健，王绍平，郭平.低渗油藏水平裂缝井增产规律研究［J］.特种油气藏，2012，19(6):101-103.

［18］李传亮.启动压力梯度真的存在吗?［J］.石油学报，2010，31(5):867-870.

［19］郑春峰，程时清，李冬瑶，等.低渗透油藏通用非达西渗流模型及压力曲线特征［J］.大庆石油地质与开发，2009，28(4):60-63.

［20］Wattenbarger，Robert A，Ramey J R.Gas well testing with turbulence，damage and wellbore storage［J］.Journal of Petroleum Technology，1968，20(8):877-887.

［21］许涛，黄海龙，修德艳，等.低渗透油藏应力敏感评价新方法［J］.特种油气藏，2014，21(6):126-129.

［22］Chen Z M，Liao X W，Zhao X L.Productivity estimations for vertically fractured wells with asymmetrical multiple fractures［J］.Journal of Natural Gas Science and Engineering，2014.21(6):1048-1060.

［23］Hsieh B Z，Chilingar G V，Lin Z S.Propagation of Radius ofInvestigation from Producing Well［J］.Energy sources，2007，29(5):403-417.

编辑黄华彪

TE33

A

1006-6535(2015)05-0090-05

20150412;改回日期:20150803

国家重点基础研究发展计划“陆相致密油高效开发基础研究”(2015CB250905);国家自然科学基金“超低渗透油藏注气提高采收率理论与技术研究”(U1262101);教育部高等学校博士学科点专项基金项目(新教师类)“CO2驱渗流机理及理论模型研究”(20120007120007)

陈志明(1989-)，男，2013年毕业于长江大学石油工程专业，现为中国石油大学(北京)油气田开发工程专业在读博士研究生，从事油气渗流理论方面的研究工作。

10.3969/j.issn.1006-6535.2015.05.019