遗传算法优化模块度的二分网络社团检测方法

卜振兴，　洪卫军

(中国人民公安大学， 北京　100038)

遗传算法优化模块度的二分网络社团检测方法

卜振兴，洪卫军

(中国人民公安大学， 北京100038)

摘要目前二分网络社团检测研究处于探索阶段，评估标准和检测方法较少，模块度值具有局部性且偏差较大，检测结果不稳定。针对上述问题，提出一种基于遗传算法优化二分网络模块度的检测方法，依据节点相似度初始化染色体，通过不断改变社团个数，使用改进的遗传算法交叉、选择和变异等因子，遗传迭代获得全局模块度最大值以及对应的社团划分。仿真结果表明：能够有效检测到模块度全局最大值以及对应的社团个数和社团划分，社团划分更加精准，算法具有较强的鲁棒性和抗干扰能力。

关键词复杂网络； 二分网络； 遗传算法； 社团结构

0引言

复杂网络是一种具有自组织、自相似、吸引子、小世界、无标度中部分或者全部性质的网络。简而言之，复杂网络呈现了高度的复杂性。

社团结构特性是复杂网络中一种介于宏观和微观之间的重要性质，其典型特征表现为：社团内部节点之间的联系较为密切，而社团与社团之间节点的联系相对较少。社团检测是通过一些算法检测出网络的社团划分，是分析复杂网络的前提和基础，引起了各个领域研究学者的极大兴趣和广泛关注。目前已经有了很多检测社团结构的方法，这些方法使得人们在分析各种信息网络、生物网络以及社会网络等的社团结构时更加准确有效，分析的网络规律也越来越大。

二分网络是具有两种节点类型的网络，节点关系仅存在于不同类型节点之间，同类型节点之间不存在联系，如：科学家- 论文、人员- 位置等网络都是典型的二分网络，生活中普遍存在形形色色的二分网络，研究二分网络可以了解和解释网络的内部特征，掌握节点之间的规律，同时可以应用于实际。例如：通过分析一个人出现的地点，可以掌握该人的活动规律；分析一种犯罪的特征，可以挖掘出该类案件的犯罪群体等。因此，研究二分网络不仅具有重要的理论意义，更具有广泛的现实意义，成为学者研究的重点和热点。

二分网络社团检测最初基于映射法来实现，将二分网络转换为单分网络，使用较为成熟的单分网络检测方法进行检测。随着科学的发展，不少学者提出了直接检测法，即直接使用二分网络模型进行检测，如：Guimera等人提出了二分模块度，设计出对应的检测方法，但是该方法只能每次检测一种类型的节点；Barber对Newman单分模块度进行了拓展，提出自己的二分网络模块度及对应的二分网络检测方法BRIM。虽然上述两种方法都各具优点，但都存在着一些问题和难点，使得检测结果准确性不够。其难点可以归纳为：(1)映射法的映射方法不够精准，造成重要信息丢失，从而使得检测结果存在误差，如何设计一种更精准的映射方法是该类方法的难点；(2)非映射法由于检测模型不够准确和需要额外初始输入，使得检测结果局部最优，如何找到全局最优检测方法是此类检测方法的难点。

为了克服上述问题和难点，本文提出一种新型的基于遗传算法优化二分网络模块度的社团检测方法，为了得到全局最大模块度值，最初不限定社团个数，检测划分不同社团个数时的模块度局部最大值，逐步改变社团个数，得到全局最大模块度值。在每次检测中，根据网络节点对的相似度，得到节点相似度矩阵，根据矩阵初始化染色体，通过遗传操作得到局部最大值以及对应的社团划分结果。

本文方法具有以下优点：(1)无需额外输入参数，通过不断改变社团个数，检测全局模块度最大值及对应的网络划分结果；(2)根据单分加权网节点相似度初始化染色体序列，避免由于映射信息丢失造成误差较大的问题；(3)根据实际要求单独检测某一类型节点的社团划分，避免同时计算两类节点造成的冗余计算，节省算法时间，提供计算效率。

1二分网络相关原理

1.1　二分网络概念

二分网络是复杂网络中的一种重要表现形式，相对于单分网络(节点类型唯一的网络)，二分网络由两部分不同类型网络节点构成，同一类型网络节点不相连，关系仅存在于不同类型节点之间的网络，如图1。

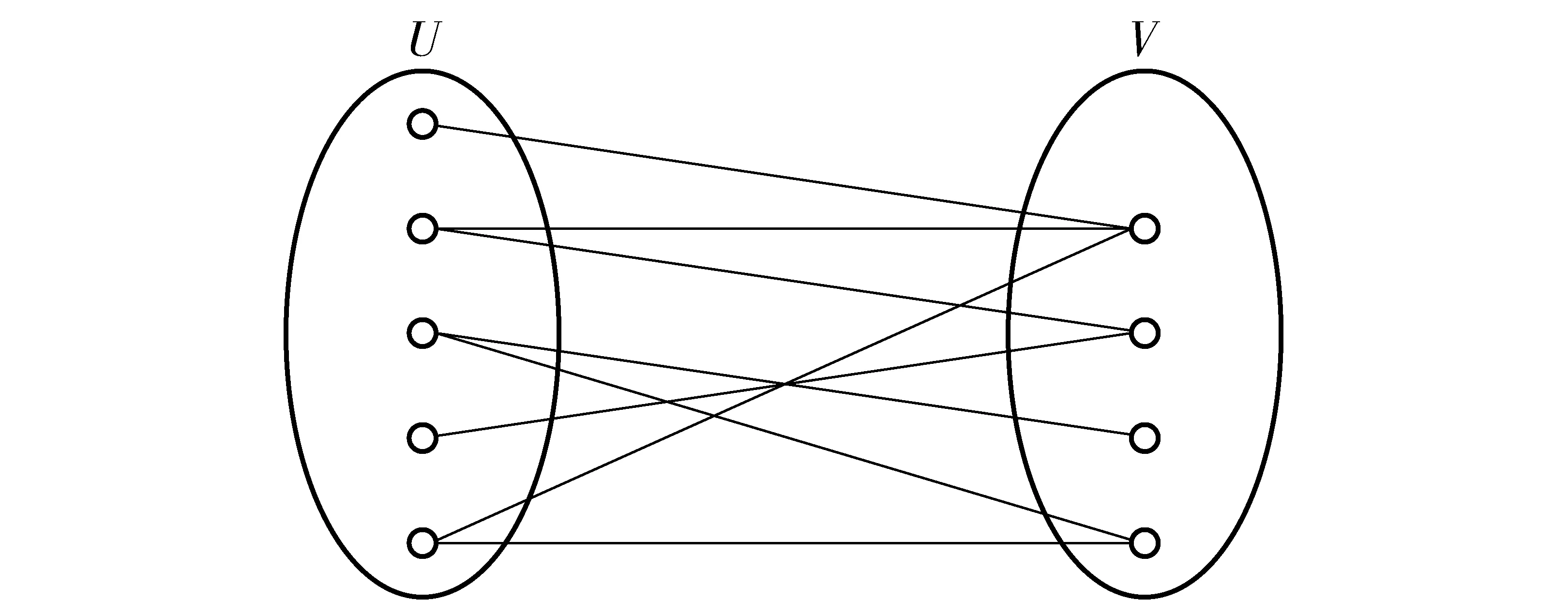
图1　二分网络模型

1.2　节点相似度

节点相似度，即为节点对之间的相似程序，在社团网络中，一般按照他们的社会圈的相似性来定义顶点的相似性。例如：两个人共同的朋友数。在理论网络中，一般定义为两个节点具有共同边的个数，假如节点a和b，存在共同的连接节点集合N，那么N中个数数量越大，说明节点A和B的相似度越高，反之，相似度越低。目前，常用的计算节点对相似度的公式有：

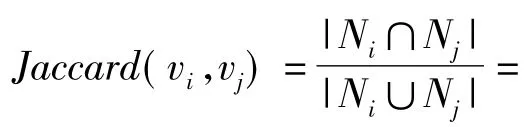
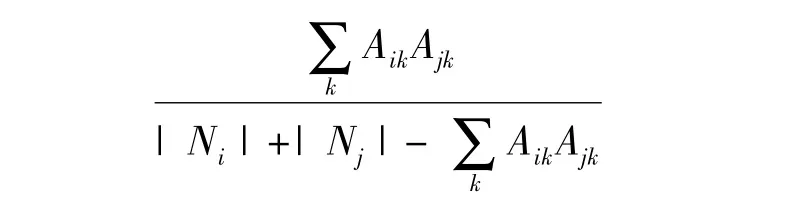
(1)

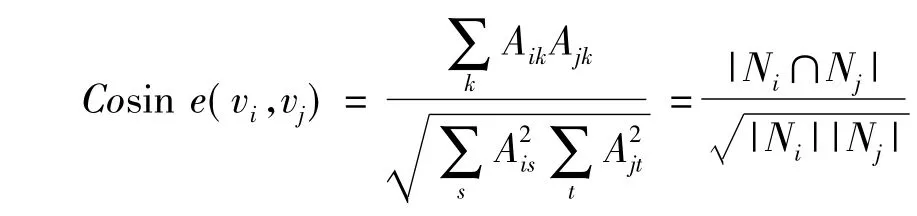
(2)

在上面的公式中，Ni表示节点vi的邻域，|*|表示集合的势，即元素个数。两种相似度的取值范围都介于0~1之间。

1.3　二分网络模块度

模块度Q是由Newman等人为解决衡量复杂网络中社团划分质量提出的一种衡量标准，Q值越大，表明该网络具有的社团结构越明显，Q的取值范围为[0,1]，在实际网络中，该值范围通常介于0.3~0.7之间。

在单分网络中，我们假设网络可以划分为k个社团，M定义为网络中边的数量，V定义为网络中所有节点的集合，Vi和Vm定义为两个社团，A为网络的邻接矩阵。那么我们可以定义θim为社团Vi到社团Vm的所有连接占整个网络边的比例。

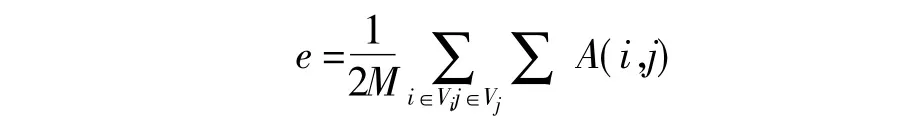
(3)

我们进一步定义大小为kk的矩阵E，其中E中元素表示为eij，矩阵中每行的和定义为ai:

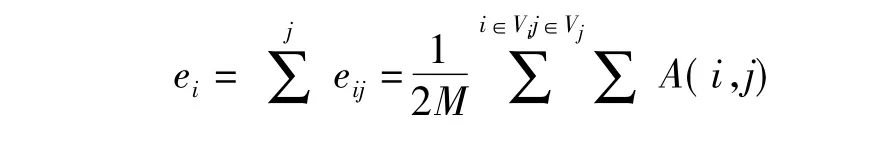
(4)

在网络中，当不考虑定点所属的社团，在保持网络节点度序列不变的情况下，进行随机连接时，我们可以得到eij=aiaj因此，网络模块度Q可以表示为：

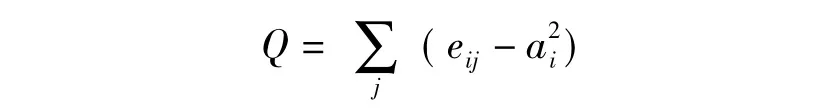
(5)

给定一个网络划分时，假设网络划分为k个社团，我们建立一个k*k的邻接矩阵E，其中eij表示节点分别处于社团i和j的边占网络总边的比例，eij表示位于同一社团i内的边占网络总边数的比例，ai表示的是在保持网络节点度序列不变的情况下，边进行随机连接后得到的网络中社团i的内部边数占总边数的比例的期望值。一般来说，Q值越大，对应的社团结构越明显，目前大家公认的是如果网络的划分具有的最大Q值大于0.3，表明该网络具有明显的社团结构。

目前，对于单分网络模块度研究较为成熟，二分网络模块度尚处于探索阶段，Guimera和Barber分别推广和拓展了Newman的单分模块度得到自己的二分网络模块度公式。Guimera的二分网络模块度表示为：

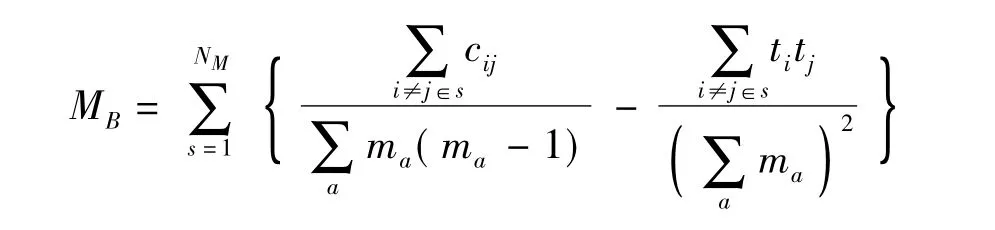
(6)

其中，X和Y是类型节点集合，s是X类节点的一个社团，NM的X类节点的社团个数，a是Y类节点的一个社团，ma是连接社团a中的边的个数，cij是Y类节点的社团个数，节点i和j是连通的，ti和tj分别是Y中连接到节点i和j的社团总数。

Barber的二分网络模块度表示为：

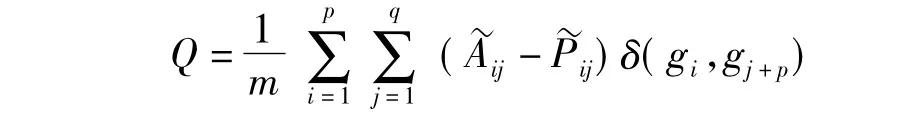
(7)

其中，A为二分网络的邻居矩阵，0i×j是i行j列全零矩阵，P为网络对应随机模型的连接概率期望矩阵，所谓随机网络模型下的连接概率定义为网络中随机生成一条连接指定顶点的概率。

1.4　二分网络常用检测方法分析

目前常用的二分网络社团检测方法大致分为两种：映射法和非映射法。

映射法首先将二分网络映射为传统的单分网络，然后使用较为成熟的单分网络社团检测方法进行社团结构划分如图2。

图2　二分网络映射为单分网络

该方法的优点是实现简单且较为成熟，缺点是在单分映射过程中会丢失一些重要的网络信息，无法保证划分的严谨性。因此，如果能找到一种方法使得在映射过程中尽量保留原本信息，则可以更加有效、精准地检测出二分网络社团结构。

非映射方法即直接在原始网络上划分社团结构，可以最大程度上保留原有网络的信息。目前常用的非映射法主要是基于Barber的BRIM，但该方法仅适用于检测小型二分网络，且在检测初始阶段需要额外的输入，使得在检测应用时有较大的局限性。

2遗传算法优化二分网络模块度检测方法

为了克服以往算法的缺点和局限性，得到全局模块度Q最大值，本文使用改进的遗传算法，在不断改变社团个数的情况下，通过遗传算法优化二分网络模块度Q值，获得模块度全局最大值，从而得到更加有效精准的社团划分。

2.1　算法总体框架

本算法主要涉及到群体编码及初始化、适应度的评价、选择算子、交叉算子、变异算子等概念。本文提出来的二分网络社团检测方法，是以二分网络模块度为优化函数，使用遗传算法对二分网络模块度Q最为适应度函数，通过选择、交叉和变异操作进行优化，以求得最大值检测社团结构，该算法的基本框架为：

准备工作：将二分网络映射单分无向加权网，得到对应矩阵，并计算节点对的相似度；

输入：无向加权网对应矩阵，节点对相似度；

输出：模块度最大值Q及其对应的社团划分。

算法主要步骤：

(1)初始化与编码。进化代数计数器t=0，最大进化代数T，初始社团个数k=2，最大社团个数K(默认为节点个数)，根据节点相似度生成M个染色体作为初始群体P(t)；

(2)计算群体P(t)中每个个体的适应度值Q；

(3)选择运算。根据pi=Qi/∑Q计算每个个体概率分布，通过生成范围[0,1]的均匀随机数s，将s作为选择指针确定被选个体；

(4)交叉运算。通过生成范围[0,1]的均匀随机数c，若c小于交叉概率pc，选择两个个体进行交叉操作；

(5)变异运算。随机生成范围[0,1]的随机数m，若m小于变异概率pm，则随机选取某一位置进行变异。群体P(t)经过选择、交叉和变异操作后，产生新一代群体P(t+1)；

(6)遗传终止条件判断。若t=T，则进化结束，取遗传过程中Q最大值的个体作为局部最优结果；否则，继续从2)开始；

(7)算法终止条件判断。若k达到最大值K，则整个算法终止，取局部最优结果最大值对应的社团个数k和划分最为结果输出；否则，重新设置k的值，继续从1)开始遗传操作。

2.2　初始化与编码

编码是遗传算法中最基本的一步操作，针对复杂网络社团检测问题，编码即将社团按照序号从小到大进行编号，将不同的节点对应到不同的序号，表示该节点属于某个序号的社团。具体的染色体编码如图3所示。

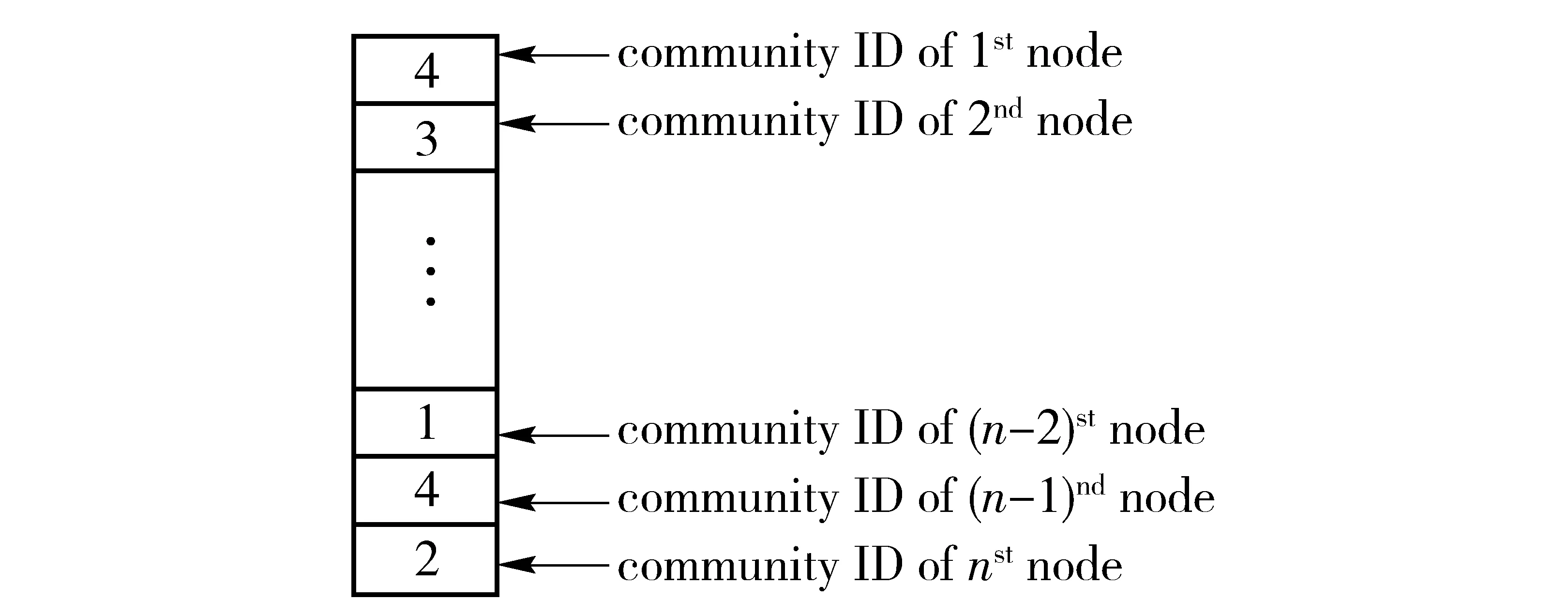
图3　染色体编码

染色体的长度取决于节点的个数，染色体的编码代表每个节点所属的社团编号。如图中所示，第一个节点和最后一个节点分别属于编号为4和2的社团。

初始化的过程是将每个染色体节点随机分配一个社团ID，为了避免无效划分，尽可能得到最优解和减少迭代次数，在本文初始化过程中，我们加入一些约束条件，即节点之间联系密切的节点对尽可能分配同一社团ID，对于不存在任何联系的节点，可以随机分配一个社团ID。

在本文的初始化过程中，我们首先将二分网络映射为单分加权网络，使用单分网络节点相似度函数计算二分网络节点对的相似度，根据将节点相似度大的节点尽可能分配同一社团ID。本文采用Jaccard公式1计算单分网络节点对的相似度，得到节点相似度矩阵。

2.3　个体适应度计算

使用单分网络模块度Q原理，推导二分加权网络模块度Qw，使用Qw计算每个个体的适应度值，作为评价社团划分质量的标准。

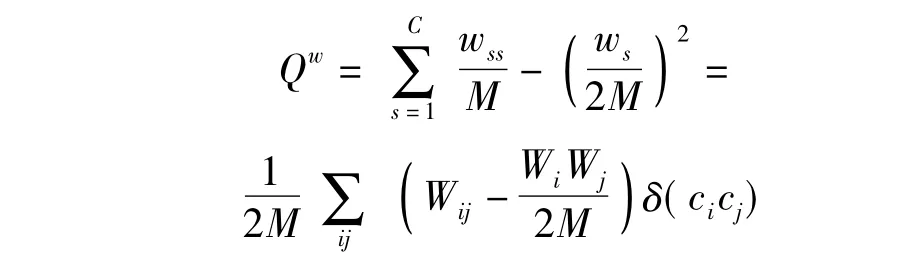
(8)

公式(8)中，W为单分加权网络的邻接矩阵，其中元素W为节点之间权值，当节点之间存在连接，则Wij>0，否则Wij=0。

2.4　选择运算

遗传算法的原理从本质上说基于达尔文的自然选择学说。选择提高了遗传算法的驱动力。Holland提出的轮盘选择是最为知名的选择方式，其基本原理是根据每个染色体适应值的比列来确定该个体的选择概率或者保留概率。因此，在每一代种群中，根据适应度函数，计算每个染色体(即每个个体)的适应度概率，根据适应度概率进行排序，通过建立一个轮盘模型来表示这些概率。选择的过程就是旋转轮盘若干次(次数等于社团的个数)，每次为新种群选出一个个体作为优秀个体参与下一代的遗传操作。轮盘这种选择方法的特点就是随机采样过程。

2.5　交叉运算

交叉算子根据交叉概率将种群中的两个染色体随机交换部分基因产生新的染色体，期望将有益基因组合在一起。目前，最常用的交叉运算是单点交叉，所谓单点交叉，即在染色体中随机设置一个交叉点，互换该点前或后的个体对的部分结构，从而产生新的个体对。在本算法过程中，染色体上的每个节点代表该节点所属的社团，为了防止交叉过程中，出现父代信息的丢失，本文交叉采用单向交叉，即个体A、B交叉过程中，A中的某些节点替换B中的相应节点，A中节点内容保持不变，如图4所示。

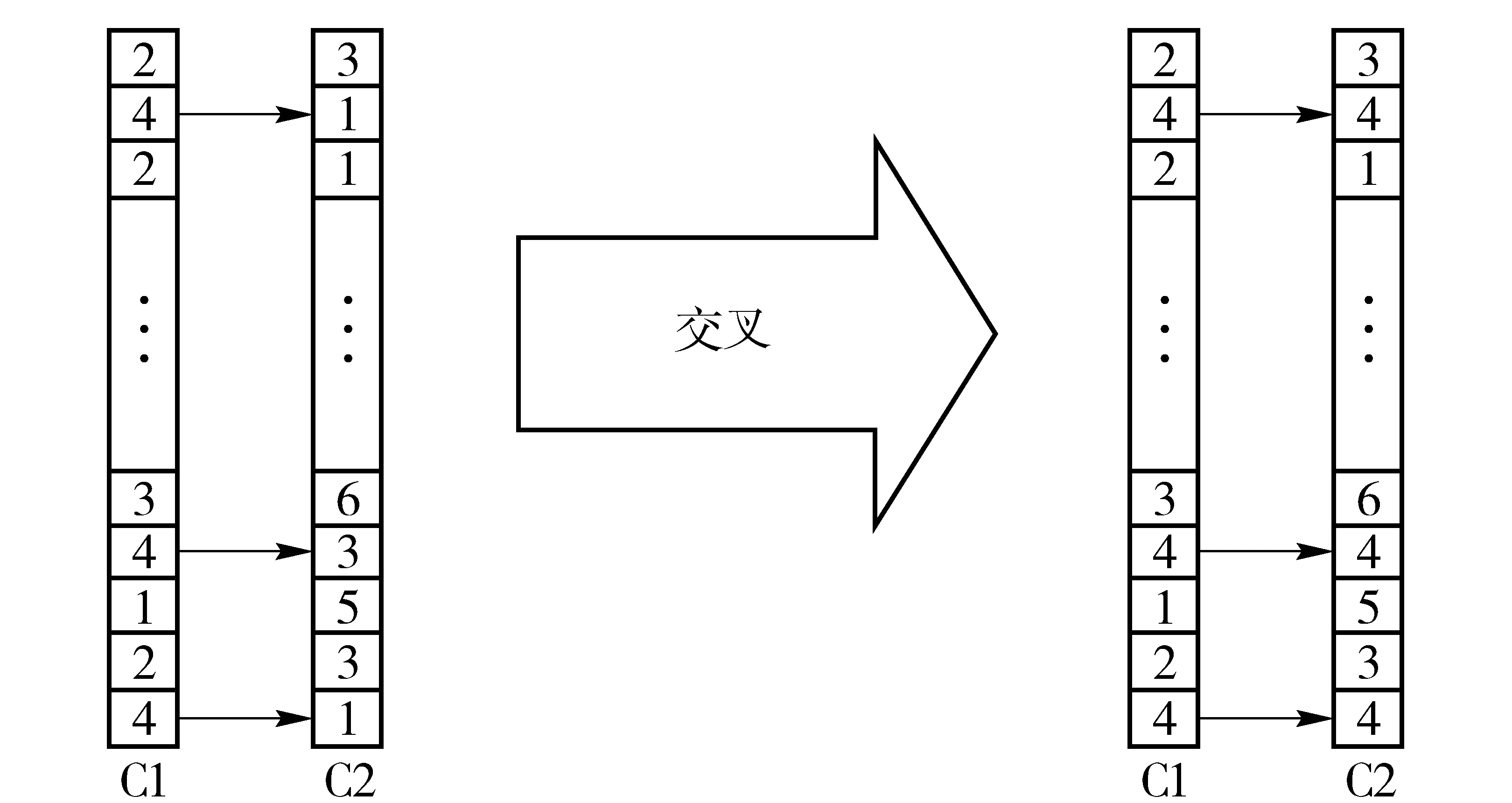
图4　交叉算子

2.6　变异运算

变异同交叉一样，也是遗传算法中的核心内容。所谓变异，即单个个体是遗传过程中，由于环境等某些原因，造成个体自己上的某些节点以变异概率Pm发生变异。随机生成范围[0,1]的随机数m，若m小于变异概率pm，则随机选取某一位置进行变异。至此，产生新一代群体P(t+1)。

3仿真结果与分析

为了验证本算法的有效性，将本算法应用于在数据集Southern Women Data上对本文算法进行试验分析。本文所有实验均在Windows环境下，使用matlab7编程计算和绘图。

美国南部Davis俱乐部数据是由Stephen提出的一个美国妇女参与活动的二分网络，该网络由18位妇女和14个活动组成，节点代表妇女，边代表妇女参与的活动。

在本实验中，染色体的长度设置为妇女总数18，并根据节点对之间的相似度和社团个数进行编码，初始化社团个数为2个，遗传代数为20次，随机生成20个个体做为遗传群体，交叉概率设为0.6，变异概率设为0.002。对于不同的社团个数，得到的最优结果是不确定的，因此本实验从划分2个社团开始，逐步增加社团的个数，从中选择使得模块度最大的作为最优解。

在该二分网络中，每个活动节点的度中心性排列见表1。

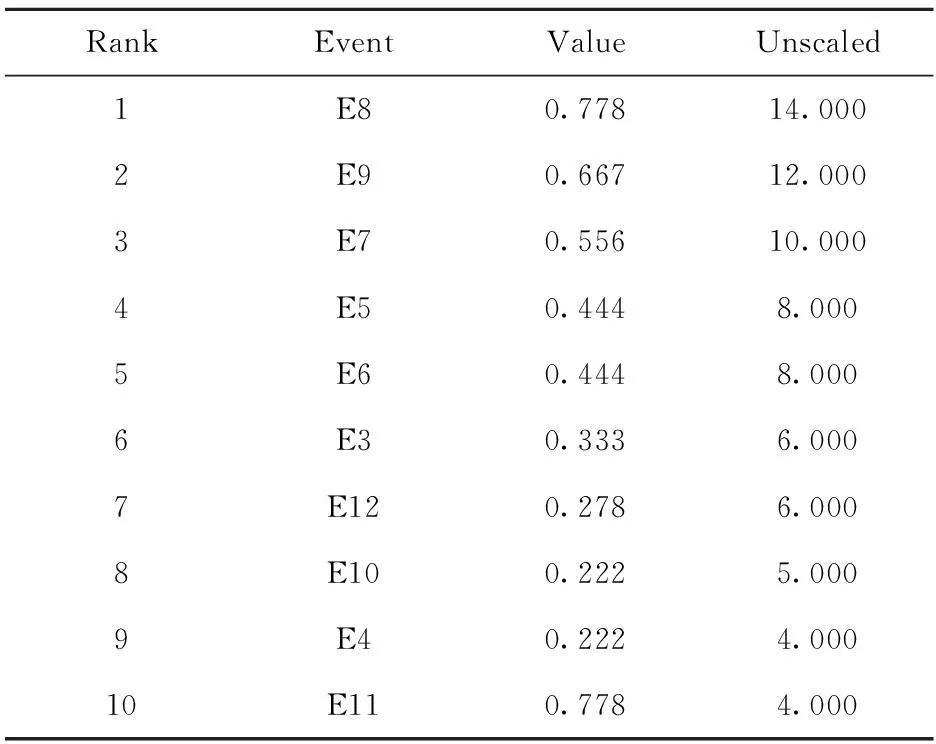
表1　In-degree centrality

每个妇女节点的度中心性排列见表2。

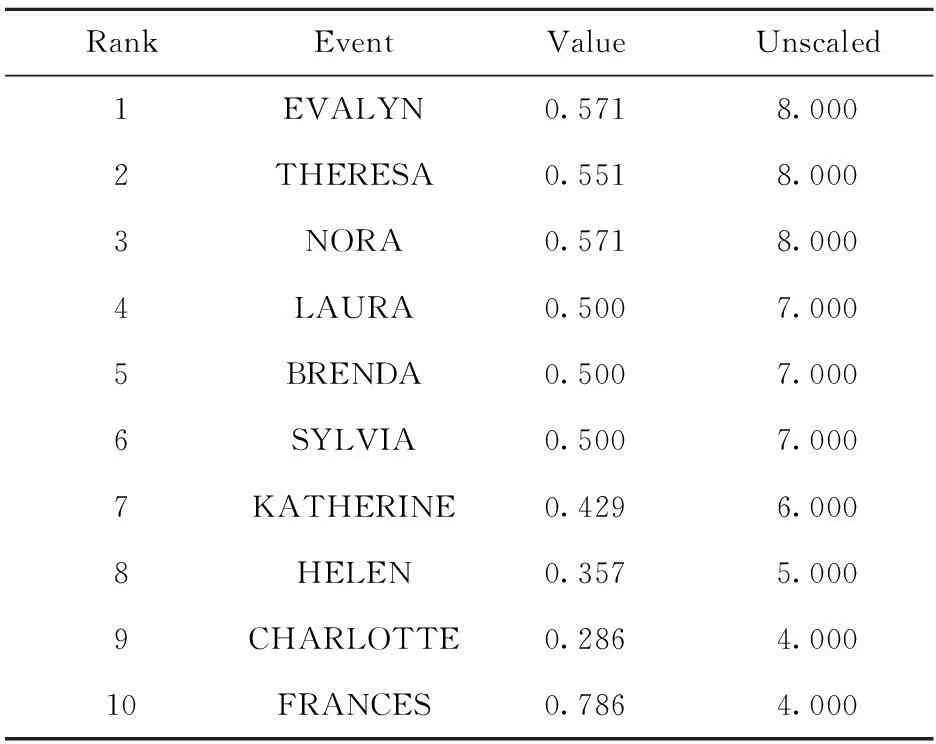
表2　Out-degree centrality

运用本文的遗传算法优化二分网络模块度方法对南部妇女Davis数据进行社团结构划分，算法开始设置初始划分社团个数为2个，每次遗传迭代结束后，通过不断改变社团个数，得到对应的模块度Q值。算法流程如图5所示。

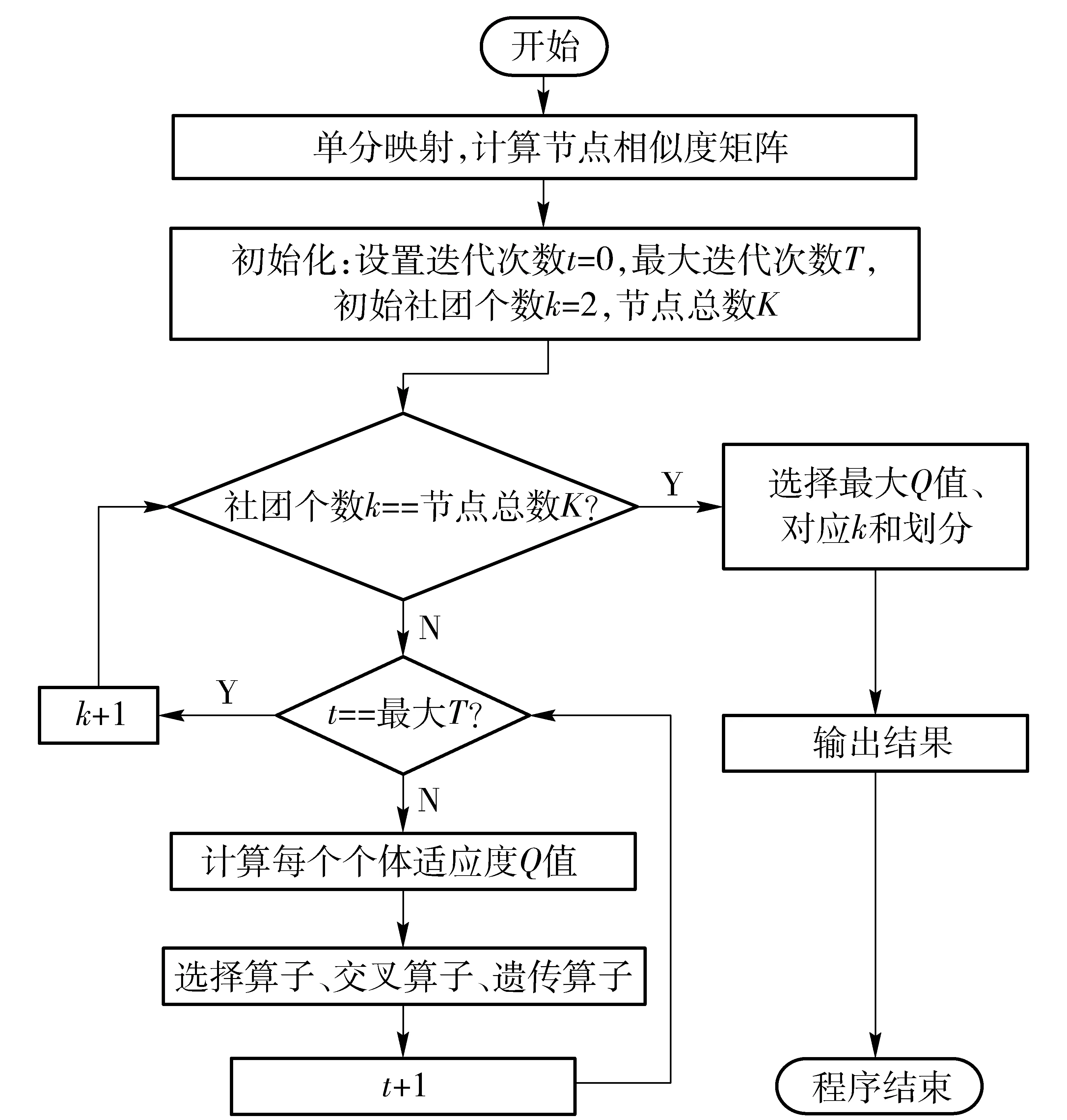
图5　本文算法流程图

结果显示：当网络被划分为2个社团时，模块度Q值最大约0.32，此时所有节点具有较好的社团结构如图6所示。

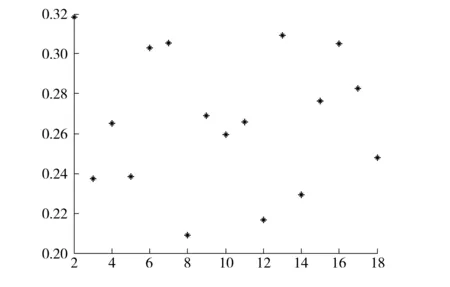
图6　Q随社团个数变化值

由图6可以看出：当模块度最大时，网络被划分为两个社团。其中红色节点代表妇女，蓝色节点代表参与的活动，其中红色妇女节点1~9被划分一个社团，红色妇女节点10~15被划分为一个社团，节点16~18由于跟其他节点连接较少，处于游离状态。该结果与使用Fast-Newman方法检测的结果相差无几，也进一步说明了本方法的有效性和准确性如图7。

图7　本文算法划分结果

为了进一步验证本算法的稳定性，对同一数据集重复20次仿真实验，仿真得到不同群体个数对应的Q均值与单次仿真曲线图拟合程度较高。

综合仿真实验结果表明：本文算法在单次仿真实验中得出的结果较之以往算法更加精准，多次重复仿真实验的结果与单次结果对比总体趋势相同。因此，本算法更加精准，具有较强的鲁棒性和抗干扰能力。

4结语

本文对复杂网络进行了详细的阐述，对二分网络相关原理进行了介绍，提出了基于改进的遗传算法和无向加权网络模块度划分二分网络的社团检测方法。目前对二分网络的社团检测大多基于单分网络，二分网络在转换为单分网络时，会因为一些数据的丢失造成社团检测分析出现误差，因此，直接基于原始二分网络的分析方法会成为后期研究的主要内容。

参考文献

[1]Girvan M, Newman M E J. Community structure in social and biological networks[J]. Proceedings of National Academy of the United States of America, 2002,99(12):7821-7826.

[2]Newman M E J, Grivan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004,69(2):026113.

[3]Guimera R, Ameral L A N. Functional cartography of complex metabolic networks[J]. Nature,2005,433(7028):895-900.

[4]White S, Smyth P. A spectral clustering approach to finding communities in graphs. 5th SIAM International Conference on Data Mining, Society for Industrial and Applied Mathematics, Philadelphia, 2005:274-285.

[5]Fortunato S, Barthelemy M. Resolution limit in community detection[J]. Proceedings of the National Academy of the United States of America, 2007,104(1):36-41.

[6]Sun Y, Danila B, Josic K, et al. Improved community structure detection using a modified fine-tuning strategy[J].Europhysics Letters, 2009,86(2), 28004.

[7]Good B H, DE Montjoye Y A, Clauset A. The performance of modularity maximization in practical contexts[J]. Physical Review E, 2010,81(4):046106.

[8]Li Z P, Zhang S H, Wang R S, et al. Quantitative function for community detection[J]. Physical Review E, 2008,77(3):036109.

[9]Wang G X, Shen Y, Ouyang M. A vector partitioning approach to detecting community structure in complex networks[J]. Computer & Mathematics with Applications, 2008,55(12):2746-2752.

[10]Ma X K, Gao L, Xuerong Y, et al. Semi-supervised clustering algorighm for community structure detection in complex networks[J]. Physical A: A Statistical Mechanics and its Applications, 2010,389(1):187-197.

[11]Newman M E J. Modularity and community structure in networks[J]. Proceedings of the National Academy of the United States of America, 2006,103(23):8577-8582.

[12]Newman M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E, 2004,69(6):066133.

[13]Fortunato S. Community detection in grahps[J]. Physics Reports, 2010,486(3):486-174.

[14]Fortunato S, Latora V, Marchiori M. Method to find community structures based on information centrality[J]. Physical Review E, 2004,70(5):056104.

[15]Radicchi F, Castellano C, Cecconi F, et al. Defining and identifying communities in networks[J]. Proceedings of the National Academy of the United States of America, 2004,101(9):2658-2663.

[16]Duch J, ARENAS A. Community detection in complex networks using extreme optimization[J]. Proceedings of the National Academy of Sciences of the United States of America, 2005,72(2):027104.

[17]Newman M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review E, 2006,74(3):036104.

[18]Rosvall M, Bergstrom C T. A information theoretic framework for resolving community structure in complex networks[J]. Procceedings of the National Academy of the United States of America, 2007,104(18):7327-7331.

[19]Palla G, Dermyi I, Farkas I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005,435(7043):814-818.

[20]杨树忠. 复杂网络中的社团检测问题研究[D]. 北京：北京交通大学, 2009, 3-4.

[21]Scott J. Social network analysisc: a handbook[M]. London: Sage Publications, 2000, 113-152.

[22]Clauset A, Newman M E J, Moore C. Finding community structure in very large networks[J]. Physical Review E, 2004, 70(6):066-111.

[23]Boccaletti S, Latora V, Moreno Y, et al. Complex networks:structure and dynamics[J]. Physics Reports, 2006, 424(4):175-308.

[24]Ergun G. Human sexual contact network as a bipartite graph[J]. Physica A, 2002, 308:483-488.

[25]Newman M E J. Finding community strcture in networks using the eigenvectors of matrices. Physical Review E, 74:036104, 2006.

[26]Newman M E J. Detecting community structure in networks. The European Physical Journal B, 2004,38(2):321-330.

[27]Guimera R, Sales-pardo M, Amaral L A. Module identification in bipartite and directed network[J]. Physical Review E, 2007,76:036102.

[28]Barber M J. Modularity and community detection in bipartite networks[J]. Physical Review E, 76, 066102, 2007:1-9.

[29]Li Zhen ping, Zhang Shi hua, Wang Rui sheng, et al. Quantitative function for community detection[J]. Physical Review E, 2008, 77(3):109-117.

[30]Newman M E J. Fast algorithm for detecting community structure in networks. Physical Review E, 69, 066133(2004).

[31]Palla G, Barabasi A-L, Vicsek T. Quantifying social group evolution. Nature, 2007, 446:664-667.

[32]Michael J.Barber. Modularity and community detection in bipartite networks. Physical Review E.

(责任编辑陈小明)

作者简介卜振兴(1982—)，男，山东济宁人，博士。研究方向为安全防范技术与工程。

基金项目社会安全基础工作对象信息采集与提取技术研究(2013BAK02B01)。

中图分类号D035.393