Semi-continuous casting of magnesium alloy AZ91 using a filtere melt delivery system

Mainul Hasan*,Latifa Begum

Department of Mining&Materials Engineering,McGill University,M.H.Wong Building,3610 University Street,Montreal,QC H3A 0C5,Canada

Semi-continuous casting of magnesium alloy AZ91 using a filtere melt delivery system

Mainul Hasan*,1,Latifa Begum

Department of Mining&Materials Engineering,McGill University,M.H.Wong Building,3610 University Street,Montreal,QC H3A 0C5,Canada

A 3-D numerical simulation of an industrial-sized slab caster for magnesium alloy AZ91 has been carried out for the steady state operational phase of the caster.The simulated model consists of an open-top melt delivery system fitte with a porous filte near the hot-top.The melt fl w through the porous filte was modeled on the basis of Brinkmann-Forchimier-Extended non-Darcy model for turbulent fl w.An in-house 3-D CFD code was modifie to account for the melt fl w through the porous filte.Results are obtained for four casting speeds namely,40,60,80,and 100 mm/min.The metal-mold contact region as well as the convective heat transfer coefficien at the mold wall were also varied.In addition to the above,the Darcy number for the porous media was also changed.All parametric studies were performed for a fi ed inlet melt superheat of 64°C.The results are presented pictorially in the form of temperature and velocity fields The sump depth,mushy region thickness,solid shell thickness at the exit of the mold and axial temperature profile are also presented and correlated with the casting speed through regression analysis. ©2015 Production and hosting by Elsevier B.V.on behalf of Chongqing University.

Magnesium alloy AZ91;VDC casting;Slab caster;3D CFD modeling;Porous filter Non-Darcy model;Turbulent melt fl w;Solidification Mushy region

1.Introduction

Though at the beginning of the twentieth century the commercial applications of magnesium alloys started,it is only recently that the commercial demand for magnesium alloys has grown to a sizeable amount.The production rate of magnesium and its alloys is still at a minuscule compared to aluminum alloys.It is reported that in 2010,less than 0.7 million tons of magnesium were produced compared to 25 million tons of aluminum[1].The cast products of magnesium alloys are predominantly supplied to the vital industries such as aerospace, automotive,packaging(including beverage cans),construction, etc.Because of its low specifi density,good castability and machinability,high specifi strength and specifi stiffness,good electromagnetic shielding characteristics,etc.[2],the new uses of magnesium alloys are increasing day-by-day.The modern uses of magnesium sheet include cell phone bodies,computer cabinets,inner panels on the doors and trunks of cars and trucks,etc.[3].

The vertical direct chill casting(DCC)is the preferred method which is used universally for casting of large crosssectional slabs and round billets of various aluminum alloys[2]. This method is also used to cast other non-ferrous alloys,such as magnesium alloys,copper alloys,zinc alloys,etc.The casting process in this method starts by feeding the melt through some form of a melt delivery system into an open-ended water-cooled mold.Initially,the bottom end of the mold is kept-plugged by a starter metallic block which is fitte with a hydraulic ram at the bottom.When molten metal comes in contact with the cooled mold walls and the upper-surface of the bottom block,it solidifie and forms an embryonic shell containing liquid metal within the shell.Once a pre-determined height of liquid metal is fille within the mold cavity,the starter block holding the shellliquid assembly is slowly moved downward toward the casting pit with the help of the hydraulic ram.The speed of the starter block is then gradually increased until a constant casting speed is reached.Once the cast is out of the mold,it is further cooled by spraying water coming out from the bottom of the mold onto the outer surface of the embryonic ingot.The cooling that takes place in the mold region is called primary cooling where only10 to 15%of the total heat content of the ingot is removed.The heat extraction from the ingot that takes place below the mold is called secondary cooling where 85%to 90%of the total heat content is extracted.In a typical DCC process,it takes about fi e to ten minutes to reach a quasi-steady state.Depending on the casting speed(which normally varies between 40 and 100 mm/min for magnesium alloys)and the size of the cast, the total operation of this semi-continuous process usually lasts for about 100 to 120 minutes[1].

Nomenclature

D hydraulic diameter of the caster(the entire cross-section of the ingot)

flliquid fraction

fssolid fraction

h sensible heat

h∞ambient enthalpy

H total heat(sensible and latent)

k turbulent kinetic energy

P hydrodynamic pressure

S source term

SΦsource term associated with Φ

T temperature

Tininlet temperature

Tlliquidus temperature

Tssolidus temperature

Tsurfslab surface temperature

uivelocity component in thei-thdirection;

corresponding to u

uininlet velocity

uscasting speed

U,V,W non-dimensional form of the u,v and w velocities

Usnon-dimensional form of us

x axial direction

y horizontal direction parallel to the wide face

z horizontal direction parallel to the narrow face

X,Y,Z non-dimensionalform of x,y,z

i,j,k coordinate direction

Greek symbols

∆Hnodal latent heat

∆Hflatent heat of solidificatio

ΓΦdiffusion coefficien associated withΦ

ρalloy density

µllaminar viscosity

µtturbulent viscosity or eddy diffusivity

Φgeneralized dependent variable

Гeffeffective diffusivity

є rate of energy dissipation

γ effective convective heat transfer coefficien

Superscripts

* non-dimensional variables

Oneofthemajorproblemsofdealingwithmagnesiumalloys is that they are very reactive in the presence of air.As a result, before casting these alloys,there is a need for extreme precaution.The DC casting of these alloys is usually carried out in an open-top,hot-top mold where pressurized inert gas is supplied at the top so that the liquid magnesium alloy is not in contact with the atmospheric air.Usually,a simple ring with outlet holes is used to deliver the cover gas to the melt surface. Another very important precaution is taken while DC casting of these alloys so that the alloy does not come in contact with the coolingwaterinthemold.Anaccidentalcontactwiththecooling waterhasbeenfoundtoleadtoanexplosionandcancreateafatal situation for the personnel in the cast shop.Besides the above points,unlike aluminum alloys the magnesium alloys are delivered from the launder trough assembly through insulated stainlesssteeltubestothehot-topDCcaster.Thelaunder-trough assembly is also usually made of stainless steel.The reason behindthisisthefactthatmoltenmagnesiumreactswithmostof the refractory materials used for aluminum which commonly contain silicates of some form.Because of the aforementioned difficulties extreme precautionary steps need to be critically imposedforthecastingofmagnesiumalloysandareusuallycast inafacilityhavinglessthan10toncapacity.Onthecontrary,the DC casting facility of aluminum alloys is much larger and usually has a capacity of 200–300 tons.For the same output,the production cost for magnesium is much higher than aluminum for the above mentioned necessary safety measures[1].

It is well-known in the DCC industry that various types of inclusions from various sources end-up during feeding of the molten metal into the hot-top mold.Since in a standard DCC facility there is no way to remove these unwanted inclusions after the melt passes the launder-trough,they end up in the cast products and significanty deteriorates the quality of the products.In the present study,a placement of a porous filte within the hot-top and above the mold is proposed.The function of the porous filte is to arrest the inclusions before the melt enters the mold inlet[2].

With the above aim in view,the major objective of our present study is to carry out three dimensional coupled fl w and solidificatio modeling of an industrial-sized slab caster for magnesium alloy AZ91.Although magnesium alloys have a lower thermal conductivity,lower volumetric specifi heat and lower latent heat of solidificatio compared to aluminum alloys, unfortunately because of the long freezing range these alloys initially solidify at a faster rate but the shell thickens inward at a much slower rate due to the large internal thermal gradients. Therefore,to prevent the bleed-out conditions at the exit of the mold,the prediction of shell thickness there is of utmost importance before embarking on the actual design of DCC for magnesium alloys.If a bleed-out condition arises,a catastrophic and fatal situation in the DCC facility will inevitably occur and this is especially true for magnesium alloys.A comprehensive mathematical modeling study can offer some guidelines during the initial phases of the caster’s design such that unwanted bleed-out conditions could be avoided.Except for our earliermodeling study concerning DCC of magnesium alloy AZ31 in a low-head hot-top mold,we are not aware of any comprehensive modeling study of a DCC process concerning the alloy AZ91.Apart from the variations of the thermo-physical properties between AZ31 and AZ91,the present study is concerned with a standard hot-top mold with a porous filte near the hot-top.Because of the placement of the filte,for turbulent melt fl w,the modeling complexity has increased quite signifi cantly.Since a relevant study is not available in the published literature,hence we do not feel that there is a need here to discuss the general literature concerning DCC of magnesium alloys.Interested readers can consult a recent book concerning the DCC casting of aluminum and magnesium alloys to follow the time-wise improvements of the DCC process[1].

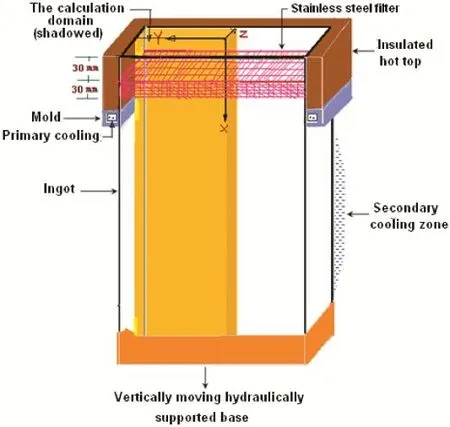
Fig.1.Schematic of a vertical DC caster with the calculation domain represented by yellow color.

2.Mathematical model

The physical model and the computational domain(yellow color region)considered in this study is schematically shown in Fig.1.In order to decrease the computational time,the present two-fold symmetry problem has been exploited and only a quarter of the physical domain was considered for the simulations.The dimensions of the simulated domain of a typical industrial scale slab DCC are listed in Table 1.The coordinates of the computational domain are selected at the center of the caster at the top surface.Melt is delivered at the top free-surface with a uniform velocity across the entire cross-section of the caster.At a vertical distance of 30-mm from the top freesurface,a porous filte is occupying the total horizontal crosssection of the caster.It is expected that the porous filte will arrest the inclusions in the melt and will allow the melt to fl w through the filte which will reduce significanty the momentum of the incoming melt and will distribute the melt homogeneously to the mold underneath.The porous filte is assumed to be made of stainless steel so that it can withstand the heat and the impact of the incoming melt.The thermo-physical properties of the material of the porous filte are given in Table 2.2.1.Test material

As stated earlier,the common magnesium alloy AZ91 was selected to predict the solidificatio behavior of this alloy in avertical DCC process for a slab.The chemical composition limits of this alloy are listed in Table 3[4]and its thermophysical properties are summarized in Table 4[4].AZ91 alloy is a magnesium alloy to which some 9%of aluminum and 1% of zinc are added in order to improve its corrosion resistance. Other minor alloying elements in this alloy are manganese, silicon,copper,etc.Magnesium is abundantly available in nature and it is an environmentally-friendly metal because of higher energy efficien y and recyclable properties.Sheets of AZ91 alloy are used in the housing of mobile phones and laptop computers as well as the cored bar on wheels and other automotive components.

Table 1Geometrical parameters for the caster and porous plate.

Table 2Physical properties of stainless steel for the porous plate.

2.2.Assumptions and simplification

The following realistic assumptions were invoked in order to simplify the modeling effort and computational time of the present complex industrial slab DCC of magnesium alloy AZ91:

1 In the simulation,a fi ed-coordinate system(Eulerian approach)was employed.

2 Local thermodynamic equilibrium during solidificatio was assumed to prevail.Heat fl w was taken to be very fast and every point reached equilibrium with its neighboring points instantaneously.

3 A mushy-fluisolidificatio model was assumed and pore formation was ignored.

4 Flow in the mushy region was modeled similar to a fl w through a porous medium.

5 Molten magnesium alloy was assumed to behave as an incompressible Newtonian fluid

6 Any heat released due to solid-solid transformation was not taken into consideration.The formation of intermetallic compounds during solidification was ignored.

7 Evolution of latent heat in the solidificatio domain was not influence by the microscopic species transport,that is,the liquidus and solidus temperatures were fi ed.

8 Because of the lack of experimental results,the variation of the liquid fraction in the mushy zone was assumed to be a linear function of temperature.

9 The thermo-physical properties of magnesium were invariant with respect to the temperature and there was no viscous dissipation effect.The thermal buoyancy effectwas incorporated in the momentum equations by employing the Boussinesq approximation.

Table 4Thermo-physical properties of AZ91.

10 Only the steady-state phase of the caster’s operation was modeled without taking into account the transient start-up condition.

11 The porous filte was considered as non-deformable, homogeneous and isotropic porous media,which was saturated with the incoming melt.

12 The solid matrix of the porous media of the filte was considered to be in local thermal equilibrium with the surrounding melt.

2.3.Numerical formulation

2.3.1.Governing equations for laminar melt velocity and enthalpy

The 3-D general governing transport equations for laminar/ turbulent melt velocity and enthalpy at steady state using the tensor notations in the Cartesian coordinate system can be written as follows:

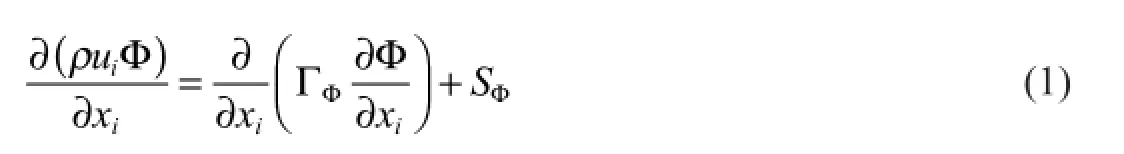
where ρ is the melt density anduiis the velocity component in thexi–direction and Φ can be the dependent variable such as 1 for continuity equation,velocityui,temperature T,ΓΦis the effective diffusion coefficien of Φ and SΦis the source term of Φ.The gravity force is acting in the positive x-direction.

Although the present problem is a multi-phase problem,but for the sake of convenience in solving this problem,a single domain approach was followed in the present simulation since it does not require the tracking of the unknown interfaces (liquid-mushy and mushy-solid).In the present work,the wellknown enthalpy-porosity based method was implemented [5–8].The Darcy law for porous media was used to predict the fl w of the molten metal in the mushy region[7,8].

2.3.2.Non-dimensionalization of the governing equations and boundary conditions

For the clear flui region,the 3-D turbulent Navier–Stokes and energy equations were used and the low-Reynolds numberversion of the popular k-εeddy viscosity concept proposed by Launder and Sharma[9]was adopted to account for the turbulence levels in the liquid pool.Since from the dimensional equations it is not possible to ascertain the parameters which govern the process,hence the equations and boundary conditions were non-dimensioned in order to obtain the relevant parameters and for the generalization of the results.The following dimensionless variables were used to non-dimensionalize the governing partial differential equations and boundary conditions for the melt region:

Table 3Chemical composition limits of AZ91.

Table 5Summary of the non-dimensional governing equations for the melt region.

where D is the hydraulic diameter of the open-top cross-section (which is equal to the total cross-section of the caster),uinis the inlet velocity at the open-top and∆Hfis the latent heat of solidification All the conservation equations can be expressed in a general form of a non-dimensional partial differential equation.The Cartesian-tensor form of this equation is:

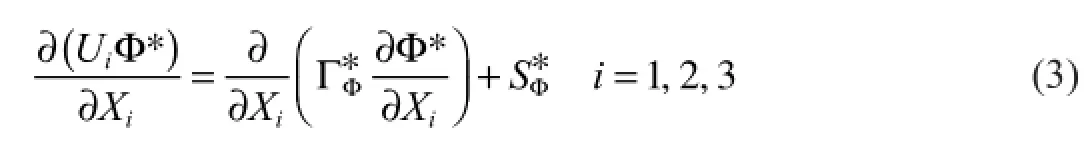
Open inlet

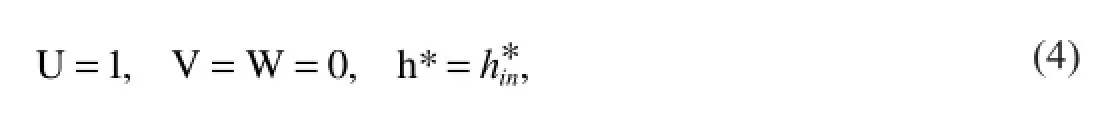
Symmetry planes

Outlet

Moving walls

where γ is the effective heat transfer coefficien between the solid surface and the surrounding,represents the nondimensional enthalpy at the ingot surface andrepresents the non-dimensional ambient enthalpy.The values of the effectiveheat transfer coefficien along the length of the slab were taken from Vreeman and Incropera[10],which are given below:

where x1=210 mm,x2=220,x3=260 mm and γgap=0.15 kW/(m2-K),γmax=20.0 kW/(m2-K),γfli=10.0 kW/(m2-K).

A point to note here is that in the present model,the non-dimensioned transport equations and associated boundary conditions were solved,which therefore generated nondimensional results.To make the results easily understandable to the readers,all predicted results in this paper are reported and discussed in their primitive(dimensional)forms.

2.3.3.Modeling of porous filte

As mentioned earlier,a 30-mm thick stainless steel filte was placed at a vertical distance of 30-mm from the top free surface across the entire cross-section inside the hot-top.The main purpose of the present study was to investigate the influenc of the porous filte on the melt fl w behavior,temperature distributions,and solidificatio characteristics in the mold and post mold regions of a DC caster.

To model the DC casting process with an internally placed filte,two different sets of transport equations(continuity, momentum and energy)for clear flui and porous regions are needed.For clear flui region,the time-averaged turbulent form of the governing conservation equations are well known.For the mathematical description of the laminar fl w in the porous media,the extended form of the Brinkman-Forchheimer-Darcy model is used.In Cartesian-tensor notation,the transport equations for the porous filte are as follows[11–14]:

Momentum equation:

where K=permeability ofthe porousmedia;φis the porosity (void fraction) of the porous matrix;CF=Forchheimer coefficient .Following Vafai et al.[15],can be represented as:the value 0.55 ofCFwas used in this work.keffective=effective thermal conductivity =φkfluid+(1 −φ)ksollidin the energy equation.It is to be noted here that the nondimensional transport equations for the porous filte contained two additional parameters,porosity (φ)of the medium and Darcy number(Da=KD2),both of which needed to be prescribed before solving the equations.

2.3.4.Solution procedure

To discretize the equations,a control volume(CV)based finit difference approach was adopted.Four staggered control volumes,three non-overlapping control volumes for the three components of velocity and one control volume for the scalar variables were employed in the computational domain.A hybrid difference scheme[16,17]was used to discretize the convection-diffusion terms.In the present study there are seven variables,namely,U,V,W,P*,k*,ε*,h*which were solved sequentially to obtain a converged solution.To resolve the velocity-pressure coupling in the three momentum equations, the SIMPLE algorithm[16,17]was used.The discretized equations for each variable was declared to have converged when the sum of the residuals for that particular variable(RΦ)was less than 0.001.The convergence criterion described above can be define mathematically as follows:

The CPU time per iteration was about 1.0 min.The computations were performed on a personal computer having a speed of 2.66 GHz and fitte with a RAM of 4 Gigabytes.In a typical case,to obtain a fully converged solution,it took about 3.5 days and required more than 5000 iterations.

Before carrying out extensive parametric studies,the grid independency tests were firs performed using three sets of successively refine meshes(coarse,moderate,and fine)The relative difference in the local surface heat flu between the coarse and fin grids was within 1.0%,indicating that the coarse grid was sufficien for predicting the results of engineering accuracy.It is to be stressed here that the local surface heat flu is the most sensitive quantity with regard to grid in any heat transfer problem.A comparison(see ref.7)of the surface temperature profile showed less than 0.2%variation between the fin and course grid systems.Therefore,the coarse grid (60×42×24)was used for all production runs reported in this work.The details of the predicted results along with the comparisons can be found in reference 7.

A code validation test was also carried out by simulating the solidificatio of a rolling ingot forAA-3104 alloy,using theidentical experimental casting conditions and set-up for the vertical DCC process performed by Jones et al.[18].The present in-house developed code showed an acceptable agreement with the experimental data.These results were presented in reference 7 and are not given here to avoid duplication.

Table 6Values of the parameter used in open-top melt delivery arrangement.

3.Results and discussion

In the present study,the four important parameters,namely, casting speed,HTC at the metal-mold contact region,metalmold contact length,and Darcy number of the porous filte were varied,all for a fi ed melt inlet superheat of 64°C and for a porosity of the filte of 0.4.For the aforementioned parameters, a large number of results were generated.From these results, only selected results are presented here to clarify the solidifi cation characteristics of the casting process.The change of the above parameters has resulted in fourteen distinct parametric cases which are listed in Table 6.The inlet Reynolds and Peclet numbers for each case are also shown in Table 6.

3.1.Velocity and temperature field for cases(1–4)of Table 6

The 3-D surface plots of the predicted velocity and temperature field for the firs four cases(1–4)of Table 6 are presented in Figs.2(i-iv).The calculation domain in each figur shows two symmetry planes[wide(x-y plane)and narrow(x-z plane)] as well as the melt entry surface of the ingot.Fig.2b,d,f,h shows the corresponding velocity vector field in the corresponding planar surfaces.

The velocity vector plots show that all of the melt fl ws downward along the casting direction.The reason for this fl w pattern is the fact that the melt in this feeding scheme is supplied at a constant inlet velocity at the top of the hot-top region along the entire top cross-section of the caster.As the melt reaches from the clear flui region into the porous filte below, it is being directed downward by the open pores of the filte.The momentum of the downward fl w inside the filte is signifi cantly reduced due to the hydraulic resistance of the porous media.At the exit of the filte,the momentum forces direct the fl w downward.At the narrow and wide sides,the melt is bent and fl ws downward and towards the center in an inclined way. This is due to the fact that as the melt contacts the solid shell that forms along the narrow and wide faces,it is redirected along the solidificatio front.

In general,an increase in the casting speed results in an increased rate of the mass of the melt entering the caster,which is accompanied by a relatively large amount of heat content.A comparison of Fig.2b,d,f,h clearly shows that in the liquid pool, the magnitudes of the velocity increase with the increase of the casting speed.

The surface temperature distributions in floode format are presented in Fig.2a,c,e,g for the range of casting speed of 40–100 mm/min representing cases(1–4)of Table 6.These numerically predicted temperature data clearly show the progressionofthesolidificatio processfortheabovementioned cases.The solidificatio range of magnesium alloy AZ91 is 125°C which is an intermediate freezing range alloy.The present results indicate that the mushy region,which is bounded by the liquidus(595°C)and solidus(470°C)isotherms,is expanded as the casting speed is increased due to the strong thermalconvectiveeffects.Furthermore,aclassicallyparabolicshaped solidificatio front is seen to have been developed particularly if one looks from the central axis at each casting speed.The melt near the wall loses superheat and as a result the effect of thermal convection reduces compared to thermal conduction effect as the melt moves from the wall region to the centralregion.Theparabolicshapeofthesolidificatio profil is the manifestation of the above fact.As the casting speed increases,the solidificatio front as well as the other isotherms are becoming steeper and are moving downward,which has already been found by several other authors[1,2,19].

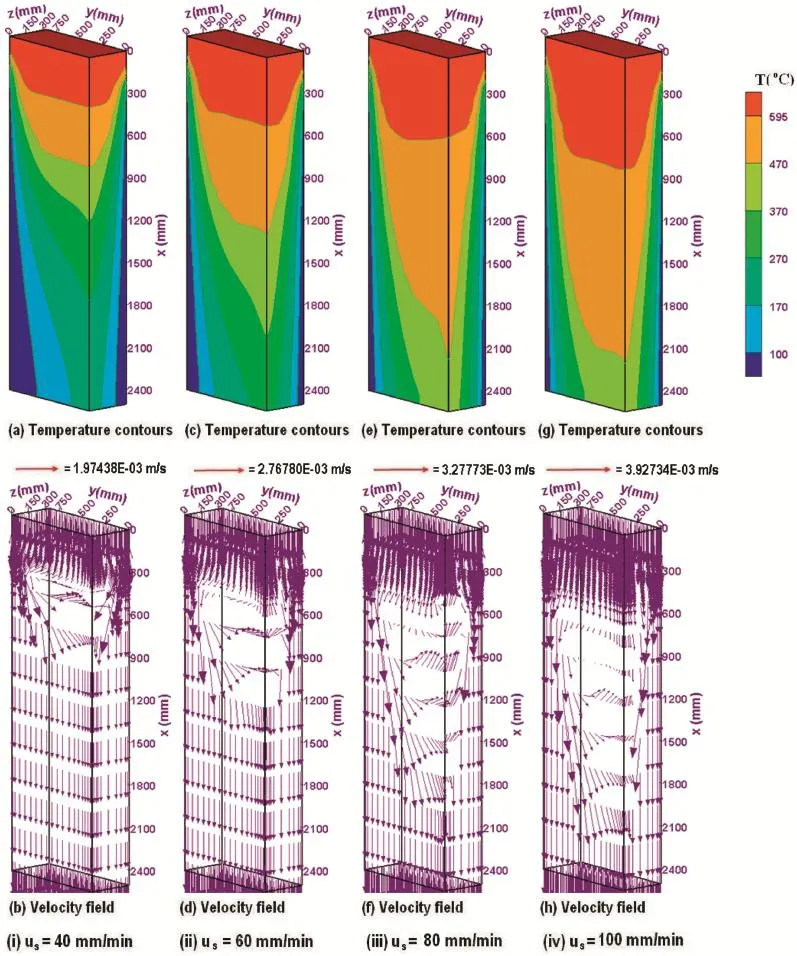
Fig.2.3-D surface plots of temperature and velocity field for four cases(1–4).

Fig.3.Longitudinal 2-D views of temperature contours and velocity vectors for case 1.

Figs.3a–c–6a–c illustrate explicitly a 2-D temperaturecontours and vector fielat the wide symmetry plane(z=0) and parallel to the wide symmetry plane at z=62.5 mm,and z=312.5 mm for the four cases(1–4).The left hand panels of these figure show the temperature contours while the right hand panels depict the velocity vectors at these three longitudinal cross-sections.The right hand panels of Figs.3a through 6a show the velocity vectors in wide symmetry plane(z=0)forfour casting speeds.The velocity vector plot of each of these figure illustrates the strong vertical stream of hot melt is coming from the top of the domain.The corner stream is impacting onto the solid front near the narrow face and is diverted and it moves along the solidificatio front,while the rest of the stream in the other part of the ingot is fl wing vertically downward,as seen in these figures The velocity field in the right hand panels,at z=62.5 mm and z=312.5 mm,for four cases(1–4)are presented in Figs.3b through 6b,and 3c through 6c,respectively.A close look at the velocity vector fiel in each panel at z=62.5 mm shows the corner stream near the narrow face is still obstructed by the developing solidificatio front,whereas the velocity fiel at z=312.5 mm,which is close to the rolling face,shows a uniform downward fl w.The magnitude of the velocity vectors at z=312.5 mm is almost equal to the casting speed.

The temperature contours in the left-hand panels,at z=0, z=62.5 mm and z=312.5 mm,for four cases(1–4)are presented in Figs.3a through 6a,3b through 6b,and 3c through 6c, respectively.As one moves toward the rolling face from the slab center,the heat extraction rate increases,which is reflecte in the shapes and locations of the isotherms at these three longitudinal cross-sections and the isotherms are seen to have lifted upward.These figure further show that with the increase of the casting speed,both liquidus and solidus isotherms are shifted downward and the vertical distance between them is increasing.

Among the various possible options to represent the solidificatio heat transfer phenomena,the 2-D transverse crosssectional planes(y-z plane)are chosen to get a vivid picture of the solidificatio process happening within the ingot.The liquidus and solidus isotherms are plotted in Fig.7a–d for four cases(1–4).A total of seven transverse cross-sections starting from just above the mold and up to an axial distance of 700 mm have been selected.The numerical results show that a nearly uniform thick solid shell on the narrow and wide faces is formed and as one moves downward the extent of the solid shell increases progressively.Since more heat is being extracted from the ingot through the mold and by the chilled water jets,both of the latter factors are contributing in increasing the thickness of the solid-shell along the cast direction.It appears from the progression of the solid-shell thickness that an almost uniform rate of heat extraction is taking place from both the sides.At the corner region,heat is being extracted from both the rolling and narrow faces;this has resulted in a higher rate of heat extraction at that location compared to the other places.As a result,an almost round-shaped solid layer and mushy zone have formed there.The location of the solidus isotherm with the decrease in the casting speeds has shifted more toward the ingot center over each cross-section compared to the higher casting speed,which can be clearly seen in the above figures The primary reason in the reduction of heat transfer with increasing casting speed is that for a higher casting speed,the amount of incoming melt as well as the energy content of the melt are both higher.

3.2.Sump depth and mushy layer thickness

During the DCC process,the objective of an operator is to keep the sump depth low and the mushy layer thinner.A higher sump depth and thicker mushy layer have been found to yield relatively poor quality casts.Since the latter two quantities,in addition to the alloy being cast,also depend on the number of processing variables as well on their interaction effects,hence the mentioned variables cannot be rationally controlled.During the experimental campaign,the sump depth and mushy thickness are also quite difficul to measure accurately.In the modeling of the process,these two quantities are not the direct outcome of the predicted results.In the present modeling study, the latter two quantities were obtained by post processing the predicted temperature field from the CFD model.Table 7 provides the quantitative values of the sump depth and mushy thickness at the center of the ingot for four casting speeds representing cases(1–4)of Table 6.The present authors are surprised by the fact that in none of the vast literature on DCC process has reported the quantitative values of the sump depth and mushy thickness against the casting speed for any nonferrous alloy for a slab caster.Table 7 clearly shows that with the increase of the casting speed,the sump depth and mushy thickness are increasing.In order to compare the relative differences in sump depth and mushy thickness,the lowest simulated casting speed of 40mmmin is considered as the reference case.The sump depth for this case is found to be approximately 655.6 mm from the top of the mold.The relative difference in sump depth for higher casting speeds of 60,80, and100mmmin is respectively about 72.0%,205.4%,209.9% higher.For the casting speed of40mmmin ,the mushy thickness is found to be 428.8 mm,whereas for casting speeds of 60mmmin,80mmmin,and 100mmmin ,the mushy thickness increases by 78.5%,148.2%,and 220.0%,respectively compared to the casting speed of40mmmin.

3.3.Predicted shell thickness

Among the casting parameters the casting speed is one of the influentia factors which dictate the growth rate of the solid shell.To understand the solidificatio phenomena clearly,one critical location at the exit of the mold on the slab surface has been selected.The location is on the narrow side at the wide symmetry plane.The quantitative results of shell thickness are plotted in the form of a bar chart in Fig.8 in order to get a comparative picture of the differences among the results for four cases(1–4).The numerical value of the predicted shell thickness(in mm)is provided inside each bar of the chart of Fig.8.With the increase of the casting speed the shell thickness decreases,which is consistent with the physical nature of this casting problem.

3.4.Predicted strand surface temperature

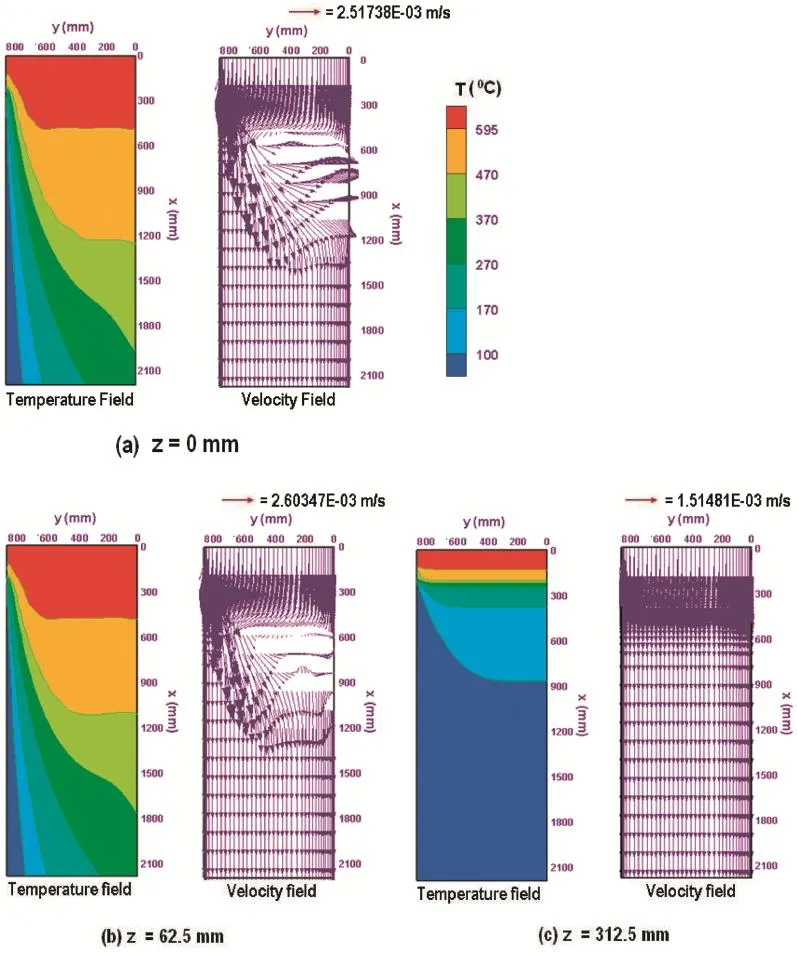
Fig.4.Longitudinal 2-D views of temperature contours and velocity vectors for case 2.

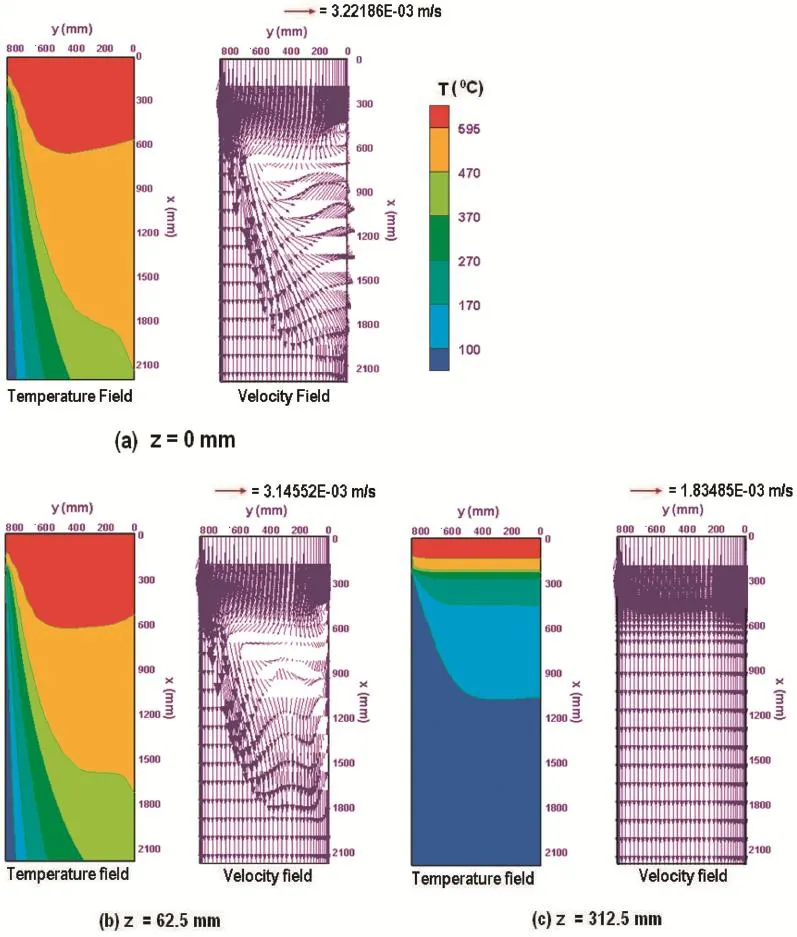
Fig.5.Longitudinal 2-D views of temperature contours and velocity vectors for case 3.

Fig.6.Longitudinal 2-D views of temperature contours and velocity vectors for case 4.

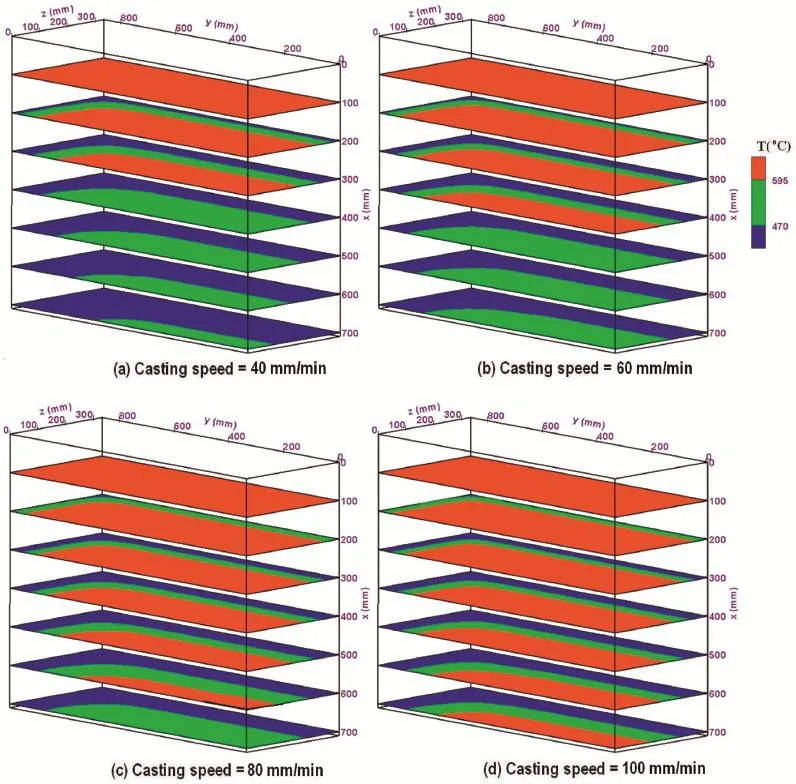
Fig.7.Contours of solidus and liquidus temperatures at various transverse cross-sectional planes for four cases(1–4).

Table 7Sump depth and mushy thickness in mm at the ingot center for cases(1–4).

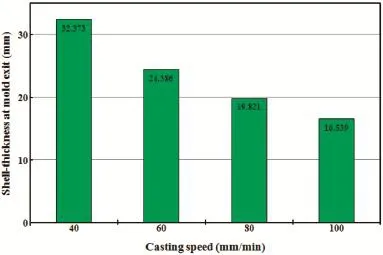
Fig.8.Shell thickness at the middle of the narrow slab face at mold exit vs. casting speed for cases(1–4).

Fig.9a and b illustrates the temperature distributions along the caster for two cases(2 and 4)which correspond to the casting speed of 60 and 100mmmin ,respectively.Since the convective boundary conditions were imposed on the strand surfaces,as a result the surface temperatures were not known there in advance.To get the strand surface temperature at any grid point,a heat balance on the control volume corresponding to that grid point was done after getting the converged solution of the problem.To demonstrate the temperatures on the cast surfaces,a total of four strategic locations are selected in this study,namely:(a)center;(b)mid-distance of the wide face;(c) mid-distance of the narrow face;and(d)corner point of the caster.These are the locations which are believed to be the most sensitive zones for the initiation of different types of crack,such as edge crack,surface crack,mid-crack,etc.The four locations are portrayed on the top of Fig.9a and b for easy reference. Except for the temperature at the ingot central region,the temperatures are seen to follow the same pattern at three other locations.For cases 2 and 4 of Table 6,the metal-mold contact region was prescribed as 30 mm and the air-gap region as 50 mm,both together constitute a total mold length of 80 mm. One should recall here that a hot-top of 130 mm in length is above the mold where the outside walls were assumed to be thermally insulated.In the mold-metal contact region,the temperature of the solid shell decreases rapidly because of the implementation of a convective cooling condition with an HTC of 2000 W/(m2-K).After the metal-mold contact region,initially at the air-gap region the temperature of the solid shell rebounded.This is due to the implementation of a low HTC of 150 W/(m2-K)there.The latter value of HTC is imposed in the air-gap region to reflec the reality of an actual condition within the mold region of a caster.Subsequent to the increase in temperature in the rebound region,the temperature of the surface of the solid shell drops quite sharply due to the imposition of an intense cooling condition in the impingement water jet region near the mold exit.It is to be realized here that the impingement cooling renders significan cooling effects in the upstream into the air-gap region within the mold.After the impingement cooling,the surface of the solid shell is seen to cool rather slowly in the secondary cooling region.Although the HTC at the secondary cooling region is high(10 000W/(m2-K)),due to the internal thermal resistance of the growing shell, the cooling rate of the solid shell decreases drastically in this region which is reflecte by the lower temperature gradient there.At the central region,initially the temperature drop is rather low because of the incoming hot melt.In the secondary cooling region,there is a significan temperature drop due to the fact that a large amount of superheat is lost in the mold region for that location.A comparison of the two figure clearly shows that for a higher casting speed,the surface remains overheated for the same axial location compared to the lower casting speed. This trend is visible in all of the four ingot locations.The reason behind this is the fact that the predictions were carried out for the lower and higher casting speeds by invoking the same convective heat transfer boundary conditions without considering the enhanced cooling requirements for a higher casting speed.

3.5.Effect of heat transfer coefficien at the metal-mold contact region

Among the researchers working in this fiel,there are serious disagreements regarding the values of the effective heat transfer coefficient in the metal-mold contact region.From the literature one gets conflictin values of the HTCs in the metalmold contact region.Even the well refereed literature on this issue has reported a wide range of values for the HTCs.In the metal-mold contact region,a value of HTC ranging from 1000 to 5000 W/(m2-K)has been reported in the well-cited literature [1,20].In order to ascertain the impact of the heat transfer coefficien(HTC)at the mold-metal contact region,for an inlet superheat of 64°C,three HTC values of 1000,2000 and 4000 W/(m2-K)were selected for the two casting speeds namely, 60mmminand 100mmmin .Fig.10 reports the values of the shell thickness against the HTCs in the form of a bar chart for the above mentioned two casting speeds.

The shell thickness is estimated from the temperature profile at the mold exit at an axial distance of 90 mm from the top surface on the wide symmetry plane from the narrow face.It can be seen that for an increase of HTC,the magnitude of the shell thickness increases.Similar trends are found for both casting speeds.For a fi ed HTC,the shell thickness decreases with casting speed as noticed earlier.For a lower casting speed of 60 mm/min,an increase of the HTC from 1000 to 2000 W/(m2-K)has caused an enhancement of 16.64%in solid-shell thickness and for the increase of HTC from 2000 to 4000 W/(m2-K)the increment is almost the same and is approximately 14.84%.For a higher casting speed of 100 mm/min, the corresponding increase in the shell thickness is about 39.66%and 24.59%,respectively.Hence,it is clear that the effect of lower HTCs(from 1000 to 2000 W/(m2-K)) on shell thickness is more pronounced at a higher casting speed.

3.6.The effect of metal-mold contact length

Fig.11 portrays in the form of a bar chart the shell thickness (in mm)at the middle of the narrow face at the mold exit against prescribed metal-mold contact length of 20,30 and 50 mm for the casting speeds of 60 and 100 mm/min and all for a fi ed HTC of 2000 W/(m2-K).It should be mentioned here that almost all researchers working in this fiel agree that the molten metal due to the thermal shrinkage during solidificatio does not remain in contact with the mold for the total length of the mold and an air-gap develops in the lower part of the mold which separates the embryonic solid shell from the mold wall. Unfortunately,regarding the extent of the metal-mold contact region(lower air-gap region in effect)in the upper part of the mold,the consensus is not there among these researchers[20]. The above figur shows that with the increase of metal-mold contact length,the solid shell thickness increases for both casting speeds.This is expected since for a larger metal-mold contact length,more heat is being extracted from the hot incoming melt through the mold walls.Since the mold is 80 mm in length,with the increase of the metal-mold contact length there is a corresponding decrease in the length of the air-gap region.The low rate of heat extraction in the smaller air-gap region thus indirectly contributes in the enhancement of the shell thickness.

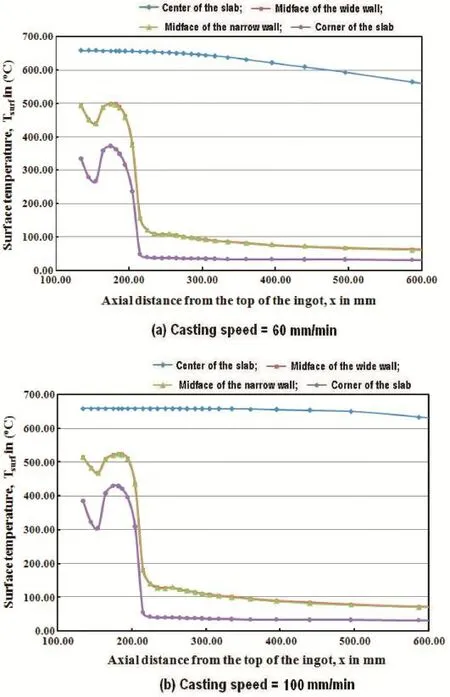
Fig.9.Variations of surface temperature along the axial direction of the strand at four locations of the caster for:(a)us= 60mmmin−1(case-2)(b)us= 100mmmin−1(case-4).

This figurfurther shows that for the change of contact length from 20 to 30 mm for the higher casting speed(100 mm/ min),the rate of increase of the shell thickness is much higher compared to the lower casting speed(60 mm/min);the rate of increase is 33.9%versus 7.7%,respectively..For the increase in the contact length from 30 to 50 mm,for the lower casting speed of 60 mm/min,the rate of increase is lower(14.8%);and for the higher casting speed of 100 mm/min,the rate of increase is also much lower(20.9%).

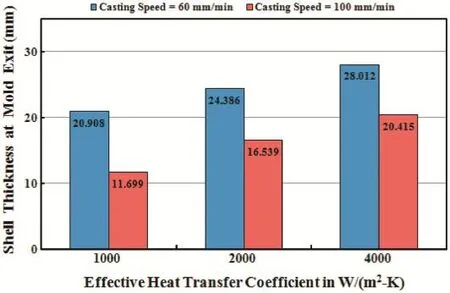
Fig.10.Shell thickness at the middle of the narrow face at mold exit vs.effective HTC(W/(m2-K))for six cases(2,4,and 5–8).

3.7.The effect of Darcy number of the porous filte

In order to study the effect of permeability(Darcy number) of the porous filte,simulations are carried out with the two-fold decrease of the Darcy number from the standard base case of 10−4(cases 13 and 14 of Table 6).Fig.12 shows the effect of shell thickness at the middle of the narrow face at the exit of the mold for a constant metal-mold contact length of 30 mm,HTC of 2000 W/(m2-K)and for two casting speeds of 60 and 100 mm/min.The figur clearly shows that for the two order of magnitude change of the Darcy number,there is no significan effect on shell thickness.This outcome is expected since the porous filte is placed in the hot-top region above the mold to arrest the incoming inclusions in the melt before it enters the mold;as a result,the thermal fiel is not much affected within the mold by the presence of the filte.It should be noted here that the actual mechanism how the inclusions are arrested by the porous filte has not been included in the analysis since such a study is very challenging and will require a completely separate study.

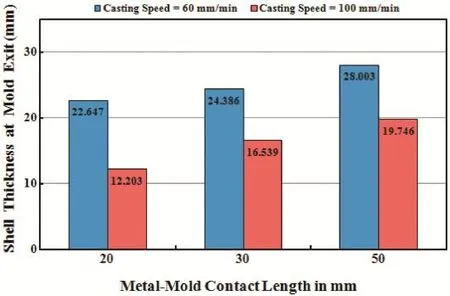
Fig.11.Shell thickness at the middle of the narrow face at mold exit vs.metal-mold contact length(mm)for six cases(2,4,and 9–12).

Fig.12.Shell thickness at the middle of the narrow face at mold exit vs.Darcy number for four cases(2,4,and 13–14).

4.Conclusions

During this investigation,the effects of the casting speed, metal-mold contact length,effective heat transfer coefficien at the metal-mold contact region and Darcy number(permeability)of the porous filte have been studied.From the 3-D turbulent CFD modeling study of a conventional hot-top,vertical DC slab casting processes for the magnesium alloy AZ91,the following conclusions are drawn:

1 For an inlet superheat of 64°C,for the range of casting speeds varying from 40 to 100 mm/min,for the metal-mold contact region variation of 20 to 50 mm with the effective heat transfer coefficien(HTC)at the metal-mold contact region ranging between 2000 W/(m2-K)to 4000 W/(m2-K), the sump depth and the mushy thickness at the center of the ingot do remain confine within the simulated axial length of 2500-mm for all casting speeds.For a lower HTC of 1000 W/(m2-K)and a higher casting speed of 100 mm/min,the sump depth and the mushy region are not confine within the 2500-mm length of the caster.

2 At the center of the caster,a lower depth of the melt pool and a shallower sump are found for the lower casting speeds compared to the higher casting speeds.For the standard cases of 1 to 4 of Table 6,through regression analysis,the sump depth(SD in mm)and the melt pool depth(MP in mm) are found to be linearly related to the casting speed(usin mm/min)by the following equations,respectively: SD=−296.85+25.01us(R2=0.908)and MP=−59.20+ 6.85 us(R2=0.956).

3 The mushy region is bounded by the liquidus and solidus

temperatures of the alloy.The vertical distance of the mushy region at the ingot center increases with the increase of the casting speed.For the simulated cases of 1 to 4 of Table 6, the mushy thickness(MT in mm)can be represented by the following linear equation with regard to the casting speed(usin mm/min):MT=−187.33+15.64us(R2=0.999)

4 To prevent break-out,the solid shell thickness at the exit of the mold is a very important quantity for the operators of the casters.The results show that it decreases with the increase in the casting speed in a linear fashion and the surface temperatures of the strand increase with the casting speed. At the mid-point of the narrow wall at the exit of the mold, the solid shell thickness can be represented by the following linear equation with regard to the casting speed(usin mm/min):ST=41.66−0.26 us(R2=0.963)

5 For a constant cooling water temperature in the mold,with a higher imposed HTC at the metal-mold contact region,the shell thickness at the mold exit is greater.The enhancement of the shell thickness is more pronounced for the lower HTCs at higher casting speeds compared to the lower casting speeds.

6 For a fi ed HTC at the metal-mold contact region and for a constant casting speed,with the increase of the metal-mold contact region the shell thickness increases at the mold exit. The enhancement of the shell thickness is more pronounced for the higher casting speed compared to the lower casting speed.

7 Provided all other parameters are the same,with the two-fold increase in the Darcy number(permeability of the porous filter no significan change in the solid shell thickness at the exit of the mold is found.

Acknowledgment

This work is partially supported from the National Sciences and Engineering Research Council(NSERC)of Canada Discovery Grant RGPIN48158 awarded to M.Hasan of McGill University,Montreal,for which the authors are grateful.

[1]J.F.Grandfield D.G.Eskin,I.Bainbridge,Direct-Chill Casting of Light Alloys:Science andTechnology,JohnWiley and Sons,Inc.,Hoboken,NJ, 2013,p.242,p.334.

[2]H.Hao,Casting Technology and Quality Improvement of Magnesium Alloys,Special issue of magnesium alloys.＜www.intechopen.com/ download/pdf/18847＞,Sep 12,2011,pp.1–24.

[3]Y.B.Zao,B.Jiang,Y.Zhang,Z.Fan,IOP Conf.Ser.Mater.Sci.Eng.27 (2012)Paper No.012043.

[4]＜http://asm.matweb.com＞; and ＜www.aircraftmaterials.com/data/ magnesium/AZ91/html＞.

[5]V.R.Voller,C.A.Prakash,Int.J.Heat Mass Transf.30(1987)1709.

[6]S.H.Seyedein,M.Hasan,Int.J.Heat Mass Transf.40(1997)4405.

[7]L.Begum,3-D Transport Phenomena in Vertical Direct Chill Casting Processes(Ph.D.thesis),Dept.of Mining and Materials Engineering, McGill University,Montreal,Quebec,Canada,2013.

[8]L.Begum,M.Hasan,Int.J.Heat Mass Transf.73(2014)42.

[9]B.E.Launder,B.I.Sharma,Lett.Heat Mass Transf.1(1974)131.

[10]C.J.Vreeman,F.P.Incropera,Int.J.Heat Mass Transf.43(2000)687.

[11]M.H.J.Pedras,M.J.S.de Lemos,Int.Commun.Heat Mass Transf.27(2) (2000)211.

[12]M.H.J.Pedras,M.J.S.de Lemos,Int.J.Heat Mass Transf.44(2001a) 1081.

[13]M.H.J.Pedras,M.J.S.de Lemos,Numer.HeatTransfer PartA 39(2001b) 35.

[14]M.H.J.Pedras,M.J.S.de Lemos,Numer.Heat Transfer Part A 43(2003) 585.

[15]K.Vafai,R.L.Alkire,C.L.Tien,J.Heat Transf.Trans.ASME 107(3) (1985)642.

[16]S.V.Patankar,Numerical Heat Transfer and Fluid Flow,Hemisphere Publishing Corporation,New York,1980.

[17]H.K.Versteeg,W.Malalasekera,An Introduction to Computational Fluid Dynamics,The Finite Volume Method,firs ed.,Pearson/Prentice Hall, Harlow,2007.

[18]W.K.Jones Jr.,D.Xu,J.W.Evans,W.E.Williams,D.P.Cook,Light Met. (1999)841–845.

[19]D.G.Eskin,Physical Metallurgy of Direct Chill Casting of Aluminum Alloys,Advances in Metallic Alloys,CRC Press,Taylor&Francis Group, Boca Raton,FL,2008,pp.120–122.

[20]E.J.F.R.Caron,M.A.Wells,Metall.Mater.Trans.B 40B(2009) 585.

Received 1 October 2015;revised 16 November 2015;accepted 17 November 2015 Available online 8 December 2015

*Corresponding author.Department of Mining&Materials Engineering, McGill University,M.H.Wong Building,3610 University Street,Montreal,QC H3A 0C5,Canada.Tel.:+1 514 398 2524;fax:+1 514 398 4492.

E-mail address:Mainul.hasan@mcgill.ca(M.Hasan).

1ASME Member(#1964840).

http://dx.doi.org/10.1016/j.jma.2015.11.005

2213-9567/©2015 Production and hosting by Elsevier B.V.on behalf of Chongqing University.