基于模型修正的桥梁极限承载力分析

宋 智，孙 强

(辽宁省水利水电勘测设计院, 辽宁 沈阳 110006)

基于模型修正的桥梁极限承载力分析

宋 智，孙 强

(辽宁省水利水电勘测设计院, 辽宁 沈阳 110006)

针对大型预应力钢筋混凝土桥梁极限承载力问题,以辽阳市太子河中华大桥为背景，提出了基于模型修正理论的有限元数值模拟方法。大型钢筋混凝土结构桥梁,具有大跨度、多自由度、多单元、非线性等多重复杂特性,有限元软件建立的初始模型往往存在局限性。为使所建模型能够准确反映实体结构特性,在有限元模型修正理论的基础上,建立了综合考虑多因素的模型,对桥梁结构敏感细节进行了修正。对其进行了极限承载力分析计算。该成果对同类桥梁工程结构的承载力分析具有一定的参考价值和指导意义。

太子河中华大桥；模型修正；有限元模拟；极限承载力

目前,研究钢筋混凝土桥梁(包括预制型、预应力型、现浇等钢筋混凝土桥)的方法主要有以下思路:首先,利用各种计算机编程语言,以非线性有限元为理论基础,编制针对某种特定结构形式桥梁有限元程序,此种方法多用于计算较少单元的简单结构,编制过程困难且计算复杂,有一定的局限性;其次,基于优化理论的模型修正理论分析方法，此种方法具有计算操作过程相对简单,通用性强的优点。

本文基于有限元分析目标的多重因素的模型修正理论,采用修正后的参数,利用ANSYS大型有限元软件,建立能准确反映实体结构的有限元模型,并在此基础上,对太子河中华大桥进行极限承载力的计算研究,保证分析的合理性和结果的准确性。

1 有限元模型修正理论分析

1.1 模型修正阐述

以辽阳市太子河中华大桥的极限承载力分析为目标,用模型修正理论[1-2]避免有限元结构模型预测机制与实际结构响应之间的偏差,以此更加精确的反映结构特性。本文基于设计参数法,对各个反映结构特性有限元模型的敏感参数进行修正。但模型设计参数具有非一致性、非同属性,如材料的弹性模量、密度、几何尺寸,都是属于量化参数;还有一些非量化参数,也会对模量精度产生重要影响,如结构细部敏感要素——是否考虑预应力、锚固大小、焊接应力集中等。对于非量化参数要对其进行修正处理,然后再对有限元参数修正,这样就使设计参数更加完备。

本文采用Bayesian的模型修正法,同时又考虑了非同属性细部参数的量化,增加置信度矩阵,同时考虑参数灵敏度的影响。

1.2 Bayesian模型修正法[3-5]

先将模型修正问题转化为数学理论推导,利用泰勒级数格式展开,可以在满足精确度的情况下,适当略去高阶项

(1)

则模型修正的线性数学关系写成矩阵形式表示为

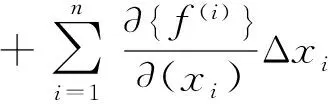
(2)

推出

(3)

进一步简化,写成矩阵形式

{Δf}=S{Δx}

(4)

(5)

式中，{Δf}为试验数据特征量与有限元模型特征量之差；{Δx}为修正后的参数与初始值之差；S为m×n维的灵敏度矩阵。在保证计算值满足足够精确度的情况下，{Δf}中取有限价，则{Δf}中只存在测试误差。可以进一步得出

{Δye}={ye}-{ye0}

(6)

在Bayesian的模型修正中,对矩阵{Δx}，{Δye}进行了假定,使其均服从均值为0的正态分布,而且彼此之间相互独立。{Δx}与{Δye}的联合概率密度为

(7)

又有[6]

E[{Δye}T{Δye}]=[Vy]，E[{Δx}T{Δx}]=[Vx]

(8)

E{Δye}=E{Δx}={0}，E[{Δx}T{Δye}]={0}

(9)

式中，[Vy]、[Vx]分别为{Δx}、{Δye}的协方差。联合概率安度的极大值等价于以下方程的极小值。

maxP(Δx，Δye)=minJ(x)=

{Δye}T[Vy]-1{Δye}+{Δx}T[Vx]-1{Δx}

(10)

将式(6)、式(8)、式(9)代入式(10),得

minJ(x)=E+{Δx}T{Δx}-1[{Δx}T]-1{Δx}

(11)

再用上式对{Δx}求导可得{x}

(12)

式中：y是设计参数变量x的函数,它可以是模态频率、振型、质量和刚度矩阵等，ye来源于试验取值。

1.3 试验与数值分析结果的相关性分析

置信度αmac用以表征试验与数值分析结果匹配性能的好坏,而且还能确定计算分析结果的误差准则。

振型相关系数计算公式为

(13)

将模型的试验结果与计算结果,在坐标系上,按横、纵坐标标出,并进行各阶模态频率的匹配。如果两者结果匹配比较好,则所有的点应该落在45度线上,如果落点有偏差,就说明有限元模型的设计相关参数存在误差[7]。

2 试验梁模态分析与有限元模型修正

2.1 试验桥梁模型简介

本次试验以太子河中华大桥为背景。大桥为预应力混凝土T型简支梁结构,共15跨,总长400.14m,宽13.2m,横向由6根T型梁并排连接。桥梁模型根据动力模拟准则,选用单跨T型梁为试验模型,对该桥进行静力加载和动力测试试验,利用本桥单跨有限元模型与动力试验数据来实现有限元模型修正。

2.2 模型细部结构修正

2.2.1ANSYS中钢筋混凝土模拟与混凝土本构关系

ANSYS软件有专门模拟混凝土结构的SOLID65单元,它能够模拟混凝土拉裂和压碎破坏特性。本文采用直观、便于理解的分离式方式建模,钢筋用LINK8单元模拟。根据相关研究,可以不考虑混凝土单轴应力—应变曲线的下降段[8]。

本文考虑两种本构关系模型,一种是ANSYS默认的理想弹塑性本构模型;另一种是多线性随动强化模型MKIN,且不考虑下降段;同时,采用拉应力准则和W—W五参数准则。

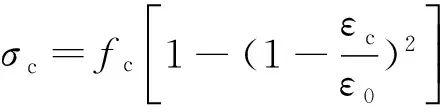
(14)

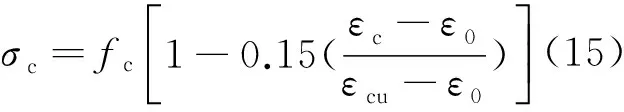
2.2.2 端部预应力筋的处理

采用降温法施加预应力,降温法的计算公式为

(16)

其中：T力筋施加温度值；σ为张拉控制应力；α为线膨胀系数；E为钢筋弹性模量。

在预应力的施加过程中,预应力损失值按《公路钢筋混凝土及预应力混凝土桥涵设计规范》[9](JTGD62-2004)规定计算,但还有一个重要的问题是,因为力筋施加预应力值很高,再加上极限受荷,会使力筋应力达到屈服,考虑到实际预应力的施加情况,在端部用锚具进行锚固,才使端部不会过早出现应力集中,而发生端部破坏。一般预应力混凝土结构的有限元模型较少考虑这一点,但在极限加载分析时,一定要考虑,并做相应处理。因此,本文在端部施加锚固钢板单元,见图1所示。

图1 端部预应力单元

然后,结构细部处理可以通过建立四组不同的有限元模型,先进行试验与有限元模型数据对比,得出最优结合,作为细部结构的修正结果。四种组合方式见表1。

表1 四种模型的组合方案

2.2.3 细部结构处理结果对比

其中,模型1和模型2没有进行端部锚固单元处理,使用正常无钢板的SOLID65单元,当进行预应力施加时,梁出现正常反拱,随着施加荷载不断增大,模型2在端部出现应力集中,过早发生破坏,计算不收敛;模型1和模型3为理想弹塑性本构模型,一般可以收敛,但计算值要比实际值大;而模型4采用多线性随动强化本构关系,并在端部做预应力处理的模型,计算结果与实际值吻合很好。四种方案与实测值的荷载—位移曲线见图2。

图2 四种方案与实测值的荷载—位移曲线对比

2.3 基于细部修正后的有限元模型修正

2.3.1 有限元模型设计参数的选择

有限元模型参数的误差一般是因为不确定或不精确的几何尺寸、材料属性和边界条件所引起。对于辽阳市中华大桥试验模型,部分结构参数可以通过设计资料得出,如混凝土强度等级、钢筋型号、设计截面、支座变形等,但是,桥梁长时间运行使混凝土强度降低,弹性模量发生变化,实际预应力大小比设计预应力要略小;同时,在建立有限元模型时,为了容易划分网格,需要对模型做细部的简化等,初步确定的模型修正参数及初始值列于表2。

表2 模型修正设计参数及初始值

2.3.2 有限元模型参数修正

有限元模型选择的修正参数不能过多,参数越多,计算量就会越大,可以凭借试验结果和经验,按照各参数对各阶模态灵敏度的大小,选择影响大的参数。但是,对于T型梁的弹性模量、质量密度、截面面积这三种基本物理参数对所有振型都会有影响,且其他一些参数如梁的截面抗弯惯性矩、预应力则分别对特定的振型产生影响。按照MAC准则对原始模型与测试模型进行各阶模态相关性分析,以保证两者振型匹配[10]。

以上参数的修正,按照模态频率的计算值与实测值之间的误差量作为迭代收敛准则,要求理论计算值与实测值误差不超过5%,第一阶频率误差小于1%。经过迭代计算,有限元模型频率计算结果列于表3,并与实测频率值进行比较。迭代修正后的结构参数值见表4。

表3 有限元模型频率计算结果

表4 结构参数修正结果

3 太子河中华大桥极限承载力计算

3.1 实桥有限元模型

太子河中华大桥单跨长为22.16m,由12片变截面预应力T型连接而成,各片梁之间由肋梁连接。该桥为双向6车道公路桥,中间有隔离带,双向通车为对称结构,因此,只建立1/2模型,分析其极限承载即可。

预应力钢束采用12φs5，标准抗拉强度为1 280MP,张拉控制力为53.46t。预应力的损失按照《公路钢筋混凝土和预应力混凝土桥涵设计规范》[9](JTGD62-2004)所规定的公式进行计算,其中包括:锚具变形、预应力筋的应力松弛,混凝土收缩等。同时,在试验模型修正参数的基础上,建立有限元模型见图3。

图3 有限元模型

3.2 加载

用有限元模型模拟实桥过车加载过程,按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》[9](JTGD62-2004)和《公路桥涵设计通用规范》[11](JTGD60-2004)两规范,加荷系数取1.0。

为了提高非线性分析的计算精度和便于收敛,要进行两项处理:第一,集中力加载点以均布荷载代替集中力,支座处采用线约束;第二,按照步骤施加荷载,先施加预应力荷载和桥面铺装结构恒载,然后按级加载,直至加载模型计算不收敛,即为结构破坏,达到极限承载状态。加载有限元模型见图4。

图4 有限元加载模型图

3.3 结果分析

在逐级加载的过程当中,桥梁的应力,应变和挠度会逐渐加大,当达到极限状态时,会突然不收敛,也就是由收敛到不收敛来判断极限状态是否达到。按照材料定义的本构关系,当到达极限状态时,荷载与挠度曲线会出现水平段,此时,结构产生很小的应力,将发生很大的挠度变化,即为极限荷载。荷载与挠度曲线见图5。

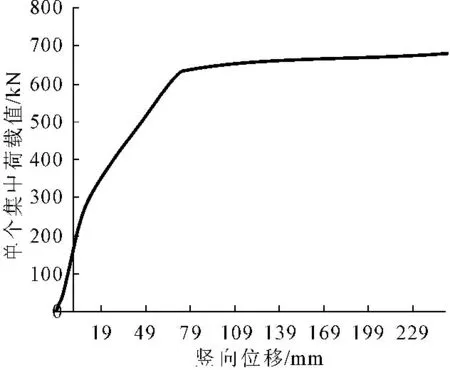
图5 荷载与挠度曲线

从图5中可以看出,按照车辆标准位置(前轮和后轮处按集中力F加载,如加载图中的红色位置即为集中力加载位置)逐级加载,当荷载逐渐增大挠度也增大,在上升阶段竖向位移f=11.794 mm,有一个横向的突变,这是混凝土发生开裂的正常表现,随后又以一定的斜率上升,预应力钢筋应力继续增大,当达到钢筋的屈服应力时,预应力筋产生大的应变,荷载—挠度曲线即出现水平段的极限荷载,此时,单个集中力F为643.24 kN。

4 结 论

(1) 考虑多参数的模型修正,克服了试验结构参数与数值模拟参数之间的误差,保证了建立模型的准确性,为桥梁模型的进一步分析打下基础。

(2) 对于大型结构分析,除有限元参数对结构模型产生影响外,结构细部“敏感”因素对结构模型影响亦很大,本文充分考虑了影响预应力钢筋混凝土结构的两大因素——钢筋混凝土结构本构关系和预应力的处理,得出了更加合理的修正参数。

(3) 以辽阳市太子河中华大桥为背景,并在此修正理论的基础上对其进行了极限承载力的分析计算,该成果对同类桥梁工程结构的承载力分析具有一定的参考价值和指导意义。

[1] 荣见华,郑健龙,徐飞鸿.结构动力修改及优化设计[M].北京:人民交通出版社,2002.

[2] 黄民水,朱宏平.基于不同残差的桥梁结构模型修正[J].武汉理工大学学报:交通科学与工程版,2009,33(4):703-706.

[3] Natke H G. Updating computational models in the frequency domain based on measured data: a survey[J]. Probabilistic Engineering Mechanics,1998,8(1):28-35.

[4] 李兆霞,李爱群,陈鸿天,等.大跨桥梁结构以健康监测和状态评估为目标的有限元模拟[J].东南大学学报:自然科学版,2003,33(5):562-572.

[5] 袁爱民.基于灵敏度分析的有限元模型修正技术若干关键问题研究[D].南京:东南大学,2006.

[6] 华宏星,傅志方.有限元模型修正中的Bayes方法的几点讨论[J].振动工程学报,1998,11(1):110-115.

[7] Ewins D J. Model validation: correlation for model updating[J]. Sadhana, 2000,25(3):221-234.

[8] 凌 广,吴同乐,贾永刚.钢筋混凝土有限元分析[J].工程结构,2003,23(5):51-53.

[9] 中华人民共和国交通部.JTGD62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京：人民交通出版社，2004.

[10] 郭 彤,李爱群,韩大章.基于灵敏度分析与优化设计原理的大跨桥梁动力模型修正[J].桥梁建设,2004,1(6):20-23.

[11] 中华人民共和国交通部.JTGD60-2004公路桥涵设计通用规范[S].北京：人民交通出版社，2004.

An Ultimate Bearing Capacity Analysis on Bridges Based on Model Updating

SONG Zhi, SUN Qiang

(LiaoningInvestigationandDesignInstituteofWaterResourcesandHydropower,Shenyang,Liaoning110006,China)

Regarding to the problem of large pre-stressed reinforced concrete structural bridges with structural damages, the finite element numerical analysis approach based on model updating was put forward. Large pre-stressed reinforced concrete structural bridges are complicated with long-span, multiple free degrees, multiple units and nonlinear characteristics, etc. So that the initial models established with finite element software are always insufficient. In order to create an accurate model that would reflect the structural characteristics of the bridges, finite element model updating theory was adopted to create a more suitable model with the consideration of the multiple factors. This new model revised the sensitive details of the structural design. Based on the study of Taizi River Zhonghua Bridge in Liaoyang, the calculation and analysis of its ultimate bearing capacity was conducted using the updated model. This approach will provide some guidance and reference for analyzing ultimate bearing capacity of similar bridge structures.

Taizi River Zhonghua Bridge; model updating; finite element simulation; ultimate bearing capacity

10.3969/j.issn.1672-1144.2015.05.045

2015-05-01

2015-05-25

宋 智(1973—)，男，辽宁沈阳人，高级工程师，主要从事水利工程、结构工程设计，以及管理方面的研究工作。 E-mail:9200315@163.com

U448.23

A

1672—1144(2015)05—0228—05