管道表面椭圆裂纹的断裂力学有限元分析

邵菁，张德琦，付路路, 孙海霞

（1. 辽宁石油化工大学 机械工程学院， 辽宁 抚顺 113001； 2. 山东华鲁恒升化工股份公司，山东 德州 253024）

管道表面椭圆裂纹的断裂力学有限元分析

邵菁1，张德琦1，付路路2, 孙海霞2

（1. 辽宁石油化工大学 机械工程学院， 辽宁 抚顺 113001； 2. 山东华鲁恒升化工股份公司，山东 德州 253024）

针对小裂纹断裂力学的基本概念，运用ANSYS workbench15.0有限元软件建立了压力管道及其裂纹的三维实体模型，并对其进行了有限元网格划分，最后对小裂纹进行了断裂力学计算，得出了裂纹的KⅠ强度因子、KⅡ强度因子、KⅢ强度因子和J积分，定量的分析了裂纹尖端区域的应力场强弱程度，为压力管道裂纹的研究提供了定的数据支持。

压力管道；裂纹；断裂力学；有限元

断裂是油气管道最为重要的一种失效形式。在实际管道构件中，管子制造、焊接、施工、应力腐蚀、疲劳等各种工作环境引起的裂纹大多都是非穿透裂纹，包括Ⅰ型裂纹、Ⅱ型裂纹、Ⅲ型裂纹和复合型裂纹[1]，而大多属于Ⅰ型裂纹（张开型裂纹），也就是最为危险的而一种裂纹形式，管道破裂以前表面裂纹发生失稳扩展，一旦发生破裂裂纹就会以穿透裂纹高速进行扩展，发生低应力脆断。

1 管道裂纹结构及相关参数[2]

管道长度为1 m，内半径为0.1 m，外半径为0.108 m，椭圆裂纹的计算参数为，椭圆短半轴a=0.006 m，长半轴b=0.05 m，裂纹位于管道的中部。具体结构图如图1所示，管道的材料为结构钢，弹性模量为2.1e11，泊松比0.29。

2 断裂力学计算

经有限元划分裂纹尖端网格如图2所示[3]。

图1 管道结构图Fig.1 Pipeline chart

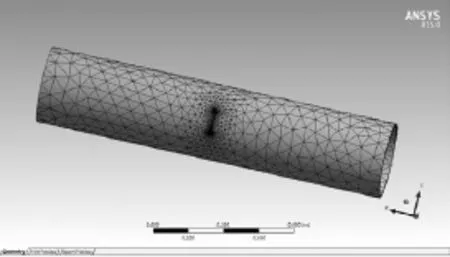
图2 裂纹尖端网格Fig.2 Crack tip mesh

施加约束和载荷条件为：完全约束管道的一侧，在管道的而另一侧施加裂纹的集中力10 000 N，同时施加一个扭矩M=1 000 N·m，以此为模拟边界条件，进行结果的断裂力学计算。

3 结果分析

经有限元模拟得出裂纹的等效应力云图如图 3所示[4]，由此可以得出，结构在此边界条件下，没有产生穿透裂纹，最大等效应力为206.62 MPa。

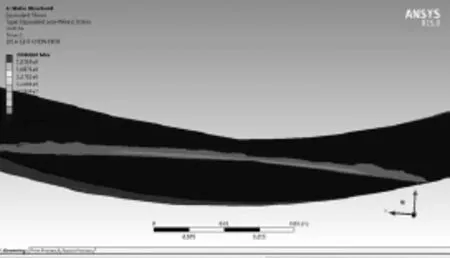
图3 裂纹尖端等效应力Fig.3 Crack tip equivalent stress map

由此得出裂纹的Ⅰ型强度因子如图4所示，最大值为2.47e6 Pa·m。

图4 KⅠ强度因子Fig.4 KⅠintensity factor

由此得出裂纹的Ⅱ型强度因子如图5所示，最大值为45 395 Pa·m。

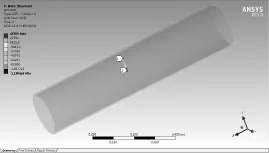
图5 KⅡ强度因子Fig.5 KⅡintensity factor

由此得出裂纹的Ⅲ型强度因子如图6所示，最大值为1.827e5 Pa·m。

由此得出裂纹的J积分如图7所示，最大值为26.77 J/m2。

由此可知，三种应力强度因子中Ⅱ型强度因子较小，因为在边界条件中没有平行于断裂面的剪切力，即断裂面产生很小的相对滑动，计算结果符合经典计算的理论值[5]。

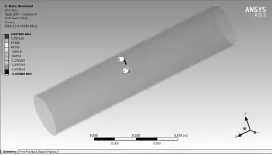
图6 KⅢ强度因子Fig.6 KⅢintensity factor

图7 J积分Fig.7 J integral

4 结束语

针对断裂力学计算过程中最为关键的有限元网格模型，本文给出了较为程序化的建模过程，即是采用裂纹、裂纹过渡和非裂纹等三大几何体，采用高质量的单元网格对裂纹尖端进行了细化，对其余结构进行相对的粗化。运用此方法创建了含椭圆表面裂纹的有限元模型，计算了结构在正应力作用和弯矩作用下的断裂力学参数 ，即Ⅰ、Ⅱ、Ⅲ型强度因子和J积分。

研究结果表明，对于弹塑性的材料，在结构承受没有发生大变形的载荷下，可采用应力强度因子K 或者J 积分作为评估标准[6-8]。断裂力学准则和失效云图相结合，可以进行含表面裂纹管道的安全评定。

本文计算的应力强度因子，主要是在线弹性的范围内进行计算的，对于弹塑性、塑性等相关问题并没有涉及，对管道结构断裂力学的计算仅仅包括裂纹的三种类型的应力强度因子和J积分，并没有进行结构损伤容限、裂纹扩展寿命和剩余强度等其他方面的研究[9-11]，这些问题在后续的研究中会作为重点分析课题。

［1］陆毅中.工程断裂力学[M].西安:西安交通大学出版社,1986:35-38.

［2］周继云, 张维,栾兴峰,等.管道弯管区裂纹的断裂力学参数 KJ 计算研究[J].核技术，2013,36（4）:1-6.

［3］何家胜, 朱光强, 朱晓明,等.弯扭组合载荷下圆管半椭圆表面裂纹应力强度因子的有限元分析[J].工程设计学报,2007, 14(2): 153-159.

［4］王荣荣,付路路,姜慧,等.基于事故树分析法的环氧乙烷生产中火灾爆炸事故分析[J].当代化工,2014,(4):598-599,602.

［5］王永伟, 林哲.表面裂纹的三维模拟及应力强度因子计算[J].中国海洋平台, 2006,26(3): 23-26.

［6］赵新伟,罗金恒,杨政,等.管线钢表面裂纹体的三维断裂特性和断裂判据研究[J]. 机械强度，2009,31(4):654-660.

［7］赵新伟,罗金恒,路民旭,等.管线钢断裂韧性和疲劳扩展特性研究[J].石油学报,2003,24(5):108-112.

［8］王荣荣,付路路,陈广芳,等.基于ANSYS的圆柱销装配预应力受力分析[J].当代化工,2014,(2):308-309.

［9］Nesterenko,GI.comparison of demage tolerance of integrally stiffened and riveted structures[C].ICAS 2000 congress United Kingdom, 2000.

［10］郭远帅.某无人机机翼断裂力学分析[D].南昌：南昌航空大学，2013-06.

［11］王冲,鲁统利.飞机蒙皮埋头钉孔裂纹扩展有限元分析[J].上海工程技术大学学报,2011,29(2):389-392.

Fracture Mechanics of Elliptical Crack on Pipe Surface With Finite Element Analysis

SHAO Jing1, ZHANG De-qi1, FU Lu-lu2, SUN Hai-xia2
（1. School of Mechanical Engineering, Liaoning Shihua University, Liaoning Fushun 113001, China；2. Shandong Huaneng Power Chemical Corporation, Shandong Dezhou 253024，China）

Based on the basic concepts of fracture mechanics for small cracks, a three-dimensional solid model of pressure pipes and cracks was established with the finite element software ANSYS workbench15.0, and finite element meshing was carried out, and finally mechanics calculation for the small cracks was conducted to obtain KⅠintensity factor, KⅡintensity factor, KⅢintensity factors and J integral, and stress field strength of the crack tip region was quantitatively analyzed, which could provide data support for piping crack research.

Pressure pipe; Crack; Fracture mechanics; Finite element

TE 832

A

1671-0460（2015）08-1972-02

2014-12-08

邵菁（1990-），女，天津汉沽人，硕士研究生，研究方向：煤炭生产安全。

张德琦（1963-），男，教授，研究方向：煤炭生产安全。