旋转挂片法测定水处理剂缓蚀性能的精密度分析

李亚红，元 昊，王 静，赵小芳，周 筝，王维珍

（国家海洋局 天津海水淡化与综合利用研究所，天津300192）

SW303是一种有机硫类非氧化性杀生剂，具有优良的杀菌灭藻性能［1］，近年来在沿海电厂的海水冷却水处理中得到了广泛试用，产品研制进入定型期。在产品定型过程中，拟采用GB／T 18175-2000《水处理剂缓蚀性能的测定 旋转挂片法》［2］作为评价其对金属腐蚀性能的测试方法。GB／T 18175-2000是测定水处理剂对金属是否具有缓蚀性能的方法标准之一，该标准采用旋转挂片失重法，通过测定金属试片在含有水处理剂的试验介质中的质量损失量来计算腐蚀率和缓蚀率，依此评价水处理剂对不同金属的缓蚀性能。GB／T 18175-2000以传统的“允许差”来判断测试结果的可靠性的。但随着GB／T 6379-2004（ISO 5725）《测量方法与结果的准确度（正确度与精密度）》［3］的发布实施，一些测试方法标准的制修订中更倾向于采用“精密度”代替传统的“允许差”。GB／T 6379-2004（ISO 5725）是关于分析和评价测试方法质量的一项重要的基础标准，该标准规定以精密度数值作为测试方法的质量指标，并规定方法的精密度可以重复性标准差sr、重复性限r和再现性标准差sR、再现性限R的形式获得估计。目前，采用重复性限和再现性限来表示方法的精密度，并在实践中判断分析结果的可靠性，已为国际标准和国外先进标准所广泛采用［4-7］。为考察采用GB／T 18175-2000测试杀生剂腐蚀性能的适用性，并尝试以“精密度”代替传统的“允许差”作为测试结果的质量评价指标，本工作按照GB／T 6379-2004，组织了杀生剂SW303对20号碳钢在海水中的缓蚀性能测试的精密度共同试验，并采用数理统计方法，估计了旋转挂片失重法的精密度。

1 试验

1.1 试片

试片为20号碳钢标准腐蚀试片（50mm×25mm×2mm），按照GB／T 18175-2000［2］对试验前、后的试片进行处理、称量。称量使用METTLER ALP204电子天平，精确至0.000 2g。

1.2 试验水质

试验用海水采自浙江象山港，水质分析结果见表1，分析方法参照GB／T 12763.4-2007［8］和GB／T 15452-2009［9］。

1.3 水处理剂

有机硫类非氧化性杀生剂SW303由天津市塘沽中海防腐技术开发公司提供。SW303的使用浓度为1mg／L、10mg／L、15mg／L和30mg／L。

表1 试验用海水水质Tab.1 Seawater quality in the tests

1.4 旋转挂片失重试验

按照GB／T 18175-2000［2］，应用SCC-Ⅱ型旋转挂片腐蚀试验仪进行旋转挂片失重试验，根据试验前、后试片的质量损失，计算腐蚀率和缓蚀率，评价杀生剂SW303的缓蚀性能。试验在（45±1）℃的海水中进行，试片转速为80r／min，试验周期72h。试片试验前未经预膜处理。直接向试验海水中投加使用浓度的SW303。

1.5 精密度试验安排

在确定旋转挂片失重试验方案后，在国内不同地区筛选5家实验室，并向其分发20号碳钢试片、海水、杀生剂SW303，要求各实验室按GB／T 6379-2004［3］规定，由同一名操作者按照试验方案，开展精密度共同试验。在重复性条件下，每个水平给出3～4个测试数据，小数点后保留3位小数。

1.6 测试数据的统计分析

共获得5家实验室、5个水平的92组腐蚀率数据。按照统计学方法［3，5］对以上数据进行统计检验。计算实验室内和实验室间的允许差［2］，运用曼德尔（Mandel）一致性检验统计量h和k检查是否存在测量精度和准确度上的异常实验室、柯克伦（Cochran）检验统计量C检验实验室单元方差的一致性、格拉布斯（Grubbs）检验统计量Gmax和Gmin检验实验室单元平均值的一致性。如测量有效，以重复性方差sr和重复性限r、再现性方差sR和再现性限R，及其与单元平均值m间的函数关系表示方法的精密度。

2 结果与讨论

2.1 各实验室最终报告结果的确定

GB／T 6379.1-2009规定“重复性”指“在重复性条件下的精密度”，“重复性条件”指“在同一实验室，由同一操作员使用相同的设备，按相同的测试方法，在短时间内对同一被测对象相互独立进行的测试条件”。“重复性限”指“一个数值，在重复性条件下，两个测试结果的绝对差小于或等于此数的概率为95%”，“重复性临界极差”指“一个数值，在重复性条件下，几个测试结果的极差以95%的概率不超过此数”。本次共同试验的5家实验室各水平下获得的测试结果数均＞2，按照GB／T 6379.6-2009对测试数据进行重复性统计分析，结果见表2。由表2可知，5家实验室内对同一样品的多次测试结果的极差（xmax-xmin）均小于临界极差CR0.95（n）。GB／T 6379.1-2009规定，同一实验室、同一样品多次测定结果的极差（xmax-xmin）均小于临界极差CR0.95（n）时，取测试结果的算术平均值作为最终报告结果。因此后续均取各实验室的算术平均值作为最终报告结果。

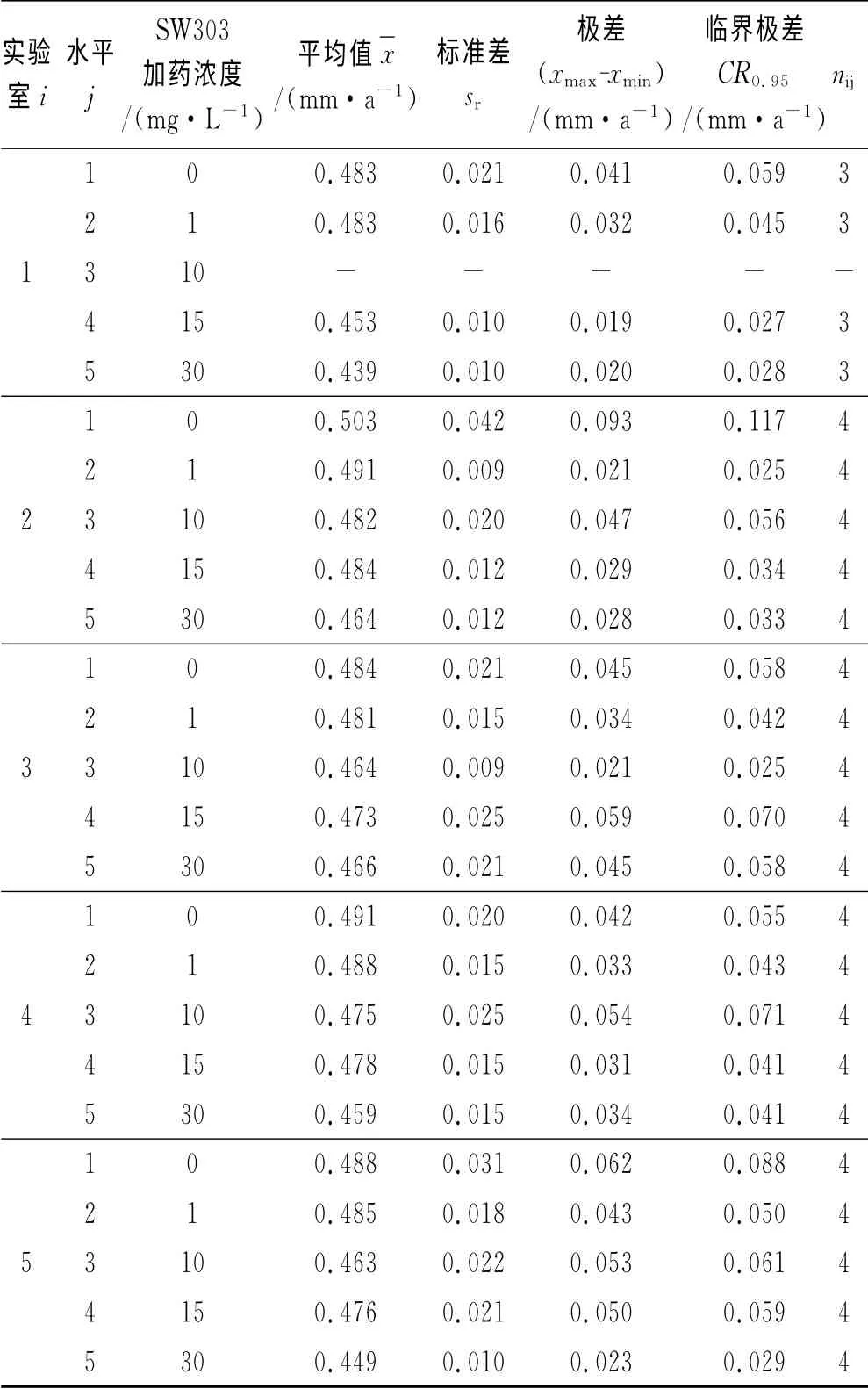
表2 实验室内重复性分析Tab.2 Analyses of repeatability in-laboratory

2.2 测试数据的相对偏差

GB／T 18175-2000规定，旋转挂片法的允许差为以单个平行测定结果与三片以上平行测定结果的算术平均值间的相对偏差不超过±10%。汇总数据后计算每个实验室、每个水平上的平行测试结果的相对偏差。实验室1在5个水平上的相对偏差在-4.90%～3.59%，实验室2在-8.66%～9.85%，实验室3在-6.76%～5.71%，实验室4在-5.91%～6.01%，实验室5在-6.10%～6.61%，均未超过±10%。

按照各实验室最终报告结果，计算不同实验室间不同水平的相对偏差在-1.70%～4.19%，也未超过的±10%允许误差，在可接受范围内。

2.3 测试数据的统计学分析

数据的分析是一个统计问题，涉及的统计量有重复性方差sr2、重复性限r、实验室间方差sL2、再现性方差sR2、再现性限R和平均值m。数据分析过程包括三个步骤：

（1）对数据进行检查，以判别和处理离群值或其他不规则数据；

（2）对每个水平分别计算精密度和平均值的初始值；

（3）确定精密度和平均值的最终值，且分析表明精密度和水平m之间可能的某种关系［1］。对数据进行检查的方法有检验一致性的图方法和检验离群值的数值方法。

2.3.1 检验一致性的图方法

检验一致性的图方法有曼德尔h图和k图、单元平均值直方图和单元极差直方图等。本工作采用曼德尔h图和k图法。其中，h是检验实验室间一致性的统计量，k是检验实验室内的一致性的统计量。h和k统计量除用来描述测量方法的变异外，对实验室评定也是有用的［3］。检查h图和k图，可以发现是否有测试结果与所考察的其他实验室明显不同的实验室。

按照GB／T 6379.2-2009中曼德尔统计量的计算公式计算各水平和各实验室的实验室间一致性统计量hij和实验室内一致性统计量kij，结果见图1。水平线分别表示了显著性水平为1%和5%的曼德尔统计量hij和kij临界值相对应的临界线。h图和k图显示，本次共同试验的5家实验室均未出现多个单元方差或单元平均值极端值，但h14超出了5%的h临界值，该数据是否为歧离值或离群值，还需进行单元方差一致性检验和单元平均值一致性检验。

2.3.2 检验离群值的数值方法

样本中的一个或几个观测值，它们离开其他观测值较远，暗示它们可能来自不同的总体，称为离群值（outlier）。离群值按显著性的程度分为岐离值（straggler）和统计离群值（statistical outlier）。统计离群值指剔除水平（α＝0.01）下统计检验为显著的离群值，岐离值指检出水平（α＝0.05）下显著，但在剔除水平下不显著的离群值［10］。

2.3.2 .1柯克伦（Cochran）检验

GB／T 6379.2-2009假定相对于实验室间而言，实验室内方差很小。但是经验表明实际情况并非总是如此，为此需对此假定的有效性进行检验。柯克伦检验是一种等方差检验，适用于实验室内单元方差的一致性检验。柯克伦检验针对的是一组标准偏差中的最大值，因此是一种单侧离群值检验。当然，方差不齐也包含标准差相对较小，然而小的标准差值可能很大程度受原始数据修约程度的影响，因而并不可靠。另外，似乎也没有理由拒绝一个比其他实验室精密度都要高的实验室数据。因此柯克伦检验是合理的。计算柯克伦统计量C，结果列于表3。

图1 按实验室进行分组的实验时间一致性曼德尔统计量Fig.1 Mandel statistics for the consistency of the laboratory unit average grouped by laboratories（a） hgraph （b） k graph

表3 单元方差的柯克伦检验统计量C值Tab.3 Cochran test′s Cvalues of the unit variance

当n＝3，p＝5时，显著性水平为5%的柯克伦检验临界值为0.684；显著性水平为1%的临界值为0.788；当n＝4，p＝5时，5%的临界值为0.598；1%的临界值为0.696。各水平的C值均小于1%和5%的临界值，未发现岐离值或离群值。

2.3.2 .2格拉布斯（Grubbs）检验

格拉布斯检验法是在未知总体标准偏差σ（x）的情况下，对正态样本或接近正态样本异常值进行判别的一种方法。当n较小时，格拉布斯检验法具有判定离群值的功效最优性［10］。对于测量次数n＝3～5的测量，格拉布斯检验理论较严密，概率意义明确，实践证明是一种比较切合测量实际的判别异常值的方法。相对于柯克伦检验而言，格拉布斯检验应用于实验室间单元平均值的一致性检验。表4给出了各水平的双侧格拉布斯统计量Gmax和Gmin。对一个离群观测值的格拉布斯检验，G大于临界值的为岐离值或离群值；对两个离群观测值的格拉布斯检验，G小于临界值为岐离值或离群值。在水平3的双高检验中，Gmax小于临界值，说明出现了成对岐离值，这对岐离值出现在的实验室2和4，但曼德尔和柯克伦检验对这两个实验室均未提出质疑，且未出现离群值，因此保留这对岐离值。其余各水平均未发现有单个或成对岐离值或离群值的存在。

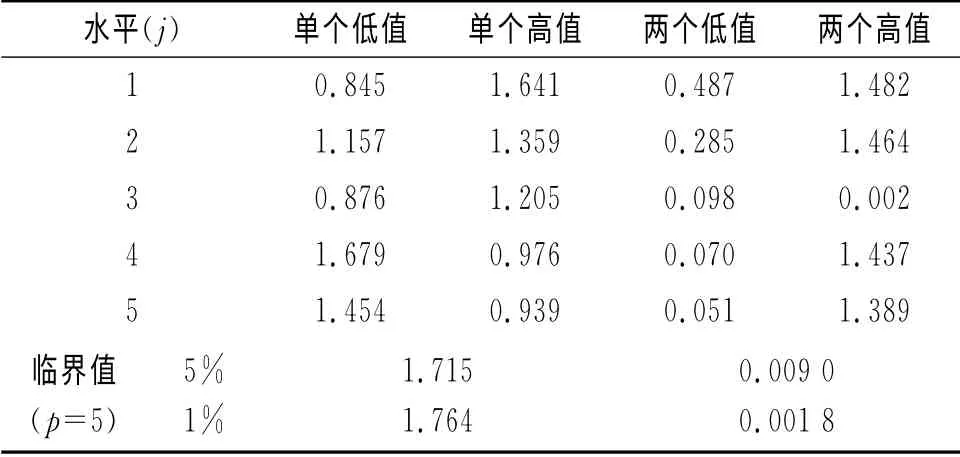
表4 单元平均值的格拉布斯检验统计量G值Tab.4 Grubbs test′s Gvalues of the unit average

2.3.3 精密度与总平均值m的关系

测量方法的精密度由sr（重复性标准差的估计值）和sR（再现性标准差的估计值）表示［1］。考察srj和sRj，及r和R与m之间是否存在某种函数关系，可确定方法的精密度是否依赖于m。

虽然在上述曼德尔和格拉布斯检验中发现了岐离值存在，但没有离群值，因此所有实验室的原始测试数据均予保留。对于每个水平计算总平均值m、方差（srj和sRj）、重复性rj和再现性限Rj，结果见表5。分别对sr、sR、r和R与m进行相关性分析显示，线性及非线性拟合曲线的相关系数r＝0.624 5～0.741 8（p＝0.18），无统计学意义，因此该方法的精密度与m之间不存在明显的依赖关系。就实际应用而言，方法的精密度可以用这些统计量的平均值来估计，即：

重复性标准差：sr＝0.005 1；

重复性限：r＝0.037；

再现性标准差：sR＝0.078 7；

再现性限：R＝0.045。

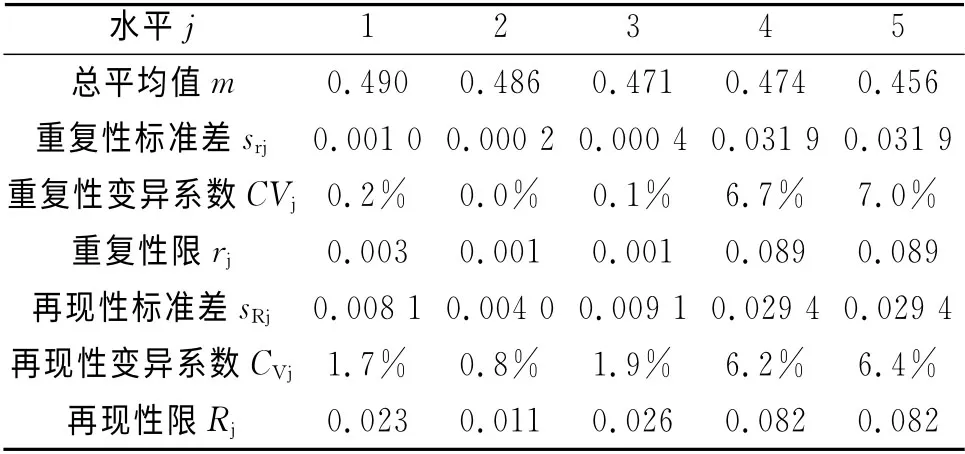
表5 测试方法的精密度Tab.5 Precision of test methods

2.4 SW303在海水中对20＃碳钢的缓蚀性能评价

鉴于共同试验的测试数据具有良好的重复性和再现性，因此可以根据这些数据评价SW303对20号碳钢的缓蚀性能。图2（a）显示，投加SW303前试片的腐蚀速率（P1）高于投加不同浓度SW303后试片的腐蚀速率（P2），判定SW303对20号碳钢有缓蚀作用，且碳钢试片的缓蚀率（y）和SW303的投加浓度（x）间呈良好的相关性（r＝0.966 9，p＜0.01），线形拟合方程为y＝0.551 46-0.216 83x（见图2b）。

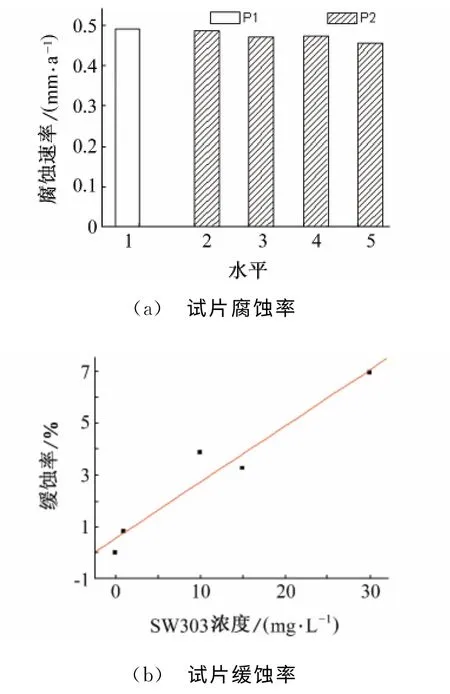
图2 20号碳钢在含SW303的海水中的腐蚀性Fig.2 Corrosivity of 20＃carbon steel in seawater containing SW303（a） Test coupon′s corrosion rate（b） Test coupon′s inhibition rate

3 结论

（1）虽然传统的允许差评价结果和数值的统计学检验结果略有差异，但最终结论一致，即本次精密度共同试验的所有测试数据均具有良好的一致性。此外，通过统计学检验，可以对数值的离散性给出更为详细的信息，即对异常值的显著性程度及其取舍均有了更为明确的依据，据此估计的方法的精密度相对于允许差来说，显见更具有统计学意义。

（2）SW303在海水中对20号碳钢的腐蚀进程无加速作用，且表现出微弱的缓蚀作用。这种缓蚀作用随SW303投加浓度的增大而增强。分析认为，SW303对碳钢的缓蚀机理主要是由于其对细菌具有杀灭作用［11］，导致试验水中细菌数减少，试片表面沉积的细菌量随之减少，从而降低了微生物诱导腐蚀，最终表现为碳钢腐蚀的减缓，且由于SW303的杀菌性能具有浓度效应，因此SW303对碳钢的缓蚀性能也表现出明显的浓度效应。

［1］陈冲，侯纯扬，李亚红，等.季铵盐及SW303对明亮发光杆菌和蒙古裸腹溞的毒性研究［J］.海洋环境科学，2013，32（2）：267-270.

［2］GB／T 18175-2000 水处理剂缓蚀性能的测定 旋转挂片法［S］.

［3］GB／T 6379-2004（ISO 5725） 测量方法与结果的准确度（正确度与精密度）［S］.

［4］闻向东，邵梅，曹宏燕.测量方法精密度共同试验测量数据的统计分析［J］.中国无机分析化学，2014，4（1）：69-75.

［5］徐本平.精密度试验中的数据处理［J］.冶金分析，2013，33（11）：74-80.

［6］王占明，李巨军.专用采样方案设计中几个要素的确定［J］.媒质技术，2014（1）：62-64.

［7］宋丽莎，王德章.火电厂水汽试验方法标准中允许差分析［J］.华东电力，2007，35（4）：80-83.

［8］GB／T 12763.4-2007 海洋调查规范 第4部分：海水化学要素调查［S］.

［9］GB／T 15452-2009 工业循环冷却水中钙、镁离子的测定EDTA滴定法［S］.

［10］GB／T 4883-2008 数据的统计处理和解释 正态样本离群值的判断和处理［S］.

［11］陈冲，侯纯扬，李亚红，等.一种杀生剂在海水介质中的降解行为研究［J］.水处理技术，2007，33（12）：58-61.