基于选权迭代的总体最小二乘算法在三维坐标转换中的应用
2015-02-15高井祥李增科
徐 波 高井祥 李增科 刘 洋
1 中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室,徐州市大学路1号,221116
在进行三维坐标转换时,利用LS 算法求解转换参数只考虑观测向量中的误差,而没有考虑系数矩阵中的误差。总体最小二乘(TLS)算法将观测向量和系数矩阵中的误差都考虑在一起。文献[1-2]介绍了总体最小二乘算法在坐标转换中的应用,并与最小二乘算法进行比较,认为TLS算法较LS算法更加合理。但是当控制点中存在粗差时,LS 和TLS 都不能得到有效的参数值。将抗差理论与LS和TLS相结合,可有效定位存在粗差的控制点,并对粗差控制点进行定权,求得未知参数值[3]。本文根据实例得出,基于抗差的LS算法和基于抗差的TLS算法能够得到有效的未知参数,但是抗差TLS 较抗差LS 收敛更快,并且随着存在粗差控制点数目的增加,TLS算法优势更明显。
1 坐标转换模型
空间三维坐标转换通常采用七参数模型:

式中,[XT YT ZT]T和[XS YS ZS]T分别是控制点在目标坐标系和原坐标系的空间三维坐标,[ΔX ΔY ΔZ]T为平移参数,[εX εY εZ]T为旋转参数,μ为尺度参数[1,4]。
当控制点数目大于2时上式的线性模型为:
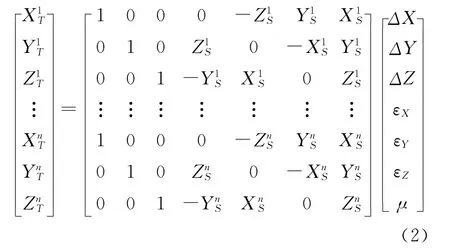
2 模型参数解算方法
2.1 最小二乘与总体最小二乘算法
当观测数大于必要观测数时,可以根据最小二乘算法求解未知参数的最优解[2]。但最小二乘算法只考虑了观测量的误差,没有考虑系数矩阵的误差,在解决高精度坐标转换时严密性较差。
总体最小二乘算法在最小二乘算法基础上,将系数矩阵的误差加入到平差过程中:

vec(ΔB)为矩阵的列向量,ΔB、ΔL为随机误差矩阵。式(3)可以化为:


对式(5)采用奇异值分解SVD 来求解参数的TLS解。求出未知参数X的估值其 中为矩阵[B,L]T·个特征向量组成的正交矩阵。单位权方差及参数的协方差矩阵为:

利用总体最小二乘算法求解空间三维坐标转换参数时,可以有效地控制观测量和系数矩阵的误差,求得未知参数的最优解。但是,当控制点坐标含有粗差时,仅利用总体最小二乘算法并不能有效地定位并剔除含有粗差的控制点,需要将抗差和总体最小二乘算法联合起来[5-9]。
2.2 基于选权迭代的总体最小二乘算法
基于选权迭代的总体最小二乘算法的关键在于定权,定权的方法有Hample权函数、周江文(IGG)权函数、Hubert权函数等。试验证明,在参数选取合理且粗差大于最小可探测偏差时,利用上述几种选权函数并根据本文的抗差TLS方法探测和定位粗差均能达到要求[10]。
借助IGG I权函数,并取k0=max(abs(v(i))/σ,为防止由于k0取值原因而产生秩亏现象,若k0=max(abs(v(i))/σ就不会剔除任何观测值,取权函数为,σ为方差因子,式中取k0=3.0。
将IGG I权函数和总体最小二乘算法结合起来,IGG I权函数需要分别对观测值向量和系数矩阵求权。设系数矩阵B的权为,观测向量L的权为,表示为:

设原坐标系和目标坐标系下观测值的协因数阵分别为Q1和Q2,对应的权阵为P1和P2。假设控制点i在原坐标系和目标坐标系下的坐标分别为和,对应的随机误差分布为和,则坐标变化关系式可以表示如下:

因此可以将误差向量v写成如下形式:
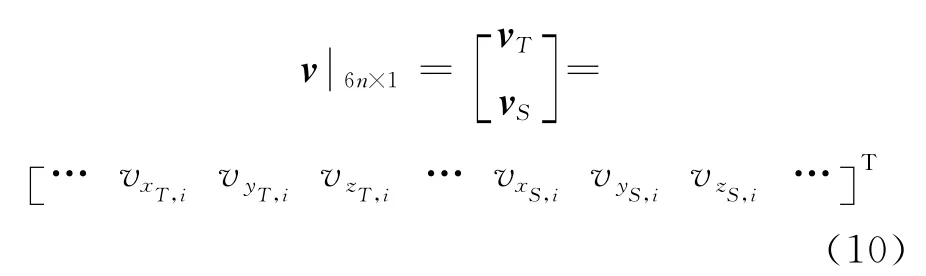
则选权迭代的总体最小二乘方程式可以写成:

坐标转换方程式可以写成:

设误差向量和未知参数的初值分别为v0和ξ0,对上式线性化得:
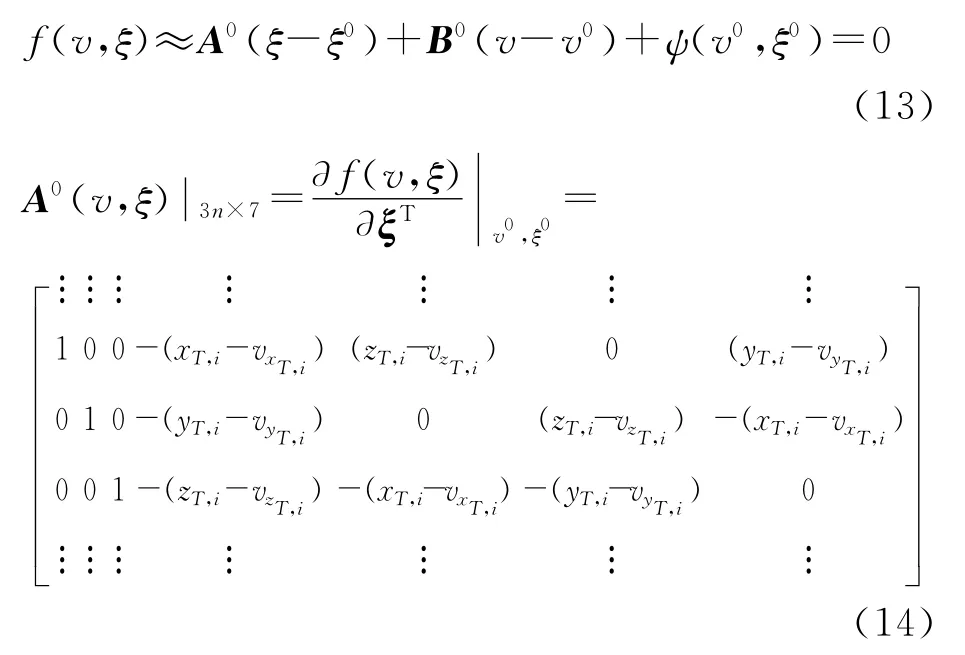


可以求得未知参数和拉格朗日乘数的改正数为:

通过迭代计算直到参数向量满足‖ξv-ξv-1‖≤η即可,通常取η=10-10。
3 算例分析
为验证基于选权迭代的总体最小二乘算法在求解三维坐标转换参数中的优越性,随机生成10个点。设七参数为(ΔX,ΔY,ΔZ)=(100,50,20),(ωx,ωy,ωz)=(10,15,20),旋转参数单位为(″),μ=1.001,在原坐标系统中的位置和转换后在目标坐标系中的位置可以在图1、图2看出。
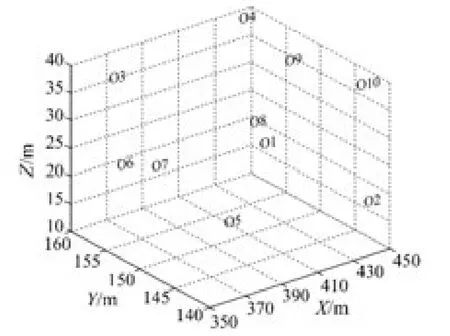
图1 控制点在原坐标系中的分布Fig.1 The distribution of the control points in the original coordinate system
给2号点在原坐标和目标坐标中分别加入粗差(0.5,0.5,0.5)和(-0.5,-0.5,-0.5),分别用上述方法算出两套坐标的转换参数(表1)。
由表1看出,当控制点存在粗差时,利用LS和TLS算法求解三维坐标转换参数会出现数值失真的情况,而抗差LS和抗差TLS算法求解的未知参数与真值相近。在收敛速度方面,抗差TLS算法的收敛速度较抗差LS算法快[10]。

图2 控制点在目标坐标系中的分布Fig.2 The distribution of the control points in the target coordinate system

表1 1个点存在粗差时4种方法计算出的转换参数Tab.1 Four methods to calculate the conversion parameters when one-point with gross errors
假设有2个控制点存在粗差,将2号点和8号点分别在原坐标和目标坐标中加入粗差(0.5,0.5,0.5)和(-0.5,-0.5,-0.5),并进行计算(表2)。

表2 2个点存在粗差时4种方法计算出的转换参数Tab.2 Four methods to calculate the conversion parameters when two-point with gross errors
表2同样反映出,当控制点存在粗差时,LS和TLS算法求解三维坐标转换参数会出现失真情况,抗差LS和抗差TLS算法求解的转换参数与真值差值较小。
假设有5个控制点存在粗差,将2、5、6、8、9号点在原坐标和目标坐标中分别加入粗差(0.5,0.5,0.5)和(-0.5,-0.5,-0.5),并进行计算(表3)。
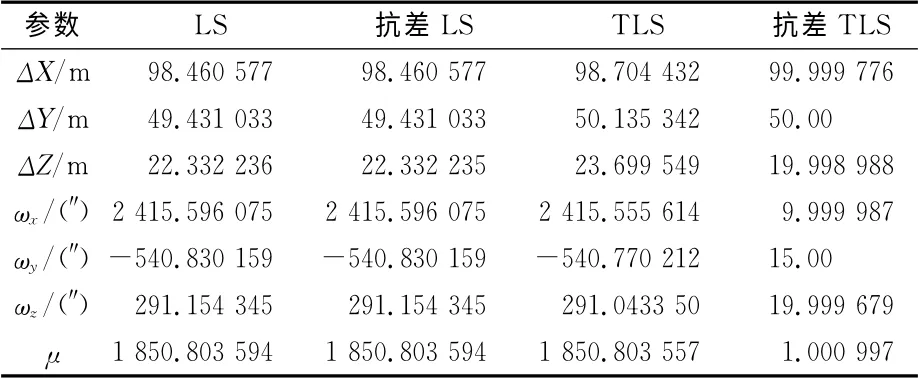
表3 5个点存在粗差时4种方法计算出的转换参数Tab.3 Four methods to calculate the conversion parameters when five-point with gross errors
表3同样反映了表1、2中LS和TLS存在的问题,但是随着存在粗差的控制点数目的增加,抗差LS算法求解的三维坐标转换参数与真值之差也变大,而抗差TLS算法求解的未知参数并没有明显变大,表明随着存在粗差的控制点数目的增加,抗差TLS算法较其他3种方法更加有效。
4 结 语
1)当控制点存在粗差时,利用LS和TLS求解转换参数时会发生严重的失真,而利用抗差LS和抗差TLS求解参数能够有效消除粗差对转换参数的影响。通过模拟数据分析,基于抗差TLS求解转换参数比基于抗差LS求解的效果更好一些。
2)随着存在粗差控制点数目的增多,LS、抗差LS和TLS所计算出的转换参数与真值的偏差越来越大,根据IGG I的定权结合TLS算法计算出的转换参数无明显变化。
3)对于空间转换模型而言,需要控制点在参心坐标系下的三维空间直角坐标求解模型参数。由于参心坐标系是通过光学观测建立的,控制点缺乏精确的大地高信息,使得控制点在参心坐标系下的空间三维直角坐标无法精确得到。这方面的问题还需继续研究。
[1]施一民.现代大地控制测量[M].北京:测绘出版社,2003(Shi Yimin.Modern Geodetic Control Survey[M].Beijing:Surveying and Mapping Press,2003)
[2]Golub H G,Vanl F C.An Analysis of the Total Least Squares Problem[J].SIAM Journal on Numerical Analysis,1980,17(6):883-893
[3]周江文.经典误差理论与抗差估计[J].测绘学报,1989,18(2):116-120(Zhou Jiangwen.Classical Theory of Errors and Robust Estimation[J].Acta Geodaetica et Cartographica Sinica,1989,18(2):116-120)
[4]陶本藻,邱卫宁.误差理论与测量平差基础[M].武汉:武汉大学出版社,2010(Tao Benzao,Qiu Weining.Error Theory and Fundation of Surveying Adjustment[M].Wuhan,Wuhan University Press,2010)
[5]黄令勇,吕志平,任雅奇,等.多元总体最小二乘在三维坐标转换中的应用[J].武汉大学学报:信息科学版,2014(7):793-798(Huang Lingyong,LüZhiping,Ren Yaqi,et al.Application of Multivariate Total Least Square In Three-Dimensional Coordinate Transformation[J].Geomatics and Information Science of Wuhan Unversity,2014(7):793-798)
[6]Tao Y Q,Gao J X,Yao Y F.TLS Algorithm for GPS Height Fitting Based on Robust Estimation[J].Survey Review,2014,46(336):184-188
[7]王乐洋,许才军.总体最小二乘研究进展[J].武汉大学学报:信息科学版,2013,38(7):850-856(Wang Leyang,Xu Caijun.Progress in Total Least Squares[J].Geomatics and Information Science of Wuhan Unversity,2013,38(7):850-856)
[8]杨仕平,范东明,龙玉春.基于整体最小二乘法的任意旋转角度三维坐标转换[J].大地测量与地球动力学,2013,33(2):114-119(Yang Shiping,Fan Dongming,Long Yuchun.Three-Dimensional Coordination Transformation Adapted to Arbitrary Rotation Angle Based on Total Least Squares Method[J].Journal of Geodesy and Geodynamics,2013,33(2):114-119)
[9]陆珏,陈义,郑波.总体最小二乘算法在三维坐标转换中的应用[J].大地测 量与地球动 力学,2008,28(5):77-81(Lu Jue,Chen Yi,Zheng Bo.Application Total Least Squares To Three Dimensional Datum Transformation[J].Geomatics and Information Science of Wuhan Unversity,2008,28(5):77-81)
[10]龚循强,李志林.一种利用IGG II方案的稳健混合总体最小二乘方法[J].武汉大学学报:信息科学版,2014,39(4):462-466(Gong Xunqiang,Li Zhilin.A Robust Mixed LSTLS Based on IGG II Scheme[J].Geomatics and Information Science of Wuhan Unversity,2014,39(4):462-466)
