最小二乘配置与REHSM 求解GPS应变场的方法

管守奎 瞿 伟 蒋 军

1 武汉大学测绘学院，武汉市珞瑜路129号，430079

2 长安大学地质工程与测绘学院，西安市雁塔路126号，710054

3 武汉大学GNSS中心，武汉市珞瑜路129号，430079

应变场是描述区域变形的一项重要指标。各国学者基于GPS观测资料对应变场开展研究，取得许多成果［1－5］。但是当研究区域仅有少量观测数据时，对应变场的精确求解就会变得困难，而最小二乘配置能够较好地解决观测数据较少的问题。本文提出使用刚体旋转模型（RRM），采用最小二乘配置解法获得较为充分的虚拟观测速度值，之后结合REHSM 方法，解决观测数据量较少时应变场的解算问题。

1 最小二乘配置与REHSM 解算应变场

1.1 REHSM 解算应变场

欧拉定理是现代板块运动定量描述的基本定理。如果把板块看成刚性，地球近似为球体，球心看成强制在地球表面运动的刚体板块运动的固定点，则地壳运动满足欧拉定理。设一点的经纬度为（λ，φ），则有：

式中，r为地球半径，Ve、Vn为站心参考系的经向和纬向速度，ωe、ωen、ωn为板块的旋转参数分量［6］。该式称为块体的刚体旋转模型（RRM）。

一个块体在周围块体作用下发生整体旋转的同时，内部也将发生应变。块体内部的应变可分解为两部分［7］：一是块体的纯应变，二是由应变引起的块体旋转。表示为：

x、y分别为观测点至研究区域中心经线与纬线间的平行圈弧长与子午线弧长，北东为正。εe、εen、εn分别是块体的东西向线应变、东西向和南北向之间的剪应变、南北向线应变。该式称为块体的整体旋转与均匀应变模型（REHSM）。

由上式可知，对于一个观测点，ε矩阵不能直接求得。本文对整个研究区进行栅格划分，以每个栅格4个顶点的速率信息求出的应变参数来代替栅格中心的应变参数。求得应变参数后，即可进一步计算应变场的特征值［8］。最大主应变率：

最大剪应变率：

面膨胀率：

1.2 最小二乘配置原理

最小二乘平差将所有待估参数当作非随机量，或不考虑参数的随机性质。最小二乘配置除包括经典最小二乘的非随机参数外，还包含随机参数，按照极大验后估计、最小方差估计或广义最小二乘原理求定参数的最佳估值［9］。函数模型为：

式中，Y′是非观测向量，在式（6）中其系数为0，并未包含在l内，而是依赖于协方差相联系，在对滤波模型作参数估计的同时对Y′进行推估。

配置模型的最优线性无偏估计为：

在最小二乘配置理论中，关键是求取已知点信号的方差－协方差矩阵、已知点信号与未知点信号的协方差矩阵。这两个矩阵都是由同一个协方差函数计算得到的，协方差函数选择恰当与否直接影响估计值的精度。本文分别采用以下6个协方差拟合函数进行计算。

1）多项式函数：

2）高斯函数：

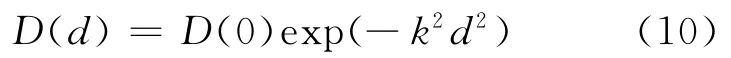
3）似高斯函数：

4）希尔沃宁函数：

5）空间调和函数：

Z＊＝Hi＋Hj，Hi、Hj为数据点的海拔高，考虑到d＝0的特殊情况，取Z＊＝｜Hi－Hj｜，但并不影响函数的对称、正定和协调性。该函数可以作为经验协方差函数：

式中，D为协方差，d为两测站点间的距离，D（0）为所有观测点方差的平均值，k为待定系数。通过不同的协方差拟合函数比较，获得最优的速度场拟合信息，为应变场的解算提供数据支持［10］。

2 计算实例

2.1 速度场构建

将位于运城盆地的基于“数字地震网络工程”的19个监测点分为两组，13个为已测点，6个为检核点。通过6种协方差拟合函数，比较获得最优的拟合方式。根据表1，采用希尔沃宁函数为协方差拟合函数时，E方向上为1.046 4mm／a，N方向上为2.009 6mm／a，两个方向的残差最大值均小于其他协方差拟合函数的结果。采用希尔沃宁函数为速率场构建时的协方差拟合函数，对所有的观测速度进行拟合，实测与拟合的速度场如图1，具体速度残差见表2。

由图1可直观看出，19个监测点的实测结果与拟合结果大小与方向较为符合。由表2 可看出，E方向上的残差绝对值最大值为0.775 6 mm／a，N方向为1.218 7mm／a，拟合结果良好。

表1 速率检核统计Tab.1 The statistics of velocity check

图1 实测速率与拟合速率比较Fig.1 Compared the measured velocity and fitted velocity

表2 速率拟合结果Tab.2 The result of velocity fitting

协方差拟合函数确定后，根据最小二乘配置方法构建的速率场信息如图2。由图2 可知，速度场拟合结果比较紧密。研究区域SN 方向的速率较EW 方向小，整体为水平偏南走向，同武艳强［3］、李延兴［6］的结果基本一致。

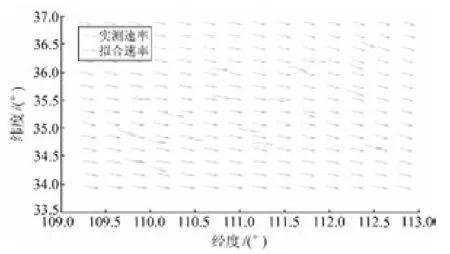
图2 拟合速率场Fig.2 Fitted velocity field

2.2 应变场构建

有了充足的速度信息，结合REHSM 与栅格化的解算方法，即可得到研究区域应变场特征参数的等值线图。

由图3～5 可以看出，高值区域主要分布在WS、EN 区域，低值区域主要分布在WN－ES 区域。高值区域为张性或应变率较为强烈的地区，数量级最大达1×10－8，反映这些区域是应变能高积聚区，发生中强地震的可能性较大。结合运城盆地的地质背景可知，WS、EN 区域为中条山断裂带，验证了应变参数求解的有效性。图6中黑色箭头为张性剧烈程度增加走向。可以看出，中条山断裂两侧向中条山区域两侧膨胀加剧，中条山两侧均受挤压，在碰撞处向WS、EN 两个方向释放能量，导致WS、EN 即中条山断裂走向区域张性提升。膨胀区域在膨胀交汇处，因各自膨胀方向均不相同，地壳运动活跃。据山西省地震局通报，2010－12－14 11：45在山西省运城市闻喜县、夏县交界发生3.3级地震，震中位于35.3°N、111.1°E。此区域正是图6中的椭圆区域，故而验证了该区域地壳运动的活跃性。

图3 面膨胀率等值线图Fig.3 The isogram of superficial expansion rate

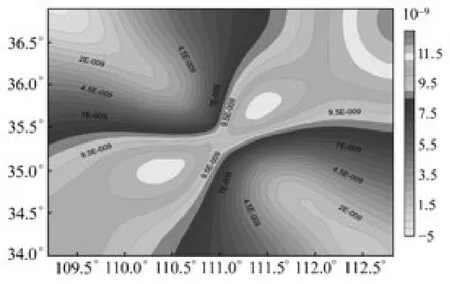
图4 最大剪应变等值线图Fig.4 The isogram of shear strain rate

图5 最大主应变等值线图Fig.5 The isogram of maximum principal strain rate

3 结 语

本文使用的地壳形变参数求解方法，能够有效解决监测点数据较少时应变场的解算问题。通过块体的刚体旋转模型，采用最小二乘配置以不同的协方差拟合函数获得较优的速率场，并同之前的全国性速度场结果进行比较。再将研究区域进行栅格化，通过块体的均匀旋转与应变模型，解决区域地壳应变场的求解问题。

图6 面膨胀率分析Fig.6 The superficial expansion rate analysis

［1］Dumak B S，Kotlia B S，Kumar K，et al.Crustal Deformation Revealed by GPS in Kumaun Himalaya India［J］.Journal of Mountain Science，2014（1）：41－50

［2］江在森，马宗晋，张希，等.GPS初步结果揭示的中国大陆水平应变场与构造变形［J］.地球物理学报，2003（3）：352－358（Jiang Zaisen，Ma Zongjin，Zhang Xi，et al.Horizontal Strain Field and Tectonic Deformation of China Mainland Revealed by Preliminary GPS Result［J］.Chinese Journal of Geophysics，2003（3）：352－358）

［3］武艳强，江在森，杨国华，等.利用最小二乘配置在球面上整体解算GPS应变场的方法及应用［J］.地球物理学报，2009（7）：1 707－1 714（Wu Yanqiang，Jiang Zaisen，Yang Guohua，et al.The Application and Method of GPS Strain Calculation in Whole Mode Using Least Square Collocation in Sphere Surface［J］.Chinese Journal of Geophysics，2009（7）：1 707－1 714）

［4］黄立人，王敏.中国大陆构造块体的现今活动和变形［J］.地震地质，2003（1）：23－32（Huang Liren，Wang Min.Present－Day Activity and Deformation of Tectonic Blocks in Chinese Continent［J］.Seismology and Geology，2003（1）：23－32）

［5］瞿伟，张勤，王庆良，等.渭河盆地现今地壳水平形变特征及区域构造活动性［J］.武汉大学学报：信息科学版，2011（7）：830－834（Qu Wei，Zhang Qin，Wang Qingliang，et al.Research on Present Crustal Horizontal Deformation Feature of Weihe Basin and Its Tectonic Activity［J］.Geomatics and Information Science of Wuhan University，2011（7）：830－834）

［6］李延兴，李智，张静华，等.中国大陆及周边地区的水平应变场［J］.地球物理学报，2004，47（2）：222－231（Li Yanxing，Li Zhi，Zhang Jinghua，et al.Horizontal Strain Field in the Chinese Mainland and Its Surrounding Areas［J］.Chinese Journal of Geophysics，2004，47（2）：222－231）

［7］许才军，张朝玉.地壳形变测量与数据处理［M］.武汉：武汉大学出版社，2009（Xu Caijun，Zhang Chaoyu.Crustal Deformation Measurement and Data Processing［M］.Wuhan：Wuhan University Press，2009）

［8］瞿伟.基于GPS速度场分析研究青藏块体东北缘的形变特征［D］.西安：长安大学，2008（Qu Wei.The Deformation Characteristic of the Northeastern Margin of Qinghai－Tibet Plateau Constrained by GPS Observations［D］.Xi’an：Chang’an University，2008）

［9］崔希璋，陶本藻.广义测量平差［M］.北京：测绘出版社，1992（Cui Xizhang，Tao Benzao.Generalized Survey Adjustment［M］.Beijing：Surveying and Mapping Press，1992）

［10］李冲，李建成，瞿伟.基于移动原理的拟合推估模型建立区域地壳运动速率场［J］.大地测量与地球动力学，2012（5）：33－36（Li Chong，Li Jiancheng，Qu Wei.Establishing Regional Crustal Movement Velocity Field with Collocation Based Displacement Principle［J］.Journal of Geodesy and Geodynamics，2012（5）：33－36）