软土地层TBM 开挖面支护压力计算模型及可视化

张子新 ，张 帆

（1.同济大学 地下建筑与工程系，上海，200092；2.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116）

1 引 言

TBM（tunnel boring machine）作为一种专门用于开挖地下通道工程的大型高科技施工装备，以其高效、安全、环保等优点，自20 世纪70年代以来，已越来越广泛地应用于国内外的地铁、城市给排水、铁路、公路等重大工程建设中。

TBM 按照掘进地层可分为岩石隧道掘进机和软土隧道掘进机（盾构机）。对于软土隧道掘进来说，开挖面支护压力的大小直接影响着开挖面的稳定和地表变形，对于保证施工安全及控制对周边环境的影响十分重要。因此，确定合适的开挖面支护压力，历来都是软土TBM 隧道施工中的一个重要问题。

目前，国内外学者从微观、宏观角度对开挖面失稳机制进行了分析，提出了许多开挖面失稳模型及支护压力计算方法。

微观失稳理论以土体颗粒单元为对象进行失稳机制研究。其中较为著名的有Davis 等[1]提出的评价开挖面局部稳定的模型及李昀[2]在该模型基础上考虑开挖面支护压力梯度的改进模型。

宏观失稳理论基于极限分析理论对开挖面破坏机制进行研究。其中最为经典的是Horn 提出的三维楔形体模型[3]，后续学者提出的锥体失稳模型[4]、M-M 模型[5]、圆台-转角模型[6-7]诸多改进模型大多基与此。

然而，尽管目前已有诸多相关计算模型，但大多数方法对应的计算过程都极为繁琐，且局限于特定的地层环境条件，缺乏普遍适用性，难以广泛地应用到实际工程中。因此，探究一种高效、便捷的方法，通过已有的计算模型及理论实现对实际工程中开挖面支护压力的计算，以更好地对比各计算方法的优缺点及改进其适用性，对于更好地理解开挖面物理力学特性及指导实际施工都具有十分重要的意义。

基于此，本文针对软土地层TBM 开挖面支护压力精确计算的难题，充分考虑复合地层特点及TBM 开挖面的失稳破坏特征，采用改进的三维楔形体模型、M-M 模型以及圆台-转角模型进行了复合地层TBM 开挖面支护压力的可视化计算，实现了工程参数的便捷输入及开挖面支护压力的高效计算。并结合实际工程实例，分析了不同计算方法在不同地层条件下的适用性，讨论了土体自稳性对开挖面稳定支护压力的影响。

2 软土地层开挖面支护压力计算方法

根据开挖面失稳破坏机制的不同，开挖面支护压力的计算模型主要分为微细观分析模型和宏观力学分析模型，本文重点分析工程尺度的宏观模型。其中，宏观力学分析模型中最为著名的是1961年由Horn 提出的三维楔形体模型[3]（见图1），该模型力学概念明确，简单实用。但只适用于砂性土地层的开挖面支护压力计算，对于黏性土地层的计算误差较大。

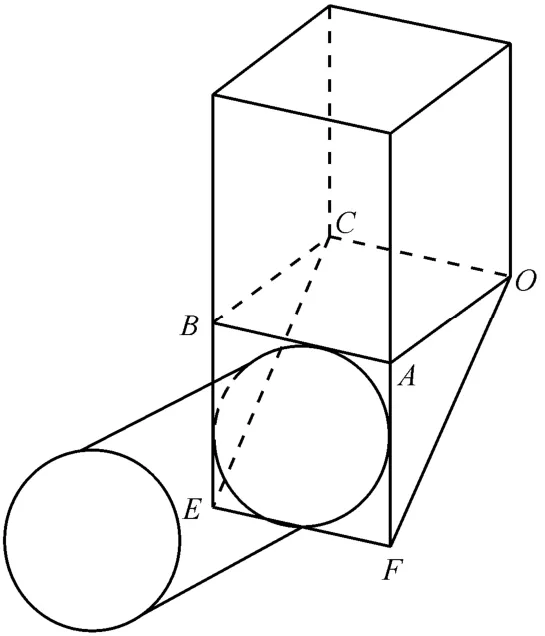
图1 Horn 三维楔形体模型Fig.1 Horn's three-dimensional sliding wedge model

2.1 三维楔形体模型的改进

在Horn 的三维楔形体模型的基础上，许多后续学者对其进行了改进。例如，Jancsecz 等[8]在Horn模型的基础上进行了修正，考虑了楔形体上部土柱土压力拱的影响，并采用该模型来分析盾构隧道开挖面的极限支护压力；Anagnostou 等[9]假定泥膜不透水，研究了地层抗剪强度、地层渗透系数、泥水黏度、泥水重度、泥水压力、隧道几何尺寸及开挖面稳定安全系数的相互关系；同时，又基于Horn的楔形体模型，提出了在均质各向同性地层中，分别适用于土压平衡式盾构及泥水式盾构的三维开挖面稳定支护压力的计算方法[10-11]。

Broere[12]总结相关学者的模型，提出将上述计算模型拓展于成层地基条件下，分析泥水平衡盾构及土压平衡式盾构施工极限支护压力，并考虑了泥水渗入地层的时间效应及地下水渗流产生的渗透力作用对开挖面稳定安全系数的影响。但对于复合地层，尤其是上覆土体的扰动土压力影响尚缺乏深入的分析。

2.2 土体分层的考虑

上述模型大多都假定地层为单一、均质的土体，或通过按土层厚度加权的方法将复合地层转化为单一地层，缺乏对土体分层所带来影响的考虑。

胡欣雨等[5]基于已有学者的一系列离心机试验成果、数值模拟结果及工程实测数据，将土层分层情况及上部覆土层松动土压力的影响考虑在内，提出了分层楔形体模型（M-M 模型），并推导出其解析解。

Hu 等[6-7]基于国内外已有文献的试验、数值模拟及现场观测结果，针对黏性土开挖面支护压力计算问题，将Horn 三维楔形体模型修正为圆台-转角模型，并综合考虑塌落失稳及冒顶失稳两种破坏模式，给出了开挖面稳定支护压力的上、下限解。

2.3 开挖面支护压力计算公式

本文针对软土复合地层的特点，提出了改进三维楔形体模型、M-M 模型和圆台-转角模型（见图2～图4），并进行了比较分析。具体的模型和计算公式推导如下：

2.3.1 改进的三维楔形体模型

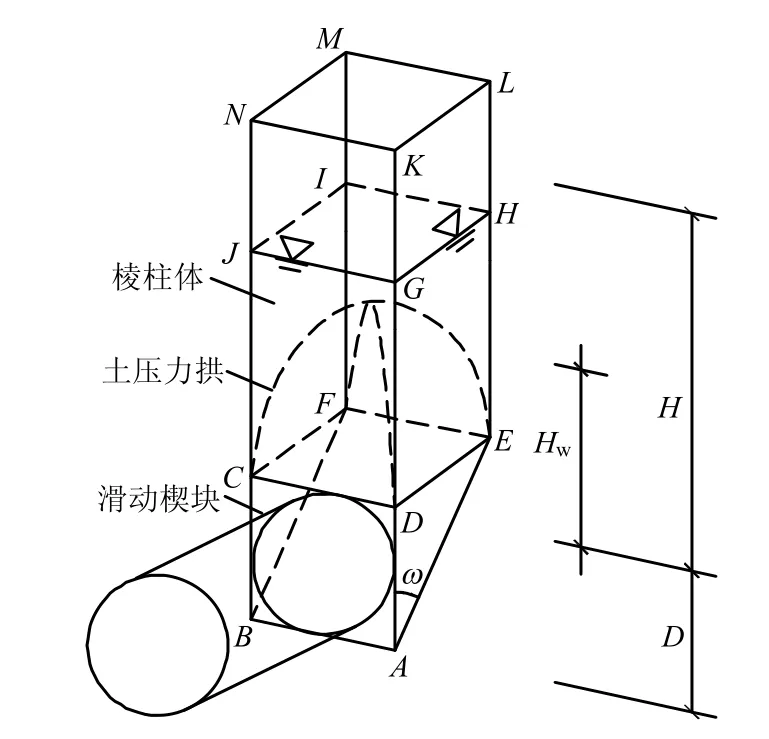
图2 改进的三维楔形体模型Fig.2 Modified three-dimensional sliding wedge model

该模型假定开挖面失稳的破坏机制为三维楔形体（见图2）。图中，H为覆土厚度，D为隧道开挖直径，Hw为地下水位标高，通过对极限状态下的滑动楔块进行受力分析，得出稳定开挖面的最小支护压力，计算公式为

式中：G为滑动楔块自重；V为棱柱体对滑动楔块的竖向作用力；T为斜滑动面ABFE 上的剪力；Ts为竖直滑动面ADE、BCF 上的剪力；ω为楔块滑移面与竖向平面的夹角；c为黏聚力。

通过变换ω 得到的P的极大值即为开挖面的临界支护压力下限解Pcr。

考虑到深埋隧道土拱效应的影响，竖向压力可按Janseen[13]提出的仓筒理论，并结合Terzaghi 竖向应力折减公式进行计算，即

对于复合地层，作用于滑动楔块上的竖向应力可通过逐层迭代进行求解。

如图3 所示，按覆土中土体类型将上部土柱划分成多段，对于每一层，都可以通过式（3）算得作用于下一层上部的竖向应力。

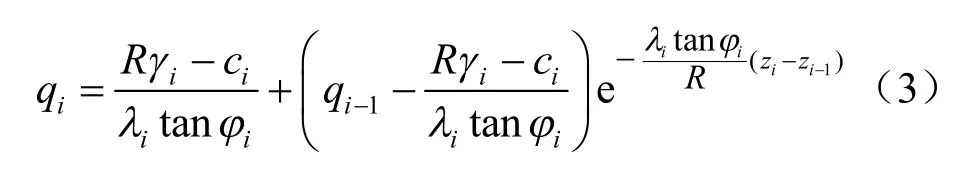
式中：i=1,2,…,n，其中n为覆土的层数；γi、ci、φi分别为第i 层土体的重度、黏聚力、内摩擦角；Zi1-、 Zi分别为第i 层土体上、下边界所对应的深度。

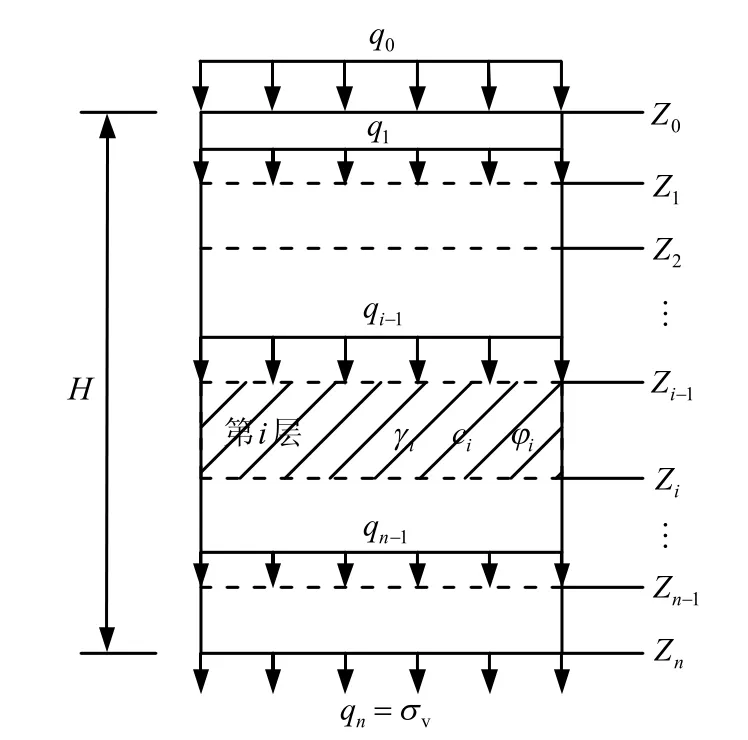
图3 竖向应力的迭代求解Fig.3 Iterative computation of vertical stress

该方法可以考虑覆土的分层，但对于楔块体部分仍按照均一化后的单一均质地层进行计算，因此，该模型较适用于均质地层。

2.3.2 M-M 模型

M-M 模型（modified wedge stability model and modified Terzaghi model），该模型考虑了开挖面失稳时塌落土体的滑移角，将三维楔形体模型中上部棱柱体改为棱台体，如图4 所示。

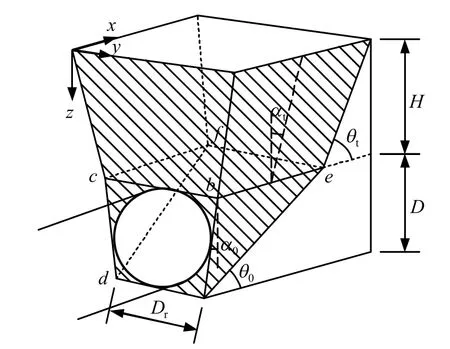
图4 M-M 模型Fig.4 M-M model

该模型考虑了滑动楔块的分层影响，获得的计算表达式为

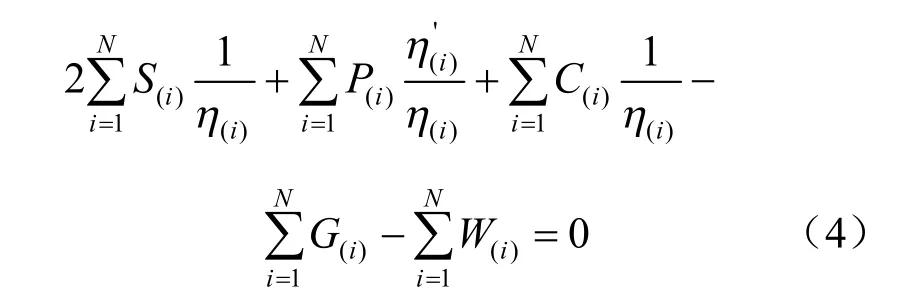
其中，η(i)=sinθi-cosθitanφ(i),η(′i)=cosθi+sinθi,tanφ(i)式中各量含义如图5 所示。

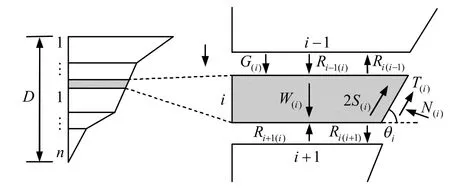
图5 滑动楔块第i 层单元受力的二维表示Fig.5 Two-dimensional representation of loading applied to ith layer of N-layer sliding wedge

同样地，根据地层土体类型将上部棱台体进行划分，再通过考虑滑动倾角的修正Terzaghi 公式进行每一段棱台体的竖向应力计算，即可迭代求得最终作用于开挖面楔块体上的竖向应力，如图6 所示。

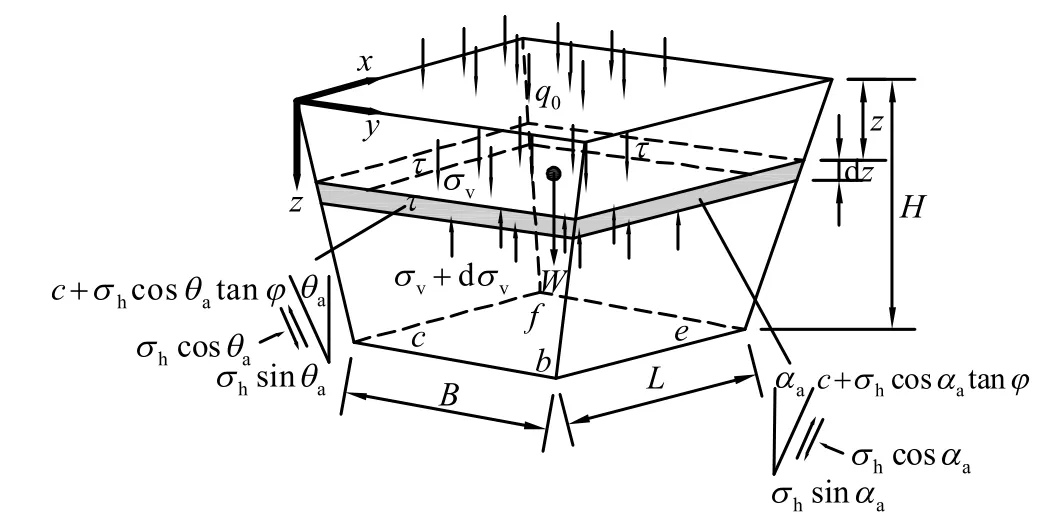
图6 竖向压力求解示意Fig.6 Solution of vertical stress

该模型通过试验和数值分析，滑移角可取α=π/4+φ/2以确定开挖面最小的支护压力Pcr。此外，M-M 模型上部滑落土体为棱柱体，比较适合于均质和非均质的黏性土层。

2.3.3 圆台-转角模型

圆台-转角模型假定开挖面破坏体由M-I和M-II 两个模块组成（见图7）。在空间上坍塌区域整体近似为上方削平的圆锥形M-I 模块，下方区域类似转角，即M-II 模块与上方M-I 模块光滑连接。开挖面破坏由靠近隧道底部开始诱发，并逐渐延伸至地表，最终形成漏斗形坍塌。

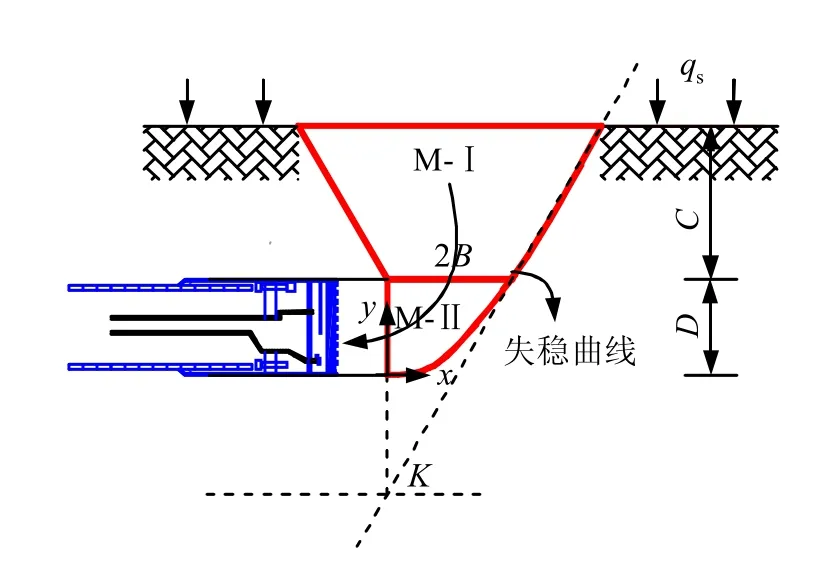
图7 圆台-转角失稳模型Fig.7 Round-elbow instability model

基于该模型得到的开挖面支护压力表达式为

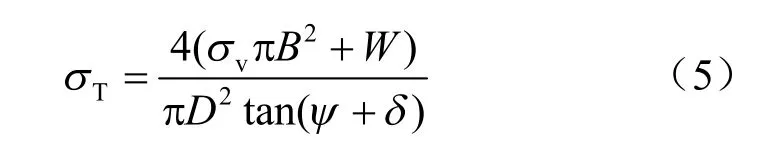
式中：ψ为考虑黏聚力后等效内摩擦角[14]；δ 取为N 与水平方向夹角；2B为松动区宽度，按2B=D/tan(π/8+φ/4)进行取值；σv为M-I 对M-II的竖向作用应力。

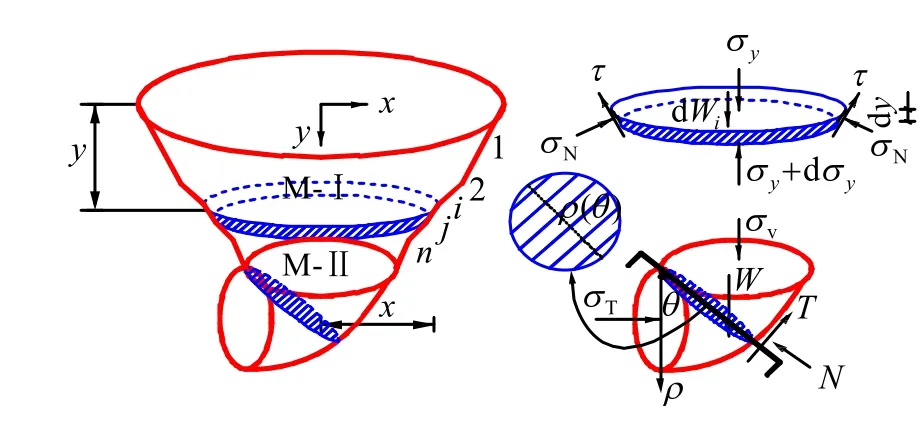
图8 圆台-转角模型极限受力分析Fig.8 Limit equilibrium analysis for round-elbow model

此外，该模型对于竖向应力σv的求解同样采用分层迭代的方法，如图8 所示。对于第i 层土体，单元体内的竖向应力可表示为

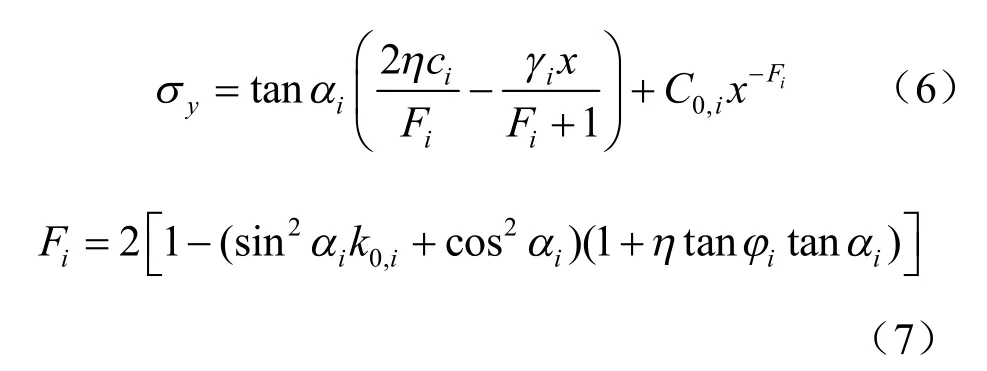
式中：C0,i由该单元体受力边界条件确定；αi、ci、φi、 γi、k0,i分别为第i 层土体的滑移角、黏聚力、内摩擦角、重度及水平侧压力系数；η为滑移面上土体的侧摩擦力利用程度系数，取1 表示下滑破坏，取-1 表示冒顶破坏。

3 软土地层开挖面支护压力可视化计算与分析

针对软土复合地层的特点，基于上述所建立的理论模型，为便于计算和分析，本文将TBM 开挖面临界支护压力的计算进行了可视化分析，并偏安全地采用了水土分算的方式进行计算。

3.1 可视化软件功能介绍

通过计算机编程，实现了基于C#.NET 的可视化计算程序(TBM Studio)。程序的主要功能包括：

（1）土体计算参数及施工参数的窗口交互；

（2）地层分布信息的交互及可视化表现；

（3）开挖面极限支护压力的多方法快捷计算；

（4）地层信息、施工参数、计算结果等文件的计算机本地存储和读写。

3.2 计算参数输入

需要输入的参数主要包括施工区段各地层的计算参数及分布信息。

（1）地层的计算参数

地层计算参数包括地层标识ID、土体总重度γ、有效黏聚力c′、有效内摩擦角φ′、静止土压力系数K0及可视化表现颜色Color 组成。所有地层计算可在图9 所示窗口中实现数据的快速编辑。

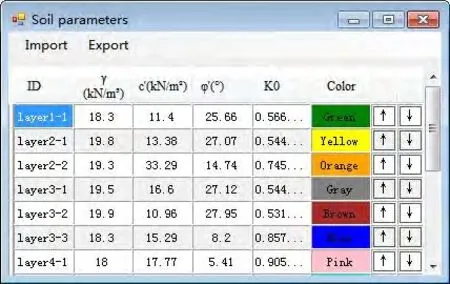
图9 地层计算参数展示窗口Fig.9 Display window of soil parameters

（2）地层分布信息

地层的分布信息可根据施工图纸中获得。具体计算时可将施工区间按照地勘钻孔位置分为多个断面，并逐一获得各界面的掘进里程坐标、地表标高、盾构埋深及各地层埋深等相关信息。

复合地层各断面的信息可由图10 所示窗口实现便捷编辑。

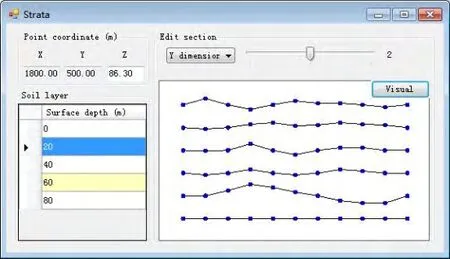
图10 地层信息编辑窗口Fig.10 Strata edit window

（3）施工及模型相关计算参数

盾构直径、地表超载、水位线标高、圆台-转角计算模型中土体摩擦利用程度参数η 以及M-M 计算模型中的楔底宽度Dr等在内的相关模型参数可在图11 所示的计算窗口输入。

3.3 可视化计算

可视化计算窗口的断面列表中列出了相关施工区段的所有断面。通过点击操作，可对所选断面的地层信息进行可视化表现，如图11 所示。

开挖面临界支护压力的计算以各断面为单元个体进行，相关计算参数也可根据需求作临时调整，最终结果为队列中所有已选断面计算结果的汇总。

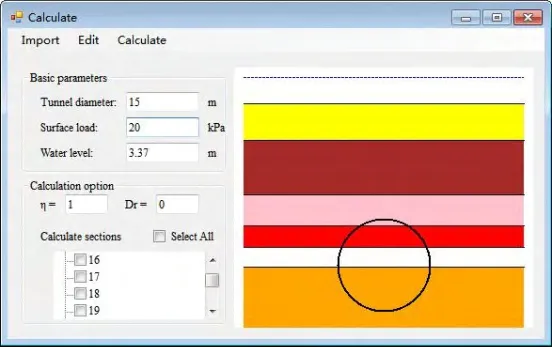
图11 可视化计算窗口Fig.11 Visual calculation window

3.4 结果输出

计算结果以断面标识、掘进里程坐标、各计算模型对应结果的形式输出到文本文件中。此外，记录文件可与Excel 实现交互，便捷地实现图表的制作。

4 工程实例分析

为了验证本文所建立模型的可靠性和进行对比分析，这里给出了作者参与的两个工程实例的计算结果。

4.1 实例1：Alaskan Way 隧道

（1）工程概况

Alaskan Way Viaduct Replacement Tunnel 是美国在建的一条连接西雅图南区（SoDo）和南湖联合区（South Lake Union）的17.3 m 大直径隧道，上下层双车道布局，采用日本生产的EPB 盾构，是目前世界上最大的土压平衡盾构隧道。隧道全长3.2 km（2 英里），工程投资42.5 亿美元，用于替换20 世纪50年代修建的高架路，由于经过多次地震后该高架路已不再适合继续使用。同时该隧道的建成能承担附近安全性能不再满足要求的Battery Street Tunnel 的交通流量，因此，对改善交通具有十分重要的意义。该工程于2013年下半年动工，预计2016年上半年竣工，隧道整体布局如图12 所示。

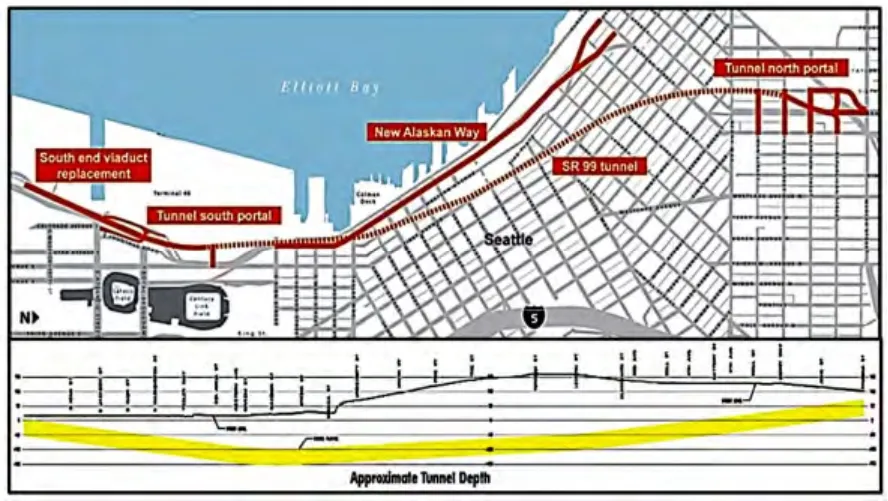
图12 Alaskan Way Tunnel 平面布局及纵向埋深分布Fig.12 Plan layout and vertical distribution for Alaskan Way Tunnel

该隧道为超大断面开挖面，要穿越典型的复合地层，主要特点为：

①隧道直径大达17.3 m，为目前世界上最大的土压平衡盾构隧道。由此开挖面拱顶和底部存在巨大压力差值，同时开挖面同时穿越多层性质差异较明显的地层，开挖面稳定性较中小隧道复杂。隧道全长3.2 km（2 英里），掘进距离长，加上其经受多次冰川作用的影响，纵向地层变异性比较明显，在掘进过程中需考虑由此产生的影响。

② 根据工程地勘报告，西雅图地区至少受到多达6 次严重的冰川作用，而隧道所在轴线处穿越地层主要为冰川作用后的冰碛土，目前没有关于这方面的盾构经验，具有非常大的工程挑战性，Alaskan Way Tunnel 工程的掘进将填补此类工程的空缺。

③影响隧道开挖面稳定的另一主要因素为该隧道靠近艾略特湾（Elliott bay），地下水水头高，超出地表达1 m 左右。工程中在确定盾构土舱压力参数时，由于隧道横断面地层差异明显，渗透系数差异较大，而水、土分算和水、土合算确定的设计值差异巨大，因此，成为影响工程抉择的一项难题。

④ 隧道覆土厚度较浅，为22.3 m，仅为隧道直径的1.3 倍左右，因此，对周边环境影响控制成为工程中关注的另一个重要焦点。而且由于该隧道在原有高架路下面施工，地表车流密度较大，更给工程带来严峻挑战。

（2）开挖面支护压力计算

根据项目地勘资料，各地层的计算参数选取如表1 所示。

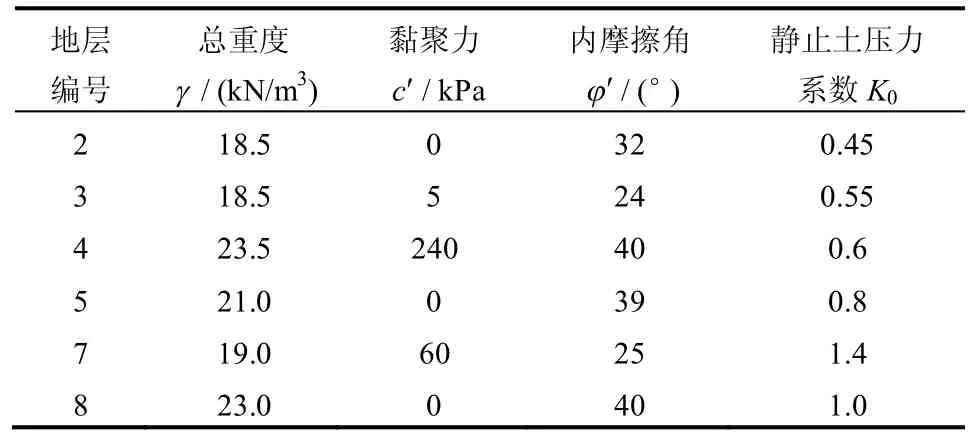
表1 阿拉斯加隧道穿越地层土体参数Table 1 Geotechnical parameters for Alaskan way tunnel

通过可视化计算程序得到的该隧道在3 种方法下的临界支护压力值如图13 所示。

（3）结果分析

①下限解对比分析

3 种模型对应的下限解较为接近。其中，用圆台-转角模型计算得到的支护压力下限解最大，三维楔形体模型次之，而M-M 模型得到的下限解最小。

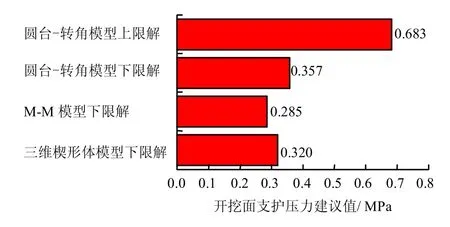
图13 不同方法计算结果比较Fig.13 Comparison among calculated results by different methods

本实例穿越的地层中，编号为4、7 的两层土的黏聚力及内摩擦角都较大，而隧道开挖面前近一半的土体都属于这两个地层，其本身的自稳性较好。

M-M 模型考虑了隧道掘进前方滑动楔块的分层效应，较为充分地考虑了4、7 地层的自稳性，因此，得到了较小的临界支护压力下限值；其他两种算法则通过按地层厚度加权将开挖面前土体均一化处理，在一定程度上折减了土体的力学强度，没有充分考虑地层的自稳性，得到了较大的临界支护压力下限值。

② 圆台-转角模型上、下限解分析

按照圆台-转角模型得到的支护压力上、下限解之比约为2，反映了较大的安全支护压力跨度范围。

根据该模型的假定，在上、下限解的求解中，滑动面侧摩阻力分别发挥增加、减小上部覆土重量的作用。造成上、下限解跨度较大的原因也可以归结为穿越的地层具有较好的自稳性。

4.2 实例2：钱江隧道

（1）工程背景

钱江隧道位于著名的观潮胜地海宁盐官镇上游约2.5 km 处，北岸位于嘉兴海宁市盐官镇，南岸位于杭州市萧山区，隧道与钱塘江河道呈垂直相交，隧道外径为15.43 m，全长4.45 km。

钱江隧道场地位于浙北平原区，为钱塘江河口冲海（湖）积平原地貌，根据沉积环境、软土与粉土分布、土层层序特征，钱塘江过江隧道沿线可细划为江北岸海积平原区、钱塘江河床区及江南岸冲海积平原区3个沉积地貌单元。整个隧道穿越的地层分布如图14 所示。

钱江隧道工程地下水主要体现为潜水和承压水，其中潜水主要赋存于沿线浅部人工填土及江中、江南浅部的粉、砂性土层内，地下水分布连续，其富水性和透水性具有各向异性，特别是钱塘江两岸的地表填土层，透水性良好，下部粉性土层透水性弱。

图14 钱江隧道三维地层图Fig.14 Three dimensional profile of strata around Qianjiang tunnel

（2）开挖面支护压力计算

钱江隧道穿越各地层物理力学参数指标如表2所示。

刀盘主要穿越的地层为4-1、4-2、5-2、5-3 及5-4 粉质黏性土，自稳性较差。

根据施工图纸将施工区段各断面地层信息综合分析，地表超载取为20 kPa，可得全区段极限支护压力下限值（塌落）结果如图15 所示。

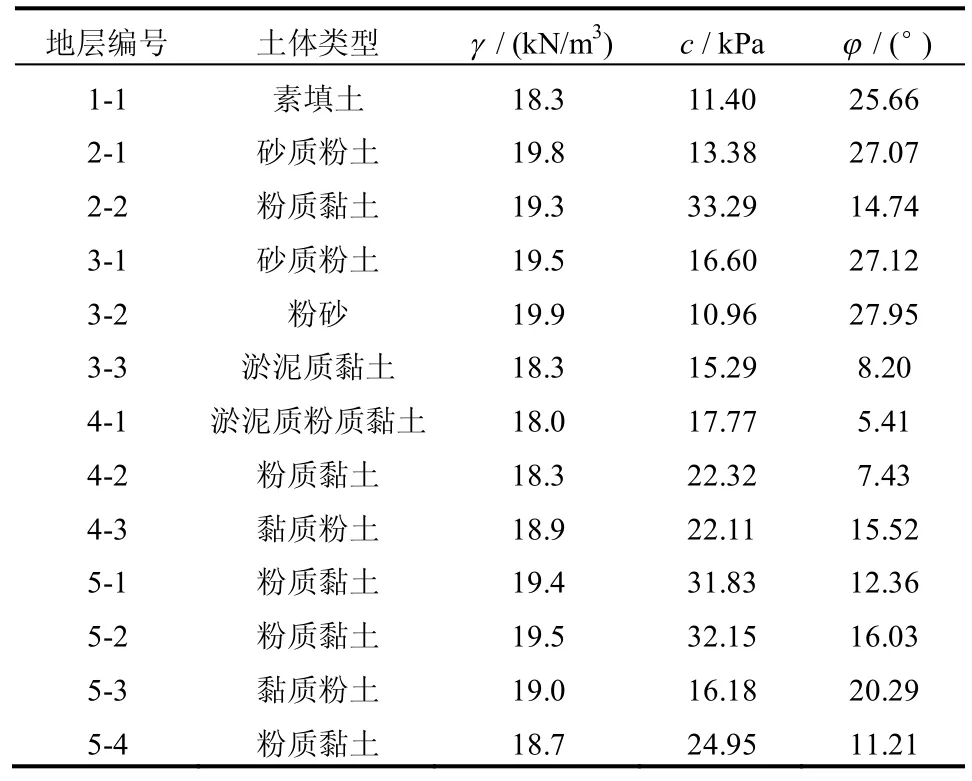
表2 钱江隧道穿越地层物理力学参数Table 2 Physical and mechanical parameters of strata crossed by Qianjiang tunnel

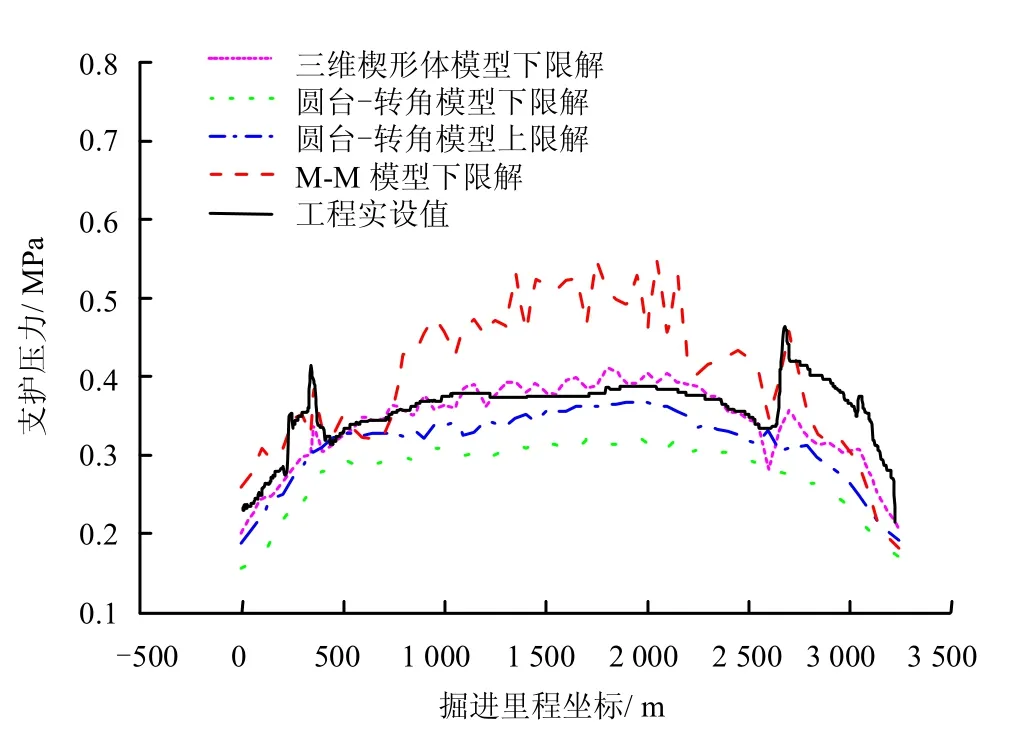
图15 不同方法计算结果Fig.15 Results of different methods

（3）结果分析

①根据工程实测地表沉降数据，在江岸施工段上，大部分测点均为隆起状态，即工程实设支护压力偏保守。本实例中，三维楔形体模型的计算结果与工程实设值以及区段上的静水压力都较接近。反映出土体有效应力低，对滑动楔块上竖向作用力的贡献较小。

② 采用M-M 模型得到的支护压力下限解高于工程实设值，较为安全。造成这种结果的主要是因为盾构除在江南岸区段有3-2 粉砂土层穿越外，刀盘面主要穿越地层为4-1、4-2、5-2、5-3 及5-4 粉质黏性土，地层土体的自稳性相对较差。滑动楔块的分层偏保守地考虑了这一不利因素，致使支护压力的下限解值明显高于其他两种方法。

③采用圆台-转角模型得到的上、下限解均低于工程实设值。说明模型的假定或参数的选取仍需根据工程复合地层情况进行调整。

5 结 论

（1）改进的三维楔形体模型的支护压力下限解受地层自稳性影响较小，结果相对稳定、保守。

（2）M-M 模型受地层自稳性的影响较大。在土体力学参数较好的地层中，该方法能充分地发挥土体的自稳性，使得到的结果偏小；在自稳性较差的地层中，则偏保守地考虑了过多的上部覆土，造成相对安全的结果。进一步可以考虑按地层特性及覆土深度对上部棱台体尺寸进行适当修正，以使M-M模型能够更为广泛地应用到开挖面支护压力计算中。

（3）圆台-转角模型受地层自稳性影响也比较明显，充分考虑了复合地层的成层及不同土体特性。但在土体力学参数较好的地层中尚缺乏对地层自稳性的充分利用，且在力学参数较差的地层中还需有效地分析上部覆土的竖向作用力影响。此外，还可考虑对上部圆台体的受力特性进行改进，以提高该模型在不同地层条件下的适用性。

本文所建立的3 种模型各有优缺点，相信随着计算模型及方法的不断改进，可视化程序将会能更加有效地确定出适合实际工程的开挖面支护压力计算模型，并为工程实践提供更加实用、有价值的指导。

[1]DAVIS E H,GUNN M J,MAIR R J,et al.The stability of shallow tunnels and underground openings in cohesive material[J].Géotechnique,1980,30(4):397-416.

[2]李昀.软土中超大直径泥水平衡盾构开挖面稳定性研究[D].上海:同济大学,2008.LI Yun.Stability analysis of large slurry shield-driven tunnel in soft clay[D].Shanghai:Tongji University,2008

[3]HORN M.Horizontaler erddruck auf senkrechte abschlussflǎchen von tunneln[M].Budapest:Landeskonferenz der ungarischen Tiefbauindustrie,1961:7-16.

[4]LECA E,DORMIEUX L.Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material[J].Géotechnique,1990,40(4):581-606.

[5]HU Xin-yu,ZHANG Zi-xin,KIEFFER S.A real-life stability model for a large shield-driven tunnel inheterogeneous soft soils[J].Front.Struct.Civ.Eng.,2012,2:176-187.

[6]张子新,胡文.黏性土地层中盾构隧道开挖面支护压力计算方法探讨[J].岩石力学与工程学报,2014,3:606-614.ZHANG Zi-xin,HU Wen.Investigation on excavation face support pressure calculation methods of shield tunnelling in clayey soil[J].Chinese Journal of Rock Mechanics and Engineering,2014,3:606-614.

[7]胡文.复杂地层中大直径泥水盾构开挖面支护压力计算理论及工程应用研究[D].上海:同济大学,2014.Hu Wen.Study on face pressure calculation theory and engineering application of large-diameter slurry shield tunnelling in complicated geological strata[D].Shanghai:Tongji University,2014

[8]JANCSECZ S,STEINER W.Face support for a large mix-shield in heterogeneous ground conditions[J].Tunnelling,1994,94:531-550.

[9]ANAGNOSTOU G,KOVÁRI K.Face stability in slurry and EPB shield tunneling[C]//Proceedings of Geotechnical Aspects of Underground Construction in Soft Ground.Rotterdam:Balkema,1996:453-458.

[10]ANAGNOSTOU G,KOVÁRI K.The face stability of slurry-shield-driven tunnels[J].Tunnelling and Underground Space Technology,1994,9(2):165-174.

[11]ANAGNOSTOU G,KOVÁRI K.Face stability conditions with earth-pressure-balanced shields[J].Tunnelling and Underground Space Technology,1996,11(2):165-173.

[12]BROERE W.Tunnel face stability and new CPT applications[D].Netherlands:Delft University,2001.

[13]JANSSEN H A.Versuche über Getreidedruck in Silozellen[J].Zeitschrift des Vereins deutscher Ingenieure,1895,XXXIX(35):1045-1049.

[14]李恒太,郭秀兰,周立峰,等.等效内摩擦角的计算与使用[J].岩土工程界,2001,(8):34-35.LI Heng-tai,GUO Xiu-lan,ZHOU Li-feng,et al.Calculation and application of equivalent internal friction angle[J].Geotechnical Engineering World,2001,(8):34-35.

[15]LI Y,EMERALD F,KASTLER R,et al.Stability analysis of large slurry shield-driven tunnel in soft clay[J].Tunnelling and Underground Space Technology,2009,24(4):472-481.