考虑饱和土的地铁车站结构非线性地震反应研究
2015-02-15庄舒曼卓卫东
谷 音,庄舒曼,卓卫东,孙 颖
(福州大学 土木工程学院,福建 福州 350116)
1 引 言
阪神地震导致地铁车站的破坏引起了学者对地下结构抗震的重视。随着地下空间开发利用日益增加,近年来学者对考虑软土地基条件下的地下结构抗震方面进行了广泛研究,在有限元与无限元混合方法以及人工边界、软土本构等研究中获得了许多成果[1-6]。饱和土在自然界中广泛存在,我国南方含水丰富地区软土地基条件下大量修建地铁等地下结构,考虑饱和土两相介质性能更接近实际地质条件。文献[7]研究表明,饱和土体和弹性土体的位移响应具有明显区别,因此,应考虑饱和土性质对结构的影响。
广泛存在于自然界的饱和土层可以简化为两相多孔介质的物理模型进行分析,流体饱和多孔介质波动问题涉及的波动方程为固-液耦合的二阶偏微分方程组。基于饱和多孔介质动力响应的复杂性,理论研究主要局限在简单边界情况以及数值求解方法,考虑饱和地基地下结构动力反应的数值研究主要集中在频域及弹性分析。Prevost 等[8]提出了用于土坝弹塑性地震反应分析的二维有限元数值计算方法,土层可以考虑多层的饱和多孔介质的情况,土骨架按照非线性进行处理。赵成刚等[9-10]提出了用时域显式有限元方法来求解流体饱和两相多孔介质动力方程,研究了饱和无黏性土沉积层表面的无质量刚性基础的动力反应,提出了惯性质量耦合项影响下的流体饱和两相多孔介质动力反应计算分析的时域显式有限元方法,分析了两相介质中固相和液相动位移在惯性质量耦合项下的影响。杜修力等[11]在进行流体饱和两相多孔介质动力问题计算分析时采用了一种新的时域显式逐步积分格式。赵江倩等[12]建立和求解饱和土中圆形隧道在地震加速度作用下的动力控制方程,张鸿等[13]基于Biot 理论分析了地震P 波作用下饱和土体重圆形隧洞衬砌的动力响应问题,采用波函数展开法求解饱和土体重的散射波场。
考虑饱和介质的数值方法用于解决较为复杂的问题时,由于自由度计算量大,占用内存及时间消耗较大,处理非线性问题遇到困难,限制了上述方法的应用。为克服这些缺点,引入了等效黏弹性人工边界单元,提出考虑饱和土层的人工边界和饱和土非线性的有限元分析方法,将结构周围的土体视为固-液二相介质,建立了饱和土-结构动力相互作用模型,对地下结构地震非线性反应进行数值模拟,对比了数值方法中考虑饱和土和单相土时的情况,并与振动台试验数据进行对比,通过数值参数分析,研究了饱和土-地下结构动力非线性性能。
2 饱和土-结构有限元时域数值模型
2.1 饱和土介质的等效人工边界单元
对于复杂的几何形状以及考虑近场区域介质的非均匀和非线性时,分析无限或半无限空间的时域动力问题通常采用有限元模型的数值方法进行分析,此时采用的有限域为了反映无约束域能量辐射效应影响,需引入虚拟的人工边界条件。刘光磊等[14]、王子辉等[15]研究了饱和无限地基的数值模拟的人工边界问题,为时域分析饱和土-结构的动力相互作用提供了基础。对于常见的实际工程而言,散射波场的假定较平面波的假定相比更符合实际情况,由其构造出的边界不仅能较好地模拟地基的辐射阻尼,而且也能模拟原场介质的弹性恢复能力,具有很好的低频稳定性。
Zienkiewicz 的研究表明,一般情况下如中等速度运动时,可以忽略流体加速度,此假定适用于包括地震工程在内的大部分中低振动频率的工程问题[14]。以此假定为基础,针对柱面压缩波从径向为0 的位置向四周传播,基本控制方程可写成含有未知量u和p 的形式:
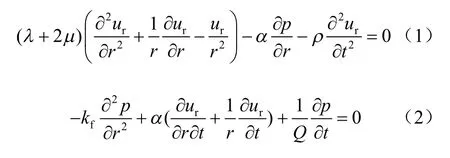
式中:u为位移;p为孔隙水压;λ 与μ为土骨架的拉梅常数;ρ为密度;和分别为对径向位移的二次和一次微分,和为对时间的二次和一次微分;kf为动力渗透系数;α、Q为与固体和流体的压缩性相关的系数:α=1-Kb/Ks,1/Q=(α-n)/Ks+n /Kf,n为孔隙度,Ks、Kf和Kb分别为土颗粒、流体和土骨架的体积模量。
根据文献[14],在渗透性较低的情况下可先假设渗透系数为0,从而求解得到边界上各量之间的关系。在推导流量边界条件时则采用真实的渗透系数,求解上述方程可得边界满足以下关系:
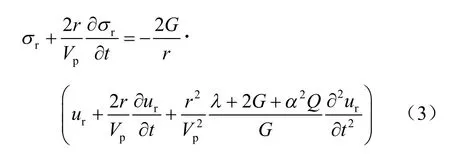
式(3)即为二维黏弹性传输边界在法向的边界方程。选用适当的元件参数,可使与元件系统相连的边界微元面上的正应力与该处位移、速度等量之间满足式(3)的关系。根据文献[16],可采用与实体单元替换弹簧-阻尼单元体系,即在边界上沿边界面法向延伸一层厚度相等的实体单元,并将外层边界固定。则其等效剪切模量、弹性模量和等效单元的阻尼系数分别:
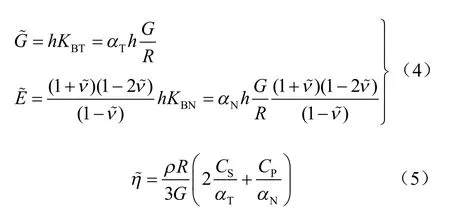

式中:qr为流量;为径向加速度。
2.2 地震输入及分析方法
波动输入通过在人工边界单元的节点上施加等效荷载,使其作用下节点位移和应力分别与原波场相同。采用软件编制辅助计算程序获得模型中自由波场的人工边界节点位移和应力值,根据文献[16],可按照式(7)计算人工边界单元内节点上施加的等效节点荷载,计算流程如图1 所示。
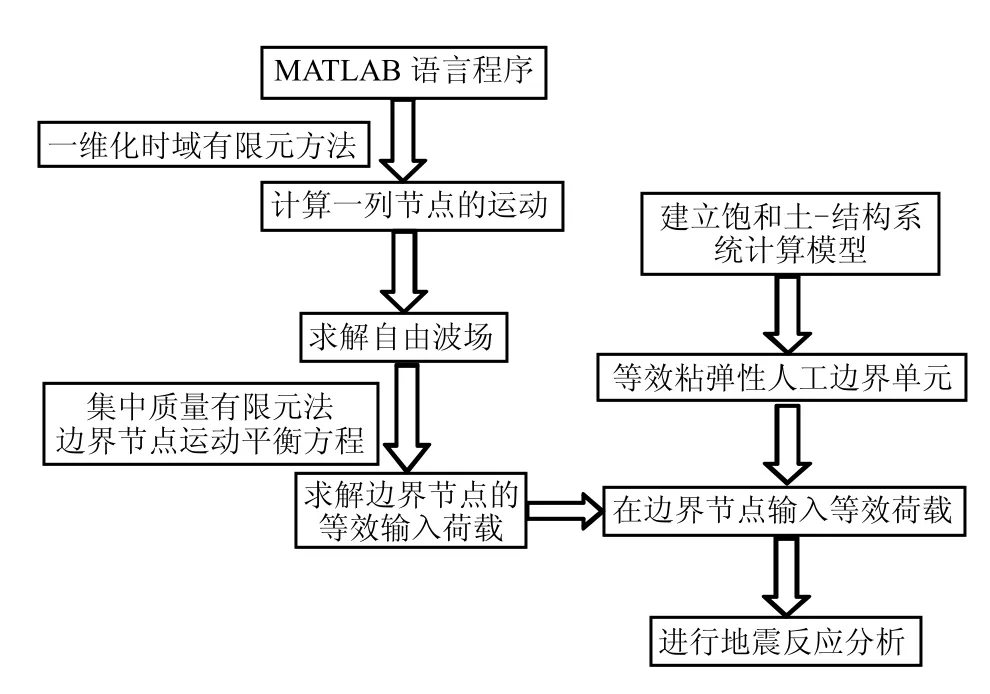
图1 地震波输入程序流程图Fig.1 Program flow chart of inputting earthquake waves
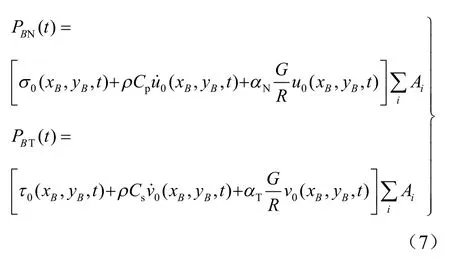
式中:下标BN为B 节点的法向边界;BT为B 节点的切向边界;PBN(t)和PBT(t)分别表示法向和切向人工边界节点B 上在t 时刻施加的等效荷载,其中xB,yB是人工边界节点坐标;τ0为切向应力;为法向位移;为切向位移。
2.3 材料本构模型
饱和多孔介质的动力反应特性基本呈现出弹塑性性质[10],根据模拟的黏土材料性质,土体本构材料选用基于Biot 模型的u-p 形式的孔压独立弹塑性材料,如图2 所示。该材料适用于模拟对于材料的剪切性能约束改变较为敏感的单调或者循环反应,塑性仅在偏离应力-应变响应时出现,曲线公式及具体参数取值参见参考文献[17]。
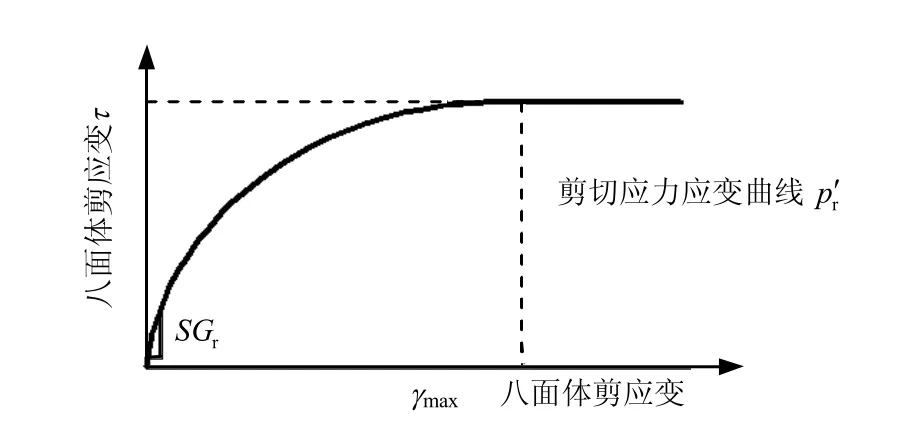
图2 土材料应力-应变曲线Fig.2 Stress-strain curve of soil
混凝土柱采用纤维截面单元考虑其非线性动力性能。约束混凝土采用Scott 修正的Kent-Park 混凝土计算模型,即在Kent-Park 模型的基础上通过改变混凝土受压骨架曲线的峰值应力、峰值应软化阶段的斜率来达到横向箍筋的约束效果,其应力-应变关系曲线如图3(a)所示[17-19]。钢筋采用经过Filippou修正后的 Menegotto-Pinto 本构计算模型[19],Menegotto-Pinto 本构模型如图3(b)所示,其中σ为应力,ε为应变,E为弹性模量,具体参数取值参考文献[19]。
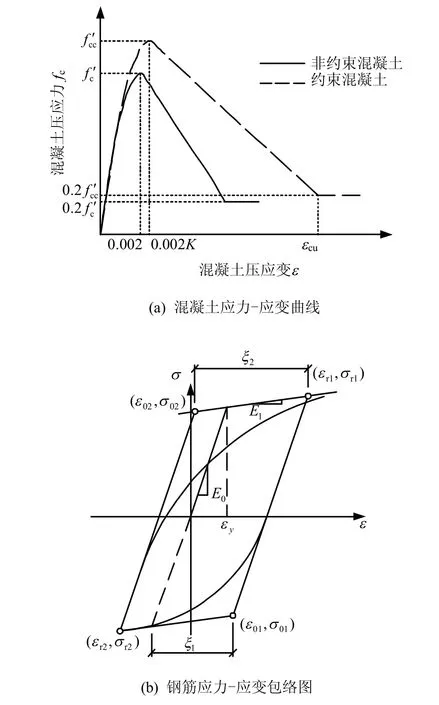
图3 钢筋混凝土结构本构模型Fig.3 Constitutive models of reinforced concrete structure
3 饱和土-地铁车站地震反应分析
3.1 有限元模型
以地铁某饱和黏土地基条件下的双柱三跨地下两层车站为工程背景,地下一层为站厅层,地下二层为站台层。车站主体为整体结构,中间内设框架柱。车站主体结构长为172 m,宽为23.8 m,高为13.46 m。顶板厚0.8 m,中板厚0.4 m,底板厚0.9 m,中柱截面边长尺寸为1 m,站台中心处埋深约15.86 m。车站结构横截面图如图4 所示。
基于Opensees 平台建立了饱和土-结构整体有限元模型,如图5 所示,模型尺寸为50 m×100 m。根据所在地质的黏土特性,采用了2.3 节介绍的基于u-p 考虑孔压独立的多相弹塑性材料模拟饱和两相介质模型。单元设置为2 m×2 m 的平面四边形流-固耦合单元。在土体底部及左右边界都施加了等效黏弹性人工边界单元,参数根据式(4)~(6)进行计算,根据单元特性,边界设置为不排水条件,自由面表面为排水条件。梁材料为C35 混凝土,柱采用C40 混凝土,梁和柱采用纤维截面的非线性梁柱单元进行离散,各材料本构如图2、3 所示。车站所在土体为单层饱和土,上覆土层厚5 m,根据实测得到物理参数见表1。含水率大于60%时,按照饱和土考虑。根据文献[21],取不考虑滑移和脱开时更不利的情况进行分析。
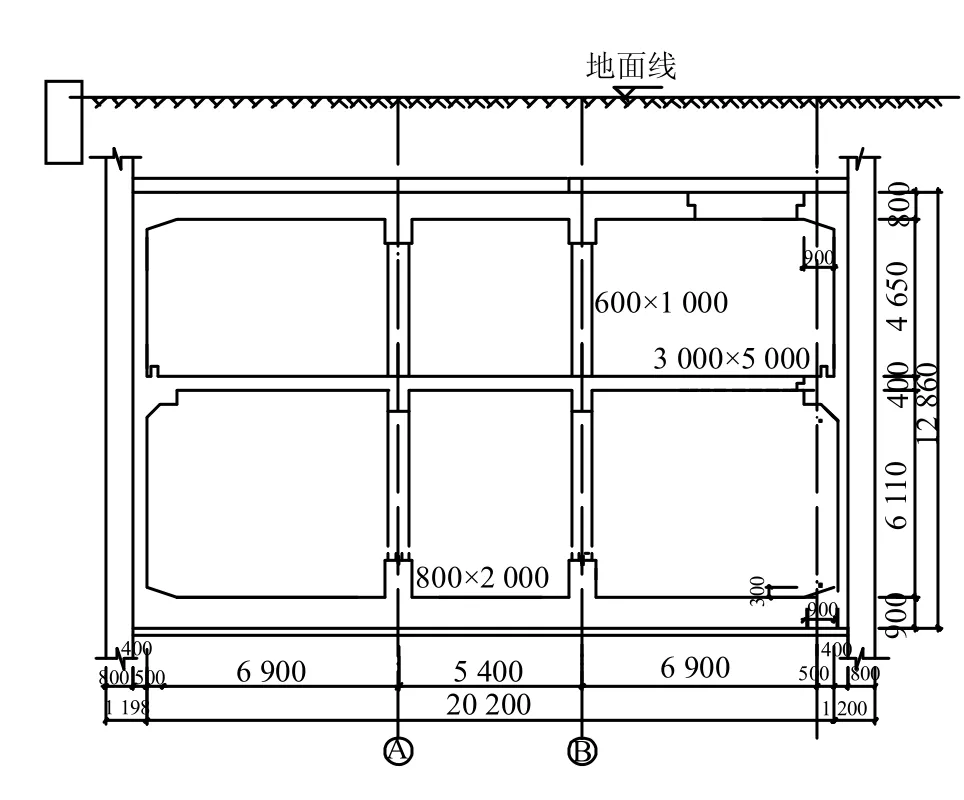
图4 车站结构横截面图(单位:mm)Fig.4 Cross-section of subway station(unit:mm)
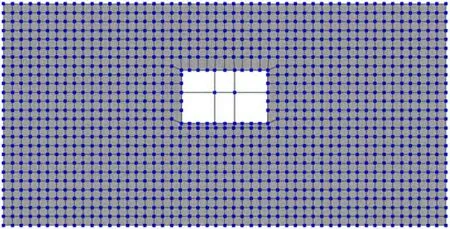
图5 饱和土-车站整体有限元模型Fig.5 Finite element model of saturated soil-station system

表1 土层物理特性Table 1 Soil parameters
3.2 人工边界单元精度验证
取与表1 同样参数,建立单元尺寸为1 m×1 m的大小为10 m×10 m范围的土层验证等效边界单元的精度,如图6(a)所示,其中o、a和b为观测点。边界单元的参数按照式(4)~(6)计算。施加冲击荷载及观测点如图6(b)所示。
图7 显示了二维问题中地表受冲击荷载作用时,用黏弹性边界、扩展解和固定边界分别计算的结果。从结果可以看出,黏弹性边界较好的模拟约束土能量的辐射作用,计算结果与扩展解十分接近。
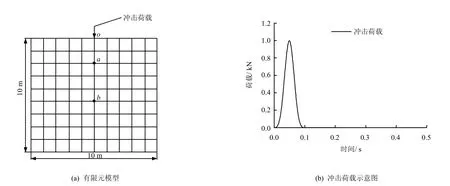
图6 验证算例Fig.6 Verify example
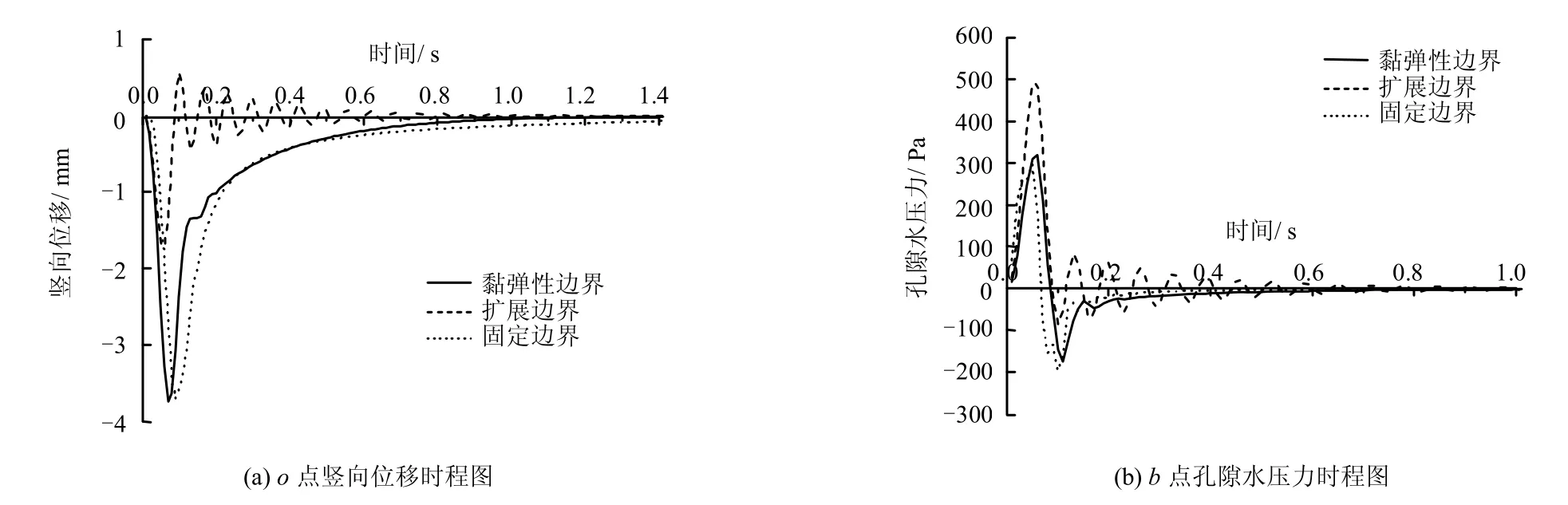
图7 观测点时程图Fig.7 Time history curves of different points
3.3 地震波输入
根据工程所在场地类别为Ⅳ类,选取了Ⅳ类场地条件下不同频谱的Kobe 地震波和Elcentro 波进行地震响应分析。调整为峰值为0.1 g 的加速度及其相应位移-时程曲线分别如图8 所示。
3.4 数值计算与振动台模型试验结果对比
采用钢箱、原型土、镀锌钢丝和微粒混凝土制作小比例尺模型与数值方法相互验证。为了消除箱壁钢板的边界效应,文献[22]对钢箱边界效应进行了研究。根据相似理论的要求及振动台设备承载能力,确定模型与原型结构几何尺寸相似比为1/30,模型及应变布置见图9,其中S为上层柱应变片编号,X 表示下层柱应变片编号,Z为中柱编号,模型相似比及尺寸参数详见文献[23],加速度峰值相似比为7.5,应力为1/4,应变为1,位移比为1/30。对应实际车站峰值加速度为模型车站构件截面尺寸较小,为防止人工配重过程中对模型车站构件造成损伤,忽略重力相似率,直接采用弹性相似率。
由于重量限制,振动台加载最大峰值为0.5 g,根据相似比,对应实际地震波峰值加速度为0.067 g。振动台试验条件下采用小比例尺模型,存在包括重力失真、现有试验条件下高频成分被滤掉等问题,与数值模型结果比较时主要分析了二者结果是否具有相同的变化规律,将试验和数值结果放于同一图中,对比了数值分析采用饱和土、单相土及试验结果,其中左竖向坐标统一为车站相对高度,上横坐标为试验值,下横坐标为数值分析分别采用饱和单向土计算的结果。
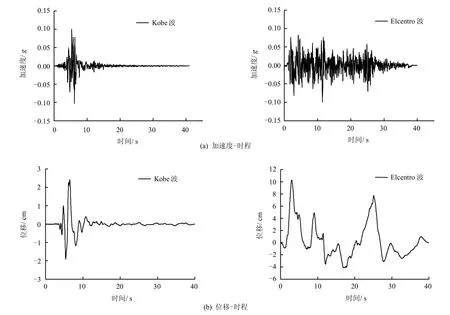
图8 输入地震波加速度与位移时程Fig.8 Time history waves of acceleration and velocity
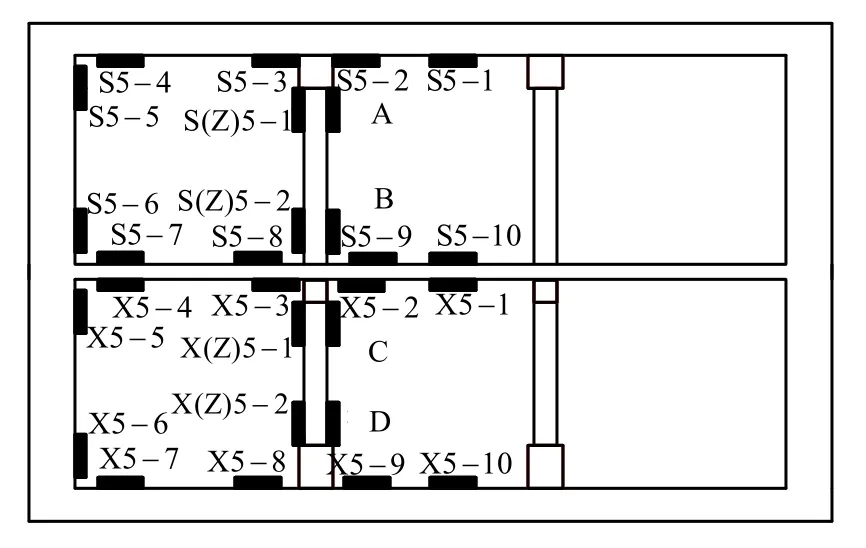
图9 应变片布置图Fig.9 Arrangement of strain foil
图10为地铁车站侧墙外部靠近结构底板、中板及顶板土压力峰值数值计算结果,试验值与数值解规律相似,都为中板土压力较大,底板以及顶板土压力相对较小,呈现中间大两头小的趋势。
图11为地铁车站侧墙外部靠近结构底板、中板及顶板加速度峰值结果。考虑饱和土情况下底板加速度最小,中板次之,顶板最大。
3.5 车站数值模型反应分析
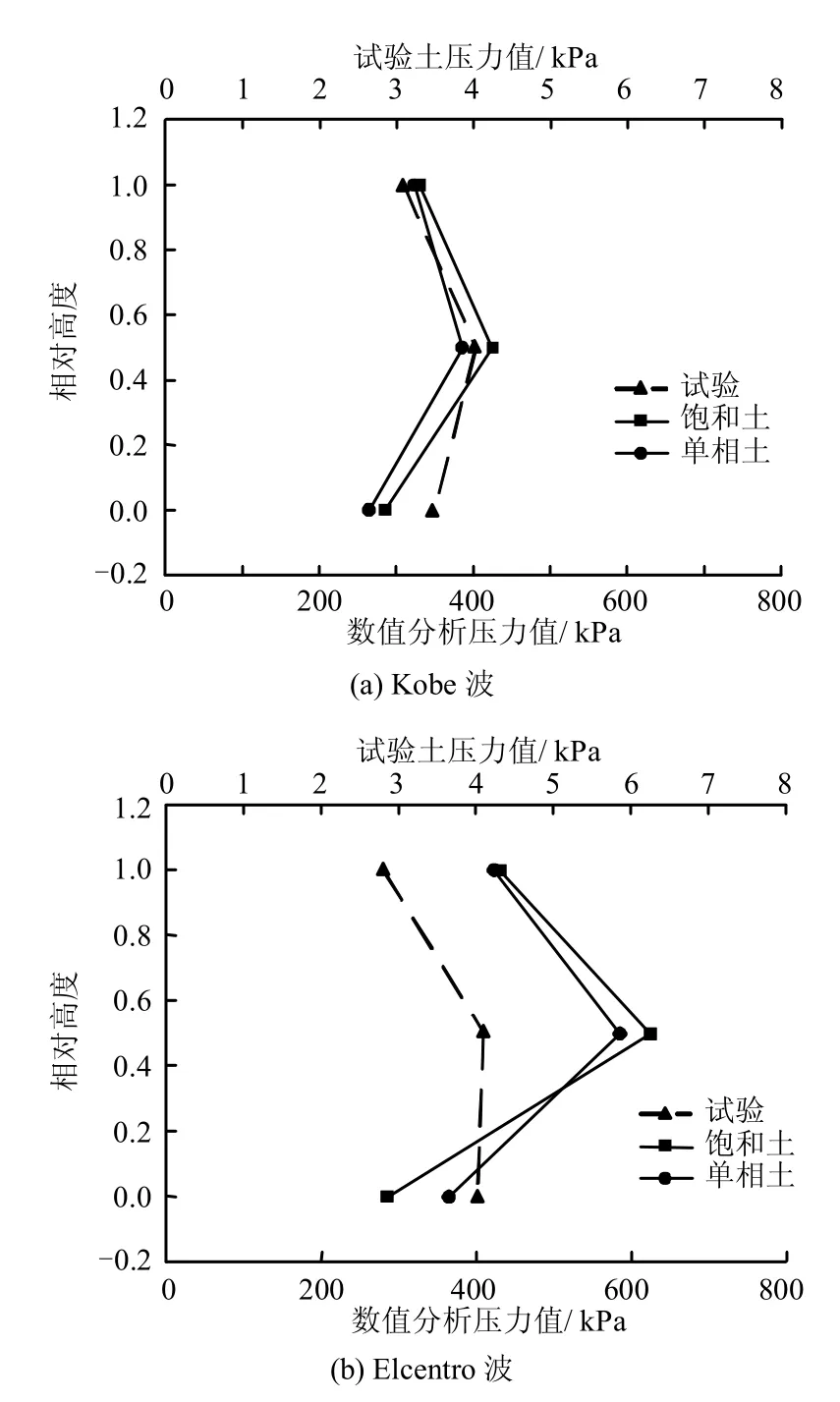
图10 土压力变化规律Fig.10 Variation law of soil pressure
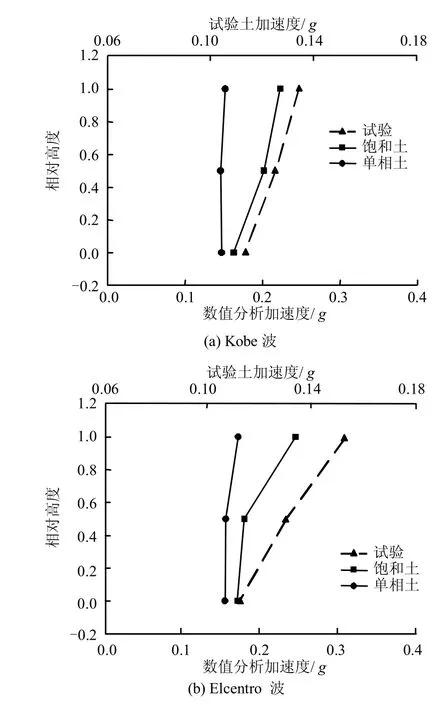
图11 加速度变化规律Fig.11 Variation law of acceleration
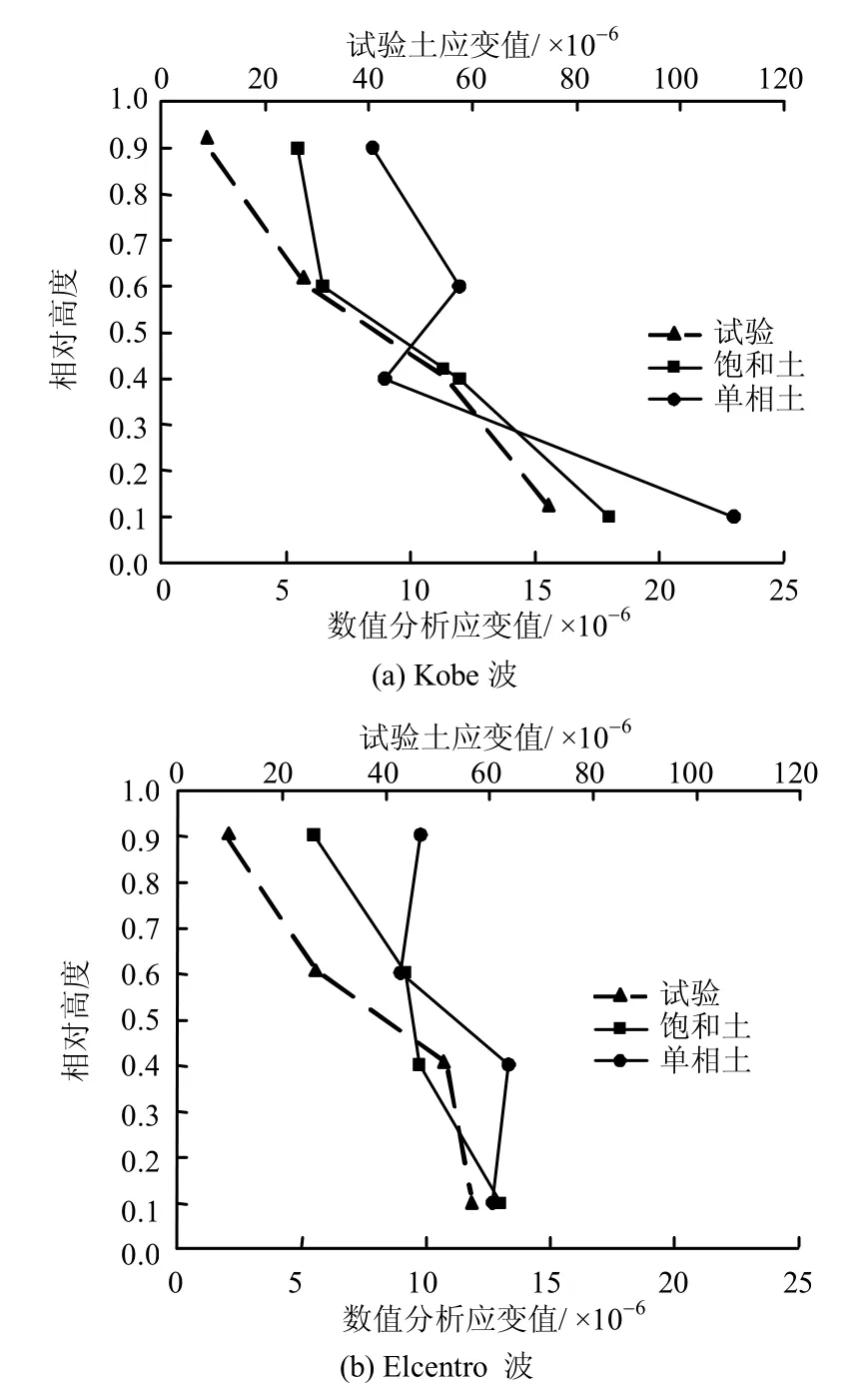
图12 中柱应变规律Fig.12 Strain of middle column
图12为结构中柱应变试验结果与数值模拟的比较。图中对应各点观测点从上至下依次为A,B,C和D,如图9 所示,分别为上层中柱柱顶和柱底,下层中柱柱顶和柱底。分析可以看出,考虑饱和土情况下计算所得应变较大,与试验所得结果更为接近。在横向地震过程中,结构各层会产生相对位移,层间位移较大会造成结构的破坏。图13 给出了地铁车站结构在横向地震作用下模型中柱在顶板、中板和下层底板位置的最大位移。表2为上、下两层中柱的层间位移,可以看出,Kobe 波作用下上层柱层间位移较大,考虑饱和土情况下所得的层间位移比简化为单相土时大,Elcentro 波作用下考虑饱和土的层间位移比单相土小。
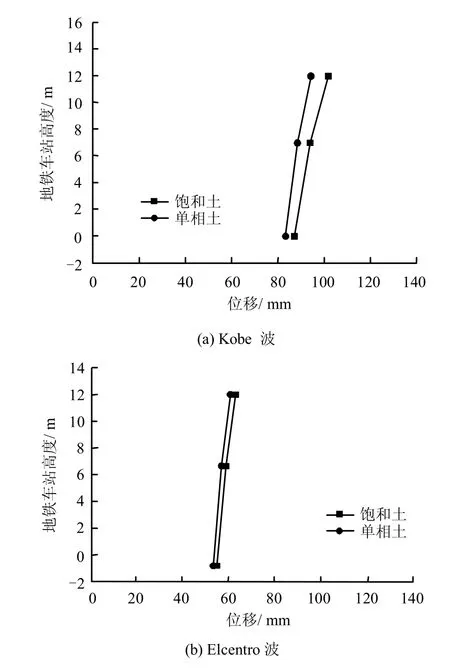
图13 车站位移时程图Fig.13 Time history curves of station displacement
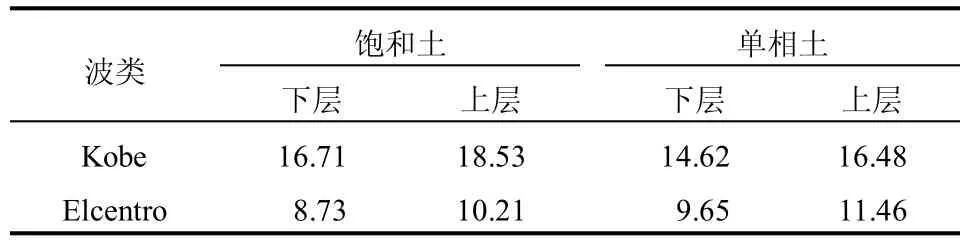
表2 各层层间位移最大值(单位:mm)Table 2 The maximum displacement between each layer(unit:mm)
在横向地震作用下,通常中柱两端所承受的弯矩最大。图14 比较了分别采用非线性饱和土单元和单相土情况下,不同地震波入射时中柱顶端最大弯矩时程图。可以看出,考虑饱和土情况下得到的柱端弯矩值与简化为单相土情况下计算所得的弯矩值大。
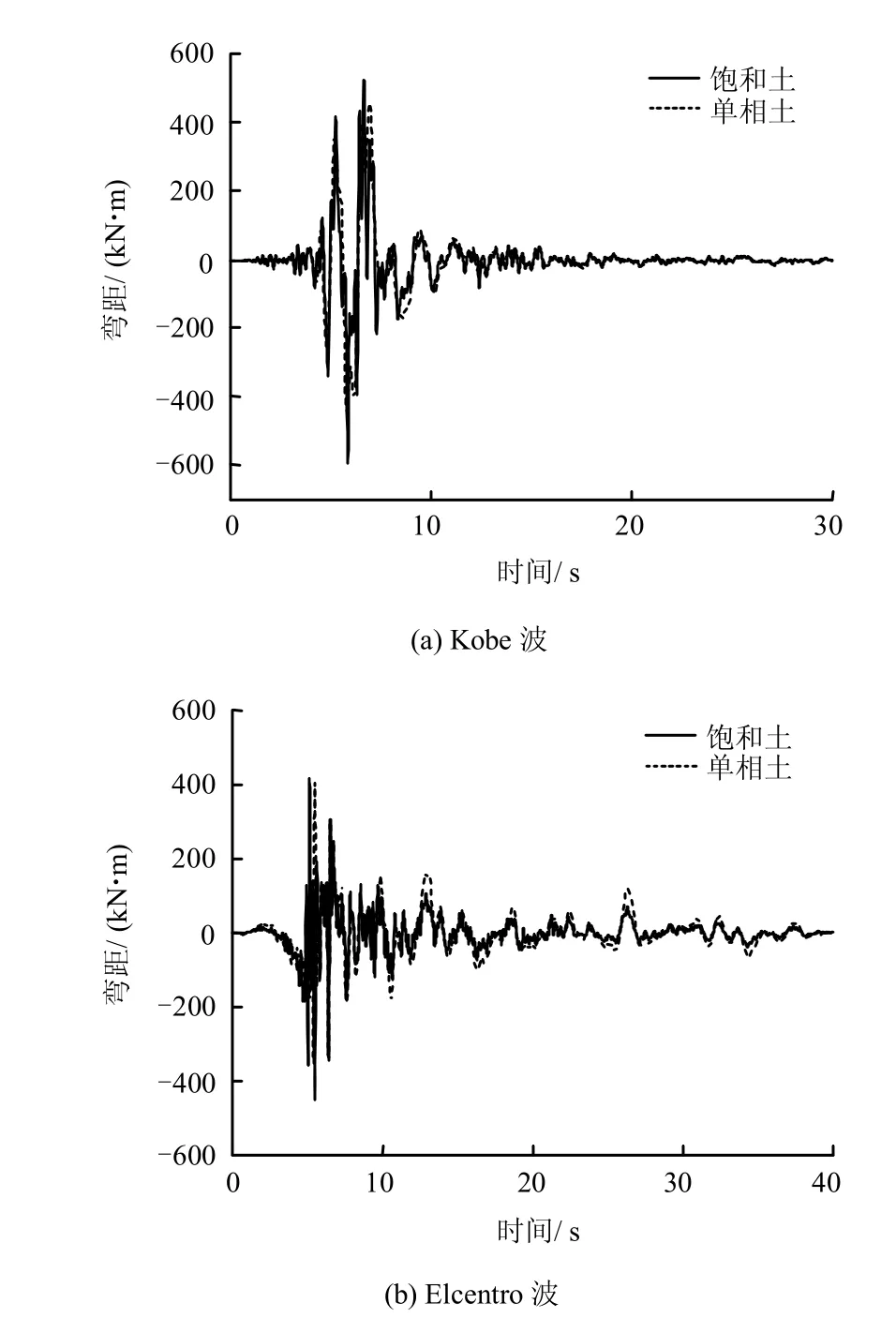
图14 上层中柱顶端弯矩Fig.14 Top moment of the middle column
4 结 论
(1)研究了考虑饱和土介质传播特性的等效黏弹性人工边界单元,并进行了数值验证,基于地震波转化为作用于人工边界节点上等效荷载的方法实现了波动输入。
(2)通过与地铁车站振动台试验结果进行对比,分别分析了考虑饱和土非线性性质和仅考虑单相介质情况下地铁车站的地震响应规律。在选取的两条不同地震波作用下,采用考虑多相介质的饱和土计算的结果与单相土的计算结果相似,与试验结果进行比较,具有相似的分布规律:沿着地铁车站结构高度方向上侧墙外部土压力分布成中间大两边小的趋势,顶板峰值加速度最大,底板最小,顶板侧向位移最大,中板次之,底板最小,顶层层间位移大于底层。在地震作用下,中柱所受到内力比较大。
(3)对数值分析结果的比较可以看出,简化为单相土计算所得的土压力、加速度、侧向位移以及结构内力普遍较考虑饱和土情况下计算所得结果偏小。与单相固体介质相比,采用考虑饱和多孔介质的特性分析地基土较为合理。
[1]郑永来,刘曙光,杨林德,等.软土中地铁区间隧道抗震设计研究[J].地下空间,2003,23(2):111-118.ZHENG Yong-lai,LIU Shu-guang,YANG Lin-de,et al.A study on seismic design of subway tunnel in soft clay[J].Underground Space,2003,23(2):111-118.
[2]庄海洋,陈国兴.软弱地基浅埋地铁区间隧洞的地震反应分析[J].岩石力学与工程学报,2005,24(14):2506-2512.ZHUANG Hai-yang,CHEN Guo-xing.Earthquake response of shallow subway tunnels in soft foundation[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(14):2506-2512.
[3]刘晶波,李彬,谷音.地铁盾构隧道地震反应分析[J].清华大学学报(自然科学版),2005,45(6):757-760.LIU Jing-bo,LI Bin,GU Yin.Seismic response analysis of shielded subway tunnels[J].Journal of Tsinghua University(SCi&Tech),2005,45(6):757-760.
[4]蒋英礼,刘洋.软土地铁车站接头结构在强地震作用下的响应研究[J].铁道建筑,2010,(8):84-87.JIANG Ying-li,LIU Yang.Study on response of the joint of the soft soil-subway station under strong motion[J].Railway Engineering,2010(8):84-87.
[5]姜忻良,徐余,郑刚.地下隧道-土体系地震反应分析的有限元与无限元耦合法[J].地震工程与工程振动,1999,19(3):22-26.JIANG Xin-liang,XU Yu,ZHENG Gang.Finite element and infinite element coupling method for seismic analysis of soil-underground tunnel system[J].Earthquake Engineering and Engineering Vibration,1999,19(3):22-26.
[6]MAZZONI S,MCKENNA F,SCOTT M H,et al.OpenSees command language manual[M].[S.l.]:Pacific Earthquake Engineering Research(PEER)Center,2006.
[7]曾晨,孙宏磊,蔡袁强,等.简谐荷载作用下饱和土体中圆形衬砌隧道三维动力响应分析[J].岩土力学,2014,35(4):1147-1156.ZENG Chen,SUN Hong-lei,CAI Yuan-qiang,et al.Analysis of three-dimensional dynamic response of a circular lining tunnel in saturated soil to harmonic loading[J].Rock and Soil Mechanics,2014,35(4):1147-1156.
[8]YIAGOS A N,PREVOST J H.Two-phase elasto-plastic seismic response of earth dams:Applications[J].Soil Dynamics and Earthquake Engineering,1991,10(7):371-381.
[9]李伟华,赵成刚,杜楠馨.软弱饱和土夹层对地铁车站地震相应的影响分析[J].岩土力学,2010,31(12):3958-3970.LI Wei-hua,ZHAO Cheng-gang,DU Nan-xin.Analysis of effects of saturated soft interlayer on seismic responses of metro station[J].Rock and Soil Mechanics,2010,31(12):3958-3970.
[10]李亮,杜修力,赵成刚,等.流体饱和两相多孔介质动力反应计算分析[J].岩土力学,2008,29(1):113-118.LI Liang,DU Xiu-li,ZHAO Cheng-gang,et al.Calculation and analysis of dynamic response of fluid-saturated porous media[J].Rock and Soil Mechanics,2008,29(1):113-118.
[11]杜修力,赵密,王进廷.近场波动模拟的一种应力人工边界[J].力学学报,2006,38(1):49-56.DU Xiu-li,ZHAO Mi,WANG Jin-ting.A stress artificial boundary in fea for near-field wave problem[J].Chinese Journal of Theoretical and Applied Mechanics,2006,38(1):49-56.
[12]赵江倩,刘优平,余巍伟,等.地震加速度作用下饱和土中深埋隧道的动力响应[J].岩土工程学报,2013,35(增刊1):418-424.ZHAO Jiang-qian,LIU You-ping,YU Wei-wei,et al.Dynamic response of deep buried tunnels in saturated soil to effect of seismic acceleration[J].Chinese Journal of Geotechnical Engineering,2013,35(Supp.1):418-424.
[13]张鸿,高谦,徐斌,等.地震P 波作用下饱和土中考虑剪切与转动变形的衬砌结构动力响应分析[J].中南大学学报,2014,45(6):1943-1951.ZHANG Hong,GAO Qian,XU Bin,et al.Dynamic response of tunnel lining considering both rotary and shear deformation embedded in saturated soil with seismic P wave[J].Journal of Central South University(Science and Technology),2014,45(6):1943-1951.
[14]刘光磊,宋二祥.饱和无限地基数值模拟的黏弹性传输边界[J].岩土工程学报,2007,28(12):2128-2133.LIU Guang-lei,SONG Er-xiang.Visco-elastic transmitting boundary for numerical analysis of infinite saturated soil foundation[J].Chinese Journal of Geotechnical Engineering,2007,28(12):2128-2133.
[15]王子辉,赵成刚,董亮.流体饱和多孔介质黏弹性动力人工边界[J].力学学报,2006,38(5):605-610.WANG Zi-hui,ZHAO Cheng-gang,DONG Liang.A viscous-spring dynamical artificial boundary for saturated porous media[J].Chinese Journal of Theoretical and Applied Mechanics,2006,38(5):605-610.
[16]刘晶波,谷音,杜义欣.一致黏弹性人工边界及黏弹性边界单元[J].岩土工程学报,2006,28(9):1070-1075.LIU Jing-bo,GU Yin,DU Yi-xin.Consistent viscous-spring artificial boundaries and viscous-spring boundary elements[J].Chinese Journal of Geotechnical Engineering,2006,28(9):1070-1075.
[17]SILVIA M,FRANK M,MICHAEL H S.OpenSees users manual[R].Berkeley:PEER,University of California,2004.
[18]SCOTT B D,PARK R,PRIESTLEY M J N.Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J].ACI Journal,1982,79(2):13-27.
[19]KENT D C,PARK R.Flexural members with confined concrete[J].Journal of the Structural Division,ASCE,1971,97(7):1969-1990.
[20]MENEGOTTO M,PINTO P E.Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[C]// IABSE Symposium on Resistance and Ultimate Deformability of Structures.Lisbon:[s.n.],1973.
[21]刘如山.强地震动作用下地铁结构与土脱开滑移的研究[J].地震工程与工程振动,2004,24(6):136-141.LIU Ru-shan.The analysis of slippage and coming away between the subway structure and the soil subjected to strong ground motions[J].Earthquake Engineering and Engineering Vibration,2004,24(6):136-141.
[22]蔡隆文,谷音,卓卫东,等.基于有限元分析的振动台试验土箱边界效应研究[C]//第23 届全国结构工程学术会议论文集(第Ⅱ册).广州:[s.n.]:2014,10.CAI Long-wen,GU Yin,ZHUO Wei-dong,et al.Study on the boundary effect of the soil-box on shaking table based on finite element analysis[C]//Proceedings of 23rd Conference on Structure Engineering(Book II).Guangzhou:[s.n.]:2014,10.
[23]谌凯.基于振动台试验的地铁车站结构的地震反应分析[D].福州:福州大学,2014.CHEN Kai.Analysis of seismic responses of subway station based on shaking table tests[D].Fuzhou:FuzhouUniversity,2014.
