酒鬼酒股票收益率序列的多重分形特征

蒙 迅，黄 毅，吴生虎，谢志辉，史 凯

(1.吉首大学生物资源与环境科学学院，湖南 吉首 416000；2.吉首大学数学与统计学院，湖南 吉首 416000)



酒鬼酒股票收益率序列的多重分形特征

蒙 迅1，黄 毅2，吴生虎1，谢志辉1，史 凯1

(1.吉首大学生物资源与环境科学学院，湖南 吉首 416000；2.吉首大学数学与统计学院，湖南 吉首 416000)

运用多重分形消除趋势波动分析法，研究湘西酒鬼酒上市公司股票收益率的多重分形特征可知，股票收益率序列在不同尺度上均具有多重分形特征，验证了分形市场的假说.进一步运用相位随机替代法与随机重构法，对不同时间尺度上多重分形特征的动力原因进行分析可知，在小时间尺度上长期持续性占主导作用，而大时间尺度上尖峰胖尾与长期持续性共同作用导致多重分形特征的产生.

股票；收益率序列；多重分形特征；时间尺度

金融市场是一个非线性动力系统，通常表现出复杂的行为和不规则的现象.如何较全面地分析金融时间序列，进而了解其运行规律和波动特征，一直是人们关注的焦点问题.“有效市场假说”(EMH)是现代金融经济学的理论基石，该理论认为金融资产价格的变化相互独立，遵循随机游走模型.金融资产的价格波动不具有长期持续性，从而价格波动不具有可预测性.

然而，近几十年来，随着非线性随机动力系统与非线性随机微分方程的深入研究，诸多学者发现金融资产的价格波动在一定时间尺度内具有记忆性，即价格波动存在违背EMH的长期持续性特征[1].目前，经济物理学的研究普遍证实，在面对复杂的金融系统时，理想化、线性化的EMH无法正确且合理地解释许多经济现象.分形理论由Mandelbrot所创立，近年来发展迅速，被作为有效工具广泛应用于各种复杂系统的研究.在金融系统方面，分形解释了传统的EMH所不能解释的现象，说明金融市场具有分形特征，为此产生了分形市场假说(FMH)，该假法更符合实际.FMH认为金融资产的价格是以分数布朗运动的方式进行变动，具有尖峰胖尾和长期记忆性[2-6].Edgar E Peters[7]运用重标极差R/S分析方法发现一些金融市场具有长程相关性的依据.Cajueiro D O等[8]运用R/S分析方法研究了新兴市场的长程自相关性，发现随时间推移，市场变得越来越有效.Alvarez-Ramirez J等[9]通过单一分形来刻画金融市场的复杂性，运用消除趋势波动分析法(DFA)对美国股市不同时间段的Hurst指数进行分析，发现Hurst指数具有逐渐降低的发展趋势.但是，不同波动的概率不同，如果仅仅用单一分形来刻画金融市场的波动特性，就会忽略掉市场波动的许多重要信息.2002年，在DFA[10]的基础上，Kantelhardt Jan W等[11]提出多重分形消除趋势波动分析法(MFDFA).由于该方法不仅能够发现非平稳序列中的较长时间尺度上的相关性，而且能够将市场的波动划分为不同特征的点集，更加细致地刻画股市波动的动力特征，因此广泛应用于金融序列的研究[12-17].

酒鬼酒作为湖南省湘西自治州企业的代表，对整个湘西的经济社会发展有重要的影响.作为上市公司，其股票可以反映公司的运营情况.笔者以酒鬼酒股票的收盘价格为研究对象，运用MFDFA对其收益率序列进行分析，证明其股票价格收益序列具有多重分形特征，验证了FMH的存在，并分析了不同尺度下多重分形的来源.

1 多重分形消除趋势波动分析法

2002年，Kantelhardt Jan W等对DFA方法进行改进，得到多重分形消除趋势波动分析(MF-DFA)方法.该方法不仅能够避免对相关性的误判，而且能发现非平稳时间序列中的长程相关性，是检验非平稳时间序列是否具有多重分形特征的有效方法.

假设时间序列为p(i)(i=1，2，3，…，N)，N表示时间序列的长度，MF-DFA计算方法如下：

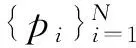
(5)确定波动函数的标度指数，对每一个确定的q值，存在幂律关系Fq(s)∝sh(q).

对每一个s，都可求出对应的Fq(s)，作出ln Fq(s)与ln s 的函数关系图，其斜率即为q阶Hurst指数h(q).当h(q)随着q的变化始终为常数时，即时间序列每一段消除趋势后的q阶波动相同，序列是单一分形；当h(q)为q的函数时，说明时间序列的局部结构并非一直均匀，序列为多重分形.当h(q)>0.5时，时间序列小的波动与大的波动表现出长期持续性，后一段时间序列的增加(减小)很大程度上依赖于前一段时间序列的增加(减小)，前后时段的涨落具有同向性；当h(q)<0.5时，时间序列小的波动与大的波动表现出反持续性，后一段时间序列的增加(减小)很大程度上依赖于前一段时间序列的减小(增加)，前后时段涨落具有反向性；当h(q)=0.5时，时间序列的波动属于随机游走，没有规律.其中q<0，h(q)描述的是时间序列小的波动情况，q>0，h(q)描述的是时间序列大的波动情况.h(2)是Hurst指数，所以h(q)也叫广义的Hurst指数.多重分形强度能有效地衡量时间序列的复杂程度，显而易见，较强的多重分形特征意味着h(q)的变化范围较大，因此多重分形强度可以通过Δh来衡量，Δh=q(min)-q(max).

2 酒鬼酒股票价格的统计分析

为了研究2008年金融危机后酒鬼酒股票价格的波动规律，选取2010年1月4日至2013年12月30日的日收盘价格(数据长度952个)作为研究数据，数据源于国泰安数据库(http:∥www.gtarsc.com/).

用p(t)表示第t天的收盘价，每天的对数收益率为r(t)=lnpt+1-lnpt，收益率序列数据个数为951个.图1，2给出了酒鬼酒股票的日收盘价格与日对数收益率，表1给出了日对数收益率的基本统计量.从表1可看出，酒鬼酒股票日对数收益率序列的偏度小于0，呈左偏状态，即收益率处于负值的概率比处于正值的概率大.股票日对数收益率序列的峰度4.56，比正态分布的峰度3大，而标准差远远小于正态分布的标准差1，说明日收益序列是非正态分布，具有尖峰胖尾特征.在95%的置信区间内，JB统计量为96.20，大于临界值10.15，酒鬼酒日对数收益率序列偏离正态分布.

图1 酒鬼酒股票日收盘价格

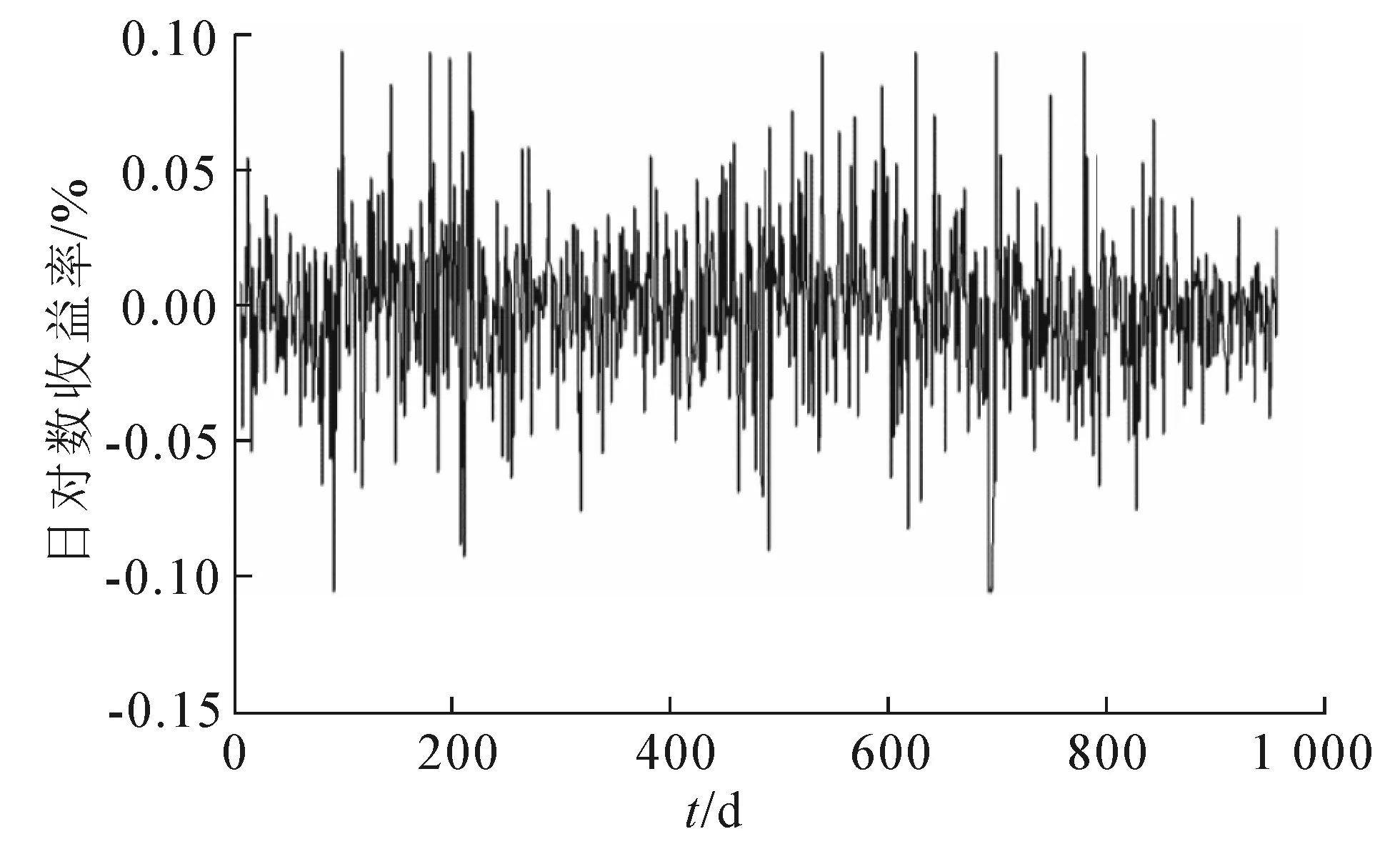
图2 酒鬼酒股票日对数收益率

样本数均值最大值最小值标准差偏度峰度JB统计量JB临界值951-1.57´10-40.096-0.140.03-0.054.5696.2010.15

3 多重分形的结果与讨论

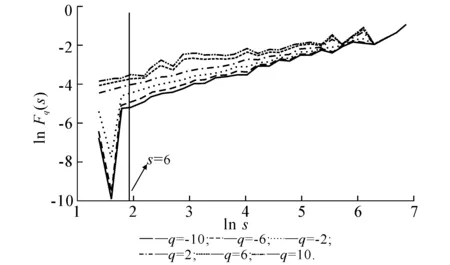
图3 酒鬼酒股票收益率ln Fq(s)～ln s的关系

运用MFDFA分析法对酒鬼酒股票的日对数收益率序列进行实证分析.在不同的分割长度s下，对每个固定的q值，用最小二乘法拟合，得到双对数ln Fq(s)～ln s的关系图.图3给出了q=-10，-6，-2，2，6，10共5条拟合线.由图3可知，从整体上来看，它们均呈现线性趋势；同时发现在ln s≈1.79(s=6)处存在突变点，即大约在1周的尺度上出现状态跃迁的临界点.

表2给出了不同时间尺度下(小时间尺度s<6，大时间尺度s>6)的标度指数.从表2可知，酒鬼酒股票日对数收益率序列，无论是在小时间尺度上还是大时间尺度上，其广义Hurst指数h(q)随q的变化而变化，表明酒鬼酒日对数收益率序列均具有多重分形特征，验证了FMH的存在.当s<6时，h(2)=0.74；当s>6时，h(2)=0.54.h(2)均大于0.5，表现出长期持续性特征，但在大时间尺度上其长期持续性要弱于小时间尺度.同时也发现，在小时间尺度上(s<6)，所有的广义Hurst指数均大于0.这表明日对数收益率序列无论是大的波动还是小的波动，在1周以内

表2 酒鬼酒股票收益率序列的广义Hurst指数

的时间尺度上，均表现出长期的持续性，即下一阶段股票的涨落很大程度上依赖于前一段时间的涨落.而在大时间尺度上(s>6)，当q≥4时，h(q)<0.5，具有反持续性.这表明在大于1周的时间尺度上，前一时段价格大幅上涨(下跌)，很可能在一定程度上决定了下一刻价格也许大幅下跌(上涨).长期持续性的动力特征是典型的正反馈机制的系统，它本质上是不稳定的；而反的持续性动力机制，意味着稳定的或者是负反馈机制[18]：因此，各种波动在小时间尺度上均是不稳定的.而在大时间尺度上，对于酒鬼酒股票市场，大的波动相对于与小的波动而言更为稳定.

表2给出了不同时间尺度下酒鬼酒股票日对数收益率的广义Hurst指数，而时间序列的多重分形强度依赖于Hurst指数的变化范围，即Δh的大小，Δh越大，多重分形强度越大，反之则越小[19].从表2可知，小时间尺度上(s<6)的Δh=3.9，远超过大时间尺度上(s>6)的Δh=0.34.这表明在不同的时间尺度上，酒鬼酒股票的多重分形强度不同，小时间尺度的多重分形强度要强.换而言之，在现实股票交易中，对于短期(1周以内)的交易者，他所面对的交易环境更为复杂，股票价格波动的影响因素更多，不仅依赖于国家政策、公司的经营情况以及市场的供应需求等因素，还受瞬息变化的市场影响，股票波动也更为剧烈.而对

于长期(1周以上)的交易者，他所面对的交易环境要简单一些，股票价格波动更多的是依赖于国家政策、公司的经营情况以及市场的供应需求，股票价格波动相对较小.

时间序列中的多重分形行为存在2种原因：一是时间序列的小幅波动及大幅波动在不同的时间尺度中的持续影响，即长期持续性；二是时间序列极端值的尖峰胖尾概率分布特性.可以根据以下2种方法分别鉴定这2种动力机制的来源：(1)通过相位随机替换方法构造替换序列，由于该序列完全消除了原始序列中的非线性特征，仅保留原始序列中的线性成分，因此替换序列能有效检验极值尖峰胖尾分布对多重分形的贡献大小，即如果替换序列的多重分形强度相比原始序列降低了，就说明尖峰胖尾分布对多重分形有影响，是产生多重分形的原因之一，否则尖峰胖尾对多重分形没有影响.(2)通过随机重构方法构造随机序列，由于该序列去除了原始序列内在的时间相关性，仅保留原始序列的非线性成分，因此随机序列能有效检验长期持续性对多重分形特征的作用大小，即如果随机序列的多重分形强度相比原始序列降低了，就说明长期持续性对多重分形有影响，是产生多重分形的原因之一，否则长期持续性对多重分形没有影响.

表2同样给出了不同时间尺度下替换序列和随机序列的h(q)值.图4给出了3组序列的q～h(q)关系.Δh反应了多重分形特征的强度.在小时间尺度上(s<6)，替换序列的Δh与原始序列的相近，而随机序列却相差很大，这说明在较小的时间尺度上，多重分形特征主要源自长期持续性作用，而尖峰胖尾分布作用很小；在大时间尺度上(s>6)，替换序列与随机序列的Δh均小于原始序列的，这说明在大时间尺度上，长期持续性与尖峰胖尾对日对数收益率序列的多重分形特征均有影响.

图4 q～h(q)

4 结语

首先通过对收益率序列基本统计量的分析，发现它是偏离正态分布的尖峰胖尾分布.随后运用MFDFA分析方法，研究日对数收益率序列的多重分形性，验证了分形市场的存在性.研究双对数坐标下波动函数发现，日对数收益率序列存在突变点(s=6).进而分析在不同时间尺度下日对数收益率的多重分形特征，发现广义Hurst指数h(q)依赖于q的变化，这意味着酒鬼酒日对数收益率序列存在多重分形特征.在较小的时间尺度上，大的波动与小的波动均表现出长期持续性；而在较长的时间尺度上，小的波动表现长期持续性，大的波动却表现出反持续性.比较不同时间尺度上多重分形的来源可知，小时间尺度上长期持续性是多重分形特征的主要来源，随时间尺度的增加，收益率序列的多重分形特征受长期持续性与尖峰胖尾共同作用.

[1] GIOVANNI BONANNO，FABRIZIO LILLO，ROSARIO N MANTEGNA.Levels of Complexity in Financial Markets[J].Physica A，2001，299:16-27.

[2] BENOIT B MANDELBROT，JOHN W VAN NESS.Fractional Brownian Motions，Fractional Noises and Applications[J].SIAM Review，1968，10(4):422-437.

[3] BENOIT B MANDELBROT.The Fractal Geometry of Nature[M].New York:W. H. Freeman Company，1982.

[4] ROSARIO N MANTEGNA，HARRY EUGENE STANLEY.An Introduction to Econophysics:Correlations and Complexity in Finance[M].Cambridge:Cambridge University Press，1999.

[5] 魏 宇，黄登仕.经济物理学研究评述[J].经济学动态，2002(7):74-78.

[6] 苑 莹，庄新田.我国沪铜期货价格的分形统计[J].东北大学学报:自然科学版，2008，29(1):137-140.

[7] EDGAR E PETERS.Chaos and Order in the Capital Markets[M].New York:John Wiley & Sons，1991.

[8] CAJUEIRO D O，TABAK B M.Long-Range Dependence and Multifractality in the Term Structure of LIBOR Interest Rates[J].Physica A，2007，373:603-614.

[9] ALVAREZ-RAMIREZ J，ALVAREZ J，RODRIGUEZ E，et al.Time-Varying Hurst Exponent for US Stock Markets[J].Physica A，2008，387(24):6 159-6 169.

[10] PENG C-K，BULDYREV S V，HAVLIN S，et al.Mosaic Organization of DNA Nucleotides[J].Physical Review E，1994，49(2):1 685-1 689.

[11] KANTELHARDT JAN W，STEPHAN A ZSCHIEGNER，EVA KOSCIELNY-BUNDE，et al.Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series[J].Physica A，2002，316:87-114.

[12] 苑 莹，庄新田，金 秀.基于MFDFA的中国股票市场多标度特性及成因分析[J].管理工程学报，2009，23(4):96-99.[13] WANG Yudong，WEI Yu，WU Chongfeng.Analysis of the Efficiency and Multifractality of Gold Markets Based on Multifractal Detrended Fluctuation Analysis[J].Physica A，2011，390(5):817-827.

[14] WANG Hui，XIANG Luojie，PANDEY R B.A Multifractal Detrended Fluctuation Analysis (MDFA) of the Chinese Growth Enterprise Market (GEM)[J].Physica A，2012，391(12):3 496-3 502.

[15] HU Shougeng，CHENG Qiuming，WANG Le，et al.Multifractal Characterization of Urban Residential Land Price in Space and Time[J].Applied Geography，2012，34:161-170.

[16] 张 林，刘春燕.日中两国不同经济时期股市的多重分形分析[J].系统工程理论与实践，2013，33(2):317-328.

[17] 孙艳红.允许卖空条件下证券投资组合的区间数线性规划问题[J].湖北民族学院学报：自然科学版，2014，32(3)：302-304.[18] TELESCA L，LOVALLO M，RAMIREZ-ROJAS A，et al.Scaling Instability in Self-Potential Earthquake-Related Signals[J].Physica A，2009，388:1 181-1 186.

[19] QIN Jing，LU Xinsheng，ZHOU Ying，et al.The Effectiveness of China’s RMB Exchange Rate Reforms:An Insight from Multifractal Detrended Fluctuation Analysis[J].Physica A，2015，421:443-454.

(责任编辑 向阳洁)

Multifractal Analysis of Stock Return Series of Jiugui Liquor Co. Ltd

MENG Xun1，HUANG Yi2，WU Shenghu1，XIE Zhihui1，SHI Kai1

(1.College of Biology and Environmental Science，Jishou University，Jishou 416000，Hunan China;2.College of Mathematics and Statistics，Jishou University，Jishou 416000，Hunan China)

Multifractal detrended fluctuation analysis has been used to research the multifractal characteristics of stock returns of Jiugui Liquor Co. Ltd in Xiangxi Autonomous Prefecture.The evidence shows that the return series are multifractal both for time scales smaller than a week and for time scales larger than a week，it also verifies the fractal market hypothesis about stock.Furthermore，the sources of multi-fractal characteristic are analyzed through shuffling procedure and phase randomization procedure at different scales.For time scales smaller than a week，the main contribution of multifractality is long-range correlations.For time scales larger than a month，both fat-tail distribution and long-range correlations play important roles in the contribution of multifractality.

stock;return series;multifractal characteristic;time scale

1007-2985(2015)04-0088-05

史 凯(1980—)，男，四川西昌人，吉首大学生物资源与环境科学学院副教授，博士，主要从事环境系统的非线性和复杂性研究.

F224；F830.91

A

10.3969/j.issn.1007-2985.2015.04.021