基于子空间追踪的稀疏信号重构算法

李 曙，毛承敏，杨 喜，尹 里，梁 俊

(吉首大学信息科学与工程学院，湖南 吉首 416000)



基于子空间追踪的稀疏信号重构算法

李 曙，毛承敏，杨 喜，尹 里，梁 俊

(吉首大学信息科学与工程学院，湖南 吉首 416000)

信号重构算法是压缩感知理论中的重要环节，其优劣影响压缩感知的重构效果.基于子空间追踪算法，对经稀疏表示和测量矩阵压缩后的信号进行重构验证，理论分析和实验结果表明，子空间追踪算法能使信号在较高压缩比下保持良好的重构效果.

子空间追踪；稀疏信号；信号重构；Nyquist采样

Nyquist采样定理指出，只有当信号采样频率高于或等于信号带宽的2倍时，采样得到的数字信号才能精确恢复原始信号.然而，随着现代通信和信号处理技术向更高频、更大数据量方向发展，如超宽带通信、太赫兹技术等，对信号的带宽要求越来越大，由此引发的采样频率、通信速率、存储空间的需求也越来越高.为了能以更低的成本和更高的效率满足这种需求，近年来人们致力于研究以远低于Nyquist采样频率对信号采样并恢复原始数据的技术.

1 压缩感知原理

图1 压缩感知示意

许多自然信号在时域上并不是稀疏信号，但在某个变换域上却是稀疏的.利用傅里叶变换、短时傅里叶变换、小波变换和Gabor变换等稀疏变换工具，将原始信号转换为变换域中的稀疏信号，这类信号称为可压缩信号[1].对于稀疏的或是可压缩的信号，可采用一种与Nyquist不同的采样理论,这就是Donoho D L等[2]于2006年提出的压缩感知理论.该理论证明了用远低于Nyquist采样频率对原始信号采样，得到的低维信号可以近乎完美地重构原始信号.信号压缩感知过程如图1所示.

图1中虚线所示部分为虚拟部分，在实际中不执行.令实际信号x∈Rn在某个变换域是稀疏的，变换矩阵为Ψ∈Rn×n，则x=Ψα.其中系数向量α∈Rn，是x的K稀疏表示.信号x经Ψ变换后变为稀疏信号，再经感知矩阵Φ∈Rm×n(m≪n)压缩便得到输出信号

y=ΦΨα.

(1)

由于压缩感知的输出信号y∈Rm(m≪n)，因此(1)式是一欠定的矩阵方程，无法得到该矩阵方程的解析解.当感知矩阵Φ满足约束等距条件

(2)

其中δK是一个与稀疏度K有关的常数，且0≤δK<1.

求解(1)式欠定矩阵方程的方法有多种，其基本思想是通过稀疏向量的支撑区的识别，将欠定的稀疏矩阵方程变换为超定的矩阵方程.常见算法包括基追踪(BP)[3]、正交匹配追踪(OMP)[4]、迭代硬阈值(IHT)[5]、子空间追踪(SP)[6]、梯度追踪[7]等.

2 子空间追踪算法

子空间追踪算法是稀疏信号重构算法的一种，与常规的匹配追踪类算法的原子选择机制类似.其不同之处在于子空间追踪算法引入了“回退机制”.对于K稀疏的信号，每次迭代过程中其标签集的候选列个数均为K，且其候选列在迭代过程中是动态更新的.正交匹配追踪算法在每次迭代过程中，其标签集中候选列的个数加1，且候选列一旦加入标签集将不会退出.因此，子空间追踪算法比匹配追踪类算法有更高的重建效率和更好的重建质量.其具体执行过程如下：

Input 稀疏度 K，感知矩阵,观测向量.

Initialize (1)Ω0={向量ΦTy中具有最大幅值的K个元素的标签集合}；

Iteration 对k=1,2,…,执行以下运算.

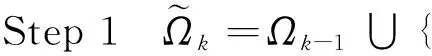
Step 3 Ωk={向量xp中具有最大幅值的K个标签集合}.

Step 5 若‖rk‖2>‖rk-1‖2,则令Ωk=Ωk-1，并退出迭代；否则令k=k-1,并返回Step 1,继续新一轮迭代.

3 稀疏信号重构实验

为验证信号重构的有效性，笔者利用子空间追踪(SP)算法分别对一维稀疏信号和二维图像信号进行重构实验.实验数据来源长度为256、稀疏度为30的高斯随机信号，测量矩阵为高斯随机矩阵.实验结果如图2所示.由图2可知，子空间追踪算法几乎完美地重构了原始信号，重构误差极小(在10-16数量级).

图2 一维稀疏信号重构实验结果

为更全面地衡量算法的有效性，将重构实验重复执行1 000次，在不同稀疏度下，运行时间及重构成功的概率如表1所示.随着稀疏度K的增大，重构耗时随之增大，重构成功率随之下降.稀疏度小于40时能准确重构，大于50时则重构成功率急剧下降.实验所用计算机配置为:intel至强双核CPU，主频3 GHz，内存为4 G，系统为Windows 8,实验软件为Matlab 2012b.

现以256×256的lena灰度图像作为二维图像信号实验对象，以随机高斯矩阵作为采样矩阵.先对原始图像进行小波变换，将其变换到小波域(二维图像信号在小波域中为稀疏信号).在采样长度M与图像长度N的比值α分别为0.3,0.4,0.5,0.6,0.7的情况下，利用子空间追踪方法重构的二维图像如图3所示.

表1 不同稀疏度下的重构耗时和成功率

图3 不同压缩比的二维图像信号重构结果比较

从图3的重构结果可知，在压缩比较小时，图像重构质量较差，随着压缩比增大，图像的重构效果越来越好.在压缩比α=0.5时已有较好的重构质量.同时，图像重构耗时也随压缩比的增加而增加.在不同压缩比的重构图像峰值信噪比(PSNR)及重构耗时如表2所示.

表2 不同压缩比的重构图像的PSNR值和耗时

4 结语

用子空间追踪算法对一维稀疏随机信号和二维图像信号进行重构验证，实验结果证明，当信号的稀疏度较小时，子空间追踪算法可以近乎完美地重构原始信号.算法的运算时间随着稀疏度的增大而增加，但重构效果随之变差.在实际应用中，某些场合的测量矩阵可能不满足约束等距性条件，其稀疏信号重构问题将是下一步的研究方向.

[1] 张贤达.矩阵分析与应用[M].第2版.北京：清华大学出版社，2013:82-84.

[2] DONOHO D L.Compressed Sensing[J].IEEE Transaction Information Theory,2006,52:1 289-1 306.

[3] CHEN S S,DONOHO D,SAUNDERS M.Atomic Decomposition by Basis Pursuit[J].SIAM Review，1998，43(1)：129-159.

[4] PATI Y C,REZAIIFAR R，KRISHNAPRASAD P S.Orthogonal Matching Pursuit:Recursive Function Approximation with Applications to Wavelet Decomposition[C]∥Proceeding 27th Asilomar Conference on Signals,Systems and Computers,1993：40-44.

[5] BLUMENSATH T,DAVIES M E.Iterative Thresholding for Sparse Approximations[J].The Journal of Fourier Analysis and Applications，2008，14：1-28.

[6] DAI W,MILENKOVIC O.Subspace Pursuit for Compressive Sensing Signal Reconstruction[J].IEEE Transaction on Information Theory，2009，55(5)：2 230-2 249.

[7] BLUMENSATH T,DAVIES M E.Gradient Pursuits[J].IEEE Transmation on Signal Processing,2008,56(6):2 370-2 382.

(责任编辑 陈炳权)

Sparse Signal Reconstruction Algorithm Based on Subspace Pursuit

LI Shu,MAO Chengmin,YANG Xi,YIN Li,LIANG Jun

(School of Information Science and Engineering,Jishou University,Jishou 416000,Hunan China)

Signal reconstruction algorithm plays an important part in the theory of compressive sensing and determines the reconstruction quality of compressive sensing.In this paper,based on the subspace pursuit(SP) algorithm,the signal is reconstructed after sparse representation and compression by the measurement matrix.Theoretical analysis and experimental results show that subspace pursuit algorithm can maintain good effect of signal reconstruction at higher compression ratio.

subspace pursuit;sparse signal;signal reconstruction;Nyquist sampling

1007-2985(2015)04-0023-03

李 曙(1985—)，湖南南县人，吉首大学信息科学与工程学院讲师，电子科技大学博士生，主要从事信号与信息处理研究.

TN911

A

10.3969/j.issn.1007-2985.2015.04.006