物流企业进入农村市场的冲突分析＊

雷 佳，李 晶

（西安工程大学 机电工程学院，西安710048）

目前我国城市物流市场日趋饱和，而农村市场的空白还有很多，特别是近年网购在农村的兴起，对农村物流的迫切程度又提升了一步，发展农村物流已经成为政府重点工作之一．面对城市物流的激烈竞争和农村市场的巨大潜力，诸多物流公司已然将扩展计划从城市移向了农村市场．

政府与物流企业分别需要做出怎样的行动，国内外已有不少学者提出自己的观点，文献［1-2］指出政府的政策导向与鼓励措施是物流企业开展环境管理实践的主要动机，但文中并未运用具体的数学模型验证观点．文献［3］讨论出农村物流发展的主导模式应主要以物流企业和商业企业联盟为主导模式，此中没有具体强调如何实施．文献［4］运用内容分析法验证了仅靠物流企业和相关市场主体的努力远远不够，还需要各级政府对物流进行引导与协调，文中所提的三个假设以经验数据验证，过于主观．文献［5］通过案例研究，仅得出政府的支持提高了物流企业的经济和环境绩效，没有得出共赢结局．文献［6-7］分别运用博弈分析得出结论，政府及物流企业为了获得长远的利益，政府制定奖惩制度，最后实现双方共赢．但是，在具体实施过程中，政府实施奖惩制度时要承担企业产出的不确定风险，同时还会涉及到企业与企业之间的合作与非合作关系的利益博弈关系等．

针对上述学者研究的不足，本文运用模糊综合评价法和冲突分析法相结合，在物流企业进入农村这一现实问题中，不仅对冲突事态进行结果预测和过程分析，提出解决问题的具体对策，同时，能够科学的确定局中人对自身目标折中的思维过程以及目标权重，最后得到合理稳定结局．

1 冲突分析基本理论及建模

冲突分析法是国外近年来在经典对策论和偏对策理论基础上发展起来的一种对冲突行为进行正规分析的决策分析方法［8］，它通过对许多难以定量描述的现实问题的逻辑思维分析，进行冲突事态结果预测和过程分析，帮助决策者科学周密的思考问题．但是，现有的冲突分析方法在应用时存在着一定的局限性：①局中人确定优先向量方面不能反映决策者对自身各目标折中的思维过程；②由于各类因素的特征不同，局中人确定不同因素影响程度的目标权重较为困难．本文将现有的冲突分析法做出改进，引入模糊综合评价法［9］．模糊综合评价法是利用模糊集理论进行评价的一种方法，它根据各类评价因素的特征，用精确的数字手段处理模糊的评价对象，确定评价值与评价因素之间的函数关系．引入模糊的思维方式，更接近东方人的思维习惯和描述方式，恰恰解决了定性评价转化为定量评价的难题，从而充分体现局中人对各自目标折中的过程．

1．1 改进后静态冲突分析法建模

冲突分析法包括五个要素：时间点、局中人、选择或行动、结局、优先序或优先向量，其中，改进后的优先序或优先向量运用模糊综合评价模型确定．

1）时间点指冲突开始发生时刻的标志，引入时间点的目的是为了对冲突问题的讨论明确化．

2）局中人指参与冲突的个人或集团．其必须由具有决策权的个人或集团构成，并且是较为明智的代表人物．

3）选择或行动是由于冲突在某一时刻的状态是各方决策者各自采取某些行为和动作构成的．这里，把这种经过提炼只能是采取与否的行为称为“行动”．每个决策者的一组行动的组合称为该决策者的一个策略．

4）结局即冲突的一种状态，当每个局中人选定一种方案后这些方案构成的结局集．需要注意的是，剔除从逻辑或偏好选择看来不可行的结局，得到可行结局集．

5）优先序或优先向量是局中人按照各自的目标要求及好恶标准，运用模糊综合评价对可行结局排出优劣次序，形成各自的优先序（向量）．

模糊综合评价法数学模型的建立步骤为

①建立评价因素集

选取若干个评价因素（资金、竞争力、企业形象、政策等）构成物流企业自身发展的模糊评价因素集U ＝ ｛u1，u2，u3，…，um｝．

② 建立评语（很希望、希望、一般、不希望等）集合（评价集）V ＝ ｛v1，v2，v3，…，vn｝．

评价集合的元素可以是非数量型的语言形式．

③ 建立权重集［10］．由于因素集中的各个因素对评价目标的影响程度各不同，为了反映各个因素的重要程度，这里对各个因素ui分别分配一个相应的权重zi并组成权重集Z．由于权重zi表示因素ui对“重要性”的隶属度，即

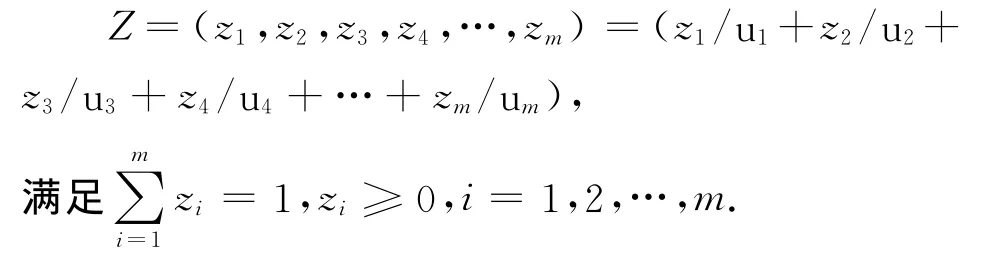
④ 建立单因素评价矩阵．从一个因素出发，对评判对象进行评判，可以得到单因素评判集Ri（i＝1，2，3，…，m），最后，可得到单因素的评判矩阵R ＝ ［R1，R2，R3，… Rn］T．

1．2 动态冲突分析建模

动态分析是在静态分析的基础上进行的．对动态冲突问题进行建模分析时，通常将冲突看成一个在各个时刻都存在可行结局的动态发展过程．冲突事件的局中人在各个时刻，都从自身利益出发，确认使自身更好的状态转移方式，并由此构成该局中人的个体状态转移矩阵．然后，求出冲突事件中所有局中人共同作用构成的整体状态转移矩阵，确定冲突事件的最终状态［11］，即冲突过程的结果．

根据静态分析的已知资料确定每一个局中人的个体转移矩阵，确定不可能转移到的状态，而后结合所有局中人的个体转移矩阵确定整体状态转移矩阵，最后通过对状态转移方程的运算，得到冲突问题的最终稳定解．

1）个体状态转移矩阵

进行状态转移分析时，先由各局中人根据自身的价值观和偏好将可行结局中的元素即状态，给出向其他状态及当前状态的转移概率，构成各局中人的个体状态转移矩阵．

2）整体状态转移矩阵

在个体状态转移矩阵的基础上，根据以下原则确定整体状态转移矩阵：

① 由个体状态转移矩阵计算全局状态转移矩阵中的一个结局，利用公式计算为

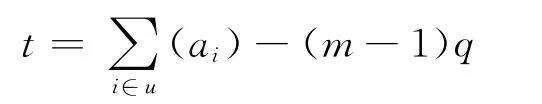
式中：t为所求可行结局所在的行位置；ai为局中人i由结局q转移后的结局；q为个体状态转移矩阵中该列对应的结局；u为所有个体状态转移矩阵发生单方面改进所组成的集合，m是u中元素的个数，即参加冲突的人数［12］．

②某个结局对所有的局中人都是吸收状态，则该结局的主元取1；某个结局对一个局中人有转移概率，对所有其他局中人都是吸收状态，则该结局向各结局的转移概率与该局中人的转移概率相同．若某个结局对几个或全部局中人有向各结局的转移概率，则用公式［12］计算为

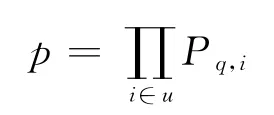
式中：p为所得结局对应的概率，即所有局中人共同作用产生的转移概率；Pq，i为局中人i由结局q转移得到新结局的概率．结合各局中人的个体状态转移矩阵，依据上述原则得到整体转移矩阵T．

2 模型求解

2．1 运用模糊综合评价法对优先向量排序

即将权重矩阵与单因素评价矩阵进行模糊合成运算，可得综合评价矩阵为

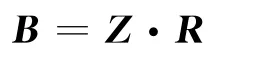
模糊合成算子常用矩阵乘积进行运算．

2．2 稳定性分析

稳定性分析解决从所有可行结局中求得平衡结局的问题．在这个过程中，有三个先决条件：①各局中人都会通过不断改变策略以追求自身利益的最大化；②局中人在做决策时都会考虑到其他局中人可能的反应行为，以及对自己的影响；③平衡结局必须是能被所有局中人共同接受的结局．

2．3 对状态转移模型求解

对于有n个可行结局的冲突问题，其状态转移方程Y＝TX．其中Y，X均为n×1维向量，T是n×n阶矩阵；Y，X，T的每一行都与某个特定的结局对应，T的各列与它们对应行同一结局相对应；X称为状态控制向量，每行的取值表示冲突在某一时刻的结局转成下一时刻的结局的概率，而且所有概率之和为1；矩阵T的每一列元素和也是1，且每个元素表示该列标志的结局转向本元素所在列对应行结局的概率；吸收状态是指列上只有对应本结局的行上为数字1的结局［12］．

3 算例分析

分别运用静态和动态分析的方法分析农村物流的现实问题．其中，静态分析过程中能够保存一定的现实信息，同时能快速找到最可能的平稳结局．而由于现实冲突问题的全过程及其内外部的环境因素不稳定，冲突分析技术必须能够追踪、处理和评估这种局势的动态变化，因此，动态分析过程与现实更接近，能够准确预测冲突事件发展的过程．

3．1 静态冲突分析建模与计算

冲突分析发生的时间点确定为2014年2月25日，利益参与者有物流企业、政府、农村居住人，其中农村居住人在此冲突事件中没有独立行动，所以局中人是物流企业和政府．物流企业有两种行动，①扩大市场，在农村布局网点；②将已有的城区市场加大投资力度．政府也有两个行动，即对企业的补贴和惩罚．总结局数22＋2＝16．剔除不可行结局后的结局见表1．

表1 可行结局表Tab．1 Feasible outcome

利用模糊综合评价法确定各局中人优先向量．

首先考虑用“资金”、“竞争力”、“企业形象”和“政策”四个指标来以物流的企业角度进行评价这一方案记为

在此基础上，进行单因素评价，利用专家打分法可得到对“资金”的模糊隶属度为

R1（资金）→ ｛0．5／很希望，0．3／希望，0．2／一般，0．0／不希望｝

同理得到其余三个指标的隶属度，略去评价语，得到单因素评价矩阵R，即模糊关系矩阵

结果表明物流企业在参与这一方案的态度中“很希望”的比例为32%，“希望”为30%，“一般”为24%，“不希望”为14%．同理可得到政府在这一方案中所持态度，稳定性分析见表2．

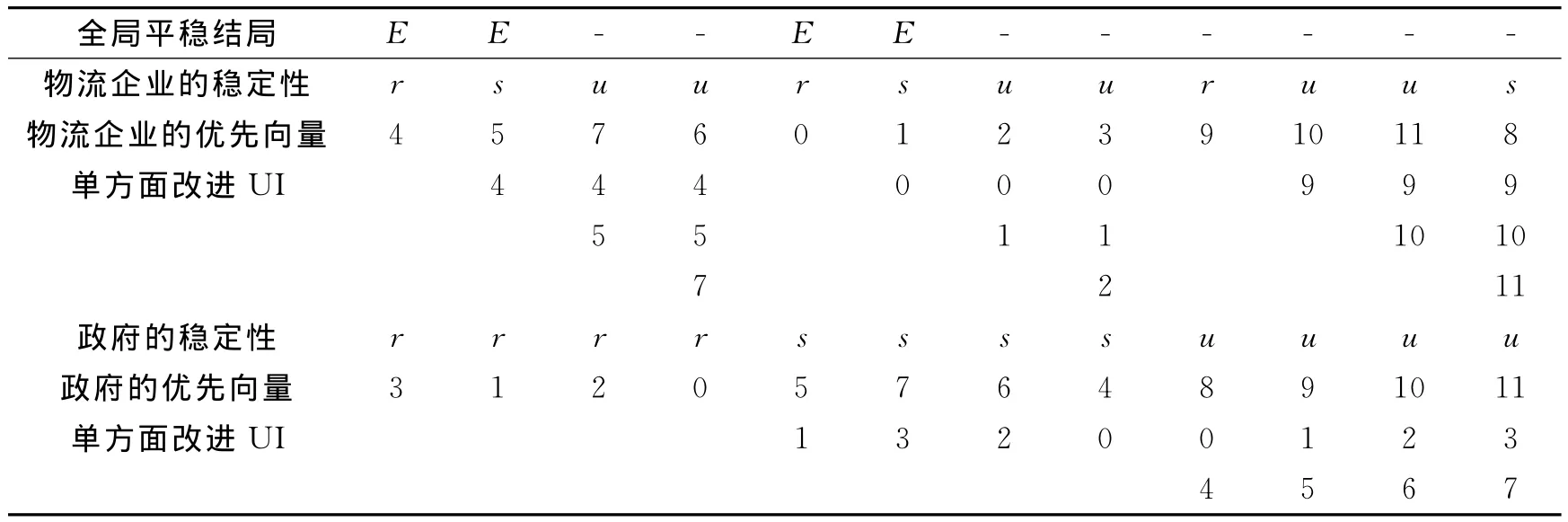
表2 稳定性分析表Tab．2 Stability analysis

由此可知，结局4，5，1，0是合理稳定性结局，为了比较其最优性，采用稳定度H［13］为

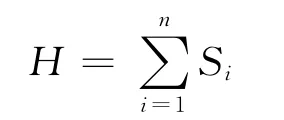
其中Si表示第i个局中人的稳定值，i＝1，2．稳定度越小越稳定，越可能成为最终结局，如结局4，处于物流企业优先向量的第1位，处于政府优先向量的第8位．于是，可以把结局4表示为4（1 r，8 r），类似的将结局5，1，0分别表示为5（2 r，5 r），1（6 r，2 r）和0（5 r，4 r），可得到：H4＝9，H5＝7，H1＝8，H0＝9，可知结局5稳定度最低，即物流企业应积极扩大自己的市场，同时政府给予相应的补贴是稳定性结局．

3．2 动态冲突分析建模与计算

由于各局中人在冲突事件的各个时刻都存在可行结局的动态发展过程，综合静态分析的12种可行性结局，根据物流企业和政府部门各自不断改变策略以达到对自身最有利的局面，同时考虑对方可能做出的反应，确定各局中人的个体状态转移矩阵，分别见表3～5．在个体状态转移矩阵的基础上，计算出整体转移矩阵T，分析动态结果．

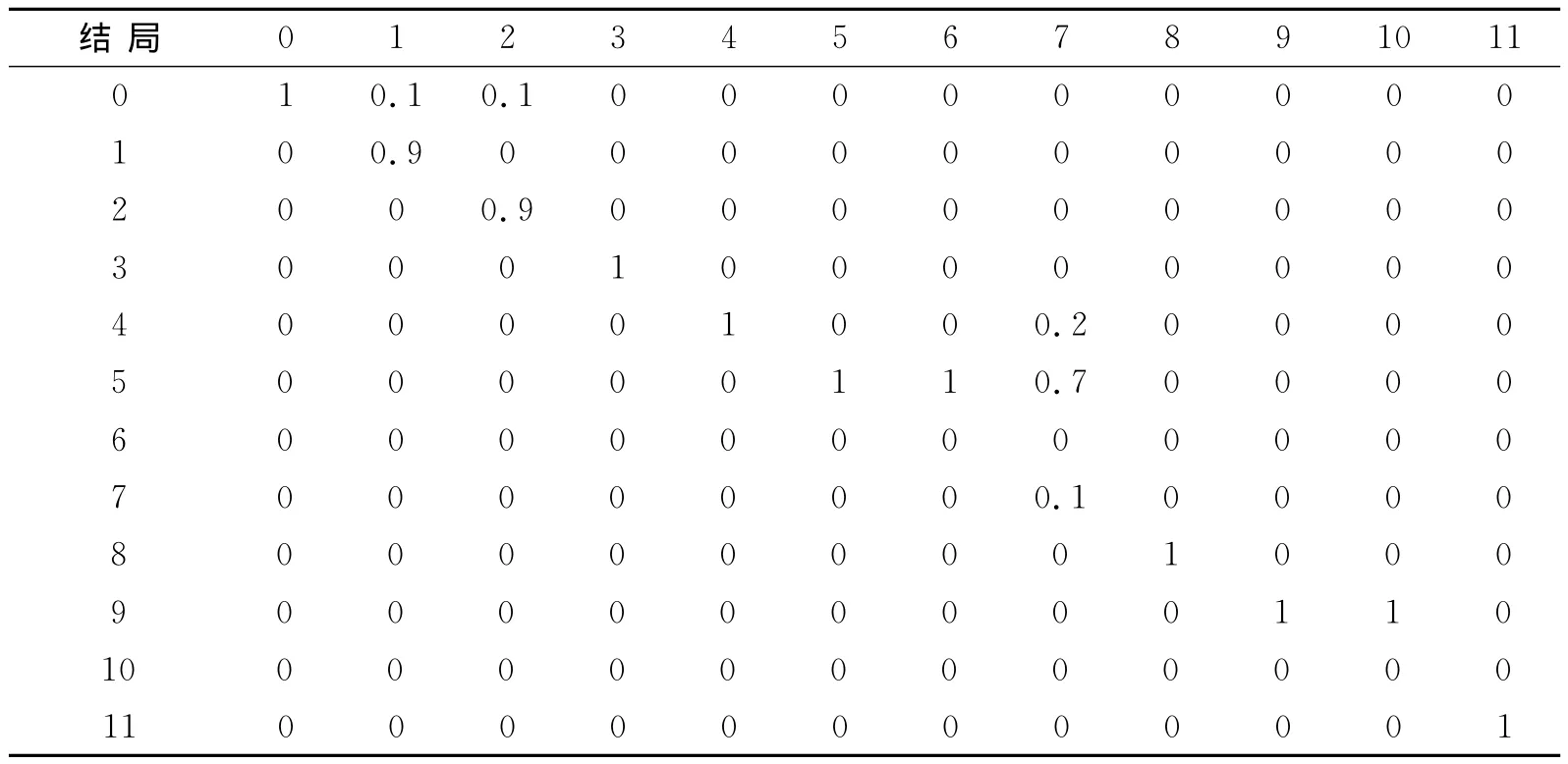
表3 物流企业的状态转移矩阵TwTab．3 State transition matrix Twof logistics enterprises

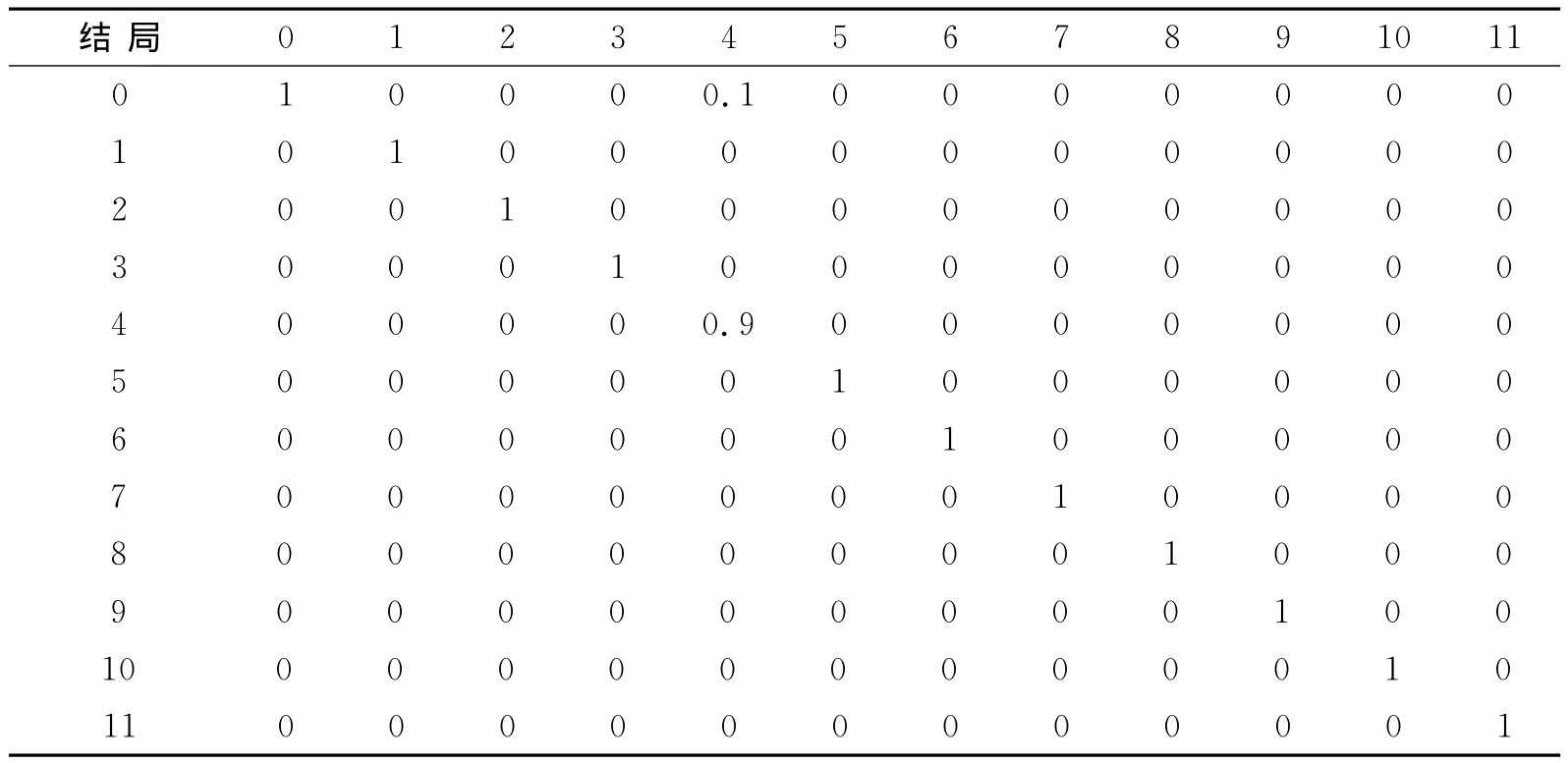
表4 政府的状态转移矩阵TzTab．4 The state transition matrix Tzof Government

用状态转移方程Y＝TX追踪冲突事件的发展过程，这里选择状态控制向量为X0＝（0，0，0，0，0．2，0．7，0，0．1，0，0，0，0）T结局0→0的概率为1）作为现状结局进行计算．根据状态矩阵转移方程：Y1＝TX0，Y2＝TY1，Y3＝TY2，Y4＝TY3，Y5＝TY4，…，Yn＝TYn-1（n，Yn＝X）［11］，计算得出结果见表6．

从均衡求解过程可以看出，动态分析结果是由结局7，即物流企业加大已有市场投资的同时扩大农村市场，政府给予相应的补贴，向结局4（物流企业既不扩大市场也不加大投资从而得到政府的补贴）、结局0（物流企业均不采取任何行动）稳定，最终稳定到结局5，即物流企业积极扩大农村市场，同时政府给予相应的补贴．稳定性最好的结局与静态分析结局一致，同为结局5：物流企业主动扩大农村市场，政府部门给予补贴的合作结局．

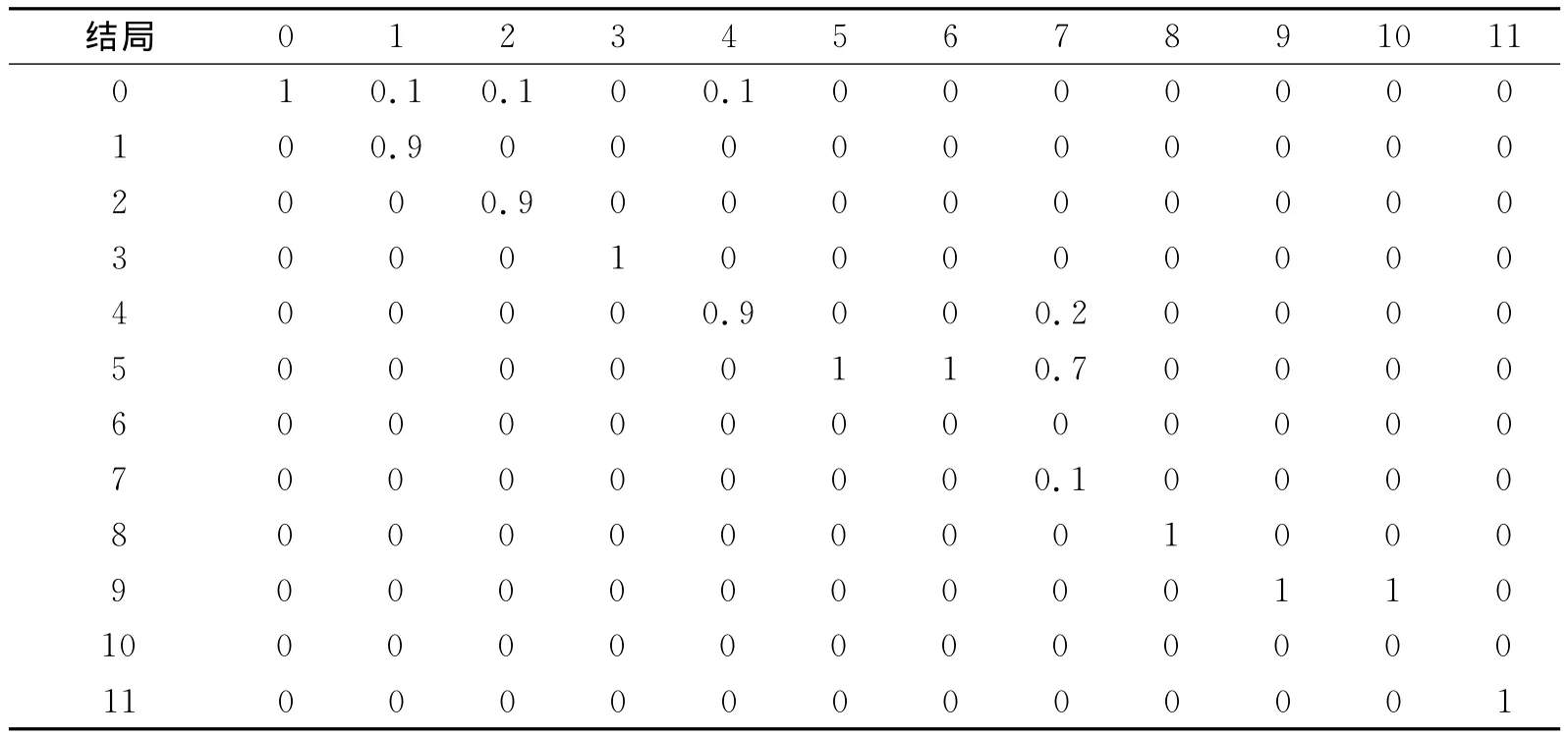
表5 整体状态转移矩阵TTab．5 Overall state transition matrix T

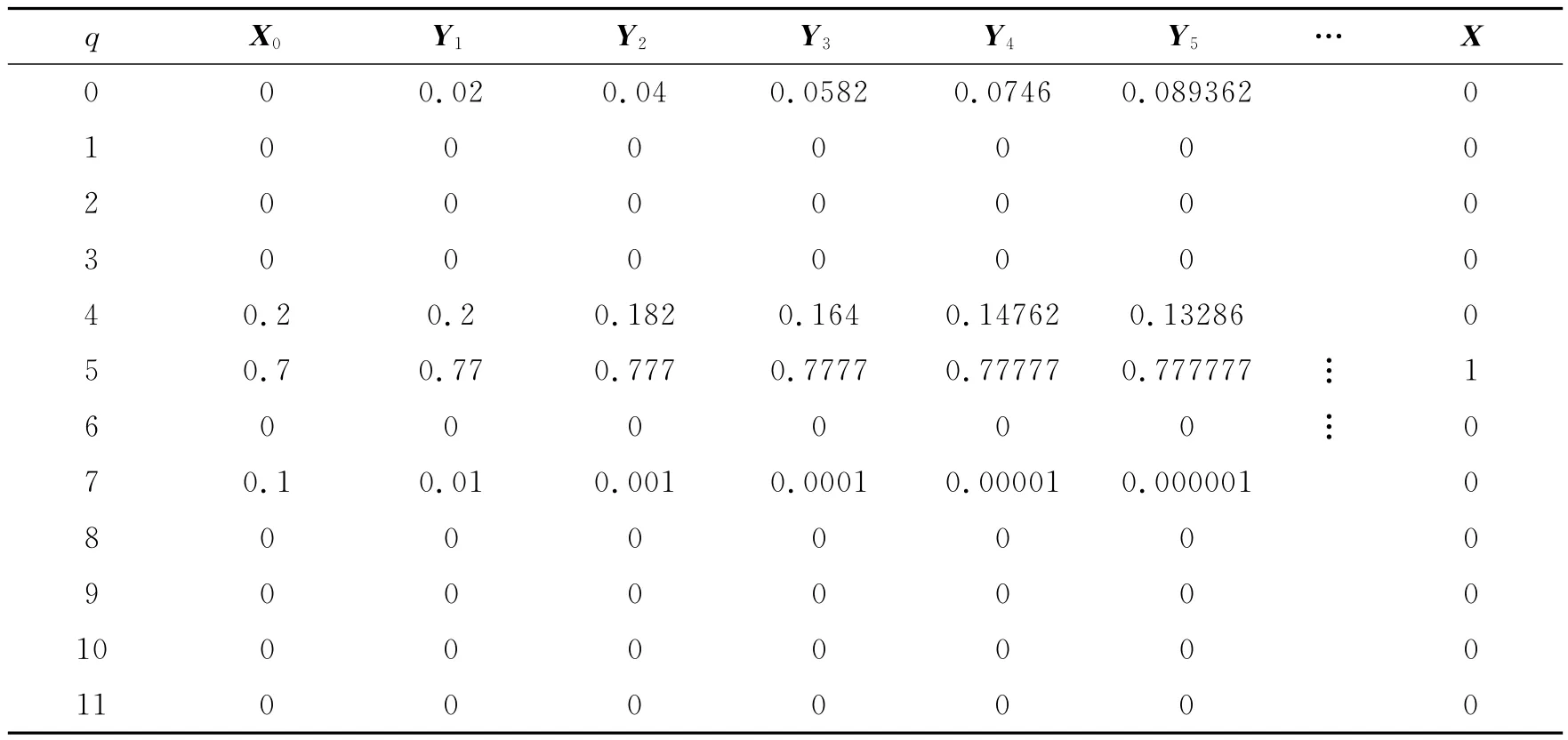
表6 求解过程Tab．6 Solving process

4 结 论

文中考虑了物流企业和政府部门的态度与利益，运用改进冲突分析法，研究了物流企业进入农村市场这一冲突问题．建立物流企业与政府部门的冲突模型，针对模型进行了理论分析，并通过计算详细分析，认为对于物流企业，需采纳政府部门提出的意见，扩大市场，不仅是对企业形象的提升，同时是对企业自身资本的增值和收益的最大化。对于政府相关部门，做到鼓励物流企业参与发展农村物流项目，提高市场在农村物流领域的资源优化配置作用．同时还要扶持一批农村物流龙头企业，使其发挥规模大、功能全、技术先进、现代化程度高的优势．文中对我国物流企业进入农村市场现状做了理论上分析研究，为政府和物流企业的权益达到共赢提供了借鉴和参考．

［1］ GREEN K，MCMEEKIN A，IRWIN A．Technological Trajectories and R＆D for Environmental Innovation in UK Firms［J］．Futures，1994，26（10）：1047．

［2］ FLORIDA R．Lean and Green：The Move to Environmentally Conscious Manufacturing［J］．California Management Review，1996，39（1）：80．

［3］ 白艳静．基于物流网络资源整合的我国农村物流发展模式研究［D］．北京：北京交通大学，2012．BAI Yan-jing．Study on Rural Logistics Development Mode Based on Logistics Network Resource Integration［D］．Beijing：Beijing Jiaotong University，2012．（in Chinese）

［4］ 陈青兰，赵梦楚．政府行为对物流企业战略影响的实证分析［J］．厦门理工学院学报，2012，20（1）：87．CHEN Qing-lan，ZHAO Meng-chu．A Game Analysis on Trade Conflicts Between Chinese Suppliers and Multinational Retailer［J］．Journal of Xiamen University of Technology，2012，20（1）：87．（in Chinese）

［5］ ZHU Q H，COTE R P．Integrating Green Supply Chain Management into an Embryonic Eco-Industrial Development：A Case Study of the Guitang Group［J］．Journal of Cleaner Production，2004，12（8）：1025．

［6］ 胡愈，许红莲．农村物流金融“地融仓”模式运行的博弈分析［J］．系统工程，2013，5（5）：47．HU Yu，XU Hong-lian．A Game Analysis of the Rural Logistics Finance “Land-Financing Warehouse”Mode Operation［J］．Systems Engineering，2013，5，（5）：47．（in Chinese）

［7］ 朱庆华，窦一杰．绿色供应链中政府与核心企业进化博弈 模 型 ［J］．系 统 工 程 理 论 与 实 践，2007，12（12）：85．ZHU Qing-hua，DOU Yi-jie．An Evolutionary Model Between Governments and Core-En-terprises in Green Supply Chains［J］．Systems Engineering：Theory ＆ Practice，2007，12（12）：85．（in Chinese）

［8］ 汪应洛．系统工程［M］．4版．北京：机械工业出版社，2003．WANG Ying-luo．Systems Engineering［M］．4th ed．Beijing：Mechanical Industry Press，2003．（in Chinese）

［9］ 王长琼．物流系统工程［M］．北京：高等教育出版社，2007．WANG Chang-qiong．Logistics System Engineering［M］．Beijing：Higher Education Press，2007．（in Chinese）

［10］ 祝建军，蒲云，胡敏杰．基于模糊综合评价的物流企业融资效率研究［J］．经济经纬，2006，5：135．ZHU Jian-jun，PU Yun，HU Min-jie．A Study of Logistics Enterprises Financing Efficiency Based on Synthetic Fuzzy Evaluation［J］．Economic Survey，2006，5：135．（in Chinese）

［11］ 王意冈，申金升．动态冲突分析及其在微观决策中的应用［J］．管理工程学报，1994，8（3）：58．WANG Yi-gang，SHEN Jin-sheng．Dynamic Conflict Analysis and Its Application in Microdecsion Making［J］．Journal of Industrial Engineering and Engineering Mansgement，1994，8（4）：58．（in Chinese）

［12］ 陈金亮，徐渝，苏兵．企业物流运营模式的选择分析［J］．运筹与管理，2004，10（5）：95．CHEN Jin-liang，XU Yu，SU Bing．Analysis of Enterprise Logistics Mode Decision［J］．Operations Research and Management Science，2004，10（5）：95．（in Chinese）

［13］ 薛顺利，柴国荣，宋悦林．多局中人冲突分析及其在经营城市中的应用［J］．西安工程大学学报，2005，6（2）：134．XUE Shun-li，CHAI Guo-rong，SONG Yue-lin．Multi-Player Conflict Analysis and Its Application in the Course of City Management［J］．Journal of Xi’an Polytechnic University，2005，6（2）：134．（in Chinese）