弹道修正弹的指数趋近律姿态控制＊

黎海青，栗金平，黄旭磊，杨 凯，王 冬

（中国兵器工业第203研究所，西安710065）

二维弹道修正弹是在普通炮弹的基础上，加装修正组件，使常规弹药获得精确打击能力，从而提高毁伤效率、减小附带毁伤并且极大降低作战成本［1］．弹道修正的主要原理是在飞行过程中测量弹丸位置、速度等信息，再利用执行机构改变弹丸弹道，提高命中精度．目前，基于固定翼的弹道修正技术成为研究热点．该方法结构简单，修正原理简明，并能够进行连续修正，其中滚转姿态控制是实现弹道修正的关键．关于修正组件滚转姿态控制的研究较少，文献［2-4］对固定翼二维修正弹进行了初步建模，并对飞行稳定性进行了仿真分析；文献［5］建立了二维修正引信滚转通道控制模型，并设计了双闭环控制算法；文献［6］设计了二维修正引信滚转自动驾驶仪，并通过仿真证明双旋修正引信滚转姿态可控．

文中针对弹道修正弹滚转姿态控制问题，研究了一种基于指数趋近律的变结构控制方法．基于固定翼／可动翼组合的双旋弹修正原理，通过受力分析建立其滚转通道状态空间模型，采用指数趋近律滑模理论设计滚转姿态控制律，通过数学仿真验证该控制律效果．

1 修正组件工作原理

文中以一类固定翼／可动翼组合修正弹为对象，进行滚转姿态控制方法研究．该修正弹由修正组件和弹体两部分组成，其中修正组件可以相对炮弹弹体自由滚转．修正组件表面安装两对翼，一对同向固定翼用于提供修正升力，一对可动翼用于控制组件滚转姿态．弹体相对惯性系高速旋转，保持弹体稳定，修正执行机构布局如图1所示．

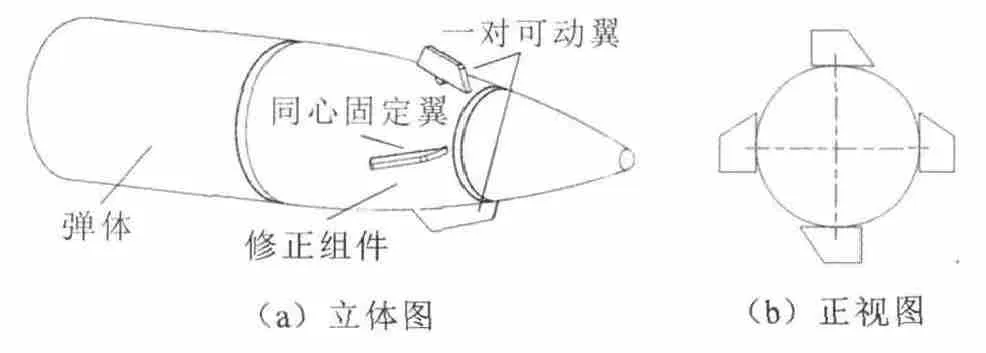
图1 修正执行机构布局Fig．1 Schematic diagram of layout of correction actuator

二维修正弹利用系统原有的飞行稳定性简化控制系统设计，采用“单通道控制、二维修正”的工作原理，即通过控制升力翼面的滚转姿态来提供特定方向的修正力，修正弹道轨迹，使弹丸飞向目标位置．建立修正组件坐标系Mxpypzp，坐标系原点为炮弹质心M，oyp与同向固定翼同轴，ozp与可动翼同轴，oyp与准弹体系y轴夹角为γ．根据修正需要，控制升力翼面滚转姿态角γ与期望滚转姿态一致，提供该方向修正力Fc，修正原理如图2所示．

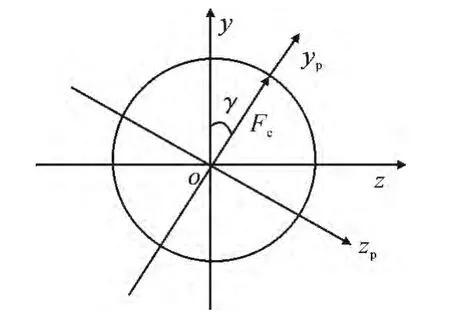
图2 修正原理示意图Fig．2 Schematic diagram of correction principle

2 修正组件控制模型

以带同向翼、差动翼的修正组件为研究对象，建立系统滚转通道控制模型．考虑修正组件滚转运动方程［7］表达式为

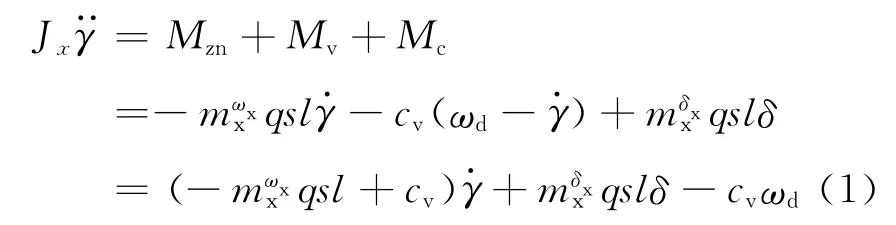
式中：Jx为组件转动惯量；Mzn为组件滚转阻尼力矩；Mv，Mc分别为摩擦力矩和控制力矩；mωxx为滚转阻尼力矩系数；cv为黏性阻尼系数；mδxx为差动翼效率；q为动压；s为差动翼投影面积；l为特征长度；δ为可动翼偏转角；ωd为弹体转速，可将cvωd项当作干扰项，具体参数计算见文献［7］．

在此，研究对象为二阶系统．由式（1）可得修正弹滚转通道的状态空间模型为

3 滑模变结构的姿态控制律设计

3．1 基于指数趋近律的变结构控制

变结构控制系统动态响应由两部分组成，对应两种性质的运动．第一阶段为切换面外运动，即趋近模态；第二阶段为切换面上的运动，即滑动模态［8］．合理设计两个阶段运动可以保证较好的控制品质．

系统状态方程为

式中：x为系统输入变量；A，B为状态方程系数矩阵；u为反馈量．

将变结构控制理论用于控制律设计，首先确定滑模面s来保证趋近运动有较好的动态特性，表达式为

其中C为状态方程系数矩阵．

构造指数趋近律表达式为

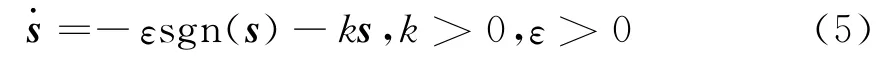
式中：-ks 为指数 趋 近 项，其值 为s（0）e-kt；-εsgn（s）为等速趋近项；k，ε为控制参数．指数趋近项反映运动点从远到近趋近滑模面的速度成相应指数规律．在趋近过程中，趋近速度从一较大值逐步减小到零，缩短了运动时间，使运动点到达切换面时速度很小．等速趋近项系数反映运动点趋近滑模面的恒定运动速度，到达切换面时增加等速趋近项，使趋近速度不为零［9］．在指数趋近律中，为保证快速趋近的同时削弱抖振，应增大k同时减小ε．

选取滑模面s＝Cx，选取指数趋近律构造s·＝-εsgn（s）-ks，必定有ss·＜0，由李亚普诺夫稳定性理论易知，系统必定向滑模面运动．

3．2 基于变结构控制的滚转姿态控制律设计

文中主要研究弹道修正过程中的修正组件滚转姿态控制问题，在此给出了基于趋近律的滑模控制律设计方法．考虑被控对象为

式中：γc为滚转姿态控制指令；c为系数；e为跟踪误差．

4 仿真及分析

文中弹道修正弹在飞行过程中有空间稳定和匀速转动两个状态．当需要进行弹道修正时，修正组件跟踪并稳定在期望的滚转姿态，可看成跟踪阶跃信号；当不需要进行弹道修正时，修正组件以定转速匀速转动，可看成跟踪斜坡信号．为验证控制律在不同状态下的控制效果，设计了两组滚转姿态指令．t为时间，t1、t2均为阶跃时刻．

1）阶跃信号

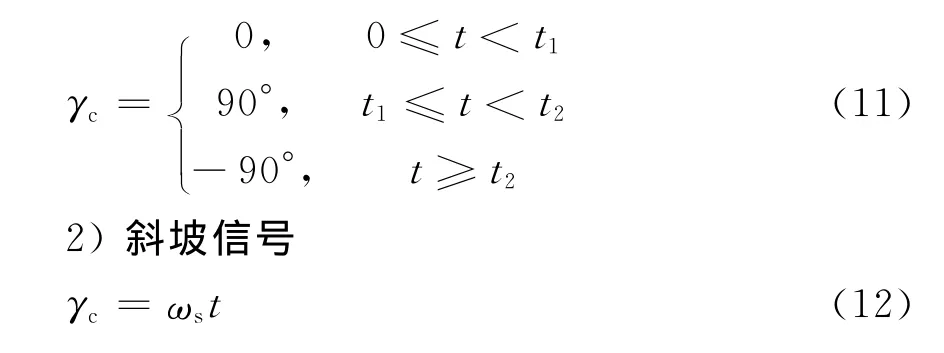
其中ωs为组件滚转角速度，设为720°·s-1．

等效动压可以反映整个飞行过程中高度、速度变化，故设计控制律时考虑最大动压和最小动压条件．经仿真计算可知在最大动压和最小动压处弹体滚转特性差别较大，见表1．在设计滚转姿态控制参数时，选取较大趋近参数和较小的等速趋近参数，以获得快速、精确的控制效果．选取控制参数c＝10，ε＝0．3，k＝8．

表1 修正组件弹体特性参数Tab．1 Projectile parameters of correction component

利用Simulink软件建立滚转通道仿真模型，取最大动压和最小动压两个条件分别进行仿真，仿真结果如图3～6所示．

图3 大动压条件下阶跃指令响应Fig．3 Step command response in large hydrodynamic condition

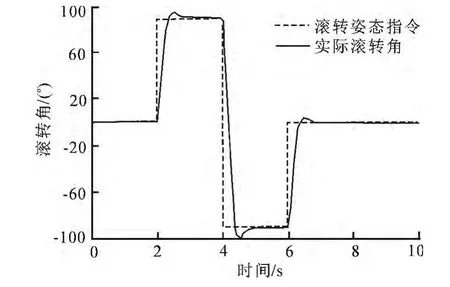
图4 小动压条件下阶跃指令响应Fig．4 Step command response in small hydrodynamic condition

由图3～4可知，大、小动压条件下跟踪±90°阶跃指令，系统调整时间均小于0．5s，表明修正组件滚转姿态能快速转动到期望的角度．由图5～6可知，大、小动压条件下修正组件能够稳定跟踪斜坡指令，即可实现修正组件匀速转动．由以上仿真结果可知，该滚转姿态控制律能适应动压较大范围变化，实现修正组件滚转姿态快速跟踪．

图5 大动压条件下斜坡指令响应Fig．5 Ramp command response in large hydrodynamic condition

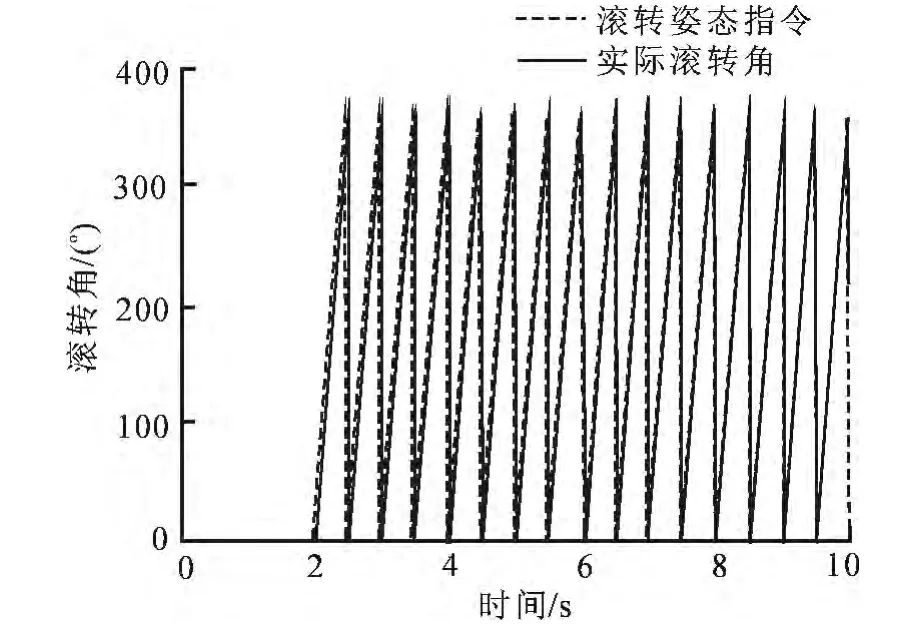
图6 小动压条件下斜坡指令响应Fig．6 Ramp command response in small hydrodynamic condition

5 结 论

1）为了实现固定翼／可动翼组合的弹道修正弹滚转姿态控制，建立了修正组件滚转通道控制模型，采用指数趋近律变结构控制理论，设计了滚转姿态控制器．

2）在大、小动压条件下，该控制器可实现修正组件滚转姿态快速跟踪，阶跃指令调整时间均小于0．5s，表明该控制器可适应动压大范围变化．

［1］ 孙新．弹道修正弹鸭舵修正方法研究［D］．南京：南京理工大学，2005．SUN Xin．Study on the Correction Method of the Trajectory Correction Projectile［D］．Nanjing：Nanjing University of Science ＆ Technology，2005．（in Chinese）

［2］ 揭涛，施坤林．旋转稳定弹弹道修正引信减旋装置研究［J］．探测与控制学报，2007，29（5）：9．JIE Tao，SHI Kun-lin．Study on Despining Device of Course Correction Fuze for Spin-Stabilized Projectile［J］．Journal of Detection ＆ Control，2007，29（5）：9．（in Chinese）

［3］ 常思江，王中原，刘铁铮．鸭式布局双旋弹飞行动力学建模与仿真［J］．弹道学报，2014，26（3）：1．CHANG Si-jiang，WANG Zhong-yuan，LIU Tie-zheng．Modeling and Simulation of Flight Dynamics for Dualspin Stabilized Projectile Equipped with Canards［J］．Journal of Ballistics，2014，26（3）：1．（in Chinese）

［4］ WERNERT P．Stability Analysis for Canard Guided Dualspin Stabilized Projectiles［C］／／AIAA Atmospheric Flight Mechanics Conference．Chicago：AIAA Atmospheric Flight Mechanics Conference，2009：10．

［5］ 高铭泽，施坤林，霍鹏飞，等．引信滚转角双闭环控制算法［J］．探测与控制学报，2013，35（3）：17．GAO Ming-ze，SHI Kun-lin，HUO Peng-fei，et al．Double Closed Loop Control Algorithm of Fuze Roll Angle［J］．Journal of Detection ＆ Control，2013，35（3）：17．（in Chinese）

［6］ VILJOEN G，PLESSIS R D．Desgin and Roll Attitude Control of a 2DGuided Fuze Kit［C］／／26th International Symposium on Ballistics．Miami：Journal of Applied Mechanics，2011：12．

［7］ 钱杏芳，林瑞雄，赵亚男．导弹飞行力学［M］．北京：北京理工大学出版社，2000．QIAN Xing-fang，LIN Rui-xiong，ZHAO Ya-nan．Missile Flight Aerodynamics［M］．Beijing：Beijing Institute of Technology Press，2000．（in Chinese）

［8］ 高为炳．变结构控制的理论及设计方法［M］．北京：科学出版社，1996．GAO Wei-bing．Theory and Design Method of Variable Structure Control［M］．Beijing：Science Press，1996．（in Chinese）

［9］ 刘金琨．滑模变结构控制 Matlab仿真［M］．北京：清华大学出版社，2012．LIU Jin-kun．Sliding Mode Variable Structure Control Matlab Simulation［M］．Beijing：Tsinghua University Press，2012．（in Chinese）