初中数学教学中例习题的合理配置

◎福建省漳州第五中学 王奇南 吴 越

初中数学教学中例习题的合理配置

◎福建省漳州第五中学 王奇南 吴 越

在初中数学课堂教学中配置例习题,应本着由浅入深、由易到难、循序渐进的原则，通过一定量的练习，使学生能举一反三，化知识为能力，更好地克服初中数学学习难关．

例习题；配置；教学有效性

数学教学中布置例习题的一个目的，是为了获取学习反馈信息.一方面，通过它反馈学生在掌握知识、巩固知识、应用知识方面的基本情况，以及对所学思想方法的理解与掌握；另一方面，通过它获取学生的理解程度，为后续教学活动的进行打好必要的基础，通过对课后作业的批改，反馈学生对相应知识点的掌握情况.合理的数学例题习题的设置应当贯穿于学生学习活动的全过程，为提高学生数学学习的质量提供最基础的保障，对提高后进生学习数学的积极性和自信心有重要的作用，例习题的合理配置，可成为教学相长的良好信息通道.

我市各类学校使用北师大初中数学教材已经10多年了，笔者在备课、教学与作业批改中遇到许多问题，有很多困惑和思考，以下就这一套教材中例习题的配置情况谈我个人的看法.

一、北师大教材例题习题配置的商榷之处

第一，引入的例题设计不合理，不利于学生由浅入深的掌握知识点.例如分式这一章的第一课时，教材为了引入分式的概念，给的新知引入是文字篇幅占较多的具有实际背景的应用题，这样的例题能够让学生在思考数学的同时紧密联系实际，同时进行环境保护的教育，符合当下新课标的要求，但是对于分式的概念，学生本就不好理解，以这样的形式，无疑是加重了有些薄弱校和农村校孩子的学习难度，无法达到由浅入深带动学生学习的过程.

第二，代数部分例题数量过少.数学运算能力的培养是初中生应具备的一种重要的数学能力，例如教材中因式分解，分式的运算，有理数的运算等几章的内容，如果只用教材中提供的例题，根本达不到学生对新知热身的目的，更不要说举一反三，增强理解，训练学生的解题技巧和能力了.还有一些知识点缺乏例题的支撑，一节课的内容只有探索，没有例题的训练，如果老师在课堂不进行补充训练，学生根本无法掌握和运用所学的知识.

第三，课后习题量少，且跨度太大，层次不明确，学生做起练习困难，容易造成挫败感.教材中的习题编排少，相应的辅助教材又不一定适合我校的生源特点，而多数老师布置家庭作业都是课后习题加上相应的辅助教材，还有一份周末作业.学生完成作业的积极性并不高，较好的学生对作业中的题目，简单的不愿意做，认为自己会做，何必浪费时间；而稍微难的习题就缺乏信心和毅力，懒得动脑，等待老师讲评.较差的学生中存在着作业抄袭、迟交、不交的现象，学生对于完成作业的态度都停留在这是老师布置要检查的任务上，这样就达不到巩固所学知识的目的，还打消了一部分学生学习数学的积极性.

因此，针对这样的情况，探究教材中例题习题如何配置，才能减轻学生的负担，符合学生的发展是很有必要的.

二、初中数学例题习题合理配置的几点建议

1.结合实际，创设例题情境

例题的情境创设得好，容易调动学生的情感、激发学生的创新思维，点燃学生智慧的火花.情境创设要贴近当地学生的生活，让学生利用生活知识感悟数学的内涵，同时也能反映一定的时代气息.例题情境的形式有很多种，如问题情境、故事情境、实验情境、活动情境、竞争情境等.情境的创设要根据学生的实际生活经验而设计.对于初中生，更需要紧密联系学生的生活环境，创设有助于学生自主学习、合作交流的例题背景，用生活中的数学魅力去吸引学生.

例如，北师大版七年级《探索三角形全等》第一课时中，整节课的教学内容以探索为主线，学生在探索过程中得出“SSS”可以判定两个三角形全等的结论，但教材因为篇幅有限，探索较少，缺乏例题让学生及时对所学定理加以巩固应用，所以教师可以根据当地的具体情况创设这样的例题情境：

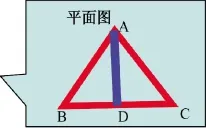
例1.如图，是2001年建成的漳州战备大桥，采用了塔梁固结、塔墩分离的结构体系. ΔABC是钢绳和桥身的一部分构成，钢绳AB=AC，AD是连接点A与BC中点D的塔梁，请问：ΔABD和ΔACD全等吗？说明理由.

2.层次分明，灵活改编例题

例题是教学内容的一个重要环节，好的例题能激活思维能力层次不同的学生.针对教材和现有学生实际，教师要精选设计课堂例题，例题的选择要难易适中，有弹性，数量不宜过多也不能过少，要让学困生巩固基础知识，中等生强化基本技能，学优生优化知识结构.

例如，北师大版七年级《合并同类项》第二课时中，要求学生准确找到同类项，经历合并同类项的过程，掌握合并同类项的思想方法.这一课时的教材中例题共有5题，课堂习题4题，课后练习10题，在数量上符合学生掌握知识的需求，但对于学习能力不佳的学生，我认为教师在例题的安排上可以适当的分层次，将书本中的例题适当改编为：

例1.根据乘法分配律合并同类项

（1）3a+2a-10a；（2）-xy2+3xy2.

例1是可以直接进行合并同类项的，为了让学困生巩固基础知识，掌握合并同类项就是把同类项的系数相加，字母和字母的指数不变的原理.

例2.合并同类项

（1）3a+2b-5a-b；（2）7a+3b2+2a-a2+3；

（3）-4ab+8-2b2-9ab-8.

例2比例1稍微难了一点，需要学生先找出同类项，是同类项的先做上相同的记号，然后再根据记号，将同类项放进同一个括号里，再用例1的方法合并同类项，这样学生就将合并同类项的法则再巩固一遍了.

例3.求代数式的值

（1）-3x2+5x-2x2+x-1，其中x=2.

例3是书本上的做一做，根据学生的实际情况，把其中一个小数系数换成整数系数，降低了学生计算的难度.

根据这节课的教学内容和初一新生学生的认识结构水平，在教学时不急于将学生拔高，应先易后难，由浅入深的原则设计例题，使教学循序渐进，从而使学生更好的掌握知识，这样才不会出现“尖子生吃不饱，英雄无用武之地；差生消化不良，感到非能力所及”.

3.目的明确，有效配置习题

习题要避免繁琐、机械、重复，忌题海战术.学生从小学刚升入初中，由于教学内容增多，教师教学方式、学习环境等发生变化，如果习题内容重复，会使学生厌烦，形成要数量不要质量的心态，达不到巩固知识的目的，失去习题的有效性，反而使学生厌烦数学这门重要的基础学科.在减少习题量的同时，教师应当增加习题的深度和广度，给学生一个更广阔的平台.

为了让习题的设置能够有效，教研组可以根据学校的生源特点进行校本习题的开发，这样的习题对该校学生是具有一定针对性的，可以将习题的结构大致分为基础训练、能力提升两部分.校本习题的制定需要经过选材、编制、使用、修订、建库五步奏，经过这五步奏选出的习题才具有有效性，才能去粗取精.

例如《因式分解——平方差公式》这一课时的习题可以这样配置

一、基础训练

1.（a+b）（a-b）= ；反过来：a2-b2=（ ）（ ）.

2.分解下列因式:

（3）x2-18=x2-2=（ ）（ ）；

（2）16-x2=2-x2=（ ）（ ）；

（3）x2-25y2=2-x2=（ ）（ ）；

（4）9x2-25y2=（ ）2-（）2=（ ）（ ）.

3.若a+b=1，a-b=2，则a2-b2= ；

若a2-b2=1，a+b=0.5，则a-b= .

4.下列各式中可以用平方差公式分解因式的是（ ）

A.a2+（-b）2B.4x2-2y C.9m2-n2D.a2-2a+1

5.分解下列因式:

（1）1-36b2；（2）049p2-144；（3）12x2-3y2；

（4）x4-81；（5）-5a3b+20ab3；（6）（x+y）2-（x-y）2；

（7）a2-b2+a-b；（8）4（a+b）2-9（a-b）2.

基础训练中的1、2两小题是针对平方差公式在因式分解中的简单技能训练，多数学生能掌握，可以达到夯实基础的作用；3、4、5三小题的设置除了夯实基础，还要求学生学会灵活运用公式，在计算解题中注意格式的书写，以及渗透了整体的思想，总之，基础训练更重要的是让学生产生学习的成就感，感到能力能及，激发学生的学习动力.

二、能力提升

6.用适当的方法计算：

（1）19.52-0.52； （2）23×1012-992×23.

7.分解下列因式：

（1）x2（a-1）+y2（1-a）； （2）3（a+b）2-27c2.

8.如图,在半径为R的圆形钢板上，冲去半径为r的四个小圆，计算当R=7.8cm，r=1.1cm时剩余部分的面积（π取3.14）.

在配置习题时，我们不应急于将学生拔高，应先易后难，由浅入深的原则设计习题，即先基础训练，再能力提升，从而使学生更好的掌握知识.

4.大胆拓展，完善习题配置

美国著名教育学家布鲁斯说：“教学生任何科目，决不是对学生灌输固定的知识，而是启发学生主动地去获取和组织知识”.除了配置基础训练和能力提升之外，可以再配置1至2道拓展提高的题型供班级部分学生训练，例如，拓展提高《因式分解——平方差公式》这一课时的习题，如下：

1.正数a，b，c是三角形的三边长，且有（a2-c2）+（ab-bc）成立，则这个三角形是 三角形.

2.对于任意的自然数n，（n+7）2-（n-5）2能被24整除吗?为什么?

值得一提的是拓展提高的配置应是在学生学习的知识生长点上加以拓展和延伸，并不是越难越好，要体现让学生“跳一跳，摘桃子”，让他们体验成功的喜悦.

又比如，我们可以在重点章学完后，让学生出一份数学手抄报作为复习笔记.要求去体现这一章的重难点，出的试题要覆盖每小节，还可以联系自己的实际学习情况，找出易错题示例、一题多解等.出报以小组4人为一组，优等生与薄弱生搭配的方式.通过几次的手抄报编写，在优生的带动帮助下，大多数学生的主体意识得到增强，知识得到巩固和拓展.再讲成果贴到学生栏里，接受大家共同的改进，这样的作业学生做得开心，且有收获，使学生的创新思维更符合实际，把创新思维的成果物化，让学生体会到创新的乐趣.

《义务教育数学课程标准（2011年版）》指出：义务教育阶段的数学课程标准应该体现基础性、普及性和发展性，使数学教育面向全体学生，实现人人学有价值的数学，人人都能获得必需的数学，不同的人在数学上得到不同的发展.合理配置和设计例题习题，应充分体现新课程以人为本的概念，调动学生的兴趣和激活学生的创新意识.合理配置例题习题，秩序渐进、逐步加深正是体现了新课标提出的基础性、普及性和发展性要求，教学实践表明：合理配置例题习题，可以降低学生学习难度，增强学生学习信心，培养学生学习兴趣，使班级学生数学作业的完成率和正确率得到较大提高.

（责任编辑：王钦敏）