基于MATLAB的数字电视图像处理的矩阵表示及正交变换

山东广电网络有限公司潍坊分公司 王晓东

基于MATLAB的数字电视图像处理的矩阵表示及正交变换

山东广电网络有限公司潍坊分公司 王晓东

MATLAB语言是功能很强大的数据分析软件,它提供了效率很高的信号处理工具，本文介绍了如何利用MATLAB图像工具箱来实现矩阵表示和正交变换。

数字图像处理；MATLAB；快速傅立叶变换(FFT)

1 图像的矩阵表示及正交变换

1.1 图像的矩阵和向量表示

二维图像进行均匀取样，可得出一幅离散化成M×N样本的数字图像，它是一个整数阵列，因而用矩阵来描述该数字图像是最简洁和直观的。

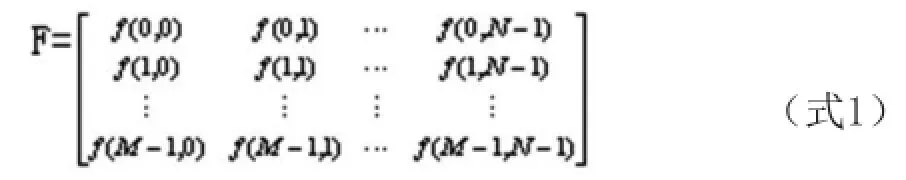
其中，f(i,j)表示(i,j)位置处的亮度量化值。

数字图像的向量表示形式为：

将图像数据矩阵按行的顺序转换成向量形式：

MATLAB在处理图像时，都是以数组、向量、矩阵的样式来表示图像，进行各种运算。

1.2 图像的分析方法及正交变换

对图像的处理一般都是通过数学的方法进行处理的，现简单介绍一下小波分析法。

1．2．1 小波分析法

小波分析在图像处理中应用广泛，价值极高。主要用于分析基于小波分析的图像平滑、融合、增强和压缩技术,并运用Matlab软件进行模拟,对得出的结果进行分析。

这里，R*=R-{0}表示非零实数全体，对于任意的函数或者信号f(x),其小波变换定义为：

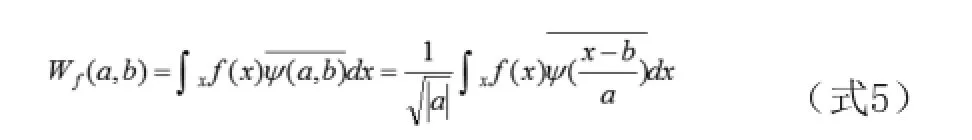
因此，对任意的函数f(x)，它的小波变换是二元函数。

1．2．2 基于DCT变换的频域变换

基于DCT变换的数字水印算法的原理如下：

将一个图像分为M×N大小的子块，则可以对每一子块进行离散余弦变换，得到M×N大小的系数矩阵，其变换公式为：

其中，u,v=0,1,2,…N-1;当u=v=0时,E[u]=E[v]=1/；其余，E[u]=E[v]=1；

将变化后的系数矩阵使用DCT逆变换还原为水印化图像，公式如下：

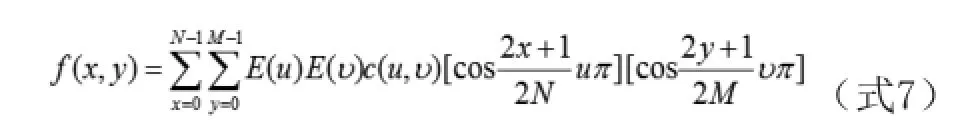
其中，u,v=0,1,2,…N-1；当u=v=0时，E[u]=E[v]=1/；其余，E[u]=E[v]=1；

1．2．3 一维离散傅立叶变换(DFT)

设f(x)为输入离散序列，F(u)为f(x)的离散傅立叶变换,则正变换为：

反变换为：

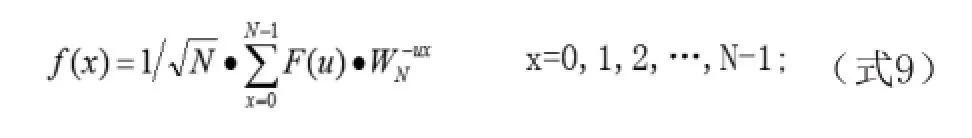
1．2．4 二维快速傅立叶变换(FFT)

定义二维DFT，设f(x,y)是二维离散输入数据，F(u,v)为f(x,y)的二维离散傅立叶变换,则正变换：

u=0,1,2,…,M-1;v=0,1,2,…,N-1;

反变换：

x=0,1,2,…,M-1;y=0,1,2,…,N-1;

2 图像预处理

2.1 图像增强

针对图像字符分辨不清，甚至无法定位和分割，更无法识别的情况，我们采用了一下几种有效增强图像对比度的方法。

2．1．1 灰度校正

实验中发现总体上灰度值偏低，图像不明亮且发暗。根据图像处理系统的条件，将灰度范围安排到s=(0,255)之间。我们对灰度值作如下的线性变换：

使得s属于[smin,smax]，其中，T为线性变换，

若r(50,150)、s(0,255)，则：

2．1．2 平滑处理

受干扰而图像质量降低的图像的处理，我们主要采用图像平滑处理，经常使用的方法有：多帧平均法，结构性噪声消除，局部平均法等。

图像在经过二维傅立叶变换后，空间高频分量中就含有了噪声。因此，对高频成分进行衰减就可以在频域中实现对图像的平滑处理。这种保留低频成分且滤除高频成分的方法，我们称之低通滤波法。常用的低通滤波器有四种，他们都是零相移滤波器，而对频率平面的原点是圆对称。

2.2 图像的二值化

在识别前首先将图像二值化，是为了便于以后的识别。对图像进行二值化处理，可以方便以后的分割识别工作。常用的二值化方法有动态门限法、松弛法、抖动矩阵二值化法、直方图统计法等。其中全局门限法很简单也很实用，具体是根据输入图像的灰度直方图的分布，确定目标与背景的分离界限。

2.3 图像锐化

图像经过转换或传输后，图像的质量可能会下降，可能会产生模糊现象。此时，我们需要用到图像锐化技术；图像锐化是一种对图像轮廓进行补偿的处理方法。图像锐化有两大类，分频域处理和时域处理。

2．3．1 高通加强滤波器

为了加强空间高频分量，我们采用高通加强滤波器。高通加强滤波器相对突出高频成分，相对抑制低频成分和甚高频分量，我们可以把它看成是由三种滤波器组成的。

2.3.2 微分法

在(x,y)点的梯度，其方向是函数在这点变化率最大的方向，其长度为函数f(x,y)的最大变化率：

(3)反锐化掩模法，其基本算法如下：

应用MATLAB图像处理工具，成功实现了数字电视图像处理的矩阵表示及正交变换，为下一步的数字处理与操作提供了基础。

王晓东（1985—），男，山东临朐人，大学本科，广播电视助理工程师，就职于山东广电网络有限公司潍坊分公司。