船舶肘板拓扑优化设计
2015-02-07程远胜刘甜甜刘均
程远胜,刘甜甜,刘均
华中科技大学船舶与海洋工程学院,湖北武汉430074
0 引 言
组成船体纵向或横向框架的构件常采用三角形肘板连接。现代船舶的建造运营表明,肘板的损伤与裂纹的出现大量存在着,其中肘板损伤数约占整个结构损伤数的26.85%[1]。这些损伤主要由肘板处的应力集中引起,因此,提出新的肘板结构型式,对有效降低节点结构的应力集中程度具有较大的实用价值。
Kim 等[2]对船舶肘板的材料进行了研究和探索,设计出了一种高强度的低碳素铸钢,其屈服极限和极限拉伸强度分别为480 和600 MPa,在保证应力集中不恶化的情况下,肘板尺寸和重量分别下降了30%和50%。郭信川等[3]提出了基于修改的粒子群算法的船舶肘板优化方法,对肘板节点结构进行了形状优化,最终优化后的新型肘板节点结构较原始肘板节点结构的应力集中程度降低了10.03%。Lim 等[4]研究了肘板对框架接头处应力分布和极限强度的影响,其根据节点的力学特性,重新设计了肘板的形状,有效改善了其结构应力状态。姜以威等[5]研究了梁肘板的应力集中,认为它是由梁肘板节点的内部特性和外部输入特性所引起,并分析了梁肘板的焊接工艺性、节点形式和尺寸对应力集中的影响。王波和杨平[6]针对船体的梁连接节点,在ANSYS 中建立了梁连接节点的壳单元模型,探讨了肘板尺寸变化对节点承载能力的影响规律,并对比了几种常见节点的强度和屈曲性能。史战新[7]也针对肘板的优化做了一定的工作,其针对水下结构物的肘板结构,基于子模型法分析了节点的结构应力,并在此基础上应用ANSYS 与Matlab 的联合双目标遗传算法对其进行了形状优化,优化后的肘板结构疲劳寿命得到了很大的改善。田旭军等[8]通过ANSYS软件和改进的遗传算法,对水下结构物的肘板结构进行形状优化设计,降低了肘板节点的应力集中。
本文将提出船舶典型节点肘板的拓扑优化设计数学模型,基于Optistruct 软件进行肘板拓扑优化设计,并将获得的肘板拓扑优化设计结果进行适当的工程化处理,以有效降低节点结构的应力集中程度。
1 船舶肘板节点结构应力分析
1.1 整体模型强度计算
选取某船舶三舱段结构作为分析对象,其典型特征是中间舱段第1 层、第2 层的甲板设有大开口,其横截面如图1所示。三舱段结构总长L=30 m,宽B=18.36 m,型深D=11.3 m,大开口宽度9.12 m,第1 层(顶层)甲板结构布置如图2 所示。结构材料弹性模量E=200 GPa,泊松比μ=0.3,材料密度ρ=7 800 kg/m3。
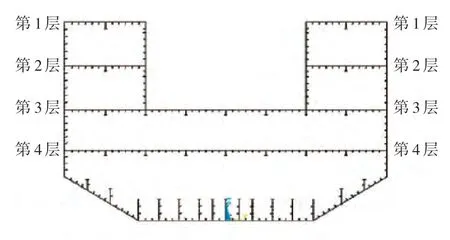
图1 舱段结构横截面示意图Fig.1 The cross-section of the middle cabin structure
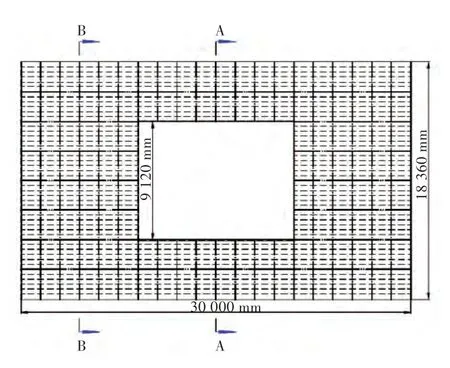
图2 第1 层甲板结构布置图Fig.2 The structural layout plan of the first deck
子模型区域为连接船舶舱壁垂直桁材与第2层甲板纵桁的肘板节点结构。大开口舱段的有限元模型不含肘板结构。甲板板、舷侧外板、外底板、肋板、龙骨以及甲板桁材腹板采用板壳单元Shell 181 模拟,子模型区域外的甲板纵骨、甲板桁材面板和舷侧纵骨等采用梁单元Beam 188 模拟,而子模型区域内的这些结构则全部采用板壳单元Shell 181 模拟。有限元整体模型如图3 所示。共划分有188 599 个单元,其中板壳单元135 659 个。

图3 三舱段结构有限元整体模型Fig.3 The FEM model of a three-cabin structure
有限元模型全局坐标系为直角坐标系,船长方向向艏为X 轴正方向,船宽方向向左为Y 轴正方向,型深方向向上为Z 轴正方向。为了模拟大开口舱段真实的受力状态,在舱段两端建立刚性域并在两端形心处加载463 094.4 kN·m 的弯矩,在第1 层甲板表面加载4.9 kPa 的均布压力,在第2,3,4 层甲板上加载9.8 kPa 的均布压力。边界条件为:在舱段一端的主节点约束其所有平动自由度和X,Z 方向的转动自由度,释放Y 方向的转动自由度;另一端的主节点约束其Y,Z 方向的平动自由度以及X,Z 方向的转动自由度,释放X 方向的平动和Y 方向的转动。整体模型计算结果如图4 和图5 所示。
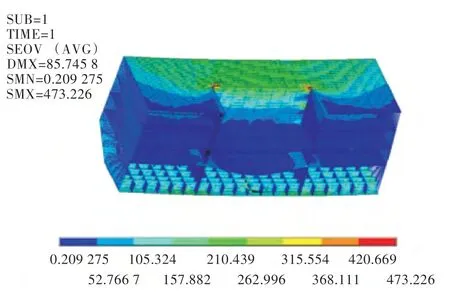
图4 整体模型应力云图Fig.4 Mises stress contours of full model
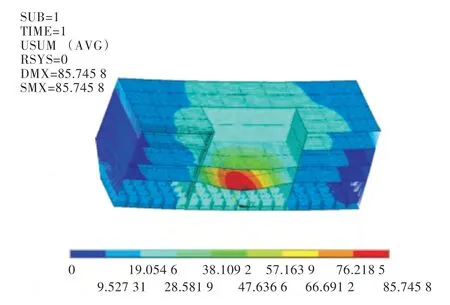
图5 整体模型变形云图Fig.5 Displacement contours of full model
1.2 子模型应力计算
1.2.1 强度计算的有限元子模型
本文采用子模型法对肘板节点结构进行应力分析。子模型法基于圣维南原理,即如果实际分布载荷被等效载荷代替,应力和应变只在载荷施加位置附近有改变。因此,只要子模型切割边界避开载荷集中及应力集中位置,子模型内部就可以得到较精确的解[9]。在应力的精细化分析中,子模型法得到了广泛应用[10-11]。
本文在ANSYS 和Hyperworks 软件中建立有限元子模型的步骤如下:
1)在ANSYS 中生成并分析较粗糙网格的整体模型,保留整体模型.db 文件及结果.rst文件;
2)在ANSYS 中生成子模型的几何模型,在关注区域添加肘板结构,将几何模型文件导入Hyperworks 并划分细网格,生成节点;
3)将在Hyperworks 软件中生成的肘板节点结构的有限元子模型导入ANSYS 中,提取并保存子模型边界节点,以及后缀为.node 的文件,默认文件名与子模型文件名一致;
4)在ANSYS 子模型工作环境下恢复整体模型.db 文件,在后处理模块读入整体模型结果文件,利用命令“cbdof”形成后缀为.cbdo 的子模型边界插值文件;
5)在ANSYS 软件中恢复子模型.db 文件,在求解模块读入上一步生成的.cbdo 文件,并根据子模型范围内的实际位移边界条件及外载荷进行加载求解。
子模型的切割边界需远离关注区域,边界的选取也要经过尝试验证后才能确定。根据整体模型的应力分布,初步选取Z 方向范围为(6 580~11 300),X 方向范围为(-6 000~7 250),Y 方向范围为(-950~950),其在全局坐标系下的位置、材料参数以及单元类型等均与整体模型中一致。
在子模型的其他部分,采用20 mm 的网格进行划分,并在肘板关注区域以5 mm 的网格进行划分。关注区域为舱壁垂直桁材与第2 层甲板纵桁连接处,如图6 所示。加载插值边界及子模型区域内其他载荷后的子模型有限元模型如图7所示。
完成边界条件的切割、插值以及对子模型的分析后,应首先验证切割的边界是否离应力集中区域足够远。本文对比了子模型的切割边界处和整体模型对应位置的Mises 应力,发现两者的应力分布与大小基本一致,认为子模型的边界选取较合适。
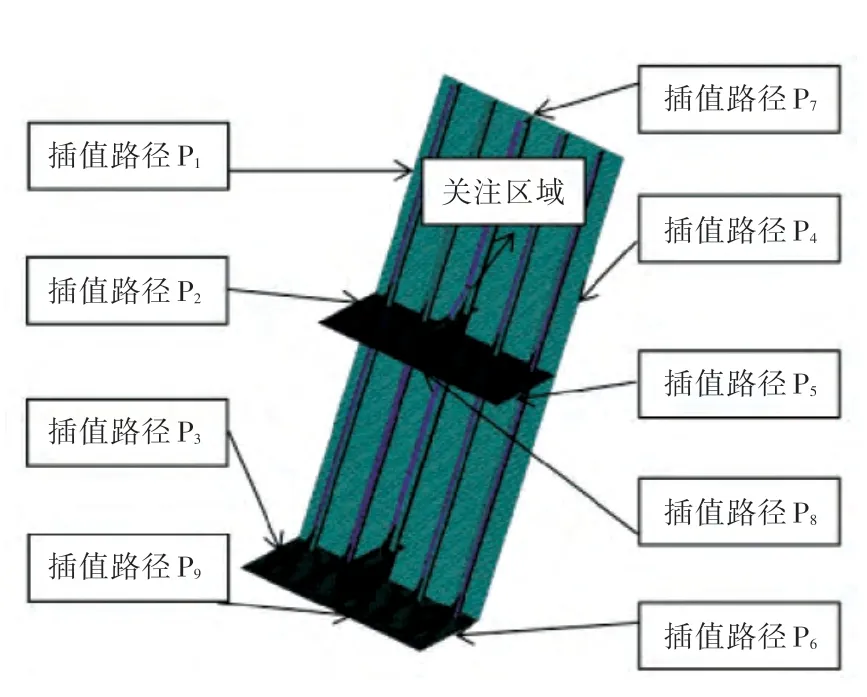
图6 肘板节点结构子模型Fig.6 FE model of sub-model
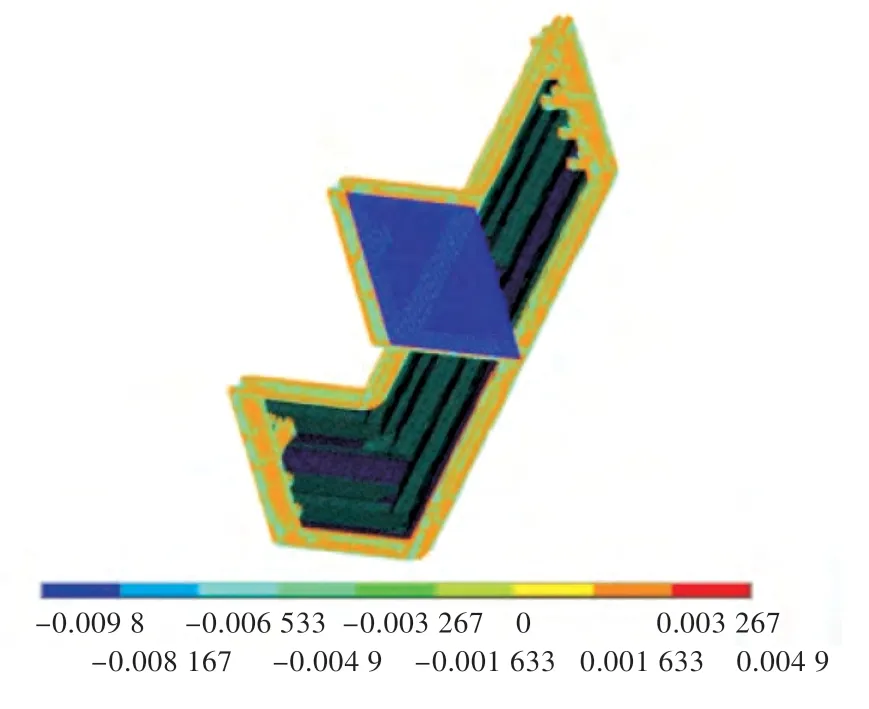
图7 子模型边界插值及其加载Fig.7 Boundary interpolation and loading of sub-model
1.2.2 典型节点结构子模型法计算结果分析
本文关注的节点为连接船舶舱壁垂直桁材与第2 层甲板纵桁的肘板节点,如图8 所示。为便于表述,图中桁材面板的浅色区域称为区域2,桁材腹板的浅色区域称为区域3。
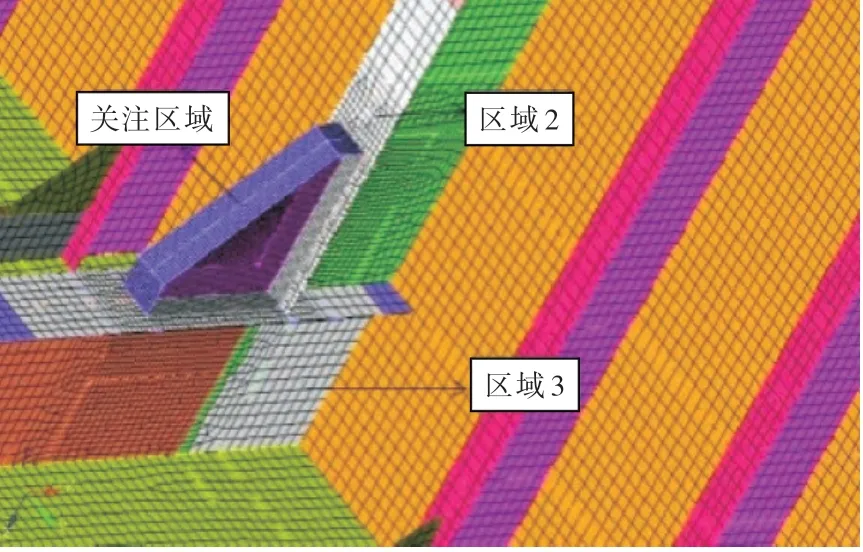
图8 拓扑优化对象初始形状Fig.8 Original structure of bracket
应用子模型法计算该处有肘板和无肘板情况下的应力分布,计算结果如图9 所示。在有肘板的情况下,区域2 的最大Mises 应力为145.0 MPa,出现在肘板与舱壁桁材面板的连接处;区域3 的最大Mises 应力为72.39 MPa,出现在区域3 的中心处;肘板区域的最大Mises 应力为260.30 MPa,出现在肘板与第2 层甲板纵桁面板的交汇处。在无肘板的情况下,区域2 的最大Mises 应力为207.20 MPa,出现在两桁材面板的连接处;区域3的最大Mises 应力为83.52 MPa,出现在区域3 的中心处。由此可知,肘板的存在极大地改善了区域2 的应力集中,但是在肘板的角趾处产生了新的应力集中点。
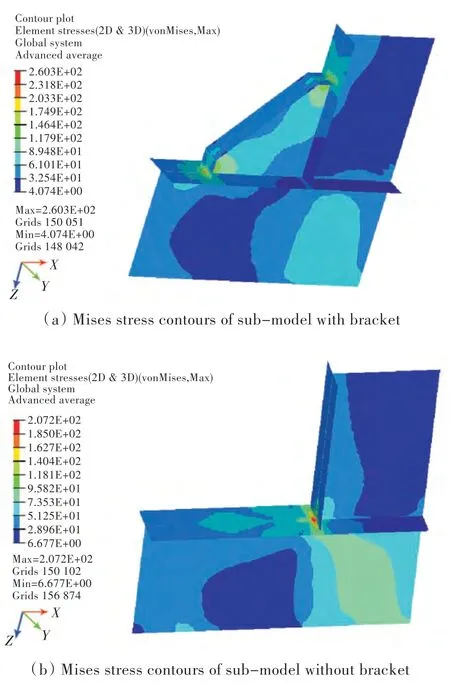
图9 有、无肘板应力分布结果Fig.9 Mises stress contours of sub-model with and without bracket
2 船舶肘板节点结构的拓扑优化
2.1 拓扑优化数学模型
本文基于Optistruct 软件,采用变密度法对船舶肘板节点结构进行拓扑优化。所谓变密度法[12],其实是一种伪密度法,即人为假设的一种材料物理参数(如弹性模量)与密度之间的一种线性或者非线性关系,经过拓扑优化后的单元密度一般按照0~1 分布在给定的初始拓扑优化区域上。通过控制单元的密度向0 或者1 两端收敛,可以使得拓扑优化结果抽象成可以加工的结构。
本文的优化对象为图8 中所示的肘板,设计变量为肘板结构的单元密度。肘板优化设计的首要目标是降低区域2 的应力集中。由于Optistruct软件在进行优化求解的过程中不能提取设置为设计变量区域结构的应力,但鉴于区域2 的应力水平与肘板自身的应力水平具有一定的对应关系,所以将区域2 的Mises 应力最小化来作为优化目标。为保证桁材的抗弯强度,约束函数设定为区域2 的Mises 应力。在有肘板的情况下,区域3 的最大Mises 应力为72.39 MPa,在无肘板的情况下,区域3 的最大Mises 应力为83.52 MPa,因此,为保证桁材的抗弯强度,本文在进行肘板优化设计时限定区域3 的Mises 应力不得大于73 MPa。
2.2 拓扑优化结果及工程化处理
求解上述数学模型,至优化迭代20 步时停止计算。为便于观察,隐藏非设计区域单元,只显示设计区域单元,优化后,节点结构的密度云图如图10 所示。目标函数随迭代步数的变化历程曲线如图11 所示,图中,横坐标为迭代步数,纵坐标为目标函数的数值。由图11 可以看出,最后的目标函数已经收敛,说明肘板的优化在该数学模型下已经达到最优。
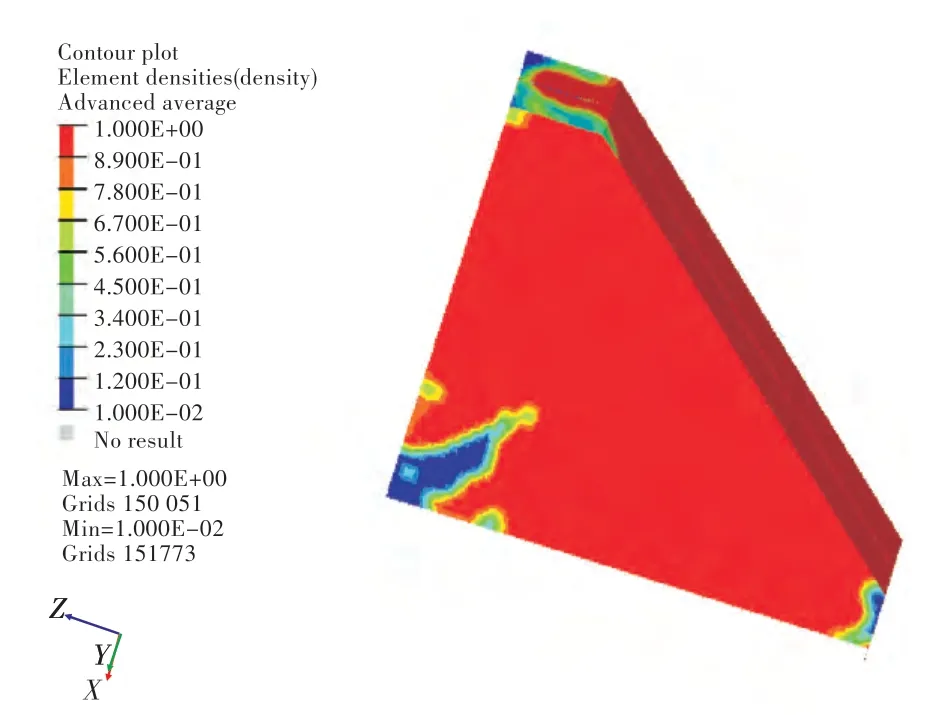
图10 肘板拓扑优化密度云图Fig.10 Density contours of topology optimization
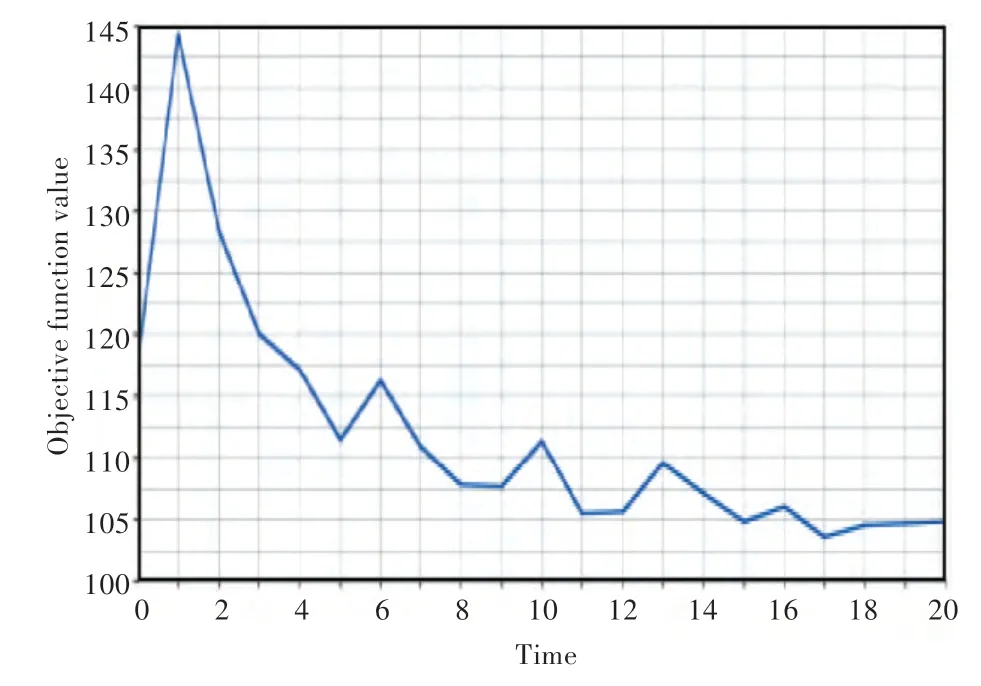
图11 目标函数迭代历程曲线Fig.11 Objective function--time process of topology optimization
肘板最后一步迭代的应力云图如图12 所示。肘板自身最大Mises 应力随迭代步数的变化历程曲线如图13 所示,图中,横坐标为迭代步数,纵坐标为肘板的最大Mises 应力。
对应于优化的最终迭代步数,肘板区域的最大Mises 应力为194.20 MPa,区域3 的最大Mises应力为72.66 MPa,区域2 的最大Mises 应力为102.98 MPa。密度云图中,越接近红色(深色部分),就表示这部分的材料越重要,越接近蓝色(浅色部分),就表示这部分的材料越可以舍弃。综合以上结果,可以对肘板的拓扑优化结果进行定性分析,认为肘板的3 个尖角是引起桁材面板和肘板自身应力集中的主要因素。
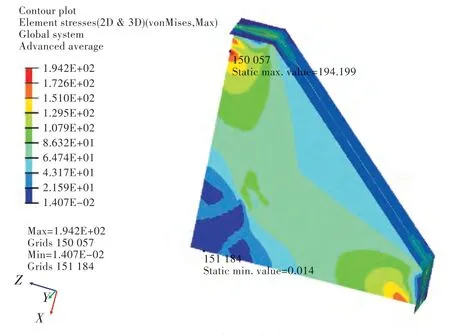
图12 拓扑优化应力云图Fig.12 Mises stress contours of topology optimization
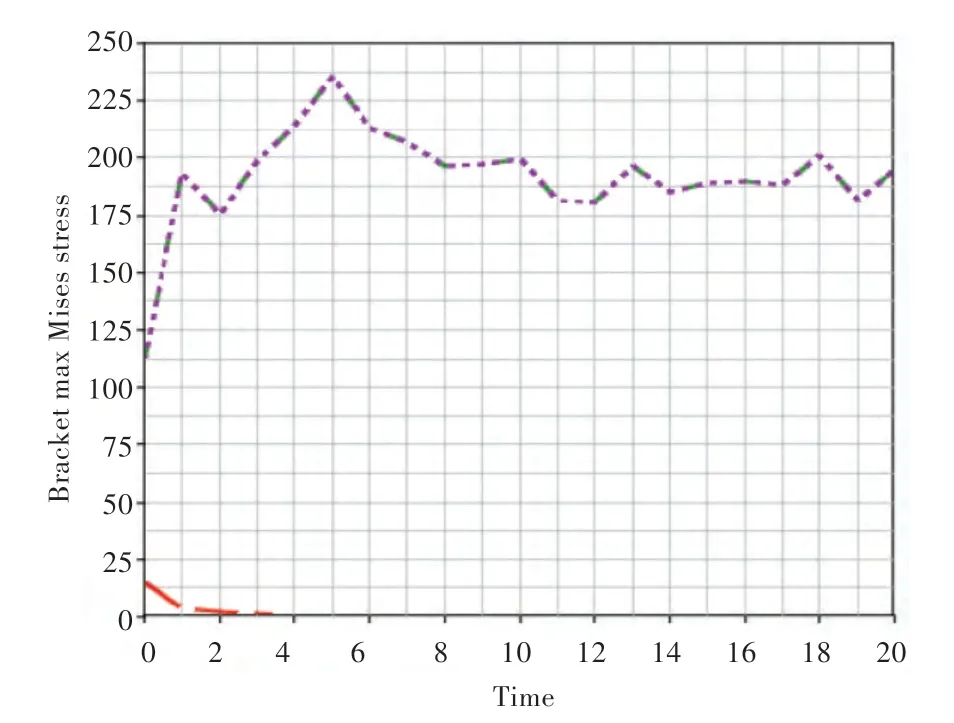
图13 肘板应力迭代历程曲线Fig.13 Bracket stress--time process of topology optimization
根据图10 所示的肘板拓扑优化结果及分析,对肘板结构进行了如下工程化处理,并在肘板的3 个尖角处设置了相同半径的圆弧开口,如图14所示。采用前述的子模型分析法,分别对圆弧半径取10~46 mm 的方案进行肘板节点结构应力计算。
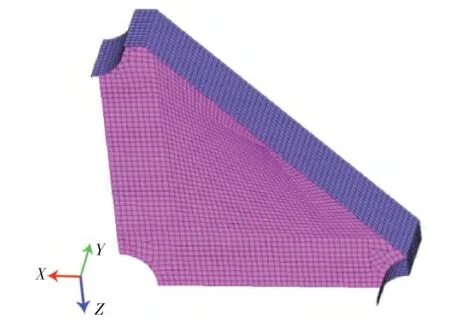
图14 修改后的肘板结构型式Fig.14 New bracket structure type
应用上述子模型法对不同圆弧半径的肘板进行计算,结果如表1 所示。在计算过程中,为避免网格划分对结果的影响,模型的网格密度、网格质量以及网格参数等均保持一致。
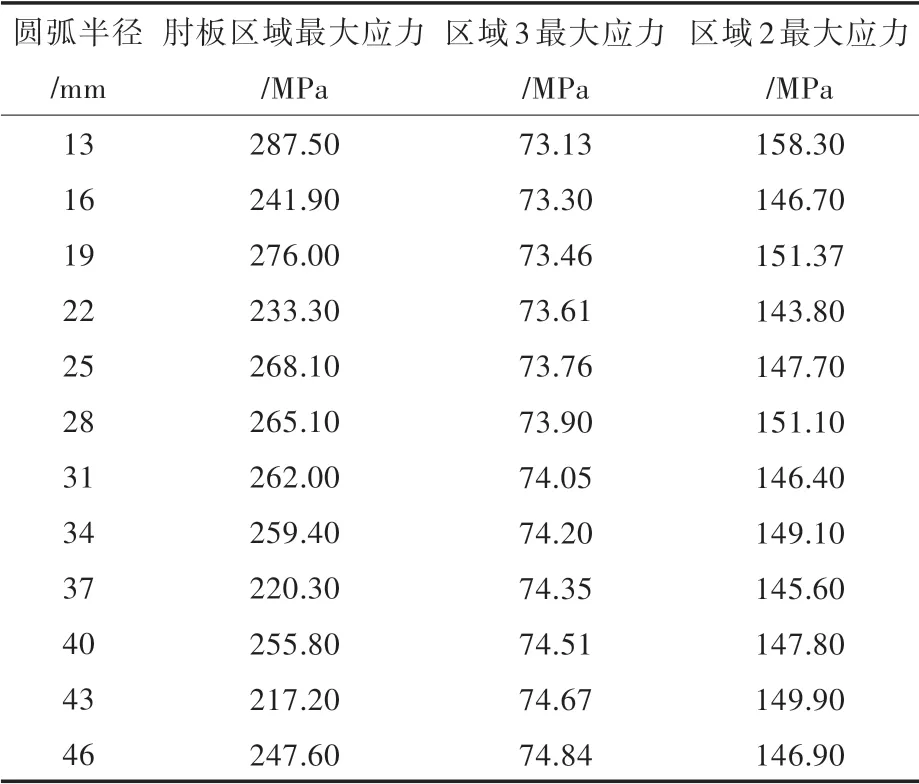
表1 不同圆弧半径时应力结果Tab.1 Mises stress results of model with different radii
表1 的结果表明,当圆弧半径较大时,在保证区域2 和区域3 的应力水平变化不大的情况下,肘板自身的应力水平与传统的三角形肘板相比有所下降。当圆弧半径为43 mm 时,对肘板自身的应力降低效果最好,和传统的三角形肘板相比,应力降低了16.56%。
3 结 论
本文通过引入子模型技术,对船舶肘板节点结构进行了应力精细化分析,并在此基础上,以肘板结构的密度为优化变量,以与肘板相连的桁材面板的Mises 应力为目标,以与肘板相连的桁材腹板的Mises 应力为约束条件,建立了合理的拓扑优化数学模型并进行了肘板优化设计,在根据肘板拓扑优化结果进行适当的工程化处理后,提出了一种新型的肘板结构型式,得到如下结论:
1)肘板的存在较好地改善了桁材面板交汇处的应力集中。对于本文的算例,桁材面板交汇处的最大Mises 应力由207.2 MPa 降低到了145.0 MPa,降低了30.02%。但肘板的存在又引起了新的应力集中点,肘板与桁材面板交汇处的应力达到了260.30 MPa。
2)基于肘板拓扑优化结果提出的新型肘板结构型式是一种在传统三角形肘板的3 个尖角处设置1/4 圆弧的结构。该种肘板在本文所采用的典型载荷下有效降低了节点结构的应力集中。对于本文的算例,肘板与桁材面板交汇处的应力由260.30 MPa 降低到了217.20 MPa,降低了16.56%。所提出的肘板结构拓扑优化设计方法为获得创新性的肘板结构型式提供了一种新的手段与方法。
[1]JORDAN C R,COCHRAN C S. In service performance of structural details:SSC-272[R].Ship Structure Com⁃mittee,US,1978:154-159.
[2]KIM T W,LIM S S,SEOK H H,et al. Concurrent engi⁃neering solution for the design of ship and offshore bracket parts and fabrication process[J]. International Journal of Naval Architecture and Ocean Engineering,2013,5(3):376-391.
[3]郭信川,吳俊仁,陳慶忠. 艙口圍緣之鍵槽端肘板構件最佳化之研究[J]. 中國造船暨輪機工程學刊,2009,8(3):131-142.KUO H C,WU J L,CHEN C J. Optimization design of a match-stick-hole end-bracket device of a hatch[J].Journal of Taiwan Society of Naval Architects and Ma⁃rine Engineers,2009,8(3):131-142.
[4]LIM J B P,NETHERCOT D A. Design and develop⁃ment of a general cold-formed steel portal framing sys⁃tem[J]. The Structural Engineer,2002,80(21):31-40.
[5]姜以威,王广戈.梁肘板节点的应力集中研究[J].镇江船舶学院学报,1990,4(4):47-56.
[6]王波,杨平.船舶结构节点的承载力分析[J].船海工程,2010,39(2):18-21.WANG Bo,YANG Ping. Analysis of the load bearing capacity of ship structural details[J]. Ship and Ocean Engineering,2010,39(2):18-21.
[7]史战新.基于Ansys 子模型法的肘板结构优化[J].舰船科学技术,2014,36(8):19-26.SHI Zhanxin. The bracket structure optimization based on Ansys sub-model method[J]. Ship Science and Technology,2014,36(8):19-26.
[8]田旭军,闫国强,胡刚义. 基于遗传算法的肘板结构型式优化[J].中国舰船研究,2007,2(2):23-26.TIAN Xujun,YAN Guoqiang,HU Gangyi. Optimiza⁃tion of bracket plate using genetic algorithm[J]. Chi⁃nese Journal of Ship Research,2007,2(2):23-26.
[9]夏伟,胡成,瞿尔仁.Ansys 子模型分析技术在处理应力集中时的应用[J]. 工程与建设,2006,20(2):92-94.XIA Wei,HU Cheng,QU Erren. Applications of Ansys submodeling technology in dealing with stress concen⁃tration[J]. Engineering and Construction,2006,20(2):92-94.
[10]朱扬,程远胜,刘均.激光焊接夹层甲板板格强度计算的子模型方法[J]. 船舶力学,2014,18(10):1228-1236.ZHU Yang,CHENG Yuansheng,LIU Jun. Sub-model method for strength calculation of a laser-welded steel sandwich panel structure[J].Journal of Ship Me⁃chanics,2014,18(10):1228-1236.
[11]王虎,程远胜,刘均. I 型金属夹层结构连接构件强度数值计算方法[J]. 中国舰船研究,2012,7(3):51-56.WANG Hu,CHENG Yuansheng,LIU Jun. Strength analysis on model I-core steel sandwich panel joints[J]. Chinese Journal of Ship Research,2012,7(3):51-56.
[12]朱剑锋,林逸,陈潇凯,等. 汽车变速箱壳体结构拓扑优化设计[J]. 吉林大学学报(工学版),2013,43(3):584-589.ZHU Jianfeng,LIN Yi,CHEN Xiaokai,et al. Struc⁃tural topology optimization based design of automotive transmission housing structure[J]. Journal of Jilin University(Engineering and Technology Edition),2013,43(3):584-589.
