复杂目标散射均值预估方法
2015-02-06向前方重华熊波刘义
向前,方重华,熊波,刘义
(1.海军驻武汉七〇一所军事代表室,武汉 430064;2.电磁兼容性重点实验室中国舰船研究设计中心,武汉 430064)
自从雷达问世以来,复杂目标(尤其是舰船目标)的雷达散射特性一直是研究的热点。多年来,这一领域的研究重点是远场分析:假设入射波为平面波,计算其散射远场,评估其雷达散射截面(RCS)。
许多研究中因雷达与目标的间距不够远,无法将入射波近似为平面波。此时,远场散射分析条件无法满足,使用近场散射分析方法则更为有效。因此,在一定条件下,开展目标近场散射特性研究更为重要,例如舰船目标,大多数情况下都处于探测的近场区。
有关近场散射研究的文献资料较少,主要有DEMACO开发的NcPTD和Cpatch代码可以处理近场散射[1]。Shyh-Kang Jeng基于PTD和SBR也开展了近场散射研究[2],但这些研究主要基于高频方法而非数值方法。由于数值分析方法MLFMM的预测精度高于高频方法,较高的精度能够确保特性分析的有效性,且文献资料中尚未见基于MLFMM的舰船目标近场散射分析研究。此外,有关远场距离条件的讨论一直存在。其中,Kouyoumjian and Peters在1965年就对这一表达式的关键参数进行过探讨,E.F.Knott and T.B.A.Senior在1974年也曾经对某些典型二维目标的的远场距离条件开展研究。在1999年,Rajeev Bansal在其论文中综述了远场距离条件的多种表现形式,然而文献中可见的研究工作主要针对峰值而非均值。
文中基于MLFMM方法给出了某舰船模型的近场散射结果,及其随探测距离、频率和方位角的变化曲线。此外,还对不同探测距离条件下舰船散射均值进行比较,并提出针对散射特性均值结果的定量预估均值分析方法。
1 散射特性分析方法
以某简化舰船模型在自由空间条件下的近场散射问题为例,如图1所示。使用MLFMM方法[3]对舰船的电磁散射场进行计算,将舰船表面分解为N个三角形面元,从而使每个面元都处于自身的远场区,由电场积分方程对散射场进行求解:


图1 某简化舰船模型(34 m×7 m×8 m)Fig.1 The simplified ship model(length 34 m×width 7 m×height 8 m)
传统的远场散射(即RCS)表达式为:
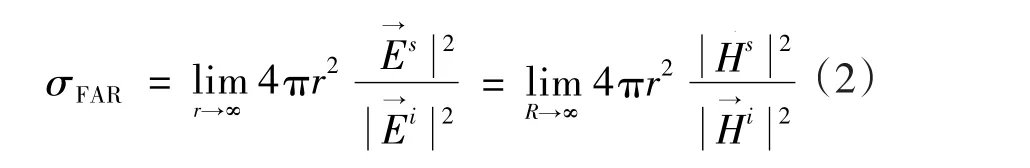
远场RCS参量预测需保证入射到舰船表面的波前为平面波。在近场区,则需采用球面波前来近似考虑天线的方向性影响,假设天线是各向同性的,则近场散射表达式为:

2 计算结果与分析
自由空间中典型简化舰船的近场和远场散射特性的差值曲线如图2所示。计算工况:俯仰角为90°;方位角在0°~180°范围内变化;频率分别为200,300,400 MHz时,不同探测距离条件下的单站RCS近、远场差值曲线。
从图2中可见,差值曲线随方位角的变化不断起伏,船侧对应的方位角90°处散射曲线差异最大;不同距离对比可见,随着近场探测距离的增大,近远场散射之间的差异逐步减小。
为便于比较舰船散射场的均值,采用以下舰船常用的均值统计方法:去掉0°,90°,180°,270°等几个特征方向±4.5°内的结果,将其余数据由dBsm转化为m2,再进行算术平均值计算。
图3给出了图1中舰船模型在不同探测距离下的散射均值。可以看出,在1 dB的误差容差范围内,较近的探测距离下(例如500 m,即为1/4远场距离),散射均值与远场距离下基本一致。因此,对于舰船类复杂目标,RCS试验时探测天线与舰船目标的间距在一定程度内可以远小于传统的远场距离。
根据分析获得散射均值随距离的变化特点,提出基于成像理论的定量预估均值方法,通过近场散射特性评估,来获得与远场条件下基本一致的均值结果。
由于复杂目标的散射可视为多个散射中心贡献的叠加。实际上,散射中心才是目标散射贡献的主要来源。因此,可以将最大散射中心间距与目标的有效尺寸(非物理尺寸)相关联。在此,首先对满足远场条件的均值定义如下:其均值结果与传统远场距离下均值相差在3 dB以内。
目标的有效尺寸设为D′,预估均值对应的远场距离设为R′。利用一维距离像技术描述目标一维散射中心分布,并以此进行定量预估,步骤如下:获取目标在给定频率的一维距离像,如图4所示;找出散射中心的最大间距D′,D′也即目标的有效尺寸;将D′代入表达式R′≥2D′2/λ。
为了验证提出的定量预估均值方法准确性,使用MLFMM软件对图1的舰船模型进行了一维距离像和近场散射仿真,其结果如图4和5所示。从图5

图2 近远场RCS差值曲线对比Fig.2 Comparison of the near-and far-field RCS difference curves

图3 不同频率和探测距离下的典型均值结果Fig.3 The typical mean values at different frequency and detection distance

图4 自由空间中舰船模型的一维距离像(入射方向为舰艏)Fig.4 The one-dimensional image of ship model in free space(the bow is in the incident direction)

图5 不同探测距离下的典型均值结果Fig.5 The typical mean values at different detection distance
中可以发现,散射中心的最大间距D′约为11 m。根据提出的均值定量预估方法,对应的R′及其近场散射结果如图5所示。其表明了探测距离对应有效尺寸D′的均值散射结果接近于远场的散射结果,且在计算的各频点二者相差小于3 dB。验证了一定偏差范围内,均值预估方法可大幅缩减大型目标散射特性测量距离。
3 结论
文中利用MLFMM软件仿真手段,对舰船模型在自由空间的近、远场散射特性进行了仿真分析。结果表明,一定距离下的近场散射与远场散射均值较为一致。由此提出基于成像理论的定量预估均值方法,通过一维距离像技术得到目标的有效尺寸,进而换算均值预估距离,该探测距离下获得的散射均值与传统远场散射均值误差在3 dB以内。最后,通过仿真结果验证了该方法的准确性。提出的分析方法可为大型目标散射特性测量提供解决途径,即在远小于传统远场距离条件下可对目标散射特性均值进行测量。
[1]LEE S W,WANG H T G.Near-field RCS Computation[M].Appendix in the Manual for NcPTD,1991.
[2] JENG S K.Near-field Scattering by Physical Theory of Diffraction and Shooting and Bouncing Rays[J].IEEE Transactions on Antennas Propagation,1998(4):231—234.
[3]EOU R G,PETERS L.Range Requirements in Radar Crosssection Measurements[J].IEEE Transactions on Antennas Propagation,1965:920—928.
[4]KNOTE F T,Senior T B A.How Far is Far[J].IEEE Transactions on Antennas Propagation,1974:732—734.
[5] RAJEEV B.The Far Field:How Far is Far Enough[J].Applied Microwave&Wireless,1999:58—60.
[6]COIFMAN R,ROKHLIN V,WANDZURA S.The Fast Multi-pole Method for the Wave Equation:A Pedestrian Prescription[J].IEEE Transactions on Antennas Propagation,1993:7—12.
