基于快速群搜索算法的双层球面网壳多目标优化

金晶+李丽娟+刘锋+何嘉年

摘要：提出一种新的群智能算法，即多目标快速群搜索优化（MQGSO）算法，以双层球面网壳为研究对象，进行结构节点最大位移最小化和结构质量最轻化的多目标优化设计，网壳优化后的Pareto前沿分布均匀且范围较广，分别对多目标优化和单目标优化后的结构进行多维地震作用时程响应分析。结果表明：多目标优化得到的结构优于单目标的优化结果，所提出的多目标快速群搜索算法能很好地实现复杂空间结构的多目标优化设计。

关键词：双层球面网壳；多目标优化；快速群搜索算法；时程分析；Pareto前沿

中图分类号：TU318 文献标志码：A

0 引 言

近年来，大跨空间结构在体育馆、航空港、火车站等公共建筑中得到广泛应用，其形式包括网架结构、网壳结构、索结构、膜结构或混合结构等。与单层网壳相比，双层网壳对于大跨度方案更具有优势[1]，有关其抗震性能和稳定性的研究成果已有很多[2-3]。网壳结构属于高次超静定结构，遇到地震作用时，具有很强的随机性，其动力性能和破坏机理与高层结构不同。网壳结构的优化设计一般会由多个目标控制，但是由于其结构的复杂性，这方面的研究非常有限，如对网壳结构的动位移进行的全局和局部优化[4]，对大跨网壳结构进行的模糊优化设计[5]，动力荷载作用下以节点最大动位移和塑性杆件比例进行的优化[6]等。传统的结构优化方法以准则法和数学规划法为主导，利用这类方法进行网壳结构优化设计的效果并不理想。随着智能算法的不断发展，群智能算法得到广泛应用[7-12]，在结构优化设计中也取得了良好的效果[8，12]，其中多目标粒子群算法[9-10]是结构优化领域的研究热点之一。多目标优化存在一组均衡的解集，基于Pareto的最优解[11]，决策者可以根据实际情况从一组Pareto最优解中选择一个或多个解作为最终解。根据Pareto最优解理论与拥挤距离机制，本文中笔者提出了一种适用于结构多目标优化设计的算法，即多目标快速群搜索优化算法（Multi-objective Quick Group Search Optimization，MQGSO），并将其应用于双层网壳结构的多目标优化，以结构质量最轻和节点最小位移为目标，得到了良好的优化结构。

1 网壳结构多目标优化模型

1.1 目标函数

以自重最轻和总动应变能最小为优化目标，建立目标函数：f1（x）作为结构质量的目标函数，f2（x）作为结构节点最大位移最小值的目标函数，即有

式中：W为结构总质量；wi为构件线密度；li为构件长度；s为所有节点的x，y，z三个方向的位移；nt为杆件总数。

1.2 约束条件

1.2.1 结构性能约束

结合现行《钢结构设计规范》（GB 50017—2003）[13]中的要求，本文中考虑了结构构件强度、最大位移、构件整体稳定。双层网壳的所有杆件均为薄壁圆杆，其受力情况分为轴心受压构件和轴心受拉构件，根据薄壁圆钢管在规范中的规定，对其进行如下强度验算。

当杆件为轴心受拉构件时，应力σ为

当杆件为轴心受压构件时，需要考虑压杆稳定计算，即

式中：N′，N分别为轴心拉力和轴心压力；An为杆件净面积；A为构件截面积；f′为钢材抗拉强度设计值；φ为轴心受压构件稳定系数；f为钢材抗压强度设计值。

由《钢结构设计规范》附录C，可得到如下计算公式

当λn=λπfyE≤0.215时

式中：λ为构件长细比，λ=l/i；α1，α2，α3均为系数；因薄壁钢管的截面类型为a类，因此系数α1，α2，α3分别为0.41，0.986，0.152。

在地震作用下，以节点最大位移超过结构跨度的1/50为失效准则[14]，各节点的最大允许位移为跨度的1/400[15]。

1.2.2 种群设置

薄壁钢管结构截面优化需要建立一系列离散的截面，将其存入截面库来选取变量。将网壳结构分成3组杆件，即上弦杆、腹杆和下弦杆，其截面在《结构用无缝钢管》（GB 8162—87）中的379种截面中选取，并且将离散的截面和1组连续整数对应，以达到让算法在连续的整数空间中进行搜索。

为了让优化效率更高，设置合理的截面数量与上下界。X为n维决策变量，X={x1，x2，…，xn}，每个决策变量xi在其最大值xmaxi与最小值xmini范围内变化；同理，每个目标函数yi在其最大值ymaxi与最小值ymini范围内变化，即

1.2.3 适应度函数的修正模型

对于适应度函数的修正模型，由于外点罚函数法的思想普遍应用于工程优化设计中，故借助外点罚函数的思想[16]，提出用以下表达式来约束违反性能约束的粒子，即

式中：r1，r2均为惩罚平衡系数；F（Xi，rt）为第i个粒子的适应度函数；g1（X），g2（X）均为第i个粒子的约束函数；ji为第i个粒子对应的目标函数。2 多目标快速群搜索优化算法

2.1 Pareto最优集的选取

快速群搜索优化（Quick Group Search Optimizer，QGSO）算法[15]在单目标优化中具有良好的收敛速度和收敛精度，特别是对于双层网壳这类计算量大的工程优化设计效果较好，基于QGSO算法的MQGSO算法与QGSO算法的区别在于适应度的比较规则不同，在MQGSO中通过支配与非支配关系来比较个体的适应度，从而得到一个Pareto最优集。在得到的Pareto最优集中通过拥挤距离机制选取某一个体作为发现者，进行迭代计算。在处理完每一次迭代的Pareto最优集后，采用文献[17]中拥挤距离机制来选取Pareto前沿中的一部分值作为精英集。

2.2 算法的迭代过程

发现者的选取既决定算法的前进，也关系到算法能否很好地跳出局部最优并使得Pareto最优集分布均匀，同时还影响到算法的收敛精度和收敛速度。本文中选用拥挤距离机制和禁忌搜索算法混合的方法来选择发现者，为了使得Pareto前沿的分布更加饱满与均匀，在迭代搜索前期，选择拥挤距离为无穷大的个体作为发现者，若精英集中存在拥挤距离不为无穷大的个体，则随机选取一个拥挤距离不为无穷大的个体作为发现者，扩大解的分布范围，防止出现解集过分集中而丢失一些优良解。算法迭代至后期，采用禁忌搜索算法，此方法使发现者可以选择未曾被选择的个体，并使算法转向其他区域进行搜索，从而避免算法进入局部最优，这一点和QGSO算法中游荡者随机产生变异之处。endprint

MQGSO在种群迭代更新过程中，搜索者不仅追随着发现者，同时还结合自身历史最优位置进行更新，这一点正是汲取了群搜索优化（Group Search Optimizer，GSO）算法和粒子群优化（Particle Swarm Optimization，PSO）算法各自的特点，没有GSO算法按3个角度搜索的复杂与繁琐，从而产生了一种收敛精度更高的算法。搜索者进行更新，在每一次迭代临时非支配解集里选取前一次迭代中自身位置良好的解进行更新。3 双层网壳多目标优化设计流程

双层网壳多目标优化设计的流程为：

（1）数据准备：几何参数、材料参数以及算法参数的设置，编制薄壁钢管截面库。

（2）种群初始化：随机生成初始化种群，将薄壁钢管截面库的离散信息与一组映射函数相对应，每一个整数编号对应一组截面参数，即钢管的外径和壁厚。

（3）以控制应力和位移为约束，质量最轻和节点的x，y，z三个方向位移最小为优化目标。

（4）引入惩罚平衡系数调整适应度，采用回飞技术处理越界的粒子，并更新种群。

（5）以达到最大迭代次数作为控制条件，如图1所示，其中，INT为目标迭代次数，r为0～1之间均匀分布的随机数，w3为选择因子，取0.8。

双层网壳结构多目标优化实例分析

4.1 算例模型

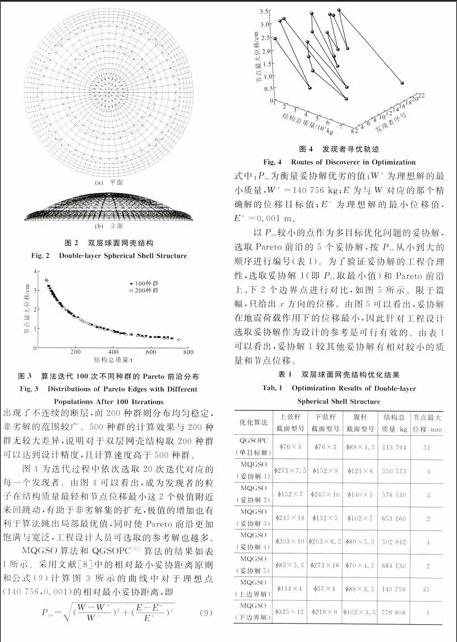
模型选用文献[15]中的网壳结构作为某市场的屋盖，见图2，该算例结构的跨度为83.6 m，矢高为14.0 m，上弦层与下弦层之间的层间高度为1.5 m。网壳使用钢材制造，材料的弹性模量为210 GPa，密度为7 850 kg·m-3，共有6 761个节点，1 834根杆件。上弦层的所有节点均承受5 kN的竖向荷载，节点位移极限为±0.209 m。杆件的允许应力为±215 MPa，压杆和拉杆的最大允许长细比分别为180，300。

4.2 优化结果分析

图3为算法迭代100次不同种群的Pareto前沿分布。由图3可知，200种群的优化结果明显优于100种群的结果，后者不仅前沿分布较窄，同时还

出现了不连续的断层，而200种群则分布均匀稳定，非劣解的范围较广。500种群的计算效果与200种群无较大差异，说明对于双层网壳结构取200种群可以达到设计精度，且计算速度高于500种群。

图4为迭代过程中依次选取20次迭代对应的每一个发现者。由图4可以看出，成为发现者的粒子在结构质量最轻和节点位移最小这2个极值附近来回跳动，有助于非劣解集的扩充，极值的增加也有利于算法跳出局部最优值，同时使Pareto前沿更加饱满与宽泛，工程设计人员可选取的参考解也越多。

算法和QGSOPC[15]算法的结果如表1所示。采用文献[8]中的相对最小妥协距离原则和公式（9）计算图3所示的曲线中对于理想点（140 756，0.001）的相对最小妥协距离，即

式中：Pcs为衡量妥协解优劣的值；W*为理想解的最小质量，W*=140 756 kg；E为与W对应的那个精确解的位移目标值；E*为理想解的最小位移值，E*=0.001 m。

以Pcs较小的点作为多目标优化问题的妥协解，选取Pareto前沿的5个妥协解，按Pcs从小到大的顺序进行编号（表1）。为了验证妥协解的工程合理性，选取妥协解1（即Pcs取最小值）和Pareto前沿上、下2个边界点进行对比，如图5所示。限于篇幅，只给出x方向的位移。由图5可以看出，妥协解在地震荷载作用下的位移最小，因此针对工程设计选取妥协解作为设计的参考是可行有效的。由表1可以看出，妥协解1较其他妥协解有相对较小的质量和节点位移。

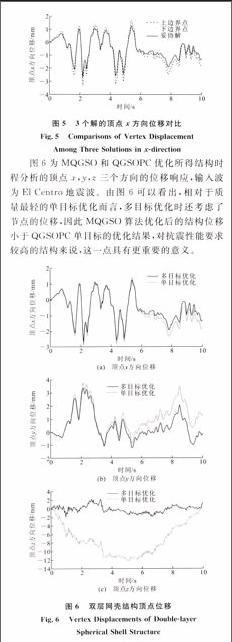
图6为MQGSO和QGSOPC优化所得结构时程分析的顶点x，y，z三个方向的位移响应，输入波为El Centro地震波。由图6可以看出，相对于质量最轻的单目标优化而言，多目标优化时还考虑了节点的位移，因此MQGSO算法优化后的结构位移小于QGSOPC单目标的优化结果，对抗震性能要求较高的结构来说，这一点具有更重要的意义。

图6 双层网壳结构顶点位移

Fig.6 Vertex Displacements of Double-layer

Spherical Shell Structure5 结 语

（1）MQGSO算法在处理带约束的双层网壳多目标优化时具有良好的收敛效果。从优化结果分析可以看出，Pareto前沿分布均匀并且宽泛，曲线过渡平稳无断层，说明MQGSO算法应用于大跨空间结构的多目标优化是可行有效的。

（2）工程设计人员可以根据Pareto前沿选取合适的点作为设计参考值，本文中建议运用相对最小妥协距离求得妥协解进行结构设计。通过妥协解与上下边界点的对比，发现其效果相对更优秀。

（3）多目标优化与单目标优化结果相比，时程分析时的节点位移较小，因为对于结构质量最轻的单目标优化而言，多目标优化时还考虑了节点的位移，这一点与动力性能和抗震优化目标紧密，更适合于抗震设计。

（4）采用x，y，z三个方向位移对其抗震性能的研究具有一定意义，由于震动的随机性，其3个方向均有可能发生破坏，本文中采用时程分析法进行截面校核，如采用此方法对结构进行优化设计则至少按照规范选择3条地震波进行设计。

参考文献：

References：

[1] 何放龙，马自克.强震作用下双层球面网壳结构非线性动力响应分析[J].湖南大学学报：自然科学版，2007，34（10）：1-5.

HE Fang-long，MA Zi-ke.Nonlinear Analysis of Double-layer Reticulated Spherical Dome Under Strong Earthquake Motions[J].Journal of Hunan University：Natural Sciences，2007，34（10）：1-5.endprint

[2]LI L J，XIE Z H，GUO Y C，et al.Structural Optimization and Dynamic Analysis for Double-layer Spherical Reticulated Shell Structures [J].Journal of Constructional Steel Research，2006，62（10）：943-949.

[3]KIM H，QUERIN O M，STEVEN G P.On the Development of Structural Optimisation and Its Relevance in Engineering Design[J].Design Studies，2002，23（1）：85-102.

[4]叶继红，江季松.遗传算法在单层球壳动力响应优化中的应用[J].东南大学学报：自然科学版，2010，40（2）：414-419.

YE Ji-hong，JIANG Ji-song.Application of Genetic Algorithm in Dynamic Response Optimization of Single Layer Dome[J].Journal of Southeast University：Natural Science Edition，2010，40（2）：414-419.

[5]周 臻，孟少平，吴 京.大跨拱支预应力网壳结构的模糊优化设计研究[J].工程力学，2012，29（2）：129-134.

ZHOU Zhen，MENG Shao-ping，WU Jing.Study on Fuzzy Optimization Design for Large-span Arch-suspended Prestressed Reticulated Shells[J].Engineering Mechanics，2012，29（2）：129-134.

[6]刘文政，叶继红.基于遗传-模拟退火算法的单层球面网壳结构破坏模式优化[J].建筑结构学报，2013，34（5）：33-42.

LIU Wen-zheng，YE Ji-hong.Failure Mode Optimization of Single-layer Latticed Spherical Shells with Genetic-simulated Annealing Algorithm[J].Journal of Building Structures，2013，34（5）：33-42.

[7]LI L J，LIU F.Group Search Optimization for Applications in Structural Design[M].Heidelberg：Springer Berlin，2011.

[8]黄冀卓，王 湛.基于遗传算法的抗震钢框架多目标优化设计[J].力学学报，2007，39（3）：389-397.

HUANG Ji-zhuo，WANG Zhan.Multiobjective Optimization Design of Aseismic Steel Frames Using Genetic Algorithm[J].Chinese Journal of Theoretical and Applied Mechanics，2007，39（3）：389-397.

[9]刘衍民，赵庆祯，隋常玲.基于动态多种群的多目标粒子群算法[J].计算机仿真，2011，28（5）：241-245.

LIU Yan-min，ZHAO Qing-zhen，SUI Chang-ling.Multi-objective Particle Swarm Optimizer Based on Dynamic Multi-swarm[J].Computer Simulation，2011，28（5）：241-245.

[10]汪 力，程剑兵，王显强，等.基于多目标粒子群算法的无源电力滤波器优化设计[J].电力系统保护与控制，2011，39（8）：51-55.

WANG Li，CHENG Jian-bing，WANG Xian-qiang，et al.Passive Power Filter Optimal Design Based on Multi-objective PSO Optimization Algorithm[J].Power System Protection and Control，2011，39（8）：51-55.

[11]崔逊学.多目标进化算法及其应用[M].北京：国防工业出版社，2006.

CUI Xun-xue.Multi-objective Evolutionary Algorithms and Their Applications[M].Beijing： National Defense Industry Press，2006.

[12]陈 忠，谢能刚，张子明.结构多目标优化设计的合作博弈解法[J].工程力学，2009，26（4）：32-37.

CHEN Zhong，XIE Neng-gang，ZHANG Zi-ming.Cooperative Game Method for Structural Optimization with Multiple Objectives[J].Engineering Mechanics，2009，26（4）：32-37.

[13]GB 50017—2003，钢结构设计规范[S].

GB 50017—2003，Code for Design of Steel Structures[S].

[14]张 成，吴 慧，高博青.网架结构在地震下的失效模式及其数值表述[J].振动与冲击，2011，30（8）：45-50.

ZHANG Cheng，WU Hui，GAO Bo-qing.Failure Modes and Their Numerical Descriptions of Grid Structures Subjected to Earthquake[M].Journal of Vibration and Shock，2011，30（8）：45-50.

[15]刘 锋，覃 广，李丽娟.快速被动群搜索优化算法及其在空间结构中的应用[J].工程设计学报，2010，17（6）：420-425.

LIU Feng，QIN Guang，Li Li-juan.A Quick Group Search Optimizer with Passive Congregation and Its Application in Spatial Structures[J].Journal of En-gineering Design，2010，17（6）：420-425.

[16]袁亚湘.非线性优化计算方法[M].北京：科学出版社，2008.

YUAN Ya-xiang.Nonlinear Optimization Calculation Method[M].Beijing：Science Press，2008.

[17]DEB K，AGRAWAL S，PRATBA A，et al.A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization：NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197.endprint